3. ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
3.1. Основные понятия статистической проверки гипотезы
Статистическая проверка гипотез тесно связана с теорией оценивания параметров распределений. В экономике, технике, естествознании, медицине, демографии и т.д. часто для выяснения того или иного случайного явления прибегают к высказыванию гипотез (предположений), которые можно проверить статистически, т.е. опираясь на результаты наблюдений в случайной выборке.
Статистической гипотезой называют любое предположение о виде неизвестного закона распределения случайной величины или значении его параметров.
Статистическую гипотезу, однозначно определяющую закон распределения, называют простой, в противном случае ее называют сложной.
Например, статистической является гипотеза о том, что распределение производительности труда рабочих, выполняющих одинаковую работу в одинаковых организационно-технических условиях, имеет нормальный закон распределения, или статистической является также гипотеза о том, что средние размеры деталей, производимых на однотипных, параллельно работающих станках, не различаются между собой.
Основные принципы проверки статистических гипотез состоят в следующем. Пусть f(X,q) - закон распределения случайной величины X, зависящей от одного параметра q. Предположим, что необходимо проверить гипотезу о том, что q = q0, где q0 - определенное число. Назовем эту гипотезу нулевой (проверяемой) и обозначим ее через H0.
Нулевой гипотезой H0 называют выдвинутую гипотезу, которую необходимо проверить.
Конкурирующей (альтернативной) гипотезой H1 называют гипотезу, противоположную нулевой.
Таким образом, задача заключается в проверке гипотезы H0 относительно конкурирующей гипотезы H1 на основании выборки, состоящей из n независимых наблюдений x1, x2, ... , xn над случайной величиной X. Следовательно, все возможное множество выборок объемом n можно разделить на два непересекающихся подмножества (обозначим их через Q и W) таких, что проверяемая гипотеза H0 должна быть отвергнута, если наблюдаемая выборка попадает в подмножество W, и принята если наблюдаемая выборка принадлежит подмножеству Q.
Подмножество W называют критической областью, Q - областью допустимых значений.
Вывод о принадлежности данной выборки к соответствующему подмножеству делают по статистическому критерию.
Статистическим критерием называют однозначно определенное правило, устанавливающее условия, при которых проверяемую гипотезу H0 следует либо отвергнуть либо не отвергнуть.
Основой критерия является специально составленная выборочная характеристика (статистика) Q* = f(x1, x2, ..., xn), точное или приближенное распределение которой известно.
Основные правила проверки гипотезы состоят в том, что если наблюдаемое значение статистики критерия попадает в критическую область, то гипотезу отвергают, если же оно попадает в область допустимых значений, то гипотезу не отвергают (или принимают).
Такой принцип проверки гипотезы не дает логического доказательства или опровержения гипотезы. При использовании этого принципа возможны четыре случая:
- гипотеза H0 верна и ее принимают согласно критерию;
- гипотеза H0 неверна и ее отвергают согласно критерию;
- гипотеза H0 верна но ее отвергают согласно критерию; т.е. допускается ошибка, которую принято называть ошибкой первого рода;
- гипотеза H0 неверна и ее принимают согласно критерию, т.е. допускается ошибка второго рода.
Уровнем значимостиa = 1-g называют вероятность совершить ошибку первого рода, т.е. вероятность отвергнуть нулевую гипотезу H0, когда она верна. С уменьшением a возрастает вероятность ошибки второго рода b.
Мощностью критерия (1 - b) называют вероятность того, что нулевая гипотеза H0 будет отвергнута, если верна конкурирующая гипотеза H1, т.е. вероятность не допустить ошибку второго рода.
Обозначим через P(Q*ÎW½H) вероятность попадания статистики критерия Q* в критическую область W, если верна соответствующая гипотеза H.
Тогда требования к критической области аналитически можно записать следующим образом:
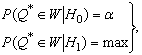 (3.1)
(3.1)
где H0 - нулевая гипотеза;
H1 - конкурирующая гипотеза.
Второе условие выражает требование максимума мощности критерия.
Из условий (3.1) следует, что критическую область нужно выбирать так, чтобы вероятность попадания в нее была бы минимальной (равной a), если верна нулевая гипотеза H0, и максимальной в противоположном случае.
В зависимости от содержания конкурирующей гипотезы H1 выбирают правостороннюю, левостороннюю или двустороннюю критические области.
Границы критической области при заданном уровне значимости a находят из соотношений:
при правосторонней критической области:
P(Q* > Qкр) = a; (3.2)
при левосторонней критической области:
P(Q* < Qкр) = a; (3.3)
при двусторонней критической области:
P(Q* > Qкр.пр.)
= ![]() ; P(Q* < Qкр.лев.)
=
; P(Q* < Qкр.лев.)
= ![]() . (3.4)
. (3.4)
где Qкр.лев. - левосторонняя, а Qкр.пр. - правосторонняя граница критической области.
Следует иметь ввиду, что статистические критерии не доказывают справедливости гипотезы, а лишь устанавливают на принятом уровне значимости ее согласие или несогласие с результатом наблюдений.
При проверке статистических гипотез наряду с известными уже нам законами распределения используется распределение Фишера-Снедекора (F- распределение).