Лемма Маркова. Неравенство и теорема Чебышева.
Теоремы Бернулли и Пуассона

 

Лемма Маркова

 

Пусть Х - случайная величина, принимающая лишь неотрицательные значения. Тогда можно получить следующее неравенство:

 

 (t>0 любое).

Доказательство. Для определенности предположим, что Х - непрерывная случайная величина с плотностью р(х). По определению математического ожидания получаем:

.

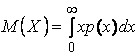Далее будем иметь:

.

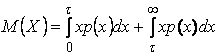Оба слагаемых в правой части не отрицательны, поэтому:

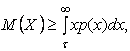
но теперь , и следовательно,

.

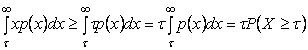Таким образом,

.

Так как >0, получим:

.

 

Рассмотрим теперь случайную величину Х, имеющую математическое ожидание М(Х) и дисперсию D(X). Оценим вероятность события, заключающегося в том, что отклонение Х-М(Х) не превысит по абсолютной величине положительного числа e. Оценка указанной вероятности получается с помощью неравенства Чебышева.

 

Неравенство Чебышева

 

Вероятность того, что отклонение случайной величины Х от ее математического ожидания по абсолютной величине меньше положительного числа e, не меньше, чем , то есть:

.                                                               (1.26)

Доказательство. Приведем доказательство для дискретной (конечной) случайной величины Х:

.

 

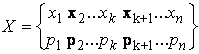Рассмотрим случайную величину . Тогда ее ряд распределения имеет вид:

.

Не ограничивая общность рассуждения, можно предположить, что  первые к значений случайной величины  меньше заданного e, а остальные значения не меньше e. Тогда на основании теоремы сложения вероятностей получим следующую формулу:

.

Чтобы найти , запишем формулу D(X) в виде:

.

 

Опуская в правой части этого равенства первую сумму и заменяя во второй сумме  меньшей величиной e, получим неравенство:

.

 

Из этого неравенства следует:

.                                          (1.28)

Подставляя правую часть (1.28) в (1.26), окончательно получим:

,

что и требовалось доказать.

Рассмотрим достаточно большое число n независимых случайных величин Х₁, Х₂, … Х_n. Если дисперсии их ограничены числом с, то событие, заключающееся в том, что отклонение среднего арифметического этих случайных величин от среднего арифметического их математических ожиданий будет по абсолютной величине сколь угодно малым, является почти достоверным. Это предложение, относящиеся к закону больших чисел, доказал П.Л. Чебышев.

 

Теорема Чебышева. Если Х₁, Х₂, … Х_n попарно независимые случайные величины, причем  дисперсии их не превышают постоянно числа с, то как бы мало ни было положительное число e, вероятность неравенства:

будет как угодно близка к единице, если число n случайных величин достаточно велико.

Используя понятие предела, можно в условиях теоремы записать:

.

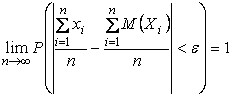Вместо последней записи часто кратко говорят, что суммы  сходятся по вероятности к нулю.

Доказательство. Рассмотрим случайную величину 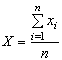. На основании свойств математического ожидания и дисперсии можно записать:

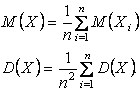
По условию теоремы D(X_i)c, поэтому .

 

Теперь можно воспользоваться неравенством Чебышева:

.

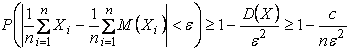Переходя к пределу при , будем иметь:

.

 

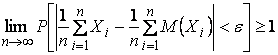Так как вероятность не  может быть больше единицы, этот предел равен единице, что и требовалось доказать.

 

Из теоремы Чебышева следует утверждение, заключающееся в том, что среднее арифметическое достаточно большого числа независимых случайных величин, имеющих ограниченные дисперсии, утрачивает случайный характер и становится детерминированной величиной.

 

Пример 1.19. Дисперсия каждой из 6250 независимых случайных величин не превосходит 9. Оценить вероятность того, что абсолютная величина отклонения средней арифметической этих случайных величин от средней арифметической их математических ожиданий не превысит 0,6.

Решение. Согласно теореме Чебышева искомая вероятность Р не меньше 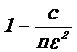. По условиям задачи с=9, n=6250, e=0,6, следовательно, Р³0,996.

Отметим некоторые важные частные случаи теоремы Чебышева.

Теорема Бернулли. Пусть производится n независимых испытаний, в каждом из которых вероятность появления события постоянна и равна р. Тогда каково бы ни было e>0:

,

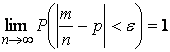где  - частость появления события А.

 

Доказательство. Для доказательства рассмотрим случайную величину Х_i=m_i, являющуюся числом наступления события А в I испытании, так что m=m₁+m₂+…+m_i+…+m_n, и случайные величины m_i попарно независимы. Ранее было показано, что М(m_i)=p и D(m_i)=pq. Так как , то дисперсии случайных величин m_i ограничены одним и тем же числом , следовательно, получаем все условия, при которых справедлива теорема Чебышева и окончательно получим:

,

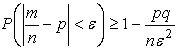откуда:

.

 

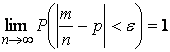Пример 1.20. На предприятии, выпускающем кинескопы, 0,8 всей продукции выдерживает гарантийный срок службы. С вероятностью, превышающей 0,95, найти пределы, в которых  находится доля кинескопов, выдерживающих гарантийный срок, из партии 8000 кинескопов.

Решение. Применяем теорему Бернулли при n=8000, Р³0,95, р=0,8 и q=0,2. Подставляя в равенство:

p,q и n, найдем e=0,02. Из неравенства получим .

 

Теорема Пуассона. Если в последовательности независимых испытаний появление события А в k-ом испытании равна р_к, то:

,

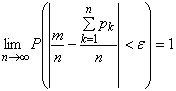где m есть случайная величина, равная числу появлений события А в первых n испытаниях.

Доказательство. Пусть случайная величина Х_к=m_k означает число появления события А в k-м испытании. Тогда , и случайные величины m_k попарно независимы. Таким образом, теорема Пуассона является частным случаем теоремы Чебышева. На основании свойств математического ожидания и дисперсии случайной величины  получим следующие формулы:

        

Подставляя эти формулы в неравенство Чебышева, получаем неравенство, выражающее теорему Пуассона:

.

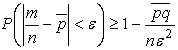Пример 1.21. Произведено 900 независимых испытаний, причем в 450 из этих испытаний вероятность появления события А равна 2/3, в 200 - 0,5, в 160 - 0,3 и в 90 - 0,4. Найти оценку вероятности того, что частость появления события А отклоняется по абсолютной величине от средней вероятности не больше, чем на 0,1.

Решение. Применяем теорему Пуассона. Находим :

,

.

 

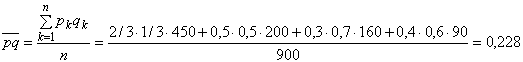Подставляя в правую часть неравенства:

значения , e и n, получим Р³0,97.

Теорема Бернулли является частным случаем теоремы Пуассона.

В самом деле, если вероятность появления данного события в каждом испытании постоянна: р₁=р₂=…р_n=р, то  и .

Замечание. В тех случаях, когда вероятность появления события в каждом испытании не известна, за верхнюю границу дисперсии принимают с=1/4, т.е.:

.

 

Теорема Лапласа

 

Теоремы Чебышева, Бернулли, Пуассона устанавливают нижнюю границу вероятности, что часто бывает недостаточно. В некоторых случаях важно знать достаточно точное значение вероятности. Этому требованию отвечают так называемые предельные теоремы закона больших чисел, указывающие асимптотические формулы для вероятностей неравенства  относительно n случайных величин X_i.

Мы уже знаем, что вероятность неравенства  вычисляется по интегральной теорема  Лапласа, а именно:

,

где .

Следовательно, достаточно точным выражением теоремы Бернулли является интегральная теорема Лапласа. Асимптотическую формулу для теоремы Чебышева доказал его ученик А.М. Ляпунов. Приведем теорему Ляпунова без доказательства.

 

 

К оглавлению

Назад к разделу "Закон  больших чисел"

Вперед к разделу "Центральная предельная теорема"