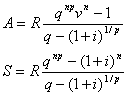1.8 Анализ переменных потоков платежей
Временные интервалы между последовательными платежами в нерегулярном потоке могут быть любыми, не постоянными, любыми могут быть так же и члены потока. Обобщающие характеристики в этом случае получают только путем прямого счета:
наращенная
сумма 
,
современная
величина 
,
где t- время от начала потока платежей до момента выплаты, Rt – сумма платежа.
Переменная рента с разовыми изменениями размеров платежа
Пусть общая продолжительность ренты n и этот срок разбит на k участков продолжительностью n1, n2, … , nk, в каждом из которых член ренты постоянен и равен Rt, t=1, 2, …, k, но изменяется от участка к участку.
Тогда наращенная сумма для годовой ренты постнумерандо (p=1, m=1) вычисляется по формуле
а современная величина как
.
Рента с постоянным абсолютным приростом платежей
Пусть размер платежей изменяется с постоянным приростом a (положительным или отрицательным). Если рента годовая постнумерандо, то размеры последовательных платежей составят R, R+a, R+2a,…, R+(n-1)a. Величина t-го члена равна Rt=R+(t-1)a.
Тогда современная стоимость такой ренты равна
,
а наращенная сумма
.
В
случае p-срочной ренты с постоянным
приростом платежей (m=1)
последовательные выплаты равны 
, где a
– прирост платежей за год, R – первый платеж,
то есть
, где t – номер члена
ряда, t=1, 2, … , np.
Современная величина
,
а наращенная сумма
.
Ренты с постоянным относительным изменением платежей
Если платежи годовой ренты изменяются с постоянным темпом роста q, то члены ренты будут представлять собой ряд: R, Rq, … , Rqn-1. Величина t-го члена равна Rt=Rqt-1.
Для того чтобы получить современную величину, дисконтируем эти величины:
Rv, Rqv2,.., Rqn-1vn. Мы получили геометрическую прогрессию.
Сумма этих величин равна
.
Наращенная сумма
.
Для p-срочной ренты (m=1):
