1.6 Определение параметров финансовой ренты

 

 

Иногда при разработке контрактов возникает задача определения по заданной наращенной сумме ренты S или ее современной стоимости A остальных параметров ренты: R, n, i, p, m. Такие параметры как m и pобычно задаются по согласию двух подписывающих сторон. Остаются параметры R, n, i. Два из них задаются, а третий рассчитывается. Такие расчеты могут быть неоднократно повторены при различных значениях задаваемых параметров, пока не будет достигнуто согласие сторон.

 

Определение размера ежегодной суммы платежа R

 

В зависимости от того какая обобщающая характеристика постоянной ренты задана S или A, возможны два варианта расчета

 

R=S/s_n;i                                                               (1.15)

или

R=A/a_n;i.                                                             (1.16)

 

Определение срока постоянной ренты

 

Рассмотрим решение этой задачи на примере обычной годовой ренты с постоянными заданными платежами. Решая исходные формулы для S и A

 

                           и         

 

относительно срока n, получаем соответственно следующие два выражения

 

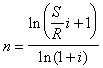                 и  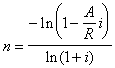        (1.17)

Последнее выражение, очевидно, имеет смысл только при R>Ai.

 

Определение ставки процентов

 

 

Для того, чтобы найти ставку i, необходимо решить одно из нелинейных уравнений (опять предполагаем, что речь идет о постоянной годовой ренте постнумерандо) следующего вида

      или    ,

которые эквивалентны двум другим

                  

         или             (1.18)

В этих уравнениях единственным неизвестным является процентная ставка i. Решение нелинейных уравнений может быть найдено лишь приближенно. Известно несколько методов решения таких уравнений: метод линейной интерполяции, метод Ньютона-Рафсона и др. Мы рассмотрим сначала первый из них.

 

Метод линейной интерполяции

 

         Прежде всего нужно найти с помощью прикидочных расчетов нижнюю (i_н) и верхнюю (i_в) оценки ставки. Это осуществляется путем подстановки в одну из формул (1.18) различных числовых значенийi и сравнения результата с правой частью выражения.         Далее корректировка нижнего значения ставки производится по следующей интерполяционной формуле

         ,                                             (1.19)

в которой s_в и s_в - значения коэффициента наращения (или коэффициента приведения) ренты для процентных ставок i_н и i_в соответственно. Полученное значение ставки проверяют, подставляя его в левую часть исходного уравнения и сравнивая результат с правой частью. Если достигнутая точность недостаточна, повторно применяют формулу (1.19), заменив в ней значение одной из приближенных оценок ставки на более точное, найденное на предыдущей итерации, и соответствующее ей значение множителя наращения (или приведения).

 

Метод Ньютона-Рафсона

 

         В этом методе решение также находят итеративно, постепенно шаг за шагом уточняя оценку. Метод разработан для решения нелинейных уравнений вида

f(x)=0.

         В нашем конкретном случае алгоритм поиска сводится к трем операциям на каждом шаге, которые зависят от постановки задачи (задана  S или A) и типа ренты.

         Сначала будем считать, что известна наращенная сумма S и найдена какая-то начальная оценка процентной ставки (например, методом проб).

А) Постоянная годовая рента постнумерандо, проценты начисляются один раз в конце года, p=1, m=1.

Требуется решить уравнение вида

   или  

Если ввести обозначение q=1+i и умножить обе части уравнения на –(q-1), то получим  алгоритм уточнения оценки на каждом шаге k, состоящий из следующих трех операций:

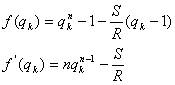
Б)  Постоянная p-срочная рента постнумерандо, проценты начисляются один раз в конце года, p³1, m=1.

Требуется решить уравнение вида

   или   .

 

Вновь используем обозначение q=1+i  и получим алгоритм уточнения оценки на каждом шаге k, состоящий из следующих трех операций:

Замечания:

1)     Начальную оценку q₀=1+i₀, требующуюся для начала итеративной процедуры следует выбирать такой, чтобы соответствующий ей множитель  наращения был как можно ближе к заданному отношению S/R. Это сократит число итераций и обеспечит сходимость алгоритма.

2)     Остановка вычислений осуществляется после того как проверка, заключающаяся в сравнении множителя наращения и отношения S/R, свидетельствует об их совпадении с достаточной (наперед заданной) точностью.

        

Теперь будем считать, что известна современная стоимость A и найдена какая-то подходящая начальная оценка процентной ставки.

А) Постоянная годовая рента постнумерандо, проценты начисляются один раз в конце года, p=1, m=1.

Требуется решить уравнение вида

 или 

Здесь также используем обозначение q=1+i, и после умножения обеих частей равенства на (q-1) получим алгоритм уточнения оценки на каждом шаге k, состоящий из следующих трех операций:

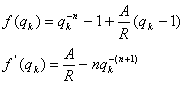
Б)  Постоянная p-срочная рента постнумерандо, проценты начисляются один раз в конце года, p³1, m=1.

Требуется решить уравнение вида

    или   ..

 

 

 

Сделав подстановку q=1+i, получим алгоритм уточнения оценки на каждом шаге k, состоящий из следующих трех операций:

.

 

 

К оглавлению

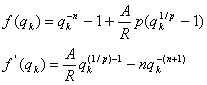
Назад к разделу "1.5 Зависимость между современной величиной  и наращенной суммой ренты"

Вперед к разделу "1.7 Другие виды постоянных рент"