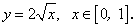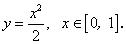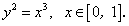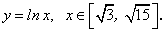Сегодня вы изучите вопросы
-
Вычисление площадей плоских фигур
-
Вычисление объема тел по площадям перпендикулярных сечений
-
Вычисление длины дуги плоской кривой
-
Вычисление площади поверхности вращения
-
Вычисление работы переменной силы
Изучив тему занятия, вы сможете
-
найти площадь плоской фигуры;
-
найти объем тела;
-
найти величину работы переменной силы;
-
вычислить длину дуги;
-
вычислить площадь поверхности вращения;
Основные понятия
Вычислить площадь плоской фигуры, ограниченной сверху линией 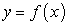 , снизу линией
, снизу линией 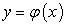 , слева и справа прямыми
, слева и справа прямыми 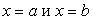 соответственно (рис. 5.4
соответственно (рис. 5.4 ).
).
Решение поставленной задачи сводится к вычислению площади заштрихованной фигуры на рисунке 5.4. Очевидно, эта площадь равна разности площадей 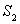 и
и 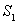 двух криволинейных трапеций
двух криволинейных трапеций 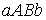 и
и 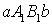 , каждая из которых вычисляется по известной формуле:
, каждая из которых вычисляется по известной формуле:
Поэтому искомая площадь равна разности этих интегралов:
По аналогии, для вычисления площади плоской фигуры, ограниченной справа линией 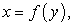 слева линией
слева линией 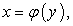 снизу прямой
снизу прямой 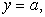 сверху прямой
сверху прямой 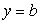 (рис. 5.5
(рис. 5.5 ), получим:
), получим:
Пример 1. Требуется найти площадь плоской фигуры, ограниченной линиями: 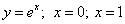 ;
; 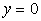 .
.
Решение. Строим графики заданных линий (рис. 5.6 ). Искомая площадь
). Искомая площадь 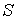 равна площади криволинейной трапеции ОАВС, которая по определению (занятие 12) равна определенному интегралу
равна площади криволинейной трапеции ОАВС, которая по определению (занятие 12) равна определенному интегралу 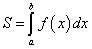 .
.
Отсюда находим:
Пример 2. Требуется найти площадь фигуры, ограниченной линиями:
Решение. Строим графики заданных линий (рис. 5.7 ).
).
По формуле (219) искомая площадь равна:
Пример 3. Вычислить площадь плоской фигуры, ограниченной линиями: 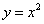 ,
, 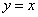 .
.
Решение. Строим графики функций 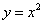 ,
, 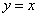 (рис. 5.8
(рис. 5.8 ).
).
Найдем абсциссы точек пересечения линий 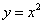 и
и 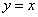 . Для этого необходимо решить систему уравнений:
. Для этого необходимо решить систему уравнений: 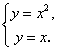
Имеем:
Искомая площадь равна площади заштрихованной плоской фигуры (рис. 5.8).
По формуле (219) искомая площадь равна:
Здесь 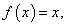
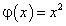 ; слева и справа искомая фигура ограничена соответственно прямыми
; слева и справа искомая фигура ограничена соответственно прямыми 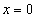 и
и 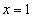 .
.
Отсюда находим:
Пример 4. Вычислить площадь плоской фигуры, ограниченной эллипсом (рис. 5.9 ):
):
Решение. Построим график функции, заданной уравнением (220). Найдем точки пересечения эллипса с осями координат: при 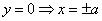 ; при
; при 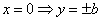 .
.
Уравнение эллипса задается функциями:
В силу симметрии эллипса относительно осей координат достаточно найти площадь ее четвертой (заштрихованной) части.
Имеем:
Таким образом, площадь эллипса равна:
Пример 5. Найти площадь плоской фигуры, ограниченной линиями 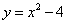 , у = 0.
, у = 0.
Решение. Находим точки пересечения параболы 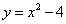 с осями координат:
с осями координат:
Вершина параболы 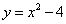 лежит на оси
лежит на оси 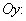 В (0; –4) (рис. 5.10
В (0; –4) (рис. 5.10 ).
).
Искомая площадь — площадь фигуры АВС, заштрихованная на рисунке, сверху ограничена прямой 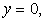 снизу линией
снизу линией 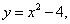 слева прямой
слева прямой 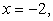 справа прямой
справа прямой 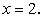
Отсюда по формуле (219) имеем:
Пусть замкнутое тело Т (рис. 5.11 ) ограничено слева плоскостью
) ограничено слева плоскостью 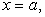 , справа —
, справа — 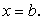 Пусть для любого значения
Пусть для любого значения 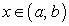 задается площадь
задается площадь 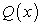 сечения, перпендикулярного оси Ох. Требуется найти объем V тела Т.
сечения, перпендикулярного оси Ох. Требуется найти объем V тела Т.
Отыскание объема V тела проведем по вышеизложенной схеме построения интегральной суммы. Разобьем отрезок [a; b] точками 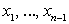 на n произвольных частей. В каждой части возьмем по произвольной точке
на n произвольных частей. В каждой части возьмем по произвольной точке 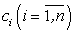 ; найдем площадь
; найдем площадь 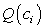 перпендикулярного сечения. Объем
перпендикулярного сечения. Объем 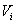 части
части 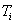 тела Т, ограниченного плоскостями
тела Т, ограниченного плоскостями 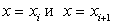 , приближенно заменим объемом цилиндра с площадью основания
, приближенно заменим объемом цилиндра с площадью основания 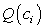 и высотой
и высотой 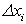 . Аналогично поступая со всеми частями тела Т, получим:
. Аналогично поступая со всеми частями тела Т, получим:
Точное выражение объема V тела Т получим предельным переходом в равенстве (222) при 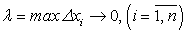 :
:
По определению определенного интеграла равенство (223) переписывается так:
Рассмотрим частный случай, когда тело Т получено вращением криволинейной трапеции 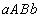 вокруг оси
вокруг оси 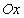 (рис. 5.12
(рис. 5.12 ).
).
В этом частном случае площадь перпендикулярного сечения равна площади круга, радиус которого равен ординате линии 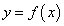 :
:
По формуле (224) имеем:
Пример 6. Вычислить объем трехосного эллипсоида (рис. 5.13 ).
).
Фиксируем х в уравнении (226). Найдем уравнение полученной линии:
Уравнение (227) в плоскости декартовых координат 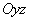 является уравнением эллипса, площадь которого по формуле (221) равна произведению
является уравнением эллипса, площадь которого по формуле (221) равна произведению  на длины полуосей эллипса (227):
на длины полуосей эллипса (227):
Следовательно, площадь Q(х) перпендикулярного к оси Ох сечения равна:
Так как объем V тела по площадям Q(x) перпендикулярного к оси Ох сечения определяется по формуле 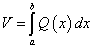 , то с учетом симметрии трехосного эллипсоида получим:
, то с учетом симметрии трехосного эллипсоида получим:
Отсюда, в частности, легко найти объем шара, для которого 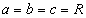 :
:
Пример 7. Вычислить объем тела, образованного вращением плоской фигуры, ограниченной линиями 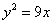 и у = 3х, вокруг оси
и у = 3х, вокруг оси 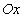 .
.
Решение. Строим графики линий 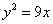 и у = 3х (рис. 5.14
и у = 3х (рис. 5.14 ); находим абсциссы их точек пересечения, решив систему уравнений:
); находим абсциссы их точек пересечения, решив систему уравнений:
Искомый объем равен разности двух объемов: от вращения фигуры, ограниченной параболой 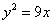 , прямой х = 1 и осью Ох, и фигуры, ограниченной прямыми у = 3х, х = 1, у = 0 вокруг оси
, прямой х = 1 и осью Ох, и фигуры, ограниченной прямыми у = 3х, х = 1, у = 0 вокруг оси 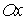 .
.
Как известно, объем тела вращения вокруг оси Ох определяется по формуле:
Отсюда находим, что искомый объем равен:
В декартовой системе координат Оху дана линия своим уравнением 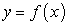 .
.
Пусть 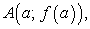
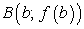 — фиксированные точки линии
— фиксированные точки линии 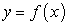 . Требуется найти длину линии от точки А до точки В (рис. 5.15
. Требуется найти длину линии от точки А до точки В (рис. 5.15 ).
).
За величину длины дуги незамкнутой плоской кривой принимается предел длины ломаной, вписанной в эту дугу, при стремлении к нулю наибольшего звена.
незамкнутой плоской кривой принимается предел длины ломаной, вписанной в эту дугу, при стремлении к нулю наибольшего звена.
Длину искомой дуги (так будем называть часть линии 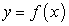 от точки А до точки В) найдем по известной схеме построения определенного интеграла.
от точки А до точки В) найдем по известной схеме построения определенного интеграла.
Разделим отрезок [a; b] точками 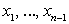 на n произвольных частей. Через точки деления отрезка [a; b] проведем прямые, параллельные оси Оу. Этими прямыми дуга AB разделится на n частей:
на n произвольных частей. Через точки деления отрезка [a; b] проведем прямые, параллельные оси Оу. Этими прямыми дуга AB разделится на n частей: 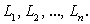
Возьмем i-ую часть 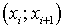 отрезка [a; b]. Внутри i-ой части возьмем произвольную точку
отрезка [a; b]. Внутри i-ой части возьмем произвольную точку 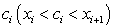 . Приближенно заменим длину
. Приближенно заменим длину 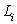 дуги
дуги 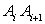 отрезком длины касательной, проведенной в точке
отрезком длины касательной, проведенной в точке 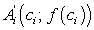 , ограниченной прямыми
, ограниченной прямыми 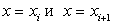 .
.
Уравнением касательной в точке 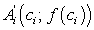 является
является
При 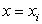 ордината касательной равна:
ордината касательной равна:
Длину касательной, заключенной между прямыми 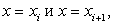 найдем по координатам найденных точек
найдем по координатам найденных точек 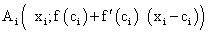 ,
, 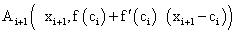 .
.
Аналогично поступим со всеми частями дуги 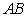 ; исходя из этих предположений, будем иметь:
; исходя из этих предположений, будем иметь:
Пусть 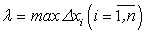 . Переходя к пределу в приближенном равенстве (230) при
. Переходя к пределу в приближенном равенстве (230) при 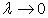 , получим интегральную сумму:
, получим интегральную сумму:
По определению определенного интеграла имеем:
Остается доказать, что длина ломаной i-го звена и длина касательной на i-ом участке являются эквивалентными б.м.в. при 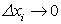 .
.
Обозначим через li длину ломаной i-го звена.
Имеем:
Пример 8. Вычислить длину дуги параболы 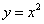 , ограниченной прямыми х = 0 и
, ограниченной прямыми х = 0 и 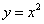 (рис. 5.16
(рис. 5.16 ).
).
Решение. Длина дуги ОА параболы, по доказанному, определяется по формуле 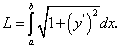 Здесь а = 0;
Здесь а = 0; 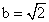 ;
; 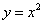 . Найдем выражение подынтегральной функции:
. Найдем выражение подынтегральной функции:
Отсюда следует, что искомая длина дуги равна интегралу 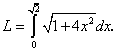
Для вычисления последнего интеграла воспользуемся табличным интегралом
Отсюда находим:
В прямоугольной системе координат Оху дана гладкая линия своим уравнением 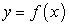 , ограниченная прямыми
, ограниченная прямыми 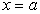 и
и 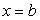 . Требуется найти площадь P поверхности, полученной от вращения дуги АВ вокруг оси
. Требуется найти площадь P поверхности, полученной от вращения дуги АВ вокруг оси 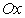 (рис. 5.17
(рис. 5.17 ).
).
По аналогии с предыдущими задачами, разобьем отрезок [a; b] на n произвольных частей точками 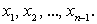
Через точки деления проведем плоскости, перпендикулярные оси Ох.
Этими плоскостями искомая площадь P разделится на n частей 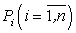 .
.
Найдем приближенное выражение для 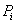 .
.
На отрезке 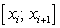 возьмем произвольную точку
возьмем произвольную точку 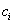 . Найдем ординату
. Найдем ординату 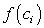 точки
точки 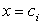 линии
линии 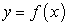 . Через точку
. Через точку 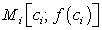 проведем касательную
проведем касательную 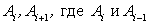 — точки пересечения касательной с прямыми
— точки пересечения касательной с прямыми 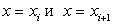 .
.
При вращении отрезка 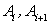 вокруг оси
вокруг оси 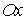 получим боковую поверхность усеченного конуса. Сделаем приближенную замену:
получим боковую поверхность усеченного конуса. Сделаем приближенную замену:
Найдем элементы равенства (233).
С помощью равенства (234) находим искомые ординаты касательной:
Длину отрезка 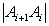 найдем по формуле
найдем по формуле 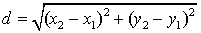 :
:
Из равенств (233) — (236) следует, что
Поступая аналогично со всеми частями поверхности вращения, получим:
Из равенства (238) следует, что при 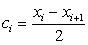 (т.е. если за ci взять середину отрезка [
(т.е. если за ci взять середину отрезка [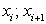 ]) слагаемое
]) слагаемое 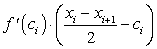 суммы (238) будет равно нулю.
суммы (238) будет равно нулю.
Если обозначить через 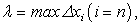 где
где 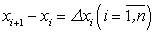 , и перейти к пределу при
, и перейти к пределу при 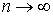 , то получим
, то получим 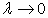
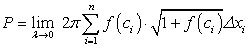 , что представляет интегральную сумму функции
, что представляет интегральную сумму функции 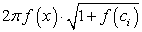 .
.
Окончательно находим, что:
Пример 9. Вычислить площадь поверхности, образованной вращением части линии 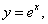 ограниченной прямыми х = 0 и х = 1, вокруг оси Ох (рис. 5.18
ограниченной прямыми х = 0 и х = 1, вокруг оси Ох (рис. 5.18 ).
).
Решение. Найдем выражение подынтегральной функции:
Площадь поверхности вращения найдем по формуле (239):
найдем по формуле (239):
Предварительно найдем ее компоненты. По условиям задачи:
Отсюда находим:
Пример 10. Тело Т под действием переменной силы F, действующей в направлении оси Ох, переместилось из точки х = 3 м в точку х = 5 м. Найти работу этой силы, если известен закон изменения величины силы при перемещении тела вдоль оси Ох: F = 5х (н).
Решение. Нам известно, что в безразмерных величинах 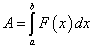 .
.
Отсюда находим, что искомая работа равна:
Пример 11. Какую работу нужно затратить, чтобы растянуть пружину на 5 см, если сила в 100 н растягивает пружину на 1 см?
Решение. Согласно закону Гука, величина упругой силы, действующей на пружину, возрастает пропорционально растяжению пружины. Если за х принять длину растяжения, а за 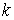 принять коэффициент пропорциональности, то величина упругой силы
принять коэффициент пропорциональности, то величина упругой силы определяется по формуле: F = k ∙ x.
определяется по формуле: F = k ∙ x.
Найдем коэффициент пропорциональности 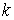 из заданных условий задачи:
из заданных условий задачи:
Искомая работа вычисляется по формуле: 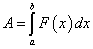 .
.
Здесь по условиям задачи: а = 0, b = 0,05 м, 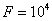 н/м.
н/м.
Имеем:
Контрольные вопросы
-
Как с помощью определенного интеграла вычисляются площади плоских фигур?
-
Как с помощью определенного интеграла вычисляются объемы по площадям перпендикулярных сечений, объемы тел вращения?
-
Как с помощью определенного интеграла вычисляется длина плоской дуги, работа переменной силы?
-
Выведите формулу работы переменной силы.
-
Придумайте задачу физического или экономического содержания, которая приводит к необходимости вычисления определенного интеграла.
Задания для самостоятельной работы
-
Вычислите площадь фигуры, ограниченной линиями:
-
Вычислите объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной линиями:
-
Найдите длины дуг следующих линий:
-
Скорость движения точки задана равенством
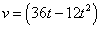 м/с.
м/с.Найдите путь, пройденный точкой от начала движения до ее остановки.
-
Вычислите силу давления воды на вертикальную заслонку, закрывающую трубу, если труба, лежащая горизонтально, наполовину заполнена водой. Известно, что поперечным сечением трубы является круг диаметром 6 м.
-
Вычислите работу, которую надо затратить на сжатие пружины на 0.1 м, если для сжатия ее на 0.01 м нужна сила в 78 н.
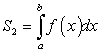 и
и 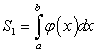 .
.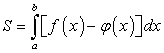 . (219)
. (219)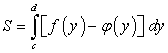 .
.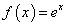 ;
; 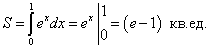
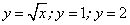 ;
; 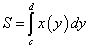 , где
, где 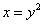 ,
, 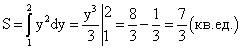 .
.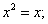
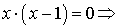
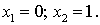
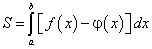 .
.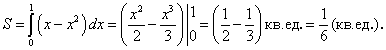
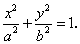 (220)
(220)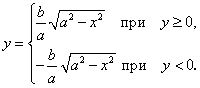
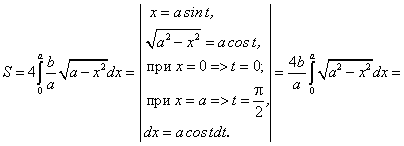
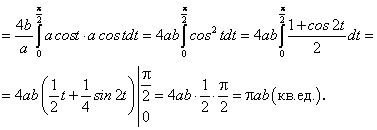
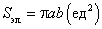 (221)
(221)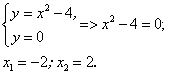
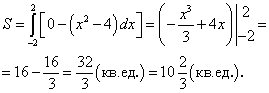
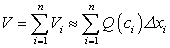 . (222)
. (222)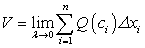 . (223)
. (223)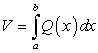 . (224)
. (224)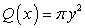 .
.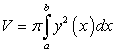 . (225)
. (225)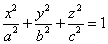 . (226)
. (226)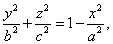 или
или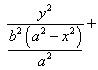
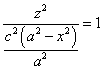 (227)
(227)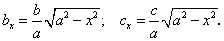
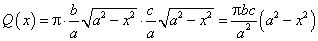 .
.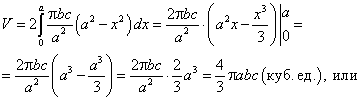
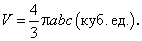 (228)
(228)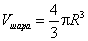 . (229)
. (229)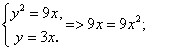

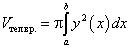 .
.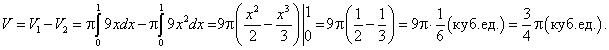
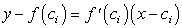 .
.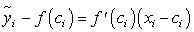 .
.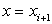 имеем:
имеем: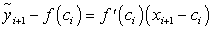 .
.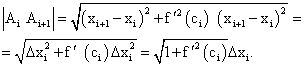
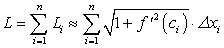 . (230)
. (230)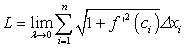 . (231)
. (231)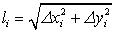 ;
; 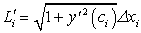 ;
;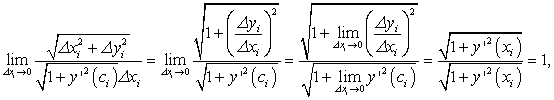
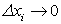 точка
точка 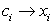 .
.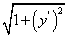 =
= 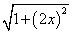 =
= 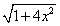 .
.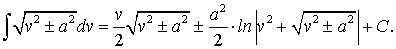
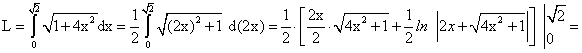
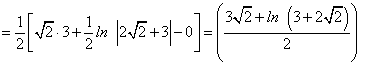 (ед.).
(ед.).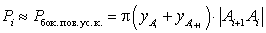 . (233)
. (233)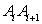 таково:
таково: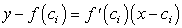 . (234)
. (234)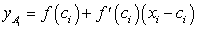 ,
,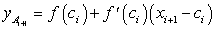 . (235)
. (235)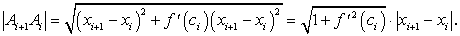 (236)
(236)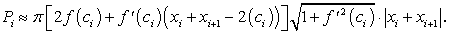 (237)
(237)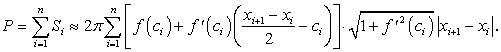 (238)
(238)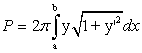 . (239)
. (239)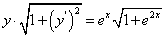 .
.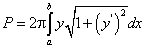 .
.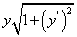 =
= 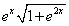 .
.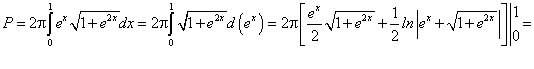
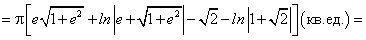
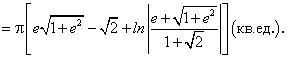
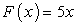 .
.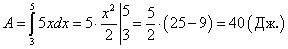 .
.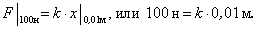
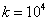 н/м.
н/м.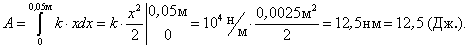
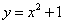 ,
, 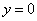 ,
, 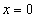 ,
, 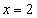 .
.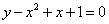 ,
, 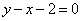 .
.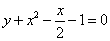 ,
, 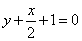
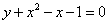 ,
, 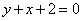 .
.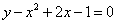 ,
, 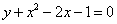 .
.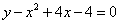 ,
, 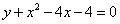 .
.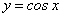 ,
, 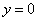 ,
, 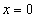 ,
, 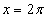 .
.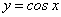 ,
, 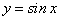 ,
, 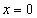 ,
, 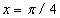 .
.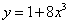 ,
, 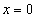 ,
, 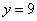 .
.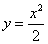 ,
, 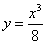 .
.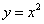 ,
, 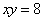 ,
, 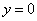 ,
, 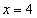 .
.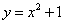 ,
, 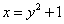 ,
, 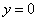 ,
, 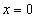 ,
, 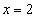 .
.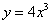 ,
, 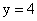 ,
, 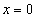 .
.