Сегодня вы изучите вопросы
-
Определенный интеграл. Задачи, приводящие к понятию определенного интеграла
-
Основные свойства определенного интеграла
-
Производная определенного интеграла по переменному верхнему пределу
-
Вычисление определенного интеграла. Формула Ньютона–Лейбница
-
Свойство аддитивности определенного интеграла по промежутку интегрирования
-
Вычисление определенных интегралов путем замены переменной
-
Интегрирование по частям определенного интеграла
Изучив тему занятия, вы сможете
-
вычислять определенные интегралы;
-
выражать неопределенные интегралы через определенные.
Основные понятия
-
определенный интеграл с постоянными пределами интеграции,
-
определенный интеграл с переменными пределами интеграции.
Задача о вычислении площади криволинейной трапеции
В системе декартовых координат Оху дана криволинейная трапеция, ограниченная сверху линией 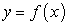 , снизу осью Ох, справа и слева соответственно прямыми
, снизу осью Ох, справа и слева соответственно прямыми 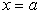 и
и 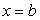 (рис. 5.1
(рис. 5.1 ).
).
Разделим отрезок 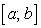 на n произвольных частей точками
на n произвольных частей точками 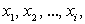
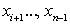 . Через точки деления проведем прямые, параллельные оси OY. Этими прямыми криволинейная трапеция аbВА разделится на n произвольных частей. Обозначим через S площадь криволинейной трапеции, а через
. Через точки деления проведем прямые, параллельные оси OY. Этими прямыми криволинейная трапеция аbВА разделится на n произвольных частей. Обозначим через S площадь криволинейной трапеции, а через 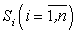 площади полученных ее частей при таком разбиении.
площади полученных ее частей при таком разбиении.
Рассмотрим i-ую часть криволинейной трапеции, ограниченную прямыми 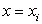 и
и 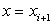 Возьмем внутри отрезка
Возьмем внутри отрезка  произвольную точку
произвольную точку 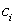 . Найдем значение функции
. Найдем значение функции 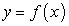 в этой точке:
в этой точке:  . Приближенно площадь
. Приближенно площадь 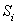 i-ой части криволинейной трапеции заменим площадью прямоугольника с основанием
i-ой части криволинейной трапеции заменим площадью прямоугольника с основанием 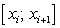 и высотой
и высотой 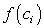 .
.
Приближенное выражение 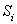 i-ой площади выглядит так:
i-ой площади выглядит так:
Аналогично поступив со всеми частями площади криволинейной трапеции, получим:
Очевидно, чем меньше по величине 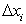
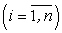 , тем точнее приближенное равенство (193). Так как отрезок [a; b] делится нами произвольным образом на n частей, то стремление числа делений к бесконечности еще не обеспечивает стремление к нулю всех
, тем точнее приближенное равенство (193). Так как отрезок [a; b] делится нами произвольным образом на n частей, то стремление числа делений к бесконечности еще не обеспечивает стремление к нулю всех 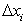
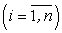 одновременно. Это связано с тем, что мы можем, в частности, делить до бесконечности всего один отрезок, а остальные отрезки оставить без изменения.
одновременно. Это связано с тем, что мы можем, в частности, делить до бесконечности всего один отрезок, а остальные отрезки оставить без изменения.
Поэтому для обеспечения стремления к нулю всех без исключения отрезков 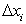
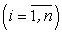 вводят величину
вводят величину 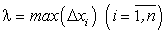 и переходят к пределу в равенстве (193) при
и переходят к пределу в равенстве (193) при 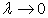 .
.
Очевидно, если 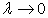 , то все без исключения отрезки
, то все без исключения отрезки 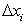 должны стремиться к нулю.
должны стремиться к нулю.
Если в равенстве (193) перейти к пределу при 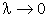 , то получим точное выражение для площади криволинейной трапеции:
, то получим точное выражение для площади криволинейной трапеции:
Таким образом, вычисление площади криволинейной трапеции аbВА свелось к вычислению предела (194).
Задача о вычислении работы переменной силы
Пусть материальная точка M под действием переменной силы 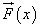 , действующей вдоль оси
, действующей вдоль оси 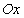 , перемещается вдоль этой оси. Требуется найти работу
, перемещается вдоль этой оси. Требуется найти работу 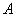 силы
силы 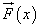 при перемещении материальной точки вдоль оси
при перемещении материальной точки вдоль оси 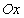 из точки
из точки 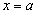 до точки
до точки 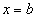 .
.
Из курса физики известно, что при постоянстве силы 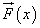 , действующей по направлению движения, искомая работа
, действующей по направлению движения, искомая работа 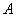 равна произведению
равна произведению 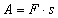 , где F — абсолютная величина силы,
, где F — абсолютная величина силы, 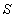 — пройденный путь.
— пройденный путь.
Для отыскания искомой работы по аналогии (см. задачу 1) делим отрезок [a; b], на 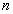 произвольных частей точками
произвольных частей точками 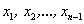 (рис. 5.2
(рис. 5.2 ).
).
Рассмотрим i-ую часть отрезка [a; b], ограниченную точками 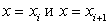 . Возьмем внутри отрезка
. Возьмем внутри отрезка 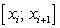 произвольную точку
произвольную точку 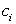 . Найдем значение функции силы
. Найдем значение функции силы 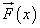 в этой точке:
в этой точке:  . Приближенно работу
. Приближенно работу 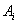 на i-ой части заменим произведением:
на i-ой части заменим произведением:
Поступая аналогично со всеми частями отрезка [a; b], найдем приближенное выражение искомой работы:
Если в равенстве (195) перейти к пределу при 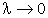 , то получим точное значение искомой работы:
, то получим точное значение искомой работы:
Заметим, что при решении задач 1 и 2 мы делали одни и те же операции:
1) делили отрезок [a; b] на n произвольных частей;
2) внутри каждой части брали по произвольной точке;
3) вычисляли значения заданных величин в этих точках;
4) составляли сумму;
Отвлекаясь от решения конкретных задач, сформулируем общие операции построения сумм (193) и (195), называемых интегральными.
Пусть функция  задана на отрезке [a; b]. Разделим отрезок [a; b] на n произвольных частей точками
задана на отрезке [a; b]. Разделим отрезок [a; b] на n произвольных частей точками 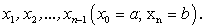
Обозначим через 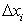 разность
разность 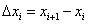 (заметим, что здесь
(заметим, что здесь 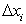 может быть величиной как положительной, так и отрицательной).
может быть величиной как положительной, так и отрицательной).
Внутри каждого отрезка 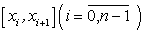 возьмем по произвольной точке
возьмем по произвольной точке 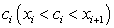 . Находим значение функции
. Находим значение функции 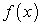 в точках
в точках 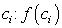 .
.
Составляем сумму произведений:
Переходим к пределу суммы (197) при 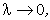 где
где 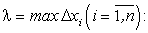
Если существует конечный предел (198) при 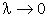 , который не зависит ни от способа деления отрезка [a; b], ни от выбора точек
, который не зависит ни от способа деления отрезка [a; b], ни от выбора точек 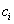 , то этот предел называется определенным интегралом
, то этот предел называется определенным интегралом от функции
от функции 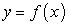 на отрезке [a; b] и символически обозначается так:
на отрезке [a; b] и символически обозначается так:
Здесь 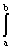 — знак определенного интеграла,
— знак определенного интеграла, 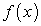 — подынтегральная функция,
— подынтегральная функция, 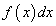 — подынтегральное выражение, х — переменная интегрирования, а и b — нижний и верхний пределы интегрирования соответственно.
— подынтегральное выражение, х — переменная интегрирования, а и b — нижний и верхний пределы интегрирования соответственно.
Таким образом, по определению определенного интеграла имеем:
Из определения определенного интеграла следует, что площадь 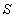 криволинейной трапеции равна:
криволинейной трапеции равна:
а работа А переменной силы 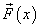 равна:
равна:
В учебнике [1] доказывается, что определенный интеграл (200) существует, если 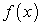 на отрезке [a; b] является кусочно-непрерывной функцией
на отрезке [a; b] является кусочно-непрерывной функцией .
.
-
Постоянный множитель можно выносить за знак определенного интеграла, т.е.
Действительно,
-
Определенный интеграл от алгебраической суммы конечного числа интегрируемых функций равен алгебраической сумме определенных интегралов от слагаемых функций, т.е.
Действительно,
-
При перестановке пределов интеграции знак определенного интеграла меняется на противоположный, т.е. из равенства
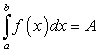 следует равенство
следует равенство 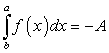 или
или 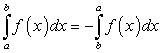 .
.Для доказательства искомого равенства рассмотрим частный случай, когда интегральные суммы интегралов
 ,
, 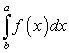 составлены одинаково: то же число точек деления, те же точки деления, те же точки
составлены одинаково: то же число точек деления, те же точки деления, те же точки  . В этих предположениях будем иметь:
. В этих предположениях будем иметь:Следствие. Определенный интеграл с равными пределами интеграции равен нулю, т.е.
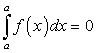 . Действительно, по свойству 3:
. Действительно, по свойству 3: 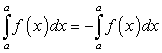 . Отсюда:
. Отсюда: -
Действительно,
Правая часть равенства (203) состоит из суммы, каждый член которой неотрицателен, т.к.
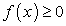 ,
, 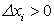 .
.Следовательно, сумма, стоящая в правой части равенства (203), не может быть отрицательной.
-
Если для всех точек
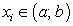 выполняется неравенство
выполняется неравенство 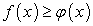 , то:
, то:Действительно, по условию
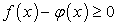 . Отсюда по свойству 4:
. Отсюда по свойству 4:Следовательно, по свойству 2:
-
Если для всех точек
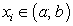 выполняются неравенства
выполняются неравенства 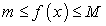 , то:
, то:Свойство 6 называется оценкой определенного интеграла
 .
.Доказательство.
По свойству 5:
Найдем значения крайних интегралов в неравенствах (206):
Отсюда — неравенства (203) перепишутся так:
-
Если
 непрерывна на отрезке [a; b], то на этом отрезке непременно найдется хотя бы одна такая точка
непрерывна на отрезке [a; b], то на этом отрезке непременно найдется хотя бы одна такая точка  , что:
, что:Доказательство. Пусть m и M соответственно наименьшее и наибольшее значения функции
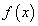 на отрезке [a; b].
на отрезке [a; b].По свойству 6 имеем:
Так как непрерывная функция на замкнутом отрезке принимает сплошь все значения, находящиеся между наименьшим и наибольшим значениями, то внутри отрезка [a; b] найдется по крайней мере одна такая точка х = с, что:
Отсюда находим:
Теорема 24. Производная определенного интеграла по переменному верхнему пределу равна подынтегральной функции на верхнем пределе.
Доказательство. Из определения определенного интеграла следует, что определенный интеграл зависит от функции 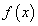 и от пределов интеграции а и b.
и от пределов интеграции а и b.
Пусть верхний предел b определенного интеграла является переменной величиной:
Интеграл (208) можно рассматривать как некоторую функцию от х:
Придавая х приращение 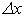 , получим:
, получим:
Обозначим приращение площади через 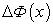
Обратимся к геометрическому представлению интеграла (209) при сделанных предположениях относительно  .
.
Геометрически 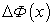 равна площади заштрихованной области на рисунке 5.3
равна площади заштрихованной области на рисунке 5.3 . Эту площадь приближенно можно выразить через площадь прямоугольника с основанием
. Эту площадь приближенно можно выразить через площадь прямоугольника с основанием 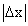 и высотой
и высотой  :
:
Отсюда находим:
Переходя к пределу в равенстве (211) при 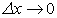 , получим:
, получим:
Отсюда с учетом равенства (211) окончательно находим:
Теорема 25. Если 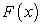 — первообразная функции
— первообразная функции  , то:
, то:
Символически разность 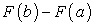 обозначают так:
обозначают так:
Следовательно, по введенному обозначению равенство (209) перепишется так:
Доказательство. По теореме 24 о производной определенного интеграла по переменному верхнему пределу справедливо равенство:
Из данного равенства следует, что 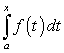 можно рассматривать как первообразную функции
можно рассматривать как первообразную функции 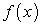 .
.
Так как по условию  также является первообразной функции
также является первообразной функции 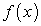 , то по ранее доказанному утверждению их разность равна произвольной постоянной величине
, то по ранее доказанному утверждению их разность равна произвольной постоянной величине 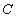 :
:
Если в равенстве (214) положить 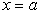 , то можно найти значение С:
, то можно найти значение С:
Так как 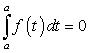 , то отсюда находим, что:
, то отсюда находим, что:
Если в равенстве (214) вместо х взять правую границу отрезка [a; b], то с учетом равенства (215) получим:
Таким образом, из формулы (212) или (213) следует, что для вычисления определенного интеграла надо найти любую первообразную 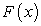 функции
функции 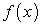 и составить разность
и составить разность  , которая и будет равна значению определенного интеграла.
, которая и будет равна значению определенного интеграла.
Очевидно, при фиксированных пределах интеграции а и b определенный интеграл 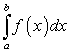 является постоянной величиной. Далее, также очевидно, что определенный интеграл не зависит от переменной интегрирования. Это явно вытекает из равенств:
является постоянной величиной. Далее, также очевидно, что определенный интеграл не зависит от переменной интегрирования. Это явно вытекает из равенств:
В процессе доказательства формулы Ньютона–Лейбница нами получен интересный результат — найдена связь между определенным и неопределенным интегралами:
Пример 1. Вычислить интеграл:
Пример 2.
Теорема 26. Какова бы ни была точка 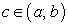 , справедливо равенство:
, справедливо равенство:
Доказательство. Пусть 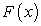 — какая-либо первообразная функции
— какая-либо первообразная функции 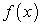 . По формуле Ньютона–Лейбница имеем:
. По формуле Ньютона–Лейбница имеем:
Отсюда находим:
По формуле Ньютона–Лейбница для вычисления определенного интеграла необходимо найти первообразную заданной функции 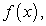 т.е. найти неопределенный интеграл
т.е. найти неопределенный интеграл 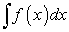 , а затем подставить вместо переменной интегрирования пределы интеграции определенного интеграла.
, а затем подставить вместо переменной интегрирования пределы интеграции определенного интеграла.
На предыдущих занятиях неопределенные интегралы мы находили либо непосредственно с помощью таблиц, либо с помощью замены переменной или подстановки, либо с помощью интегрирования по частям.
Естественной будет постановка следующих вопросов: как изменится выражение определенного интеграла после замены переменной (или подстановки) или интегрирования по частям, по каким формулам вычислять определенные интегралы после таких преобразований?
Перейдем к изложению ответов на поставленные вопросы.
Оказывается, что для вычисления определенных интегралов можно также производить замену переменной интегрирования, причем при каждой замене необходимо находить новые пределы интегрирования для вновь введенной переменной, если не возвращаться к старой переменной.
А именно, справедливо равенство:
если: функция  непрерывна и дифференцируема на отрезке
непрерывна и дифференцируема на отрезке  ;
; 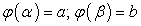 ; функция
; функция 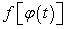 непрерывна на отрезке
непрерывна на отрезке 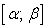 .
.
Если все эти условия выполняются, то справедливо равенство (218). Легко заметить, что все перечисленные условия диктуются равенством (218): подынтегральная функция этого равенства состоит из произведения функций 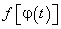 и
и 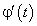 . Для существования определенного интеграла эти функции должны существовать и быть непрерывными.
. Для существования определенного интеграла эти функции должны существовать и быть непрерывными.
Доказательство. Пусть 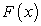 — первообразная функции
— первообразная функции 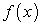 на отрезке [a; b]. По ранее доказанному (замена переменной в неопределенном интеграле) справедливо равенство:
на отрезке [a; b]. По ранее доказанному (замена переменной в неопределенном интеграле) справедливо равенство:
Из равенства (219) следует, что  является первообразной функции
является первообразной функции
Отсюда находим:
Этим доказана справедливость равенства (218).
Замечание. Если при замене переменной отыскание новых пределов интеграции весьма трудоемко или новые пределы интеграции имеют сложный вид, то целесообразно вернуться к старым переменным и подставить старые пределы интеграции.
Пример 3. В качестве примера рассмотрим определенный интеграл 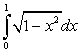 , который вычислим методом замены переменной. Для того чтобы избавиться от иррациональности в подынтегральной функции, сделаем замену переменной:
, который вычислим методом замены переменной. Для того чтобы избавиться от иррациональности в подынтегральной функции, сделаем замену переменной: 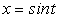 .
.
Пусть функции 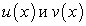 имеют непрерывные производные на отрезке [a; b]. Известно, что
имеют непрерывные производные на отрезке [a; b]. Известно, что
Рассматривая равенство (220) как равенство двух функций, возьмем от обеих его частей определенный интеграл в пределах от а до b:
Отсюда находим:
Равенство (221) и есть формула интегрирования по частям определенного интеграла.
Пример 4.
Пример 5.
Рассмотрим пример на построение интегральной суммы.
Пусть требуется вычислить площадь, ограниченную параболой 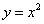 , осью Oх и прямой х = 1.
, осью Oх и прямой х = 1.
-
Разделим отрезок [0; 1] на n равных частей точками
-
В каждом из частичных отрезков выберем по одной точке. Для удобства возьмем правые концы отрезков:
-
Составим интегральную сумму:
Сумма квадратов первых n чисел натурального ряда может быть преобразована по формуле:
Отсюда находим, что
Выполнение непосредственного вычисления определенного интеграла в приведенном примере оказалось возможным только благодаря простой структуре операции суммирования. Для других функций такие вычисления являются весьма проблематичными.
Надо отметить, что такие приемы вычисления проводились еще Архимедом и существовали до появления понятия интеграла.
Поэтому естественным развитием понятия определенного интеграла является выбор целесообразного способа его вычисления — формула Ньютона-Лейбница.
Ниже приведены вычисления определенных интегралов для привития навыков у читателей.
Пример 6.
Пример 7.
Пример 8.
Пример 9.
Пример 10. Вычислить:
Контрольные вопросы
-
В чем отличие определенного интеграла от неопределенного?
-
Чему равен определенный интеграл, если пределы интегрирования — фиксированные действительные числа?
-
Каким условиям должна удовлетворять подынтегральная функция, чтобы определенный интеграл от нее существовал?
-
Какова связь между определенным и неопределенным интегралами?
-
Числом или функцией будет определенный интеграл с переменными пределами интегрирования?
-
По какой формуле вычисляется определенный интеграл?
-
Напишите формулу замены переменной в определенном интеграле.
-
Напишите формулу интегрирования по частям определенного интеграла.
Задания для самостоятельной работы
 .
. . (192)
. (192)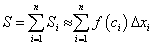 . (193)
. (193)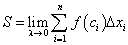 . (194)
. (194)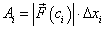 , где
, где 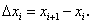
 . (195)
. (195) . (196)
. (196) .
.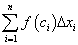 . (197)
. (197)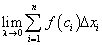 . (198)
. (198)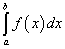 . (199)
. (199)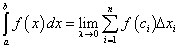 . (200)
. (200)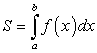 , (201)
, (201) (202)
(202)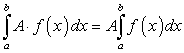 ,
, —
— 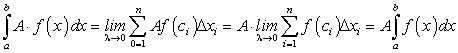 .
.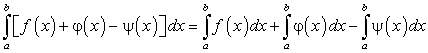 .
.
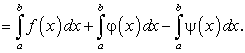
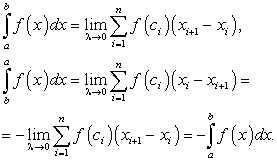
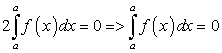 .
.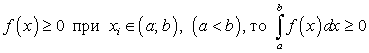 .
.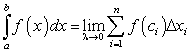 . (203)
. (203)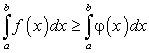 . (204)
. (204)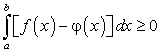 .
.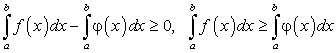 .
.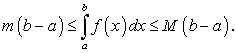 (205)
(205)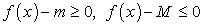 .
.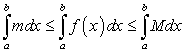 . (206)
. (206)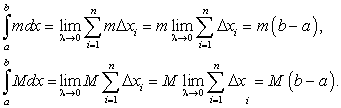
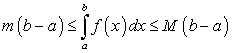 .
.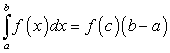 . (207)
. (207)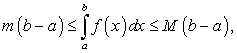 или
или 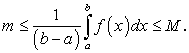
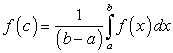 .
.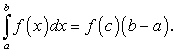
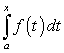 . (208)
. (208)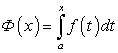 . (209)
. (209) . (210)
. (210)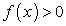 при всех
при всех 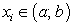 .
.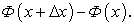
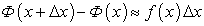 .
.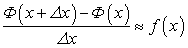 . (211)
. (211)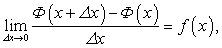 или
или 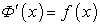 .
. , ч.т.д.
, ч.т.д.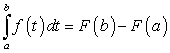 . (212)
. (212)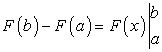
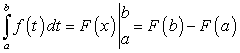 . (213)
. (213) .
.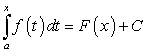 . (214)
. (214) .
.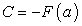 . (215)
. (215) , ч.т.д.
, ч.т.д.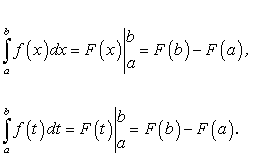
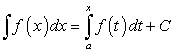 . (216)
. (216)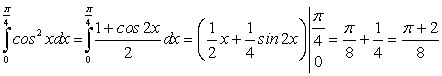 .
.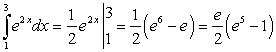 .
. . (217)
. (217)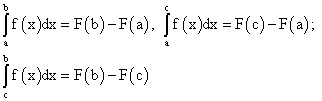
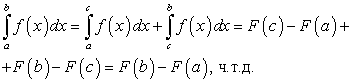
 , (218)
, (218)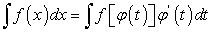 . (219)
. (219)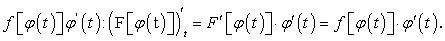
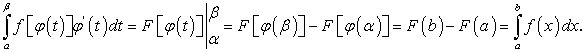
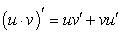 . (220)
. (220)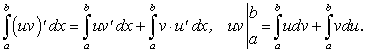
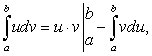 (221)
(221)
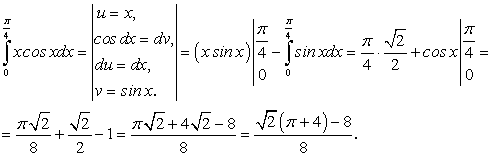
 .
.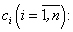
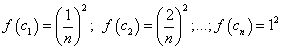
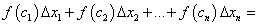 =
= 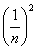 ∙
∙ 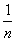 +
+ 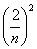 ∙
∙ 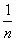 + … +
+ … +  ∙
∙  =
= 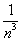
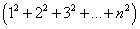
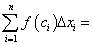
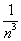
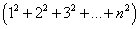 .
.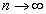 :
: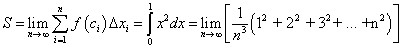 .
.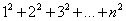 =
=  .
. (кв. ед.).
(кв. ед.).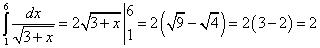 .
. .
.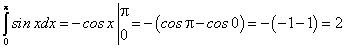 .
.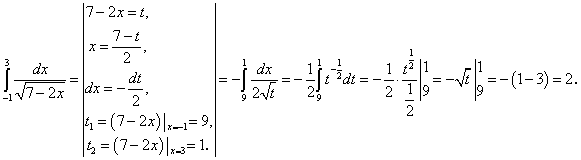

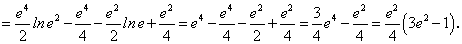
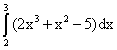 ;
;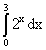 ;
;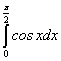 ;
;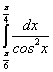 ;
; ;
;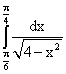 ;
;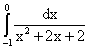 ;
;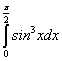 ;
;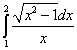 ;
;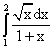 ;
;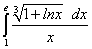 .
. ;
;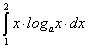 ;
;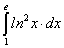 ;
;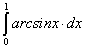 ;
; ;
;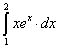 .
.
