Сегодня вы изучите вопросы
-
Дифференциал функции
-
Геометрический смысл дифференциала функции
-
Основные формулы дифференциалов
-
Инвариантность формы первого дифференциала
-
Производные и дифференциалы высших порядков
Изучив тему занятия, вы сможете
-
найти дифференциалы функций;
-
найти производные и дифференциалы высших порядков, заданных функций.
Основные понятия
Пусть на множестве Х задана функция 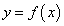 , которая имеет в каждой ее точке производную:
, которая имеет в каждой ее точке производную:
По теореме о существовании предела переменной имеем:
Отсюда находим:
Приращение 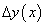 функции
функции 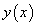 в произвольной точке
в произвольной точке 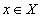 в равенстве (114) представлено в виде суммы двух слагаемых, каждое из которых стремится к нулю при
в равенстве (114) представлено в виде суммы двух слагаемых, каждое из которых стремится к нулю при 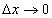 , т.е. является б.м.в. при
, т.е. является б.м.в. при 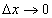 . Однако второе слагаемое в правой части равенства (114) является б.м.в. более высокого порядка, чем первое, в точках, где производная отлична от 0.
. Однако второе слагаемое в правой части равенства (114) является б.м.в. более высокого порядка, чем первое, в точках, где производная отлична от 0.
Следовательно, первое слагаемое, линейное относительно 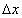 , является главной частью приращения дифференцируемой функции
, является главной частью приращения дифференцируемой функции 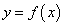 . Эта часть приращения функции называется дифференциалом функции
. Эта часть приращения функции называется дифференциалом функции 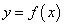 и символически обозначается через
и символически обозначается через 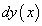 :
:
Найдем дифференциал независимой переменной х:
Из равенства (115) с учетом (116) имеем:
Из формулы (117) следует, что производную 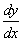 по Лейбницу можно рассматривать как дробь, где
по Лейбницу можно рассматривать как дробь, где 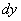 — числитель, а
— числитель, а 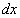 f — знаменатель.
f — знаменатель.
Следовательно, производную 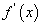 функции
функции 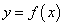 можно рассматривать как отношение дифференциала функции к дифференциалу независимой переменной.
можно рассматривать как отношение дифференциала функции к дифференциалу независимой переменной.
В приближенных вычислениях приращение функции 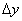 заменяют ее дифференциалом
заменяют ее дифференциалом 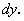 Как было доказано выше, второе слагаемое (114) есть б.м.в. более высокого порядка, а следовательно, разность
Как было доказано выше, второе слагаемое (114) есть б.м.в. более высокого порядка, а следовательно, разность 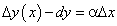 есть б.м.в. при
есть б.м.в. при 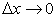 .
.
Поэтому можно положить, что:
или
Отсюда находим, что:
Формула (119) позволяет выразить приближенно новое значение функции через старое и дифференциал этой функции.
Например, пусть требуется найти приближенное значение корня 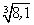 . По форме заданной величины находится функция:
. По форме заданной величины находится функция: 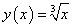 .
.
По формуле (119) находим:
Пусть функция 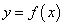 дифференцируема на множестве Х; тогда на плоскости Оху график функции представляется гладкой линией L (в каждой точке этой линии имеется единственная касательная) (рис. 2.10
дифференцируема на множестве Х; тогда на плоскости Оху график функции представляется гладкой линией L (в каждой точке этой линии имеется единственная касательная) (рис. 2.10 ).
).
Пусть М — произвольная точка графика функции 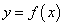 .
.
Построим в точке М касательную 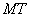 к графику функции
к графику функции 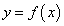 .
.
Пусть т. 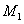
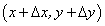 — точка графика функции с абсциссой
— точка графика функции с абсциссой 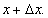 Сделаем дополнительные построения (см. рис. 2.10).
Сделаем дополнительные построения (см. рис. 2.10).
По рисунку 2.10, 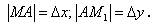 Найдем величину
Найдем величину 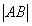 :
:
Правая часть равенства (120) есть выражение дифференциала функции 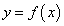 .
.
Следовательно,
т.е. левая часть равенства (121) есть приращение ординаты касательной. Отсюда краткое заключение.
Дифференциал функции геометрически представляет приращение ординаты касательной.
представляет приращение ординаты касательной.
Пусть функции 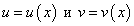 дифференцируемы на множестве Х. Найдем формулы дифференциалов для функций:
дифференцируемы на множестве Х. Найдем формулы дифференциалов для функций:
По определению дифференциала функции и формул дифференцирования имеем:
В частности, если 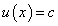 — константа или
— константа или 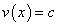 — константа, получим:
— константа, получим:
Найдем дифференциалы основных элементарных функций:
Из полученных равенств следует, что формулы дифференциалов аналогичны формулам для производных функции 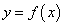 с той лишь только разницей, что вместо производных
с той лишь только разницей, что вместо производных 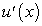 мы имеем дифференциалы
мы имеем дифференциалы 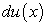 .
.
Пусть функция 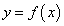 дифференцируема на множестве Х. Дифференциал первого порядка этой функции, как известно, равен:
дифференцируема на множестве Х. Дифференциал первого порядка этой функции, как известно, равен:
Пусть 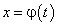 , где
, где 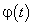 — дифференцируемая функция на множестве Т, областью значений которой является множество Х. В этом случае переменная y является сложной функцией переменной t на множестве Т:
— дифференцируемая функция на множестве Т, областью значений которой является множество Х. В этом случае переменная y является сложной функцией переменной t на множестве Т:
Найдем дифференциал сложной функции:
Мы видим, что форма первого дифференциала не изменилась. В этом и состоит инвариантность формы первого дифференциала .
.
Рассмотрим функцию 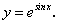 Первая ее производная равна
Первая ее производная равна 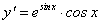 , т.е. тоже является функцией от х на множестве
, т.е. тоже является функцией от х на множестве 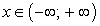 .
.
Найдем вторую ее производную:
Мы видим, что вторая производная также является функцией от х, которая, в свою очередь, может иметь производную, уже третьего порядка, и т.д.
Производной n-го порядка от функции 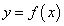 называется производная от производной (
называется производная от производной (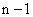 )-го порядка:
)-го порядка:
В некоторых частных случаях иногда удается найти формулу для производной n-го порядка.
Пусть требуется найти дифференциал функции 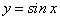 :
:
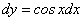 , т.е. дифференциал функции, есть, вообще говоря, тоже функция — поэтому, в свою очередь, может иметь дифференциал (дифференциал второго порядка):
, т.е. дифференциал функции, есть, вообще говоря, тоже функция — поэтому, в свою очередь, может иметь дифференциал (дифференциал второго порядка):
Дифференциалом n-го порядка называется дифференциал от дифференциала (n — 1)-го порядка:
называется дифференциал от дифференциала (n — 1)-го порядка: 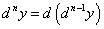 .
.
По аналогии:
Формулу (124) легко доказать методом полной математической индукции.
Пусть формула (124) справедлива для дифференциала
Покажем, что в этих предположениях она верна и для дифференциала (k + 1)-го порядка:
Из равенства (124) следует, что 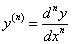 , т.е. n-ую производную, по Лейбницу, можно рассматривать как дробь, где
, т.е. n-ую производную, по Лейбницу, можно рассматривать как дробь, где 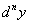 — числитель, а
— числитель, а 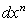 — знаменатель.
— знаменатель.
Рассмотрим приложения изложенной теоремы.
Пример 1. Дана металлическая квадратная пластинка с ребром х = 100 мм. При нагревании ребро пластинки удлиняется на ∆х = 0,1 мм. Насколько увеличится при этом площадь пластинки?
Пусть S(х) — первоначальная площадь пластинки, а ∆S — приращение этой площади после нагревании.
Найдем приближенное приращение площади пластинки, заменив ее полным дифференциалом:
∆S ≈ ds = (x2)'dx = 2x ∙ dx = 2x ∙ ∆x.
По условию задачи х = 100 мм, ∆x = 0,1 мм.
Отсюда находим, что:
∆S ≈ 2 ∙ 100 мм ∙ 0,1 мм = 20 мм2.
Для оценки погрешности вычисления найдем полное приращение по формуле:
∆S = (х + ∆x)2 — х2 = 2х ∙ ∆х + ∆х2.
Следовательно, погрешность замены равна:
∆х2 = (0,1 мм)2 = 0,01 мм2.
Последнее и есть неглавная часть приращения функции 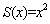 , равная
, равная
Пример 2. Найти дифференциал функции y = xn.
По определению дифференциала функции имеем:
Пример 3. Найти дифференциал функции y = ax.
Пример 4. Найти дифференциал функции у = sinx.
Пример 5. Заменив приращение функции дифференциалом, найти приближенное значение arctg 1,02.
Формула 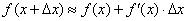 применительно к данной функции перепишется так:
применительно к данной функции перепишется так:
В данном случае х + ∆x = 1,02, х = 1, ∆x = 0,02.
Отсюда можно положить, что:
Данное утверждение можно доказать методом полной математической индукции.
Контрольные вопросы
-
Из каких двух частей состоит полное приращение функции?
-
Чем является для функции ее линейная часть относительно приращения независимой переменной?
-
Сравните неглавную часть с главной частью. Ваши выводы.
-
Может ли функция иметь дифференциал в точке, если она не имеет производной в этой точке?
-
Каков геометрический смысл дифференциала функции?
-
В чем состоит инвариантность формы первого дифференциала?
Задания для самостоятельной работы
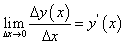 . (113)
. (113)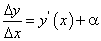 , где
, где 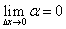 .
.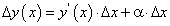 . (114)
. (114)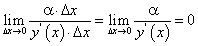 .
.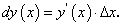 (115)
(115)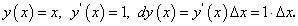
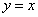 , то:
, то: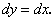 (116)
(116)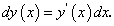 (117)
(117)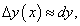 (118)
(118)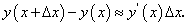
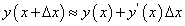 . (119)
. (119)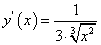 . Здесь
. Здесь 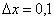 .
.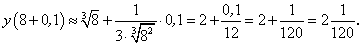
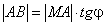 .
.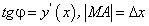 , то:
, то: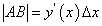 . (120)
. (120)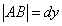 , (121)
, (121)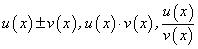
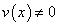 ).
).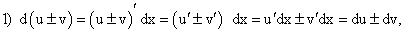
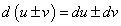 .
.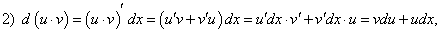
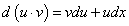 .
.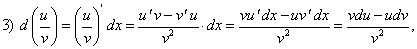
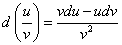 .
.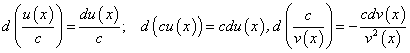 .
.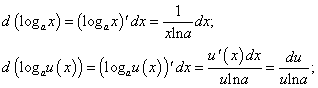
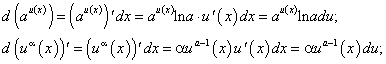
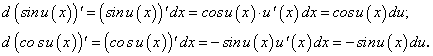
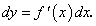 (122)
(122)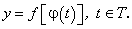 (123)
(123)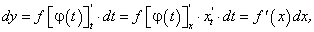
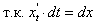 .
.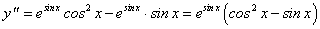 .
.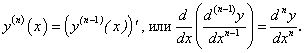 .
.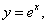
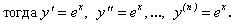
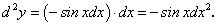
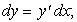
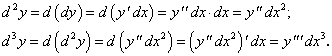
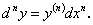 (124)
(124)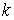 -го порядка, т.е.
-го порядка, т.е.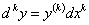 . (125)
. (125)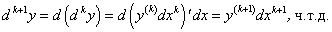
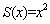 .
.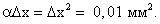
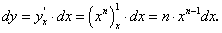
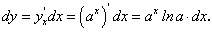
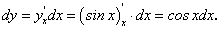
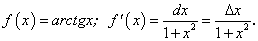
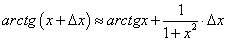 .
.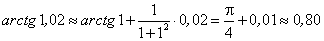 .
.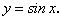
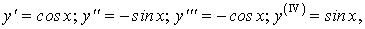 или
или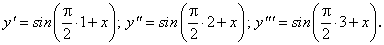
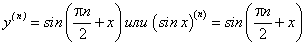 .
.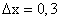 по определению дифференциала.
по определению дифференциала.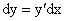 :
: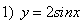 ;
;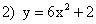 ;
;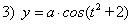 ;
;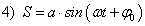 ;
;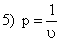 ;
;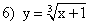 ;
;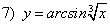 ;
; ;
;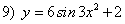 .
.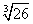 .
.