Задание 1
Комментарий.
-
При упрощении данного выражения следует записать его или с использованием радикалов, или с использованием степеней.
-
Следует использовать формулу «Квадрат суммы» и свойства степеней (в том числе свойство степени с отрицательным показателем).
-
Необходимо помнить, как выполняется деление двух дробей.
-
Нужно обратить внимание на то, что при работе с дробями сокращаются исключительно множители.
Задание 2
Задание 3
Задание 4
Комментарий.
-
Данное выражение можно преобразовывать, выделяя полный квадрат из выражений, стоящих под знаком корня.
-
Следует помнить, что корень из квадрата некоторого выражения равен модулю этого выражения, а не самому выражению.
-
Альтернативным способом выполнения преобразований является возведение выражения
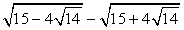 в квадрат. Т.е., предположим, что
в квадрат. Т.е., предположим, что 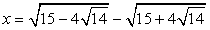 . Тогда
. Тогда 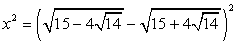 . Далее следует применить формулы сокращенного умножения, и, решая окончательное уравнение вида x2
= a, выбрать нужный корень, ориентируясь на знак исходного выражения (
. Далее следует применить формулы сокращенного умножения, и, решая окончательное уравнение вида x2
= a, выбрать нужный корень, ориентируясь на знак исходного выражения (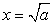 или
или 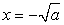 ).
).
Задание 5
Задание 6
Задание 7
Задание 8
Комментарий.
-
Для сокращения дроби следует по возможности полностью разложить на множители числитель и знаменатель.
-
С целью разложения на множители числителя нужно обратить внимание на возможность группировки слагаемых (на способ группировки указывает четное количество слагаемых и пропорциональность коэффициентов).
-
Для разложения на множители знаменателя следует использовать формулы корней квадратного уравнения (или теорему, обратную теореме Виета).
Задание 9
Найдите наименьшее значение выражения 8x2 + 2y2 — 4xy + 4x + 2y + 3.
Задание 10
Найдите наибольшее значение выражения: 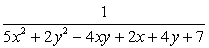 .
.
Задание 11
Вычислите значение выражения: 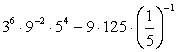 .
.
Задание 12
Вычислите значение выражения: 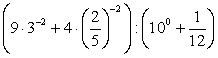 .
.
Задание 13
Вычислите значение выражения: 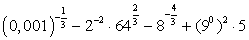 .
.
Задание 14
Вычислите значение выражения: 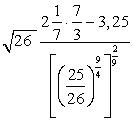 .
.
Задание 15
Упростите выражение и вычислите его значение при а = 9:
Задание 16
Упростите выражение и вычислите его значение при х = 2:
Задание 17
Упростите выражение и вычислите его значение при заданных значениях параметров:
Задание 18
Вычислите значения выражений:
Задание 19
Упростите выражения:
Комментарий к заданию «а».
-
Упрощение заданного выражения лучше всего выполнять по действиям, обращая внимание на их порядок (первое и второе действия — приведение сумм в двух квадратных скобках к общему знаменателю).
-
Далее следует вспомнить, каким образом выполняется деление двух дробей и воспользоваться свойством степени с отрицательным показателем.
Задание 20
Сократите дроби:
Комментарий к заданию «а».
-
Необходимо рассмотреть числитель и знаменатель дроби Eqn_zadanie_01-43.gif отдельно, т.к. сразу сокращение не возможно (сокращаются только одинаковые множители, содержащиеся в числителе и знаменателе).
-
Для разложения числителя на множители следует решить соответствующее квадратное уравнение.
-
Чтобы разложить знаменатель на множители нужно вынести общий множитель за скобку. Необходимо отметить, что вынесение общего множителя за скобку — самый простой способ разложения на множители, которые нужно использовать в первую очередь (до использования более сложных методов — формул сокращенного умножения, способа группировки и др.).
Комментарий к заданию «b».
-
Следует обратить внимание на вид знаменателя: четное количество слагаемых и пропорциональность коэффициентов многочлена говорит о том, что нужно применять способ группировки.
-
Для разложения числителя на множители необходимо применить формулу «разность квадратов».
Задание 21
Пользуясь теоремой Виета, вычислите значения выражений:
a. 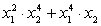 , если x1
и x2
— корни уравнения
, если x1
и x2
— корни уравнения 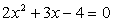 ;
;
b. 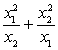 , если x1
и x2
— корни уравнения
, если x1
и x2
— корни уравнения 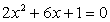 ;
;
c. 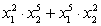 , если x1
и x2
— корни уравнения
, если x1
и x2
— корни уравнения 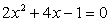 ;
;
d. 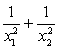 , если x1
и x2
— корни уравнения
, если x1
и x2
— корни уравнения 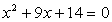 ;
;
e. 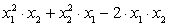 , если x1
и x2
— корни уравнения
, если x1
и x2
— корни уравнения 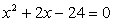 ;
;
f. 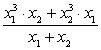 , если x1
и x2
— корни уравнения
, если x1
и x2
— корни уравнения 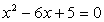 ;
;
g. 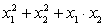 , если x1
и x2
— корни уравнения
, если x1
и x2
— корни уравнения 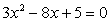 ;
;
h. 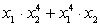 , если x1
и x2
— корни уравнения
, если x1
и x2
— корни уравнения 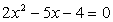 ;
;
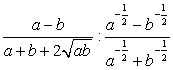 .
.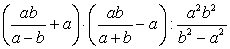 .
.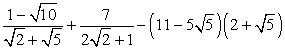 .
.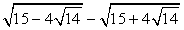 .
.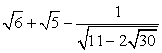 .
.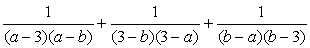 .
.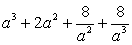 , если
, если 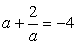 .
.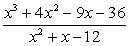 .
.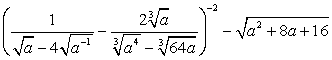
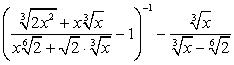
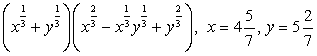
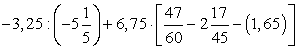 ;
;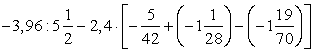 ;
;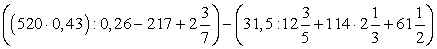 ;
;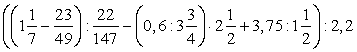 ;
;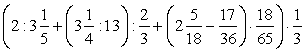 ;
;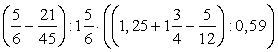 ;
;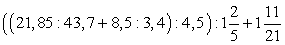 ;
;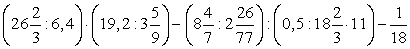 ;
;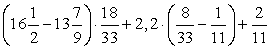 ;
;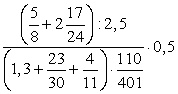 .
.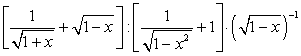 ;
;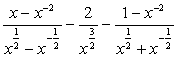 ;
;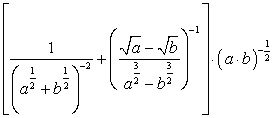 ;
;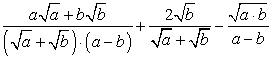 ;
;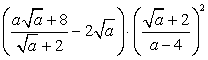 ;
;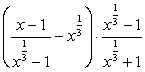 ;
;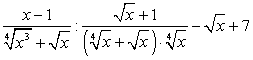 ;
;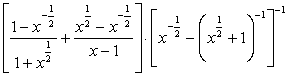 ;
;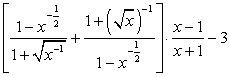 ;
;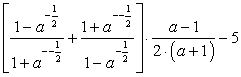 .
.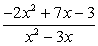 ;
;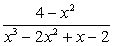 ;
;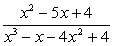 ;
;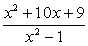 ;
;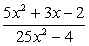 ;
;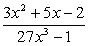 ;
;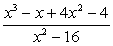 ;
;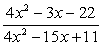 ;
;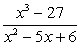 ;
;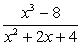 .
.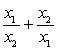 , если
, если 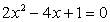 ;
;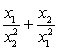 , если
, если 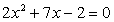 .
.
