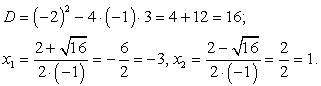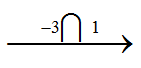Уравнения подразделяются на несколько групп:
1) линейные уравнения;
2) квадратные уравнения;
3) дробно-рациональные уравнения;
4) уравнения высших степеней.
Корнем уравнения с одним неизвестным называют значение неизвестного, при котором уравнение обращается в верное равенство.
называют значение неизвестного, при котором уравнение обращается в верное равенство.
Уравнением с одним неизвестным x называют уравнение вида ax = b, где x — неизвестное, a и b — некоторые числа; a называют коэффициентом
x называют уравнение вида ax = b, где x — неизвестное, a и b — некоторые числа; a называют коэффициентом или переменной, b — свободным членом
или переменной, b — свободным членом .
.
Квадратным уравнением с одним неизвестным x называют уравнение вида ax2
+ bx + с = 0, где a, b, с — некоторые числа (коэффициенты уравнения), причем a ≠ 0; aназывают первым (старшим) коэффициентом
с одним неизвестным x называют уравнение вида ax2
+ bx + с = 0, где a, b, с — некоторые числа (коэффициенты уравнения), причем a ≠ 0; aназывают первым (старшим) коэффициентом , b — вторым коэффициентом
, b — вторым коэффициентом , c — свободным членом.
, c — свободным членом.
Если в квадратном уравнении хотя бы один коэффициентов равен 0 (кроме, конечно, коэффициента при x2
), то уравнение называют неполным квадратным уравнением .
.
Выражение вида D = b2
– 4ac называют дискриминантом у квадратного уравнения ax2
+ bx + с = 0. По дискриминанту у квадратного уравнения определяют, сколько у него корней:
ax2
+ bx + с = 0. По дискриминанту у квадратного уравнения определяют, сколько у него корней:
1) если D > 0, то уравнение имеет два различных корня;
2) если D = 0, то уравнение имеет один корень или два совпавших корня;
3) если D < 0, то уравнение корней не имеет.
Если D > 0, то квадратное уравнение имеет два различных корня, которые вычисляются по формуле:
или
Если D = 0, то квадратное уравнение имеет один корень или два одинаковых корня.
Если D < 0, то квадратное уравнение корней не имеет.
Пример 3.1.
Решите квадратное уравнение: 2x2 – 3x – 5 = 0.
Ответ: x1 = 2,5; x2 = -1.
Теорема Виета гласит, что если приведенное квадратное уравнение x2
+ px + q = 0 имеет корни, то сумма корней этого уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену, т.е. если x1
и x2
— корни уравнения x2
+ px + q = 0, то
гласит, что если приведенное квадратное уравнение x2
+ px + q = 0 имеет корни, то сумма корней этого уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену, т.е. если x1
и x2
— корни уравнения x2
+ px + q = 0, то
Согласно обратной теореме Виета , если сумма двух чисел равна второму коэффициенту приведенного квадратного уравнения, взятому с противоположным знаком, а их произведение равно свободному члену, то эти числа являются корнями приведенного квадратного уравнения, т.е. если выполняются условия:
, если сумма двух чисел равна второму коэффициенту приведенного квадратного уравнения, взятому с противоположным знаком, а их произведение равно свободному члену, то эти числа являются корнями приведенного квадратного уравнения, т.е. если выполняются условия:
то x1 и x2 — корни уравнения x2 + px + q = 0.
Задание 1
Решите уравнение: 8 – 2(6x + 1) = -2x - 3.
Решение
Раскроем скобки:
8 – 12x – 2 = -2x – 3.
Перенесем неизвестные влево, известные — вправо:
-12x + 2x = -3 + 2 – 8
-10 x = -9
x = 0,9.
Задание 2
Решение
Перенесем все слагаемые в левую часть:
Приведем слагаемые к общему знаменателю (x2 - 4 разложим по формуле сокращенного умножения):
Раскроем скобки в числителе:
Данное уравнение можно представить в виде системы. В системе приравниваем числитель к нулю, а также делим его на 2. Знаменатель не равен нулю, так как на нуль делить нельзя:
Таким образом, решая квадратное уравнение, находим его корни: x1 = 3, x2 = -2. Так как -2 и 2 не входят в ОДЗ, корнем данного уравнения и ответом является только 3.
Следует обратить внимание, что иногда при разложении числителя по формуле сокращенного умножения не всегда получается общий знаменатель состоящий из двух скобок. Например:
Если в данном в примере разложить 9 – x2 = (3 – x) ∙ (3 + x), то общий знаменатель будет состоять из 4-х скобок: (3 – x) ∙ (3 + x) ∙ (x – 3) ∙ (x + 3).
Таким образом, в исходном примере из знаменателя второй дроби выносим знак минус перед дробью, меняя тем самым знаки в знаменателе. Получим:
Теперь при разложении знаменателя второй дроби по формуле сокращенного умножения получаем: x2 – 9 = (x – 3) ∙ (x + 3). Общий знаменатель будет состоять их двух скобок. Дальнейшее решение продолжается по рассмотренному выше алгоритму.
Задание 3
Решите уравнение: x3 – 6x2 – 31x + 36 = 0.
Решение
Если данное уравнение имеет целый корень, то он является делителем числа 36. Подберем корень. Как правило, корнем является одно из чисел: -1, -2, -3, 1, 2, 3.
Проверка показывает, что число 1 является корнем данного уравнения (для этого подставили 1 вместо x).
Левая часть уравнения x3 – 6x2 – 31x + 36 = 0 может быть представлена в виде:
(x – 1) ∙ P(x), где P(x) — многочлен второй степени.
Так как корень 1, делим уравнение на x - 1 (если корнем является отрицательное число, например, -1, то делим на x + 1).
Деление уравнения в столбик предполагает следующие этапы:
1) делим x3 на x, получаем x2 ;
2) x2 умножаем, как бы в обратную сторону, сначала на x, получаем x3 , затем на -1, получаем -x2 (действия видны, когда из общего уравнения вычитаем x3 – x2 );
3) получаем -5x2 ;
4) сносим -31x, получаем выражение -5x2 – 31x;
5) алгоритм повторяется: делим -5x2 на x, получаем -5x;
6) умножаем -5x, как бы в обратную сторону, сначала на x, получаем -5x2 , затем на -1, получаем 5x (действия видны, когда из выражения -5x2 – 31x вычитаем -5x2 + 5x), и так далее по алгоритму решения, пока не получим нуль.
В итоге исходное уравнение можно представить в виде:
x3 – 6x2 – 31x + 36 = (x – 1) ∙ (x2 – 5x – 36) = 0.
Находим корни квадратного уравнения:
x2 – 5x – 36 = 0
x1 = 9
x2 = -4
Полученные значения и найденный в начале методом подбора корень 1 и будут корнями рассмотренного уравнения.
Ответ: -4; 1; 9.
Всякое значение неизвестного, при котором данное неравенство с неизвестным обращается в верное числовое неравенство, называется решением неравенства . Решить неравенство — значит найти все его решения или доказать, что их нет.
. Решить неравенство — значит найти все его решения или доказать, что их нет.
Неравенство вида ax + b > 0 (< 0, ≥ 0, ≤ 0), где x — неизвестное, a и b — некоторые действительные числа (a ≠ 0), называется неравенством первой степени , или линейным неравенством.
, или линейным неравенством.
Неравенство вида ax2
+ bx + c > 0 (< 0, ≥ 0, ≤ 0), где a ≠ 0, называют неравенством второй степени с одним неизвестным, или квадратным неравенством.
с одним неизвестным, или квадратным неравенством.
a, b, с — действительные числа.
Если a > b и b > c, то a > c.
Если a > b и c — положительное число (c > 0), то a + с > b + c.
Если a > b и c — положительное число (c > 0), то ac > bc.
Если a > b и c — отрицательное число (c< 0), то ac < bc.
Решение квадратных неравенств ax2 + bx + c > 0 (< 0, ≥ 0, ≤ 0), состоит из пяти этапов.
-
Вводим соответствующую функцию y = ax2 + bx + c.
-
Определяем направление ветвей параболы y = ax2 + bx + c: при a > 0 ветви параболы направлены вверх; при a < 0 ветви параболы направлены вниз.
-
Находим нули функции, т.е. решаем уравнение ax2 + bx + c = 0.
-
Если уравнение имеет корни, то отмечаем корни на координатной прямой и схематически рисуем параболу в соответствии с направлением ветвей. Если уравнение не имеет корней, то схематически рисуем параболу в соответствии с направлением ветвей.
-
Находим решение неравенства с учетом знака неравенства.
Задание 1
Решение
Решение данных примеров сопряжено с определение знаков скобок.
Сначала определяется знак скобки без неизвестной. В данном примере это первая скобка.
Так как 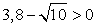 , чтобы все выражение было больше нуля (это видно из примера), вторая скобка должна иметь знак плюс, т.е. быть также больше нуля: 2 – 4x > 0.
, чтобы все выражение было больше нуля (это видно из примера), вторая скобка должна иметь знак плюс, т.е. быть также больше нуля: 2 – 4x > 0.
Решая данное неравенство, получим:
-4x > -2
Ответ: x < 0,5.
Задание 2
Решите неравенство: -x2 – 2x + 3 ≥ 0.
Решение
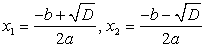
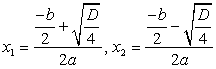 .
. 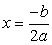 .
. 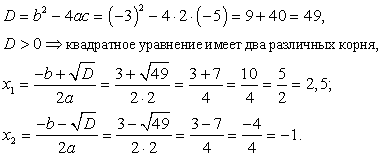
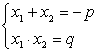
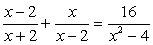 .
. 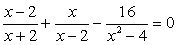 .
. 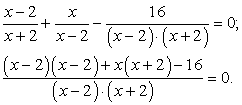
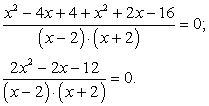
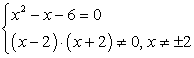
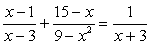 .
. 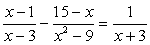 .
. 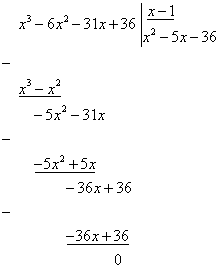
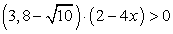 .
.