Например, вычислите выражения:

ax² + bx + с = а (x – x₁ ) (x – x₂ ), a ≠ 0, где x₁ и x₂  — корни трехчлена ax² + bx + c.

Например, упростите выражение:

Рассмотрим числитель. Чтобы разложить его на множители, решим уравнение x² + 6x + 6 = 0, применив формулу разложения квадратного трехчлена на множители.

Найдите значение выражения 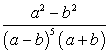при a – b = 2.

Упростим выражение, используя формулу сокращенного умножения:

.

На координатной прямой отмечены точки А, В, С, D. Одна из точек соответствует числу 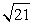. Какая это точка?

Ближайшее число, из которого извлекается 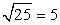, следовательно, 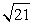соответствует точке D, которая ближе всего расположена к 5 на координатной прямой.

Найдите значение выражения 0,7x³ – 2,1x² + 4 при x = -2.

Подставляем вместо x данное значение и находим значение выражения:

0,7 ∙ (-2)³ – 2,1 ∙ (-2)² + 4 = 0,7 ∙ (-8) – 2,1 ∙ 4 + 4 = -10.

Также можно вынести x² за скобку, упростив выражение.

Из формулы Джоуля—Ленца Q = I² Rt выразите силу тока I в виде дроби.

В какое из приведенных ниже выражений можно преобразовать выражение (7 – x) ∙ (x – 4)?

1) -(7 – x) ∙ (4 – x);

2) (7 – x) ∙ (4 – x);

3) (x – 7) ∙ (x – 4);

4) -(x – 7) ∙ (4 - x).

Знак минус, стоящий перед скобкой в выражении под номером 1 и 4, можно внести только в одну из скобок, изменив в ней знаки. Выражение под номером 4 не подходит, так как в нем необходимо менять знаки в обеих скобках. Поэтому правильный ответ — выражение под номером 1, так как в нем необходимо изменить знаки только в одной, второй скобке.

Соотнесите каждое выражение с множеством значений переменной t, при которых оно имеет смысл.

А)	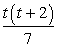1) t ≠ 0, t ≠ -2
Б)	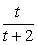2) t ≠ -2
В)	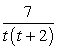3) t — любое число

Знаменатель не должен быть равен нулю. Поэтому соотнесение выражений осуществляется по принципу исключения нуля в знаменателе представленных дробей. Так как знаменатель дроби A это число, следовательно, t в данном случае — любое число. Знаменатель второй дроби содержит переменную t, и она не должна быть равна -2, так как в этом случае знаменатель обращается в нуль. Знаменатель третьей дроби также содержит переменную t. Чтобы исключить обращение знаменателя в нуль t не должна быть равна 0 и -2.

Какой из следующих квадратных трехчленов нельзя разложить на линейные множители?

1) x² – 14x + 49;

2) x² – 13x + 40;

3) x² – 2x + 4;

4) x² – 11x - 17.

Чтобы ответить на поставленный вопрос, необходимо определить дискриминанты заданных квадратных трехчленов. Где дискриминант будет отрицательным, тот и нельзя разложить на линейные множители. В данном случае отрицательный дискриминант будет у квадратного трехчлена под номером 3.

Упростите выражение .

Данное задание предусматривает применение формул сокращенного умножения. Числитель первой дроби по формуле сокращенного умножения можно представить как (5c – 3d) ∙ (5c + 3d). В знаменателе второй дроби необходимо 5 вынести за скобку, получим: 5(3d + 5c). Таким образом, исходное выражение примет вид:

.

Теперь выражение можно сократить. Числитель первой дроби и знаменатель второй можно сократить на скобку (5c + 3d). Знаменатель первой дроби и числитель второй можно сократить на c. Получим:

.

Сократите дробь: .

Решение подобных примеров сопряжено с использованием метода группировки. В данном примере группировать будем знаменатель дроби. Напомним, что суть метода группировки заключается в том, чтобы получить две одинаковые скобки, которые в последующем образуют одну скобку. Покажем применение данного метода на нашем примере:

.

Теперь необходимо решить, что будем выносить из скобок. Необходимо обратить внимание на числитель дроби. Так как двойка в числителе имеет знак минус, двойку в знаменателе из первой скобки будем выносить со знаком минус. Тройка в числителе имеет знак плюс, тройку в знаменателе из второй скобки будем выносить со знаком плюс. Получим:

.

Необходимо помнить, что знаки выражения можно менять, вынося знак минус из скобки перед скобкой или перед всей дробью. Этот прием используется практически во всех примерах, относящихся к данному заданию с целью группировки (получения одинаковой скобки), либо выражений, которые можно сократить, упростив вид дроби.

Разложим вторую скобку в знаменателе по формуле сокращенного умножения. Получим:

.

Таким образом, мы получили одинаковую скобку в знаменателе (c – d). Оставшиеся значения знаменателя образуют выражение -2 + 3(c + d) или, если раскрыть скобку, — 3c + 3d - 2. Получим:

.

Сократив числитель и знаменатель дроби, получим:

.

Данное выражение и будет ответом рассматриваемого примера.
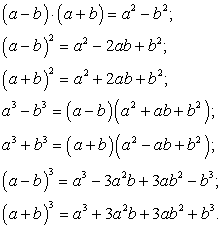
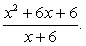
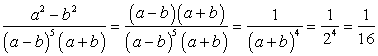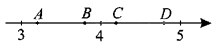
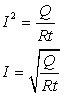
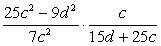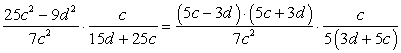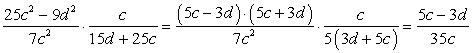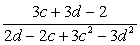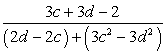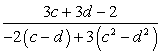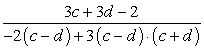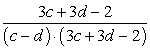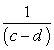