Понятие степени с целым показателем
Определение. Степенью числа a с натуральным показателем n называется число, записываемое как an
и определяемое по правилу:
называется число, записываемое как an
и определяемое по правилу:
Например:
Определение. Степенью числа a (a ≠ 0) с целым показателем m называется число, записываемое как am
и определяемое по правилу:
называется число, записываемое как am
и определяемое по правилу:
Выражения «нуль в нулевой степени» и «нуль в отрицательной степени» не определены.
Если основанием степени является обыкновенная дробь, то удобно использовать правило, которое следует непосредственно из определения:
Например:
Свойства степени с целым показателем
m, n — целые числа, p ≠ 0
Задание 1
Какое из следующих выражений равно дроби: 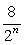 ?
?
Решение
Чтобы ответить на данный вопрос, воспользуемся свойством степени с целым показателем. При делении показатели степеней с одинаковым основанием вычитаются. Таким образом, если 8 представить как 23 , получим, что:
Задание 2
Микропроцессор за секунду совершает 250 тыс. операций. Как эта величина записывается в стандартном виде?
Воспользуемся правилом записи чисел с использованием степеней числа 10. Если положительное число a представлено в виде a1 ∙ 10n , где 1 ≤ a1 < 10, n — целое число, то говорят, что число a записано в стандартном виде.
В нашем примере, чтобы число 250000 представить в стандартном виде, необходимо, чтобы запятая стояла после числа 2, что будет удовлетворять условию, что 1 ≤ a1 < 10. Тогда получим число 2,5. И, чтобы данное число соответствовало исходному, его необходимо умножить на 105 . То есть если запятую перенести на пять знаков вправо (так как степень положительная, поэтому вправо), получим 250000.
Ответ: 2,5 ∙ 105 .
Задание 3
Запишите числа в стандартном виде:
1) 0,0069;
2) 98000.
Решение
-
Чтобы представить число 0,0069 в стандартном виде, необходимо записать его в виде a1 ∙ 10n , где 1 ≤ a1 ≤ 10. Перенесем запятую в числе 0,0069 на три знака вправо, только тогда получим 1 ≤ 6,9 ≤ 10. После переноса запятой получим число 6,9, которое больше числа 0,0069 в 103 раз. Чтобы число не изменилось, результат нужно умножить на 10-3 . Получаем: 0,0069 = 6,9 ∙ 10-3 .
-
Чтобы представить число 98000 в стандартном виде, необходимо записать его в виде a1 ∙ 10n , где 1 ≤ a1 ≤ 10. Перенесем запятую в числе 98000 на четыре знака влево, только тогда получим 1 ≤ 9,8 ≤ 10. После переноса запятой получим число 9,8, которое меньше числа 98000 в 10-4 раз. Чтобы число не изменилось, результат нужно умножить на 104 . Получаем: 98000 = 9,8 ∙ 104 .
Примечание.
Если преобразование числа происходит с переносом запятой слева направо, то осуществляется действие деление на 10n
. Записываем как 0,0069 = 6,9 ∙ 10-3
, выражение при преобразовании равняется 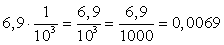 .
.
Если преобразование числа происходит с переносом запятой справа налево, то осуществляется произведение на 10n (записываем как 98000 = 9,8 ∙ 104 , выражение при преобразовании равняется 9,8 ∙ 10000 = 98000).
Задание 4
Из чисел 1,130 ∙ 106 ; 5,713 ∙ 105 ; 4,011 ∙ 106 ; 2,315 ∙ 105 выберите наибольшее.
Решение
Данное задание предполагает оценку значений сначала по степени — наибольшая степень шестая. Таких значений два: первое и третье. Затем оцениваем первый множитель: 4,011 больше 1,130. Поэтому третье значение наибольшее.
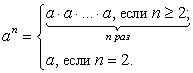
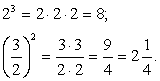

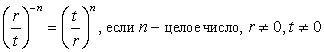 .
.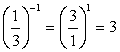 .
.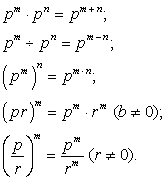
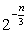 ;
;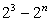 ;
;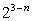 ;
;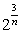 .
.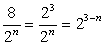 .
. 
