Московская финансово-промышленная академия

 

 

 

 

 

 

Н.Н. Прокимнов

 

 

 

 

Практикум по курсу
«Теория систем и системный анализ»

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Москва, 2009
Содержание

 

Введение. 3

 

1.    Экспертное оценивание. 3

 

2.    Метод анализа иерархий. 18

 

3.    Количественное оценивание сложных систем. 33

 

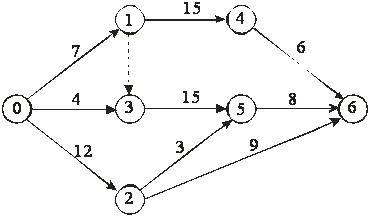
4.    Сетевое планирование и управление. 48

 

5.    Оценивание в условиях риска и неопределенности. 58

 

Литература. 76

 

Введение

 

Учебное пособие содержит описание лабораторных работ, перечни контрольных вопросов, подборку задач и дополнительных заданий к лабораторным работам по основным разделам курса “Теория систем и системный анализ”.

Описание содержания и порядка выполнения практической работы предваряется основными сведениями из теории  систем по основной теме занятия. Вслед за описанием порядка выполнения и требований к составу и форме представления результатов работы дается перечень контрольных вопросов.

Содержание заданий на выполнение работ лабораторного практикума предполагает знакомство с основными понятиями теории вероятностей, теории графов, а также наличие базовых навыков работы с электронными таблицами (приложением Excel пакета Microsoft Office).

 

1.                Экспертное оценивание

 

1.1.         Цель работы:

Изучение методов экспертного оценивания сложных систем.

 

1.2.Теоретические сведения.

1.2.1. Понятие экспертизы.

Методы групповых экспертных оценок наиболее часто используются в практике оценивания сложных систем на качественном уровне ([1],[4]) и находят применение в самых различных предметных областях.

Совокупность опрашиваемых участников процесса называется референтной или экспертной группой, а для оцениваемых объектов принято использовать термин факторы.

Принятие решений с помощью экспертов обычно включает следующие этапы:

 

 

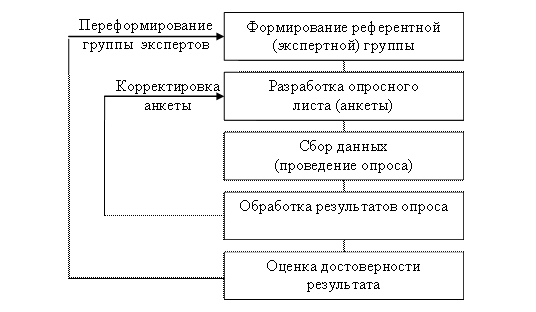
Качество результата и эффективность процесса экспертизы зависит во много от применяемых математических методов ее проведения.

 

1.2.2. Представление результатов экспертизы.

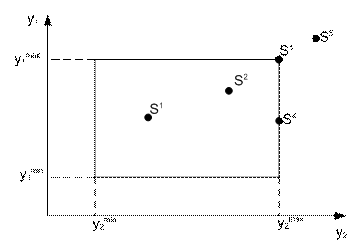
Результатом экспертизы является так называемая совокупность групповых предпочтений, к изображению которой имеются два альтернативных подхода (как и к изображению индивидуальных предпочтений):

-  ординальное (порядковое) предпочтение — здесь объекты упорядочиваются по рангу или месту в общем ряду совокупности. Ранг — это число i= 1, ..., n, где n — общая численность факторов;

-  кардинальное (числовое) представление. Здесь каждому фактору ставится в соответствие вес или число wi, вся группа оцениваемых факторов описывается вектором

 

,   обычно 

 

Рассмотрим данные методы сбора для общей ситуации: наличия п объектов а1, а2,... an  (или факторов Ф1, Ф2, ..., Фn) и т экспертов Э1, ..., Э2, ..., Эm.

В практике ранжирования объектов, между которыми допускаются отношения как строгого порядка, так и эквивалентности, числовое представление выбирается следующим образом.

Наиболее предпочтительному объекту присваивается ранг, равный единице, второму по предпочтительности - ранг, равный двум, и т.д. Для эквивалентных объектов удобно с точки зрения технологии последующей обработки экспертных оценок назначать одинаковые ранги, равные среднеарифметическому значению рангов, присваиваемых Одинаковым объектам. Такие ранги называют связанными рангами. Например, в случае, если неразличимыми являются факторы Ф 3 , Ф 4 , Ф 5, то каждому из них присваивается ранг   (3+4+5) / 3 = 4. Связанные ранги могут оказаться дробными числами. Удобство использования связанных рангов заключается в том, что сумма рангов n объектов равна сумме натуральных чисел от единицы до n. Существенно, что сумма всех рангов для данного эксперта должна быть постоянной и равняться 1 + 2 + ... + n = .

В отличие от ранжирования, в котором осуществляется упорядочение всех объектов, парное сравнение объектов является более простой задачей. При сравнении пары объектов возможно либо отношение строгого порядка, либо отношение эквивалентности. Каждый эксперт записывает свой результат в формат матрицы, например, для пяти факторов

 

 

Ф1

Ф2

Ф3

Ф4

Ф5

Ф1

1

2

2

2

0

Ф2

0

1

1

1

0

Ф3

0

0

1

1

0

Ф4

0

0

1

1

0

Ф5

2

2

2

2

1

 

где  каждый элемент

 

 

1.2.3. Обработка результатов экспертизы.

Основным результатом обработки результатов экспертизы является вектор весов факторов:

 

 

который строится в два этапа.

1)   Построение системы векторов или матрицы Х = (хij)

 

 

Это матрица индивидуальных весов, где j-й столбец описывает веса, приписанные j-м экспертом j=1...m, по всем  n факторам, причем

 

 для j=1,…m

 

2)   Построение групповых весов (при использовании метода ранжирования обычно получают также групповые ранги).

Если мнения экспертов представлены в виде матриц парных сравнений, матрица нормированных весов Х на базе последовательности матриц В: {В', ..., Вj, ..., Вm}. Вначале определяется сумма в каждой строке матрицы В, дающая вектор-столбец β:

 

 

где  — сумма элементов по i-й строке;

 

 =  (bik —элемент матрицы В = Вj).

 

Затем осуществляется нормирование элементов вектора, приводящее к весам:

 

 

Причем

 

 

В случае, если используется метод ранжирования, матрица строится в два этапа:

1) Строится матрица преобразованных рангов

 

 

элементы которой Rij вычисляются по следующему правилу:

 

 

 

2) Строится матрица нормированных весов Х= (хij), где

 

 

Поскольку

 

 для j=1,2,…m

 

1.2.4. Построение центроида.

Центроид (групповое мнение) находится где-то внутри области, ограниченной крайними мнениями», а фактическое его местонахождение зависит от выбора меры или критерия расстояния между векторами х1 ... хm.

Классической мерой близости является квадрат отклонения. Поэтому наиболее распространенный метод построения центроида есть нахождение вектора-столбца w, такого, что

 

   

 

Известно, что это выполняется тогда и только тогда, когда

 

 

т. е.  является средним арифметическим оценок варианта ai экспертами Э1, ..., Эj, ..., Эm.

При использовании метода ранжирования в качестве результата часто приводят групповые ранги.

 

1.2.5. Анализ результатов.

На этапе анализа пытаются оценить, можно ли доверять полученным результатам. А именно, насколько плотно расположенными друг к другу оказались мнения экспертов.

Традиционной мерой оценки плотности области мнений для случая голосования методом ранжирования является коэффициент конкордации Кендалла (W).

Коэффициент конкордации W изменяется от 1 до приблизительно нуля, при этом он равен 1, если все ранжировки комонотонны, т. е. совпадают, и наоборот, равен нулю, если они образуют все возможные перестановки, т. е. они все контрамонотонны (это в точности возможно только при п=т).

Строится W следующим образом.

Вначале в каждой строке матрицы рангов R={Rj) вычисляется сумма элементов (рангов):

 

 

По матрице R в целом вычисляется среднее значение R;.

 

 

Далее определяется сумма s  квадратов отклонений значений в строке матрицы R от

 

 

Коэффициент конкордации W вычисляется на основе выражения:

 

 

Для случая наличия связанных рангов W приобретает более сложный вид, поэтому данное выражение дает только приближенное значение.

 

1.3.Содержание работы.

Вариант работы определяется порядковым номером в списке группы.

Работа выполняется с помощью табличного редактора Microsoft Excel.

 

1.3.1. Парные оценки.

Для данных экспертизы, представленных в виде матриц парных оценок, требуется:

1)  построить групповое мнение (центроид);  

2)  определить коэффициент конкордации.

Перечень вариантов приведен в разделе 1.6.1.

 

1.3.2. Ранжирование.

Для данных экспертизы, представленных в виде матрицы рангов, требуется:

1)   построить групповое мнение (центроид);

2)   определить коэффициент конкордации.

Перечень вариантов приведен в разделе 0.

 

1.4.         Отчет по работе.

Отчет по работе должен включать исходные данные и результаты.

1) Расчеты и результаты для заданий по пп. 1.3.1, 1.3.2 должны быть размещены на отдельных листах с именами 1 и 2 соответственно.

2) Исходные и промежуточные данные по каждому эксперту (п. 1.3.1) должны располагаться по левой стороне листа друг под другом в последовательности:

 

А - матрица парных сравнений 

Б - матрица сумм элементов строк

В - вектор-столбец нормированных весов

Г - вектор-столбцов рангов

å - контрольная сумма элементов столбца.

 

3)  Результаты

Групповое мнение:

 

 

А - матрица весов,

Б - вектор-столбец группового мнения (веса),

В - вектор-столбец группового мнения (ранги),

å - контрольная сумма элементов столбца.

Коэффициент конкордации:

 

 

А - матрица рангов,

Б - суммы элементов строк А,

В – сумма квадратов разностей элементов Б и среднего по матрице А,

Г – коэффициент конкордации,

å -контрольная сумма элементов столбца.

Точность вычислений и результата – два десятичных знака.

 

1.5.  Контрольные вопросы.

1) Что такое экспертиза?

2) Из каких основных шагов состоит процесс проведения экспертного оценивания?

3) Экспертное оценивание относится к качественным или количественным методам оценивания?

4) Какие методы сбора данных экспертизы являются наиболее употребительными?

5) Какие сложности могут возникать при использовании сбора данных на основе метода парных оценок?

6) Каким образом определяется групповое мнение на основании собранных данных экспертизы?

7) Как определяется и как рассчитывается коэффициент конкордации?

 

1.6.         Варианты.

1.6.1. Метод парных сравнений

 

Номера матриц с результатами экспертизы

 

№

Номера матриц

Э1

Э2

Э3

Э4

Э5

1

11

13

14

15

31

2

11

12

13

14

14

3

11

14

16

17

18

4

16

17

19

20

22

5

20

21

22

23

24

6

24

25

26

27

29

7

12

13

14

15

18

8

14

28

29

30

31

9

17

32

33

34

37

10

14

17

32

35

37

11

15

20

32

14

36

12

15

22

36

37

16

13

17

18

20

21

23

14

19

20

21

22

25

15

22

27

32

34

36

16

16

21

31

35

22

17

29

23

24

25

28

18

11

20

23

24

28

19

16

19

21

23

25

20

18

19

24

25

26

21

25

27

30

32

34

22

26

28

29

33

35

23

11

12

17

18

20

24

13

14

15

18

20

 

Матрицы с результатами экспертизы

 

1

1

2

2

2

2

 

0

1

0

2

2

0

2

1

2

2

0

0

0

1

2

0

0

0

0

1

2

1

2

2

2

2

 

0

1

2

2

2

0

0

1

0

2

0

0

2

1

2

0

0

0

0

1

3

1

0

1

1

2

 

2

1

2

2

2

1

0

1

1

2

1

0

1

1

2

0

0

0

0

1

4

1

0

2

2

2

 

2

1

2

2

0

0

0

1

1

2

0

0

1

1

0

0

2

0

2

1

5

1

1

0

2

2

 

1

1

0

2

0

2

2

1

1

2

0

0

1

1

0

0

2

0

2

1

6

1

1

2

2

2

 

1

1

2

2

1

0

0

1

2

2

0

0

0

1

0

0

1

0

2

1

7

1

0

2

2

2

 

2

1

2

2

1

0

0

1

0

2

0

0

2

1

2

0

1

0

0

1

8

1

0

2

2

2

 

2

1

2

2

1

0

0

1

2

2

0

0

0

1

2

0

1

0

0

1

9

1

0

1

1

2

 

2

1

2

2

1

1

0

1

2

2

1

0

0

1

0

0

1

0

2

1

 

11

1

2

0

2

2

2

 

0

1

0

2

2

2

2

2

1

2

2

2

0

0

0

1

0

2

0

0

0

2

1

2

0

0

0

0

0

1

12

1

1

1

2

0

2

 

1

1

2

2

1

2

1

0

1

1

0

2

0

0

1

1

0

0

2

1

2

2

1

2

0

0

0

2

0

1

13

1

1

1

2

1

1

 

1

1

2

2

2

1

1

0

1

0

0

0

0

0

2

1

0

1

1

0

2

2

1

1

1

1

2

1

1

1

14

1

1

1

2

2

1

 

1

1

2

2

2

1

1

0

1

1

0

2

0

0

1

1

0

2

0

0

2

2

1

2

1

1

0

0

0

1

15

1

1

1

2

2

2

 

1

1

2

2

2

2

1

0

1

1

0

2

0

0

1

1

2

2

0

0

2

0

1

2

0

0

0

0

0

1

16

1

1

0

2

2

2

 

1

1

1

2

2

2

2

1

1

2

2

2

0

0

0

1

2

0

0

0

0

0

1

0

0

0

0

2

2

1

17

1

1

0

2

1

2

 

1

1

1

2

1

1

2

1

1

2

0

2

0

0

0

1

2

1

1

1

2

0

1

2

0

1

0

1

0

1

18

1

1

1

2

2

1

 

1

1

2

2

2

1

1

0

1

1

0

2

0

0

1

1

0

1

0

0

2

2

1

2

1

1

0

1

0

1

19

1

0

0

2

0

2

 

2

1

0

2

0

1

2

2

1

1

2

2

0

0

1

1

0

2

2

2

0

2

1

2

0

1

0

0

0

1

20

1

0

2

2

1

2

 

2

1

0

2

0

1

0

2

1

2

0

2

0

0

0

1

0

0

1

2

2

2

1

2

0

1

0

2

0

1

21

1

0

2

0

1

2

 

2

1

0

2

0

1

0

2

1

2

2

2

2

0

0

1

0

1

1

2

0

2

1

2

0

1

0

1

0

1

22

1

1

0

2

2

2

 

1

1

1

2

2

2

2

1

1

2

2

2

0

0

0

1

0

0

0

0

0

2

1

0

0

0

0

2

2

1

23

1

2

0

2

1

2

 

0

1

1

2

0

2

2

1

1

2

0

2

0

0

0

1

0

2

1

2

2

2

1

2

0

0

0

0

0

1

24

1

0

2

0

1

2

 

2

1

0

2

0

1

0

2

1

2

0

2

2

0

0

1

0

1

1

2

2

2

1

2

0

1

0

1

0

1

25

1

1

0

2

2

2

 

1

1

0

2

0

1

2

2

1

2

2

2

0

0

0

1

0

0

0

2

0

2

1

2

0

1

0

2

0

1

26

1

1

1

2

1

2

 

1

1

0

2

0

1

1

2

1

2

0

2

0

0

0

1

0

2

1

2

2

2

1

2

0

1

0

0

0

1

27

1

1

0

2

1

2

 

1

1

0

2

0

1

2

2

1

2

0

2

0

0

0

1

0

1

1

2

2

2

1

2

0

1

0

1

0

1

28

1

0

2

2

1

1

 

2

1

1

2

1

1

0

1

1

0

0

0

0

0

2

1

0

1

1

1

2

2

1

2

1

1

2

1

0

1

29

1

2

2

2

0

1

 

0

1

2

2

1

1

0

0

1

2

1

2

0

0

0

1

0

1

2

1

1

2

1

2

1

1

0

1

0

1

30

1

0

2

2

0

1

 

2

1

2

2

2

1

0

0

1

1

1

2

0

0

1

1

0

1

2

0

1

2

1

0

1

1

0

1

2

1

31

1

1

1

2

2

1

 

1

1

2

2

2

1

1

0

1

1

0

2

0

0

1

1

2

2

0

0

2

0

1

2

1

1

0

0

0

1

32

1

2

0

2

2

2

 

0

1

0

2

2

2

2

2

1

2

2

2

0

0

0

1

0

0

0

0

0

2

1

2

0

0

0

2

0

1

33

1

2

0

1

1

1

 

0

1

0

2

2

1

2

2

1

2

2

1

1

0

0

1

0

2

1

0

0

2

1

0

1

1

1

0

2

1

34

1

1

1

2

2

1

 

1

1

2

2

2

1

1

0

1

2

0

2

0

0

0

1

1

2

0

0

2

1

1

2

1

1

0

0

0

1

35

1

1

0

2

2

2

 

1

1

1

2

2

2

2

1

1

2

2

2

0

0

0

1

1

0

0

0

0

1

1

0

0

0

0

2

2

1

36

1

1

2

2

2

2

 

1

1

0

2

1

2

0

2

1

2

0

2

0

0

0

1

1

2

0

1

2

1

1

2

0

0

0

0

0

1

37

1

2

0

2

2

2

 

0

1

0

2

2

2

2

2

1

2

2

1

0

0

0

1

1

1

0

0

0

1

1

1

0

0

1

1

1

1

 

1.6.2.Метод ранжирования

 

Результаты экспертизы (матрицы рангов)

 

1.

Э1

Э2

Э3

Э4

Э5

Ф1

3,0

2,0

2,0

2,0

2,0

Ф2

1,0

1,0

1,0

1,0

4,0

Ф3

6,0

4,0

4,5

4,0

3,0

Ф4

5,0

5,0

3,0

6,0

6,0

Ф5

3,0

3,0

4,5

3,0

1,0

Ф6

3,0

6,0

6,0

5,0

5,0

2.

Э1

Э2

Э3

Э4

Э5

Ф1

2,0

3,0

2,0

2,0

2,0

Ф2

3,0

1,0

1,0

1,0

1,0

Ф3

1,0

6,0

4,0

4,5

4,5

Ф4

5,0

5,0

5,0

3,0

3,0

Ф5

4,0

3,0

3,0

4,5

4,5

Ф6

6,0

3,0

6,0

6,0

6,0

3.

Э1

Э2

Э3

Э4

Э5

Ф1

2,0

3,0

3,0

2,0

2,0

Ф2

3,0

2,0

1,0

1,0

1,0

Ф3

1,0

4,0

6,0

4,0

4,0

Ф4

5,0

6,0

5,0

5,0

5,0

Ф5

4,0

1,0

3,0

3,0

3,0

Ф6

6,0

5,0

3,0

6,0

6,0

4.

Э1

Э2

Э3

Э4

Э5

Ф1

2,0

2,0

3,0

3,0

2,0

Ф2

3,0

1,0

2,0

3,0

1,0

Ф3

1,0

4,0

1,0

1,0

4,0

Ф4

5,0

5,0

5,0

5,0

6,0

Ф5

4,0

3,0

6,0

3,0

3,0

Ф6

6,0

6,0

4,0

6,0

5,0

5.

Э1

Э2

Э3

Э4

Э5

Ф1

3,0

3,0

4,0

2,0

3,0

Ф2

2,0

3,0

3,0

4,0

2,0

Ф3

1,0

1,0

1,0

3,0

1,0

Ф4

5,0

5,0

5,0

6,0

6,0

Ф5

6,0

3,0

2,0

1,0

5,0

Ф6

4,0

6,0

6,0

5,0

4,0

6.

Э1

Э2

Э3

Э4

Э5

Ф1

2,0

3,5

3,0

2,5

3,5

Ф2

4,0

3,5

2,0

4,0

3,5

Ф3

3,0

1,0

1,0

2,5

2,0

Ф4

6,0

5,0

6,0

5,0

5,0

Ф5

1,0

2,0

5,0

1,0

1,0

Ф6

5,0

6,0

4,0

6,0

6,0

7.

Э1

Э2

Э3

Э4

Э5

Ф1

3,5

2,0

2,5

3,0

2,0

Ф2

3,5

4,0

4,0

4,0

3,0

Ф3

2,0

1,0

2,5

2,0

4,0

Ф4

5,0

6,0

5,0

6,0

6,0

Ф5

1,0

3,0

1,0

1,0

1,0

Ф6

6,0

5,0

6,0

5,0

5,0

8.

Э1

Э2

Э3

Э4

Э5

Ф1

3,0

3,0

2,0

2,0

2,0

Ф2

2,0

1,0

1,0

1,0

1,0

Ф3

4,0

6,0

4,0

4,5

4,0

Ф4

6,0

5,0

5,0

3,0

6,0

Ф5

1,0

3,0

3,0

4,5

3,0

Ф6

5,0

3,0

6,0

6,0

5,0

9.

Э1

Э2

Э3

Э4

Э5

Ф1

2,0

3,0

2,0

3,0

2,0

Ф2

1,0

2,0

3,0

1,0

1,0

Ф3

4,0

6,0

4,0

5,0

4,5

Ф4

5,0

5,0

6,0

6,0

3,0

Ф5

3,0

1,0

1,0

3,0

4,5

Ф6

6,0

4,0

5,0

3,0

6,0

10.

Э1

Э2

Э3

Э4

Э5

Ф1

3,0

2,0

3,0

2

2,0

Ф2

3,0

3,0

3,0

1

3,0

Ф3

1,0

1,0

1,0

3,5

1,0

Ф4

5,0

6,0

5,5

5

5,5

Ф5

3,0

4,0

5,5

3,5

5,5

Ф6

6,0

5,0

3,0

6

4,0

11.

Э1

Э2

Э3

Э4

Э5

Ф1

2,0

3,0

2,0

3,0

2,0

Ф2

1,0

3,0

3,0

2,0

3,0

Ф3

4,0

1,0

1,0

1,0

1,0

Ф4

5,0

5,0

6,0

5,5

5,5

Ф5

3,0

3,0

4,0

5,5

5,5

Ф6

6,0

6,0

5,0

4,0

4,0

12.

Э1

Э2

Э3

Э4

Э5

Ф1

2,0

2,0

2,0

2,0

1,0

Ф2

1,0

4,0

3,0

1,0

3,0

Ф3

4,5

3,0

1,0

4,0

3,0

Ф4

3,0

6,0

6,0

5,0

5,0

Ф5

4,5

1,0

4,0

3,0

3,0

Ф6

6,0

5,0

5,0

6,0

6,0

13.

Э1

Э2

Э3

Э4

Э5

Ф1

2,0

3,0

1,0

2,0

3,0

Ф2

1,0

2,0

3,0

3,0

2,0

Ф3

4,5

1,0

3,0

1,0

1,0

Ф4

3,0

6,0

5,0

5,5

5,0

Ф5

4,5

5,0

3,0

5,5

6,0

Ф6

6,0

4,0

6,0

4,0

4,0

14.

Э1

Э2

Э3

Э4

Э5

Ф1

3,0

2,0

2,0

3,5

2,5

Ф2

3,0

1,0

4,0

3,5

4,0

Ф3

1,0

4,0

3,0

1,0

2,5

Ф4

5,0

6,0

6,0

5,0

5,0

Ф5

3,0

3,0

1,0

2,0

1,0

Ф6

6,0

5,0

5,0

6,0

6,0

15.

Э1

Э2

Э3

Э4

Э5

Ф1

4,0

2,0

3,5

3,0

2,0

Ф2

3,0

4,0

3,5

2,0

4,0

Ф3

1,0

3,0

1,0

1,0

1,0

Ф4

5,0

6,0

5,0

6,0

6,0

Ф5

2,0

1,0

2,0

5,0

3,0

Ф6

6,0

5,0

6,0

4,0

5,0

16.

Э1

Э2

Э3

Э4

Э5

Ф1

3,0

3,0

2,0

2,0

1,0

Ф2

2,0

4,0

3,0

1,0

3,0

Ф3

1,0

2,0

1,0

3,5

3,0

Ф4

6,0

6,0

6,0

5,0

5,0

Ф5

5,0

1,0

4,0

3,5

3,0

Ф6

4,0

5,0

5,0

6,0

6,0

17.

Э1

Э2

Э3

Э4

Э5

Ф1

3,0

3,5

2,0

3,0

3,0

Ф2

2,0

3,5

1,0

2,0

2,0

Ф3

1,0

1,0

4,5

1,0

1,0

Ф4

5,0

5,0

3,0

4,5

6,0

Ф5

6,0

2,0

4,5

4,5

5,0

Ф6

4,0

6,0

6,0

6,0

4,0

18.

Э1

Э2

Э3

Э4

Э5

Ф1

2,0

2,5

3,5

2,0

3,0

Ф2

3,0

4,0

3,5

4,0

2,0

Ф3

4,0

2,5

2,0

1,0

6,0

Ф4

6,0

5,0

5,0

6,0

5,0

Ф5

1,0

1,0

1,0

3,0

1,0

Ф6

5,0

6,0

6,0

5,0

4,0

19.

Э1

Э2

Э3

Э4

Э5

Ф1

2,0

2,0

2,5

3,5

3,0

Ф2

3,0

4,0

4,0

3,5

2,0

Ф3

1,0

3,0

2,5

2,0

6,0

Ф4

5,0

6,0

5,0

5,0

5,0

Ф5

4,0

1,0

1,0

1,0

1,0

Ф6

6,0

5,0

6,0

6,0

4,0

20.

Э1

Э2

Э3

Э4

Э5

Ф1

3,0

4,0

3,5

2,5

2,0

Ф2

2,0

3,0

3,5

4,0

4,0

Ф3

1,0

1,0

1,0

2,5

1,0

Ф4

5,0

5,0

5,0

5,0

6,0

Ф5

6,0

2,0

2,0

1,0

3,0

Ф6

4,0

6,0

6,0

6,0

5,0

21.

Э1

Э2

Э3

Э4

Э5

Ф1

2,0

4,0

3,5

2,0

2,5

Ф2

1,0

3,0

3,5

4,0

4,0

Ф3

4,0

1,0

2,0

1,0

2,5

Ф4

6,0

5,0

5,0

6,0

5,0

Ф5

3,0

2,0

1,0

3,0

1,0

Ф6

5,0

6,0

6,0

5,0

6,0

22.

Э1

Э2

Э3

Э4

Э5

Ф1

2,0

3,0

3,0

2,0

2,0

Ф2

4,0

4,0

1,0

3,0

1,0

Ф3

1,0

2,0

5,0

1,0

3,5

Ф4

6,0

6,0

6,0

6,0

5,0

Ф5

3,0

1,0

3,0

4,0

3,5

Ф6

5,0

5,0

3,0

5,0

6,0

23.

Э1

Э2

Э3

Э4

Э5

Ф1

2,5

3,0

2,0

3,0

3,0

Ф2

4,0

2,0

3,0

3,0

2,0

Ф3

2,5

6,0

4,0

1,0

1,0

Ф4

5,0

5,0

6,0

5,5

5,5

Ф5

1,0

1,0

1,0

5,5

5,5

Ф6

6,0

4,0

5,0

3,0

4,0

24.

Э1

Э2

Э3

Э4

Э5

Ф1

2,0

3,0

3,0

2,0

2,0

Ф2

3,0

2,0

3,0

1,0

4,0

Ф3

1,0

4,0

1,0

4,0

3,0

Ф4

5,0

6,0

5,0

6,0

6,0

Ф5

4,0

1,0

3,0

3,0

1,0

Ф6

6,0

5,0

6,0

5,0

5,0

 

2. Метод анализа иерархий

 

2.1.Цель работы:

Практическое изучение метода анализа иерархий.

 

2.2.Теоретические сведения

Метод анализа иерархий, разработанный и опубликованный в 1970 году американским математиком Саати [3], относится к классу критериальных. Он  получил очень широкое распространение и в настоящее время продолжает активно применяться - см., например, [6] (задача составления оптимального производственного плана нефтепереработки), [7] (задача оценки недвижимости).

На первом этапе применения метода  предусматривается структурирование проблемы в виде иерархии или сети. Иерархия строится с вершины (целей — с точки зрения управления), через промежуточные уровни (критерии, от которых зависят последующие уровни) к самому низкому уровню (который обычно является перечнем вариантов выбора).

Иерархия считается полной, если каждый элемент заданного уровня функционирует как критерий для всех элементов нижестоящего уровня. В противном случае иерархия — неполная. Нетрудно понять процесс определения весов в случае неполной иерархии, так как используются приоритеты соответствующего элемента, по отношению к которому производится оценка, т. е. иерархия может быть разделена на подиерархии, имеющие общим самый верхний элемент.

Для объяснения метода анализа иерархий рассмотрим пример, иллюстрирующий иерархическое представление задачи. Предположим, что перед нами стоит задача выбора автомобиля из совокупности, члены которой (модели автомобилей) обозначаются как А, Б, В и Г.

Определив на первом  (высшем)  уровне общую цель — «Автомобиль» - на втором уровне находятся пять факторов или критериев, уточняющих цель, и на третьем (нижнем) уровне находятся четыре автомобиля - кандидата, которые должны быть оценены по отношению к критериям второго уровня.

В качестве критериев, определяющих наш выбор, используются такие критерии:

1) Вместительность салона и багажника

2) Экономичность (расход горючего)

3) Ходовые качества

4) Дизайн

5) Стоимость

 

Следующим шагом метода после выполнения шага иерархического или сетевого воспроизведения проблемы производится установление приоритетов критериев и оценка каждого вариантов альтернативы по критериям. В методе анализа иерархий элементы задачи сравниваются попарно по отношению к их воздействию («весу», или «интенсивности») на общую для них характеристику. Проведем парные сравнения, приводящие к матричной форме. Сравнивая набор составляющих проблемы друг с другом, получаем следующую квадратную матрицу:

 

 

Очевидно, что эта матрица имеет свойства обратной симметричности, т. е.

 

 

где  индексы i и j относятся к строке  и столбцу соответственно.

Пусть А1, А2, Аз, ..., Аn — множество из n элементов и w1, w2 w3, ..., wn — соответственно их веса, или интенсивности. С использованием метода анализа иерархий вес, или интенсивность, каждого элемента сравниваются с весом, или интенсивностью, любого другого элемента множества по отношению к общему для них свойству или цели. Сравнение весов можно представить квадратной таблицей, в которой числа могут быть расположены следующим образом

 

 

Если w1, w2, w3 ..., wn неизвестны заранее, то попарные сравнения элементов производятся с использованием субъективных суждений, оцениваемых численно по некоторой шкале, а вслед за чем решается проблема нахождения компонент w.

Для фиксации результата сравнения пары альтернатив может использоваться, в частности, шкала, предложенная автором метода:

1 - равноценность

3 - умеренное превосходство

5 - сильное превосходство

7 - очень сильное превосходство

9 - высшее (крайнее) превосходство

 

Значения 2,4,6,8 используются для обозначения промежуточной между перечисленными значениями степени превосходства.

Если элемент i важнее элемента j, то в клетку заносится положительное целое (от 1 до 9); в противном случае — обратное число (дробь). Относительная важность любого элемента, сравниваемого с самим  собой, равна 1; поэтому диагональ матрицы (элементы от левого верхнего угла до нижнего правого) содержит только единицы. Симметричные клетки заполняются обратными величинами, т. е. если элемент А воспринимается как «слегка более важный» (3 на шкале) относительно элемента Б, то считаем, что элемент Б «слегка менее важен»  (1/3 на шкале) относительно элемента А.

Когда проблемы представлены иерархически, матрица составляется для сравнения относительной важности критериев на втором уровне по отношению к общей цели на первом уровне. Подобные матрицы должны быть построены для парных сравнений каждого варианта альтернативы на третьем уровне по отношению к критериям второго уровня. Матрица составляется, если записать сравниваемую цель (или критерий) вверху и перечислить сравниваемые элементы слева и сверху.

В примере потребуется построить шесть таких матриц.

Одна матрица создается для второго уровня иерархии, например,

 

 

Кр1

Кр2

Кр3

Кр4

Кр5

Кр1

1

5

3

7

6

Кр2

1/5

1

1/3

5

3

Кр3

1/3

3

1

6

3

Кр4

1/7

1/5

1/6

1

1/3

Кр5

1/6

1/3

1/3

3

1

 

и пять матриц — для третьего уровня, например,

 

Вместительность:

 

 

А

Б

В

Г

А

1

1

2

4

Б

1

1

4

3

В

1/2

1/4

1

3

Г

1/4

1/3

1/3

1

 

Экономичность:

 

 

А

Б

В

Г

А

1

3

5

7

Б

1/3

1

3

2

В

1/5

1/3

1

3

Г

1/7

1/2

1/3

1

 

Ходовые качества:

 

 

А

Б

В

Г

А

1

3

5

7

Б

1/3

1

3

2

В

1/5

1/3

1

3

Г

1/7

1/2

1/3

1

 

Дизайн:

 

 

А

Б

В

Г

А

1

2

4

8

Б

1/2

1

3

2

В

1/4

1/3

1

2

Г

1/8

1/2

1/2

1

 

Стоимость:

 

 

А

Б

В

Г

А

1

1

3

2

Б

1

1

1

2

В

1/3

1

1

1/2

Г

1/2

1/2

2

1

 

Сравниваемые попарно элементы — это возможные варианты выбора автомобиля. Сравнивается, насколько более желателен или хорош тот или иной автомобиль для удовлетворения каждого критерия второго уровня. Получаем пять матриц суждений размерностью 4х4, поскольку имеется пять критериев на втором уровне и четыре автомобиля, которые попарно сравниваются по каждому из критериев.

Из группы матриц парных сравнений формируется набор локальных приоритетов, которые выражают относительное влияние множества элементов на элемент примыкающего сверху уровня. Находим относительную силу, величину, ценность, желательность или вероятность каждого отдельного объекта через «решение» матриц, каждая из которых обладает обратносимметричными свойствами. Для этого нужно вычислить множество собственных векторов для каждой матрицы, а затем нормализовать результат к единице, получая тем самым вектор приоритетов. Вычисление собственных векторов заменяется более простым приближенным вычислением приоритетов каждого критерия в виде среднего геометрического. Для этого элементы в каждой строке перемножаются и из каждого произведения извлекается корень n-й степени, где n — число элементов (вариантов альтернативы). Полученный таким образом столбец чисел нормализуется делением каждого числа на сумму всех чисел. Таким образом, можно определить не только порядок приоритетов каждого отдельного элемента, но и величину его приоритета. Для нашего примера имеем:

 

 

Кр1

Кр2

Кр3

Кр4

Кр5

П

Ö

P

Кр1

1

5

3

7

6

630.00

3.63

0.50

Кр2

1/5

1

1/3

5

3

1.00

1.00

0.14

Кр3

1/3

3

1

6

3

18.00

1.78

0.25

Кр4

1/7

1/5

1/6

1

1/3

0.00

0.28

0.04

Кр5

1/6

1/3

1/3

3

1

0.06

0.56

0.08

 

Для матриц третьего уровня:

Вместительность:

 

 

А

Б

В

Г

П

Ö

X

А

1

1

2

4

8.00

1.68

0.36

Б

1

1

4

3

12.00

1.86

0.39

В

1/2

1/4

1

3

0.38

0.78

0.17

Г

1/4

1/3

1/3

1

0.03

0.41

0.09

Экономичность:

 

 

А

Б

В

Г

П

Ö

X

А

1

1

2

4

105.00

3.20

0.59

Б

1

1

4

3

2.00

1.19

0.22

В

1/2

1/4

1

3

0.20

0.67

0.12

Г

1/4

1/3

1/3

1

0.02

0.39

0.07

 

Ходовые качества:

 

 

А

Б

В

Г

П

Ö

X

А

1

1

2

4

189.00

3.71

0.60

Б

1

1

4

3

6.67

1.61

0.26

В

1/2

1/4

1

3

0.09

0.54

0.09

Г

1/4

1/3

1/3

1

0.01

0.31

0.05

 

Дизайн:

 

 

А

Б

В

Г

П

Ö

X

А

1

1

2

4

64.00

2.83

0.54

Б

1

1

4

3

3.00

1.32

0.25

В

1/2

1/4

1

3

0.17

0.64

0.12

Г

1/4

1/3

1/3

1

0.03

0.42

0.08

 

Стоимость:

 

 

А

Б

В

Г

П

Ö

X

А

1

1

3

2

6.00

1.57

0.37

Б

1

1

1

2

2.00

1.19

0.28

В

1/3

1

1

1/2

0.17

0.64

0.15

Г

1/2

1/2

2

1

0.50

0.84

0.20

 

Приоритеты синтезируются, начиная со второго уровня вниз. Локальные приоритеты перемножаются на приоритет соответствующего критерия на вышестоящем уровне и суммируются по каждому элементу в соответствии с критериями, на которые воздействует этот элемент. Это дает составной, или глобальный, приоритет того элемента, который затем используется для взвешивания локальных приоритетов элементов, сравниваемых по отношению к нему как, к критерию и расположенных уровнем ниже. Таким образом, для вычисления веса каждого варианта на третьем уровне необходимо найти сумму произведений веса каждого варианта по каждому критерию на величину приоритета данного критерия:

 

 

В условиях рассматриваемого примера имеем:

 

 

Весьма важным является так называемый индекс согласованности, который дает информацию о степени нарушения численной (кардинальной,  ) и транзитивной (порядковой) согласованности. Для улучшения согласованности рекомендуется произвести поиск дополнительной информации и пересмотр данных, использованных при построении шкалы. В других процедурах построения шкал отношения нет структурно порожденного индекса. Вместо традиционно используемых при построении ординальных шкал (  при использовании значений 0,1,2 для выражения предпочтений), как уже было отмечено выше, в матрицах парных сравнений метода используются обратные величины .

Индекс согласованности в каждой матрице и для всей иерархии может быть приближенно получен вычислениями вручную. Сначала суммируются элементы каждого столбца суждений, затем сумма первого столбца умножается на величину первой компоненты нормализованного вектора приоритетов, сумма второго столбца — на вторую компоненту и т. д. Затем полученные числа суммируются. Если обозначить эту сумму как , то для индекса согласованности (ИС) имеем:

 

,

 

где n — число сравниваемых элементов.

Теперь сравним эту величину с той, которая получилась бы при случайном выборе количественных суждений из шкалы 1/9, 1/8, 1/7,..., 1,2, ...,9. Средние согласованности для случайных матриц (CC - случайная согласованность) имеют такие значения:

 

n

1

2

3

4

5

6

7

8

9

10

СС

0

0

0,58

0,9

1,12

1,24

1,32

0,41

0,45

1,49

 

Отношение согласованности (ОС)  получим,  разделив ИС на число, соответствующее случайной согласованности матрицы того же порядка.

Для матрицы первого уровня данного примера имеем:

ИС=(5,29-5)/4=0,07

ОС=0,07/1,12=0,066

 

Для матриц третьего уровня:

ОС1=0,06

ОС2=0,04

ОС3=0,05

ОС4=0,03

ОС5=0,07

 

Приемлемой считается величина ОС порядка 10% или менее. В некоторых случаях можно допустить 20%, но не более. Если ОС выходит из этих пределов, то нужно повторно исследовать задачу и проверить свои суждения.

 

2.3.Задание

1. Откройте приложение  Microsoft Excel.

2. Подготовьте таблицу второго уровня

 

 

Кр1

Кр2

Кр3

…

…

П

√

P

Кр1

 

 

 

 

 

 

 

 

Кр2

 

 

 

 

 

 

 

 

Кр3

 

 

 

 

 

 

 

 

…

 

 

 

 

 

 

 

 

…

 

 

 

 

 

 

 

 

∑

 

 

 

 

 

 

 

 

λ

 

 

 

 

 

 

 

 

ИС

 

 

 

 

 

 

 

 

ОС

 

 

 

 

 

 

 

 

 

3. Заполните ячейки для парных сравнений исходными данными своего варианта.

 

Номер варианта соответствует порядковому номеру в списке группы.

4.  В ячейки для вычислений впишите нужные выражения.

П - произведение элементов строки

√  - значения корня произведения

P - приоритеты критериев

∑ - сумма элементов столбцов

λ  - значение

ИС - индекс согласованности

ОС – общая согласованность

 

5.  Подготовьте таблицы третьего уровня:

 

 

А

Б

В

Г

П

Ö

X

 А

 

 

 

 

 

 

 

 Б

 

 

 

 

 

 

 

 В

 

 

 

 

 

 

 

 Г

 

 

 

 

 

 

 

 ∑

 

 

 

 

 

 

 

 λ

 

 

 

 

 

 

 

 ИС

 

 

 

 

 

 

 

 ОС

 

 

 

 

 

 

 

 

6. Заполните ячейки таблиц исходными данными своего варианта.

7. В ячейки для вычислений  П, Ö,  X, ∑, λ, ИС, ОС впишите нужные выражения.

8. Запишите внизу листа выражения для вычисления веса каждого варианта.

 

2.4.Отчет по работе.

Отчет по работе должен включать заполненные таблицы, описанные в предыдущем разделе. Ниже приводятся образцы оформления.

Таблица второго уровня:

 

 

Кр1

Кр2

Кр3

Кр4

Кр5

П

√

Р

 

Кр1

1

5

3

7

6

630,00

3,63

0,50

 

Кр2

1/5

1

1/3

5

3

1,00

1,00

0,14

 

Кр3

1/3

3

1

6

3

18,00

1,78

0,25

 

Кр4

1/7

1/5

1/6

1

1/3

0,00

0,28

0,04

 

Кр5

1/6

1/3

1/3

3

1

0,06

0,56

0,08

 

∑

1,84

9,53

4,83

22,00

13,33

 

7,25

1,00

 

λ

0,92

1,32

1,19

0,84

1,03

 

 

 

5,29

ИС

 

 

 

 

 

 

 

 

0,07

ОС

 

 

 

 

 

 

 

 

0,066

 

Таблица третьего уровня:

 

 

А

Б

В

Г

П

√

Х

 

А

1

1

2

4

8,00

1,68

0,36

 

Б

1

1

4

3

12,00

1,86

0,39

 

В

1/2

1/4

1

3

0,38

0,78

0,17

 

Г

1/4

1/3

1/3

1

0,03

0,41

0,09

 

∑

2,75

2,58

7,33

11,00

 

4,73

1,00

 

λ

0,98

1,02

1,21

0,95

 

 

 

4,15

ИС

 

 

 

 

 

 

 

0,05

ОС

 

 

 

 

 

 

 

0,061

 

Результат:

 

А

0,46 

Б

0,32 

В

0,14 

Г

0,08 

 

1,00 

 

2.5.Контрольные вопросы.

1) В чем состоит основная идея метода анализа иерархий?

2) Каким образом представляются результаты суждений на каждом уровне иерархии?

3) Какая шкала суждений используется для составления матриц парных сравнений?

4) Какими свойствами должна обладать каждая матрица парных сравнений?

5) Как вычисляются приоритеты на каждом уровне?

6) Какие могут встречаться нарушения согласованности матрицы суждений?

7) Чем характеризуется качество суждений на каждом уровне?

8) Как считается величина общей согласованности таблицы суждений?

9) Как вычисляются веса вариантов на нижнем уровне иерархии?

 

2.6.         Варианты.

Варианты матриц

 

№

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

Уровень 2

1

2

3

4

5

6

7

8

1

2

3

4

5

6

7

8

1

2

3

4

5

6

7

8

Уровень 3

1

2

3

1

2

3

1

2

3

1

2

3

1

2

3

1

2

3

1

2

3

1

2

3

 

Уровень 2 - матрицы парных сравнений критериев

 

1

Кр1

Кр2

Кр3

Кр4

Кр5

Кр6

Кр1

1

3

4

1/2

5

2

Кр2

1/3

1

2

1/2

1

1

Кр3

1/4

1/2

1

1/2

1

1/2

Кр4

2

2

2

1

3

1

Кр5

1/5

1

1

1/3

1

1/3

Кр6

1/2

1

2

1

3

1

 

 

 

 

 

 

 

2

Кр1

Кр2

Кр3

Кр4

Кр5

Кр6

Кр1

1

2

1/2

2

3

2

Кр2

1/2

1

1

3

2

1

Кр3

2

1

1

2

1

1

Кр4

1/2

1/3

1/2

1

2

1

Кр5

1/3

1/2

1

1/2

1

1/2

Кр6

1/2

1

1

1

2

1

 

 

 

 

 

 

 

3

Кр1

Кр2

Кр3

Кр4

Кр5

Кр6

Кр1

1

2

5

1/2

1

2

Кр2

1/2

1

2

1/5

1/2

1

Кр3

1/5

1/2

1

1/9

1/3

1

Кр4

2

5

9

1

1

2

Кр5

1

2

3

1

1

2

Кр6

1/2

1

1

1/2

1/2

1

 

 

 

 

 

 

 

4

Кр1

Кр2

Кр3

Кр4

Кр5

Кр6

Кр1

1

2

3

1/4

1/2

2

Кр2

1/2

1

2

1/2

1/3

1/2

Кр3

1/3

1/2

1

1/7

1/5

1/2

Кр4

4

2

7

1

2

5

Кр5

2

3

5

1/2

1

3

Кр6

1/2

2

2

1/5

1/3

1

 

 

 

 

 

 

 

5

Кр1

Кр2

Кр3

Кр4

Кр5

Кр6

Кр1

1

1/2

3

2

1/5

5

Кр2

2

1

5

4

1/2

9

Кр3

1/3

1/5

1

1/2

1/9

2

Кр4

1/2

1/4

2

1

1/7

1/2

Кр5

5

2

9

7

1

9

Кр6

1/5

1/9

1/2

2

1/9

1

 

 

 

 

 

 

 

 6

Кр1

Кр2

Кр3

Кр4

Кр5

Кр6

Кр1

1

1/2

3

5

1

1/5

Кр2

2

1

6

5

3

1

Кр3

1/3

1/6

1

2

2

1/7

Кр4

1/5

1/5

1/2

1

1/3

1/9

Кр5

1

1/3

1/2

3

1

1/3

Кр6

5

1

7

9

3

1

 

 

 

 

 

 

 

 7

Кр1

Кр2

Кр3

Кр4

Кр5

Кр6

Кр1

1

3

1/2

1/5

2

4

Кр2

1/3

1

1/5

1/7

2

1

Кр3

2

5

1

1/3

5

7

Кр4

5

7

3

1

7

9

Кр5

1/2

1/2

1/5

1/7

1

3

Кр6

1/4

1

1/7

1/9

1/3

1

 

 

 

 

 

 

 

 8

Кр1

Кр2

Кр3

Кр4

Кр5

Кр6

Кр1

1

5

1/3

3

1/5

2

Кр2

1/5

1

1/7

1/3

1/9

1/2

Кр3

3

7

1

7

1/2

7

Кр4

1/3

3

1/7

1

1/9

1/2

Кр5

5

9

2

9

1

5

Кр6

1/2

2

1/7

2

1/5

1

 

Уровень 3 - матрицы парных сравнений объектов

Вариант 1

1

А

Б

В

А

1

5

7

Б

1/5

1

2

В

1/7

1/2

1

2

А

Б

В

А

1

4

1/4

Б

1/4

1

1/7

В

4

7

1

3

А

Б

В

А

1

4

5

Б

1/4

1

2

В

1/5

1/2

1

4

А

Б

В

А

1

1

1/2

Б

1

1

1/2

В

2

2

1

5

А

Б

В

А

1

4

3

Б

1/4

1

1/3

В

1/3

3

1

6

А

Б

В

А

1

4

2

Б

1/4

1

1/2

В

1/2

2

1

Вариант 2

1

А

Б

В

А

1

1/2

3

Б

2

1

3

В

1/3

1/3

1

2

А

Б

В

А

1

1

1/5

Б

1

1

1/8

В

5

8

1

3

А

Б

В

А

1

1/2

1/2

Б

2

1

2

В

2

1/2

1

4

А

Б

В

А

1

1/2

1

Б

2

1

3

В

1

1/3

1

5

А

Б

В

А

1

1

2

Б

1

1

3

В

1/2

1/3

1

6

А

Б

В

А

1

1/2

2

Б

2

1

2

В

1/2

1/2

1

 

Вариант 3

1

А

Б

В

А

1

1/2

1/3

Б

2

1

1/2

В

3

2

1

2

А

Б

В

А

1

2

1/2

Б

1/2

1

1/2

В

2

2

1

3

А

Б

В

А

1

2

3

Б

1/2

1

2

В

1/3

1/2

1

4

А

Б

В

А

1

1

1/3

Б

1

1

1/2

В

3

2

1

5

А

Б

В

А

1

2

1/2

Б

1/2

1

1/3

В

2

3

1

6

А

Б

В

А

1

1/2

1/5

Б

2

1

1/5

В

5

5

1

3. Количественное оценивание сложных систем.

3.1.         Цель работы:

Изучение:

1) использования частных и обобщенных показателей сложных систем;

2) критериев оценивания сложных систем;

3) выбора существенного множества альтернатив;

4) методов свертки частных показателей.

 

3.2.Теоретические сведения.

Каждое i-ое качество j-ой системы, i= 1,..., п; j = 1,..., т, может быть описано с помощью некоторой переменной  отображающей определенное свойство системы, значение которой характеризует меру этого качества. Эта мера называется показателем свойства или частным показателем качества системы. Каждый показатель yi может принимать значения из множества (области) допустимых значений .

Обобщенным показателем качества j-ой системы называется вектор , компонентами которого являются показатели отдельных системных свойств. Размерность этого вектора определяется числом существенных свойств системы (обратим внимание на то, что обобщенным показателем качества является именно вектор, а не простое множество частных показателей, поскольку между отдельными свойствами могут существовать связи, которые в рамках теории множеств описать весьма сложно).

Частные показатели имеют различную физическую природу и в соответствии с этим различную размерность. Поэтому при переходе к обобщенному показателю качества следует оперировать не с самими показателями, а с их нормированными значениями, обеспечивающими приведение показателей к одному масштабу, что необходимо для их сопоставления.

Задача нормировки решается, как правило, введением относительных безразмерных показателей, представляющих собой отношение измеренного частного показателя к некоторой нормирующей величине, измеряемой в тех же единицах, что и сам показатель

 

 

где  - некоторое «идеальное» значение i-го показателя.

Выбор нормирующего делителя для перевода частных показателей в безразмерную форму в значительной мере носит субъективный характер и должен обосновываться в каждом конкретном случае.

Возможны несколько подходов к выбору нормирующего делителя, в частности, следующие.

1)   может задаваться ЛПР. Такой способ задания означает, что значение  следует воспринимать как образцовое.

2)  Можно положить .

3)  В качестве  может быть взята разность между максимальным и минимальным допустимыми значениями частного показателя.

 

Требуемое качество системы задается правилами (условиями), которым должны удовлетворять показатели существенных свойств, а проверка их выполнения называется оцениванием качества системы. Таким образом, критерий качества есть показатель существенных свойств системы и правило его оценивания.

Все критерии в общем случае могут принадлежать одному из трех классов.

Критерий пригодности.

Согласно этому критерию j-ая система считается пригодной, если значения всех частных показателей  этой системы принадлежат области допустимых значений частных показателей.

 

Критерий оптимальности.

Согласно этому критерию j-ая система считается оптимальной по i-му показателю качества, если все значения частных показателей качества  принадлежат допустимой области и существует хотя бы один частный показатель качества , по которому достигается оптимум.

 

Критерий превосходства.

Согласно этому критерию j-ая система считается превосходной, если все значения частных показателей качества  принадлежат допустимой области и система оптимальна по всем показателям.

Иллюстрация приведенных формулировок приведена на

Рис. 3‑2 где по свойствам ух и у2 сравниваются характеристики пяти систем {S1, S2, S3, S4, S5},

 

 

Рис. 3‑1. Примеры критериев оценивания

 

имеющие допустимые области адекватности значений  у1 и у2, для которых оптимальные значения определены как  и  соответственно.

Из рисунка  видно, что системы S1, S2, S3, S4 пригодны по показателям у1 и у2. Система S5 не является пригодной.

Системы S3, S4 оптимальны по показателю у2.

Система S3 является превосходной.

Оценка сложных систем в условиях определенности на основе методов векторной оптимизации проводится в три этапа.

На первом этапе с использованием системного анализа определяются частные показатели и критерии эффективности.

На втором этапе находится множество Парето и формулируется задача многокритериальной оптимизации.

На третьем этапе задача решается путем скаляризации критериев с устранением многокритериальности.

Множество Парето определяется как подмножество А* множества альтернатив А. Множество А* (переговорное множество, множество компромиссов) включает альтернативы, которые всегда более предпочтительны по сравнению с любой альтернативой из множества А\А*. При этом любые две альтернативы из множества Парето по предпочтению несравнимы. Альтернативы  и  называются несравнимыми, если альтернатива  превосходит альтернативу  по одним критериям, а альтернатива  превосходит альтернативу  по другим. Выражение К(а*) > К(а) означает, что

 

 

и хотя бы одно из этих неравенств является строгим.

Понятие множества Парето можно пояснить на примере. Пусть имеем задачу оптимизации по двум критериям ,  где  и  - показатели свойств системы (параметры), значения которых можно выбирать. Целью является выбор оптимальных (в данном случае минимальных) значений параметров. Если изобразить множество критериев в виде многоугольника (

Рис. 3‑2):

 

 

Рис. 3‑2. Множество Парето

 

и рассмотреть пару точек  и  как показано на рисунке, то легко заметить, что для этих точек справедливо:

 

 

т.е., точка  является более предпочтительной по отношению к точке . Поэтому оставлять для рассмотрения точку  не имеет смысла.

Продолжая рассмотрение других точек области многоугольника, придем к тому, что для выбора остаются только точки стороны AE. Для каждой пары этих точек предпочтение по одному показателю сопровождается ухудшением по другому. 

Методы, основанные на свертке векторного критерия в скалярный, предполагают переход к решению задачи

 

 

где  - скалярный критерий, представляющий собой некоторую функцию от значений компонентов векторного критерия:

 

 

Основной проблемой этого подхода является построение функции f, называемой сверткой. Свертка производится в несколько этапов.

 

Обоснование допустимости свертки.

Требует подтверждения, что рассматриваемые показатели эффективности являются однородными. Известно, что показатели эффективности разделяются на три группы: показатели результативности, ресурсоемкости и оперативности. В общем случае разрешается свертка показателей, входящих в обобщенный показатель для каждой группы отдельно. Свертка показателей разных групп может привести к потере физического смысла такого критерия.

 

Нормализация критериев.

Проводится аналогично нормировке показателей.

 

Учет приоритетов критериев.

Осуществляется в большинстве методов свертывания путем задания вектора коэффициентов важности критериев l:

 

.

 

где  - коэффициент важности критерия , обычно совпадающий с коэффициентом значимости частного показателя качества.

Определение коэффициентов важности критериев, как и в случае с показателями, сталкивается с серьезными трудностями и сводится либо к использованию формальных процедур, либо к применению экспертных оценок.

В результате нормализации и учета приоритетов критериев вместо исходной векторной оценки К(а) альтернативы а образуется новая векторная оценка

 

 

где  - нормированный критерий, он находится аналогично нормированному показателю. Именно эта полученная векторная оценка подлежит преобразованию с использованием функции свертки.

 

Свертка показателей.

Способ свертки зависит от характера показателей и целей оценивания систем. Известны несколько видов свертки. Наиболее часто использую аддитивная и мультипликативная свертки компонентов векторного критерия.

Аддитивная свертка компонентов векторного критерия состоит в представлении обобщенного скалярного критерия в виде суммы взвешенных нормированных частных критериев:

 

          (3‑1)

 

Такие критерии образуют группу аддитивных критериев, их свертка основана на использовании принципа справедливой компенсации абсолютных значений нормированных частных критериев. Сутью этого принципа является утверждение: справедливым следует считать такой компромисс, при котором суммарный уровень абсолютного снижения значений одного или нескольких показателей не превышает суммарного уровня абсолютного увеличения значений других показателей. Главный недостаток аддитивных критериев состоит в том, что они не вытекают из объективной роли частных критериев определении качества системы и выступают поэтому как формальный математический прием, придающий задаче удобный вид. Кроме того, низкие оценки по одним критериям могут компенсироваться высокими оценками по другим критериям. Это значит, что уменьшение одного из критериев вплоть до нулевого значения может возмещаться возрастанием другого.

Мультипликативная свертка критерия состоит в представлении обобщенного скалярного критерия в виде произведения:

 

     (3‑2)

 

Мультипликативный критерий образуется путем перемножения частных критериев  возведенных в степени . Если все частные критерии имеют одинаковую важность, то  =1. При разной важности критериев ≠1.

В мультипликативных критериях компромисс достигается по отношению не к абсолютным, а к относительным изменениям частных критериев, а именно, суммарный уровень относительного снижения значений одного или нескольких критериев не превышает суммарного уровня относительного увеличения значений других критериев.

Достоинством мультипликативного критерия является то, что при его использовании не требуется нормировки частных критериев. К его недостаткам относится то, что он компенсирует недостаточную величину одного частного критерия избыточной величиной другого и имеет тенденцию сглаживать уровни частных критериев за счет неравнозначных первоначальных значений частных критериев.

Выбор между аддитивной и мультипликативной свертками частных критериев определяется степенью важности абсолютных или относительных изменений значений частных критериев соответственно.

 

3.3.Содержание работы.

В работе необходимо провести оценивание шести систем по четырем критериям качества. В качестве исходных данных задаются:

-   условие оптимальности  (max или min) каждого критерия;

-   вектор приоритетов критериев l=(l1,… l4 );

-   вектор значений критериев  ) для каждого оцениваемого образца.

 

Вариант исходных данных определяется порядковым номером студента в списке группы.

1) Откройте приложение  Microsoft Excel.

2) Подготовьте рабочую таблицу со структурой, показанной на Рис. 3‑3:

 

В ячейки подраздела Натуральные раздела Критерии заносятся исходные данные .

Ячейки подраздела Формула A раздела Критерии предназначены для занесения в них нормированных значений критериев, вычисленных по формуле:


 

Критерии

Парето

Оптимальность

Превосходство

Аддитивная

свертка

Мультипликативная

свертка

Натуральные

Формула
A

Формула
B

Формула A

Формула B

li=1

l≠1

k1

k2

k3

k4

k1

k2

k3

k4

k1

k2

k3

k4

К

К*

К

К*

К

К*

К

К*

 

Рис. 3‑3. Структура Excel-таблицы для проведения расчетов по оцениванию систем

 

 

Ячейки подраздела Формула A раздела Критерии предназначены для занесения в них нормированных значений критериев, вычисленных по формуле:

 

 

В ячейки столбца Парето заносятся:

В ячейки столбца Оптимальность заносятся:

В ячейки столбца Превосходство заносятся:

 

Ячейки подраздела Формула A раздела Аддитивная свертка предназначены для занесения в них скалярных значений критериев, вычисленных по формуле (3‑1) на основе значений критериев, нормированных на основе формулы A. В столбце K заполняются все ячейки, столбце K* заполняются ячейки для систем (строк), входящих в множество Парето.

Ячейки подраздела Формула B раздела Аддитивная свертка предназначены для занесения в них скалярных значений критериев, вычисленных по формуле (3‑1) на основе значений критериев, нормированных на основе формулы B. В столбце K заполняются все ячейки, столбце K* заполняются ячейки для систем (строк), входящих в множество Парето.

Для вычисления значения скалярного критерия используются значения приоритета , заданные в исходных данных , где  - значение приоритета, заданное в исходных данных.

Ячейки подраздела l=1 раздела Мультипликативная свертка предназначены для занесения в них скалярных значений критериев, вычисленных по формуле (3‑2) в предположении равных приоритетов критериев (li=1). В столбце K заполняются все ячейки, столбце K* заполняются ячейки для систем (строк), входящих в множество Парето.

Ячейки подраздела l≠1 раздела Мультипликативная свертка предназначены для занесения в них скалярных значений критериев, вычисленных по формуле (3‑2) в предположении равных приоритетов критериев. В столбце K заполняются все ячейки, столбце K* заполняются ячейки для систем (строк), входящих в множество Парето. Приоритеты критериев назначаются по правилу:

 

 

где

 - значение приоритета, заданное в исходных данных

 -минимальное значение, заданное в исходных данных

 

3) Проведите все необходимые расчеты (заполните все ячейки с вычисляемыми значениями необходимыми выражениями) и определите оптимальную систему для всех восьми случаев.

4) Проанализируйте полученные результаты.

 

3.4.Отчет о работе.

Отчет должен содержать таблицу с исходными данными и промежуточными расчетами и полученные результаты.

 

 

Рис. 3‑4. Пример отчета

 

Левая нижняя часть excel-листа содержит исходные и данные и ячейки для вспомогательных значений, используемых в выражениях для подсчета нужных значений.

В правой нижней части excel-листа приводятся полученные результаты – вычисленные значения скалярного критерия и номера наилучшей системы.

 

3.5.Контрольные вопросы.

1) Что называется частным показателем качества системы?

2) Что такое обобщенный показатель качества системы?

3) На какие основные классы распадаются критериев оценки сложных систем?

4) Какие элементы образуют множество Парето?

5) Как определяется аддитивный критерий свертки?

6) Из каких основных этапов состоит процедура свертки?

7) Как определяется мультипликативный критерий свертки?

8) В чем заключаются преимущества и недостатки аддитивного и мультипликативного критериев свертки?

 

3.6.Варианты.

 

1

k1

k2

k3

k4

1

3

2

4

2

2

6

4

1

1

3

5

2

5

1

4

4

1

5

3

5

3

7

5

4

6

2

1

7

3

li

0.25

0.20

0.20

0.35

Kопт

max

max

min

max

 

2

k1

k2

k3

k4

1

3

3

4

3

2

5

3

1

2

3

3

3

6

1

4

4

1

7

3

5

2

8

5

1

6

3

2

5

3

li

0.15

0.40

0.20

0.25

Kопт

max

max

min

max

 

3

k1

k2

k3

k4

1

3

2

4

3

2

8

3

1

2

3

3

3

6

1

4

4

1

7

3

5

2

4

2

1

6

3

2

5

3

li

0.30

0.30

0.15

0.25

Kопт

min

min

min

max

 

4

k1

k2

k3

k4

1

3

2

5

2

2

6

3

1

2

3

3

7

6

1

4

4

1

7

3

5

2

4

5

1

6

3

2

5

3

li

0.10

0.40

0.10

0.35

Kопт

min

max

min

max

 

5

k1

k2

k3

k4

1

3

2

4

2

2

7

4

1

3

3

5

2

6

1

4

6

1

5

3

5

2

4

5

4

6

2

1

8

3

li

0.35

0.20

0.10

0.35

Kопт

min

min

min

max

 

6

k1

k2

k3

k4

1

3

3

4

3

2

5

3

1

2

3

3

3

6

1

4

4

1

7

3

5

2

8

5

1

6

3

2

5

3

li

0.15

0.40

0.20

0.25

Kопт

max

max

min

max

 

7

k1

k2

k3

k4

1

3

2

4

3

2

8

3

1

2

3

3

3

6

1

4

4

1

7

2

5

2

4

2

1

6

3

2

5

3

li

0.20

0.40

0.15

0.25

Kопт

min

max

min

min

 

8

k1

k2

k3

k4

1

3

2

4

3

2

8

3

1

2

3

3

3

6

1

4

4

1

9

3

5

2

7

2

1

6

3

4

1

3

li

0.30

0.30

0.15

0.25

Kопт

min

min

min

max

 

9

k1

k2

k3

k4

1

3

5

3

3

2

8

4

2

3

3

5

2

6

1

4

6

1

5

3

5

2

4

5

2

6

2

1

8

3

li

0.20

0.40

0.15

0.25

Kопт

min

max

min

min

 

10

k1

k2

k3

k4

1

3

3

4

3

2

4

3

1

2

3

3

3

6

1

4

4

4

7

3

5

2

3

5

8

6

1

2

5

3

li

0.50

0.20

0.15

0.15

Kопт

min

max

max

min

 

11

k1

k2

k3

k4

1

3

2

4

3

2

5

3

1

2

3

3

4

6

1

4

4

1

7

2

5

2

6

2

1

6

3

2

5

3

li

0.20

0.40

0.15

0.25

Kопт

max

max

min

min

 

12

k1

k2

k3

k4

1

1

2

4

3

2

7

3

1

2

3

3

3

6

1

4

4

1

9

3

5

2

7

2

1

6

3

4

1

3

li

0.30

0.30

0.15

0.25

Kопт

min

min

max

max

 

13

k1

k2

k3

k4

1

3

2

5

2

2

5

3

1

2

3

3

7

6

1

4

4

2

7

3

5

2

4

5

1

6

3

2

5

3

li

0.10

0.40

0.15

0.35

Kопт

max

min

min

max

 

14

k1

k2

k3

k4

1

5

2

4

2

2

7

1

1

6

3

5

2

6

1

4

6

8

5

3

5

2

4

6

4

6

2

7

8

3

li

0.35

0.20

0.10

0.35

Kопт

min

min

min

max

 

15

k1

k2

k3

k4

1

3

2

4

3

2

7

3

1

2

3

3

3

6

1

4

4

2

7

3

5

3

4

2

1

6

4

2

5

3

li

0.30

0.30

0.15

0.25

Kопт

min

max

min

max

 

16

k1

k2

k3

k4

1

4

3

4

3

2

6

3

1

4

3

3

3

6

1

4

4

2

8

3

5

3

4

2

1

6

5

2

4

3

li

0.25

0.20

0.25

0.30

Kопт

max

min

min

min

 

17

k1

k2

k3

k4

1

3

3

4

3

2

2

3

1

4

3

1

3

6

3

4

3

4

7

4

5

8

3

5

2

6

3

2

5

1

li

0.50

0.20

0.15

0.15

Kопт

min

min

max

min

 

18

k1

k2

k3

k4

1

3

2

4

3

2

3

4

1

2

3

3

1

6

1

4

4

1

3

2

5

2

6

2

1

6

3

2

5

3

li

0.20

0.40

0.15

0.25

Kопт

max

max

min

min

 

19

k1

k2

k3

k4

1

3

2

4

3

2

6

3

1

2

3

3

3

6

1

4

4

1

8

3

5

2

7

2

1

6

3

4

1

3

li

0.35

0.30

0.15

0.20

Kопт

min

min

min

max

 

20

k1

k2

k3

k4

1

3

5

3

3

2

8

4

2

3

3

5

2

6

1

4

6

1

5

3

5

2

4

5

2

6

2

1

8

3

li

0.25

0.35

0.20

0.20

Kопт

min

max

min

min

 

21

k1

k2

k3

k4

1

1

2

4

3

2

7

3

1

2

3

3

3

6

1

4

4

1

9

3

5

2

7

2

1

6

3

4

5

3

li

0.25

0.25

0.15

0.35

Kопт

min

min

max

max

 

22

k1

k2

k3

k4

1

3

4

5

2

2

5

3

1

2

3

3

7

6

1

4

4

2

7

3

5

2

4

5

1

6

3

2

5

3

li

0.15

0.35

0.15

0.35

Kопт

min

max

min

max

 

23

k1

k2

k3

k4

1

3

2

4

3

2

8

3

1

2

3

3

3

6

4

4

4

5

7

3

5

3

4

2

1

6

4

2

5

3

li

0.10

0.35

0.20

0.35

Kопт

max

max

min

max

 

24

k1

k2

k3

k4

1

3

2

4

3

2

4

4

1

2

3

3

1

6

1

4

5

1

3

2

5

2

6

2

1

6

3

2

5

3

li

0.30

0.30

0.15

0.25

Kопт

max

max

min

min

 

4. Сетевое планирование и управление.

4.1.         Цель работы:

 

Изучение детерминированной и вероятностной сетевой модели планирования и управления.

 

4.2.Теоретические сведения.

4.2.1. Основные понятия.

Сетевое планирование и управление [5] – метод исследования и проектирования сложных систем. Метод позволяет провести анализ и оптимизацию процессов, состоящих из связанных подсистем или совокупности последовательных и взаимосвязанных работ и событий. Основой для анализа и расчетов процессов является математическая модель в виде ориентированного графа [

Рис. 4‑1], называемая сетевой моделью.

 

 

Рис. 4‑1 Пример простейшей сетевой модели

 

Основными элементами сетевой модели являются событие, работа и путь.

Работа - процесс, связанный с затратами времени и ресурсов, и приводящий к достижению определенных результатов. (Работами следует считать также процессы, не требующие расходов ресурса, но только времени).

Ресурсы - материалы, сырье, оборудование, контингент исполнителей, необходимые для производства работы, финансовые средства и прочее.

Фиктивная работа отображает логическую связь работ и не требует расхода времени и ресурсов (работа (1,3) на

Рис. 4‑1). Она только констатирует, что событие (3) не может произойти, пока не свершится событие (1).

В сетевых моделях работы отображаются направленными стрелками, фиктивная работа – пунктиром, рядом с ними изображаются длительности работ t(i,j).

Событие - факт завершения всех предшествующих работ и готовности к выполнению всех последующих.

Каждая работа в сети характеризуется:

-    начальным событием – (i);

-    конечным событием – (j);

 

Работы кодируются в терминах событий, т.е. каждая из них идентифицируется своими начальным и конечным событиями. Работы с одинаковыми i j не допускаются. В этом случае следует ввести фиктивные работы, которые обеспечивают необходимую развязку.

Исходное событие («самое начальное») сети (0) иногда обозначается (I); завершающее событие («самое конечное») – (С).

 

4.2.2. Нумерация событий.

Для любой работы сетевой модели:

-  номер начального события должен быть меньше номера конечного события (i < j) и

-  каждый путь должен проходить по возрастающей последовательности номеров событий.

 

Для нумерации событий используется алгоритм вычеркивания дуг, который также позволяет обнаруживать структурные ошибки:

-  отыскивается начальное событие (в него не входит ни одна работа), которому присваивается номер 0.

-  зачеркиваются работы, выходящие из него;

-  определяются события, не имеющие входящих работ (первый ранг),

-  выявленные события нумеруются в произвольном порядке (1, 2 или 2, 1);

-  зачеркиваются работы, выходящие из них, определяются события второго ранга;

-  по достижении конечного события процесс прекращается.

 

4.2.3. Критический путь.

Путь – последовательность работ в сети, в которой конечное событие любой работы совпадает с начальным событием следующей за ней работы.

Путь кодируется в событиях, через которые он проходит, например, путь (3,5,6), иногда он обозначается начальным и конечным событиями пути – L(3,6).

Наибольший интерес представляют собой  полные пути (в дальнейшем – просто путь), идущие от начального события до конечного события.

Если известны все длительности работ на сетевой модели, то можно определить продолжительность любого пути  T(L) как:

Например, для путей

Рис. 4‑1:

-   T(L(0,1,4,6))=28;

-   T(L(0,1,3,5,6))=30;

-   T(L(0,3,5,6))=27;

-   T(L(0,2,5,6))=23;

-   T(L(0,2,6))=21.

 

Путь, имеющий наибольшую продолжительность, называется критическим. Lкр, и длительность его обозначается Tкр.

В рассматриваемом примере Lкр =(0, 1, 3, 5, 6),  Tкр =30.

Работы, находящиеся на критическом пути, называются критическими. В рассматриваемом случае это работы (0,1), (1,3), (3,5), (5,6).

Критические работы выделяются на сетевой модели жирными или двойными стрелками.

Время выполнения проекта в целом не может быть меньше Tкр, поэтому первая задача при анализе сетевых моделей – выявление Lкр и критических работ и поиск возможностей по сокращению их длительности. Нахождение критического пути является основной задачей метода критического пути. В методах анализа сетевой модели используются временные характеристики событий и работ.

 

4.2.4. Временные параметры событий.

Ранний срок:

tp(i)=max(T(L(I,i))                            

Поздний срок:

tп(i) = Tкр - T (max L(i,C)) = min(Tкр -T (L(i,C)))       

Резерв события R(i), или резерв времени:

R(i)= tп (i) - t p(i)

 

4.2.5. Временные параметры работ.

Ранний срок начала tpн(i,j) (раннее начало):

tpн(i,j) = tp(i)

Ранний срок окончания (ранее окончание):

tpо(i,j) = tpн(i,j) + t(i,j) = tp(i) + t(i,j)

Поздний срок окончания t по(i,j)  (позднее окончание):

tпо(i,j) = tп(j)

Поздний срок начала tпн(i,j) (позднее начало):

tпн(i,j)= tп(j)- t (i,j)

Резерв работы (полный резерв):

Rп(i,j) = tп(j) - tр(i)- t(i,j)

 

4.2.6. Порядок расчета детерминированной сетевой модели.

Графический метод.

Метод основан на использовании графа модели, где вершины для удобства разделены на четыре сектора для записи значений:

i    - номер события,

tp(i)   – раннее время события

tп(i)   – позднее время события

R(i)   – резерв

 

Процесс расчета сетевой модели начинается с нумерации событий, затем осуществляется последовательный проход по цепочке событий справа налево с заполнением поля tp(i), затем – обратный проход с заполнением поля tп(i). После этого заполняется поле R(i).

При заполнении полей tp(i) и tп(i) вместо используются рекуррентные формулы:

tp(j) = max{ tp(i)+ t (ij), … tp(l)+ tp(lj)}

tп(j) = min{ tп(m) - tp(jm), … tп(k) - tp(jk)}

что позволяет свести процесс к просмотру окрестностей текущего события.

 

Табличный метод.

Табличный метод основан на использовании более детализированного по сравнению с информацией о событиях реестра работ, представленного в виде таблицы с временными характеристики работ, например:

 

Работы

Временные характеристики работ

i

j

t рн(i,j)

t(i,j)

t ро(i,j)

t пн(i,j)

t(i,j)

t по (i,j)

R п(i,j)

0

1

0

1

1

1

1

2

1

0

2

0

5

5

0

5

5

0

1

2

1

3

4

2

3

5

1

1

3

1

2

3

9

2

11

8

2

3

5

6

11

5

6

11

0

2

4

5

5

10

8

5

13

3

3

4

11

0

11

13

0

13

2

3

5

11

5

16

11

5

16

0

4

5

11

3

14

13

3

16

2

Порядок заполнения колонок

1

2

4

3

5

13

3

6

8

 

В нижней строке таблицы указан порядок выполнения расчетов, включающий:

- нумерацию событий (i,j);

- занесение в таблицу длительностей работ t(i,j) (колонки дублируются, чтобы облегчить последующее заполнение колонок tро(i,j) и tпн(i,j);

- сортировка строк в лексикографическом порядке (десятичные числа, образуемые парами (i,j) должны возрастать);

- проход слева направо и заполнение колонок tрн(i,j) и tро(i,j)   (tро(i,j) =  tрн(i,j) +  t (i,j) );

- проход справа налево и заполнение колонок tпо(i,j) и tпн(i,j)   (tпн(i,j) = tпо(i,j) - t (i,j) );

- заполнение колонки Rп (i,j).

 

4.2.7. Вероятностная сетевая модель.

В реальной действительности имеет место неопределенность как в структуре графа (те или иные события или работы могут присутствовать или же нет), так и во временных параметрах - времена выполнения работ, моменты наступления событий, резервы и пр. Одним из распространенных методов расчета является метод PERT , использующий ряд упрощающих предположений по сравнению с общей постановкой задачи расчета вероятностных сетей:

1) Предполагается, что времена работ t(i,j) подчиняются β-распределению, в котором параметры αij и γij  одинаковы для всех работ, причем

 

αij =α =1

γij =γ=2

 

Тогда функция распределения длительности работы (i,j) принимает вид:

 

 

Где

 

 

Для таких распределений в качестве приближенных значений для моментов могут быть приняты следующие оценки

Математическое ожидание:

 

 

Дисперсия:

 

 

2) Предполагается статистическая независимость длительностей работ.

3) Предполагается, что длительность критического пути настолько превосходит (в среднем) длительности прочих полных путей, что практически невозможен его случайный «перескок» на другие пути.

 

4.2.8. Порядок расчета вероятностной модели методом PERT.

После того, как осуществлена нумерация вершин и собраны данные по tmax и tmin проводятся следующие расчеты.

1) Вершины графа нумеруются;

2) Для всех работ собираются данные по tmax и tmin;

3) Определяются моменты распределений длительностей работ tож(i,j), ;

4) На основании совокупности значений t(i,j) = tож(i,j) проводится обычный расчет характеристик, как для детерминированной сетевой модели;

5) Определяется критический путь Lкр и его среднее значение

 

 

6) Определяется дисперсия  длительностей Lкр как сумма дисперсий длительностей критических работ (предположение о независимости работ)

 

 

7) Поскольку длительности t(i,j) – независимые случайные величины, их сумма Tкр может трактоваться как случайная величина, распределенная по нормальному закону  с матожиданием  и  дисперсией , для которого функция плотности вероятности имеет вид:

 

 

8) Поскольку из свойств нормального распределения следует (правило «трех сигма»), что с вероятностью 0,9974 значение Ткр будет находиться в интервале

 

,

 

можно утверждать, что

 

,

 

9) Пусть определен некоторый плановый срок выполнения всего проекта – Тпл.

Вероятность P (Tкр ≤ T) выполнения работы в срок определяется следующим образом:

 

 

Для того, чтобы получить конкретные значения для этой функции, необходимо перейти от  к стандартному табулированному распределению .  С этой целью осуществляется замена переменной:

 

 

что приводит к изменению подинтегральной функции и пределов интегрирования:

y=0

Тогда

и

 

где Ф(х) называется функцией Лапласа и табулирована. Значение ее можно также получить с использованием библиотечных функций, которые присутствуют во многих компиляторах и программных пакетах. В частности, в табличном процессоре Microsoft Excel она представлена функцией нормстрасп().

 

4.3.Содержание работы.

Вариант работы определяется порядковым номером студента в списке группы.

Работа выполняется с помощью табличного редактора Microsoft Excel.

1. Согласно указаниям столбца Топология таблицы вариантов работ постройте сетевой граф для своего варианта работы.

В записи, определяющей вид графа, используется следующая нотация.

A-B    Граф образуется из частичных графов A и B таким образом, что сливаются правая вершина частичного графа с номером A и левая  вершина частичного графа с номером B, а все дуги остаются в образованном графе.

Например, обозначение 2-3 в результате дает граф:

 

 

(A:B) Граф образуется из частичных графов A и B таким образом, что сливаются правая вершина частичного графа с номером A и правая  вершина частичного графа с номером B, левая вершина частичного графа с номером A и левая вершина частичного графа с номером B,  а все дуги остаются в образованном графе.

Например, обозначение (2:3) подразумевает граф:

 

 

Поскольку такой граф недопустим (две работы начинаются и заканчиваются в одной и той же паре вершин), то такой граф требуется преобразовать, например, так:

 

 

Для исключения неоднозначности здесь добавлена фиктивная работа.

Желательно готовить электронный вариант изображения графа в каком-либо графическом редакторе (например, MS Visio).

2. Пронумеруйте вершины графа, используя алгоритм вычеркивания дуг.

3. В приложении Microsoft Excel подготовьте таблицу следующего вида

 

Код

i

j

Tмин(ij)

Tмакс(ij)

Tож(ij)

σ2 (ij)

a

 

 

 

 

 

 

b

 

 

 

 

 

 

…

..

..

…

…

…..

…

 

В ячейках каждой строки таблицы размещаются:

Код - код работы

i - номер начальной вершины работы, обозначенной кодом

j - номер конечной вершины работы, обозначенной кодом

Tмин(ij) – минимальная продолжительность работы, значение берется из таблицы для минимальных продолжительностей работ из ячейки, стоящей на пересечении строки с кодом работы и столбца с номером, указанном в ячейке на пересечении столбца Tмин  и строки с номером варианта таблицы вариантов.

Tмакс(ij) – максимальная продолжительность работы, значение берется из таблицы для максимальных продолжительностей работ из ячейки, стоящей на пересечении строки с кодом работы и столбца с номером, указанном в ячейке на пересечении столбца Tмакс  и строки с номером варианта таблицы вариантов

Tож(ij)  – математическое ожидание продолжительности работы, значение рассчитывается на основании выражения раздела 4.2.7

σ2 (ij)  – дисперсия продолжительности работы, значение рассчитывается на основании выражения раздела 4.2.7

Заполните таблицу числовыми значениями для своего варианта.

4. Подготовьте таблицу для расчета детерминированной модели:

 

i

j

Tрн(ij)

Tож(ij)

Tро(ij)

Tпн(ij)

Tож(ij)

Tпо(ij)

Rп(ij)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Для каждой работы внесите в таблицу рассчитанные в предыдущем пункте значения  Tож(ij)  и выражения для нахождения Tро(ij), Tпн(ij), Rп(ij).

5. С помощью таблицы проведите расчет детерминированной модели.

6. С использованием полученных результатов проведите расчет параметров вероятностной модели:

Ткр.ож            =   _______

σ2кр                 =   _______

Ткр.мин           =   _______

Ткр.макс         =   _______

Тпл1                =   _______

P(Тпл1> Т кр )     =      _______

Тпл2                =   _______

P(Тпл2 > Т кр ) = _______

 

Оценивание P(Т пл>Т кр) проводится для двух значений плановых сроков Тпл1 и Тпл2. В качестве Тпл1 и Тпл2 берутся значения:

1)  Тпл1 = Entier (Ткр.ож / 5) * 5.

2)  Тпл2 = Entier (Ткр.ож / 5) *5+5

 

Например, если Ткр.ож =98, то следует взять 

1)  Тпл1=95;  

2)  Тпл2 =100

 

4.4.         Отчет по работе.

Отчет по работе должен включать исходные данные и результаты.

1. Таблицу с исходными  данными варианта.

 

№

Топология

Строка
таблицы
Tмин

Строка
таблицы
Tмакс

 

 

 

 

 

Таблица содержит одну строку – копию из таблицы раздела 4.6 с данными варианта работы.

2. Таблицу с временными параметрами работ (см. раздел 4.3)

3. Таблицу с временными параметрами детерминированной модели (см. раздел 4.3)

4. Результаты расчета временных параметров вероятностной модели (см. раздел 4.3)

 

4.5.Контрольные вопросы.

1)      Что называется сетевой моделью?

2)      Какие задачи решаются с помощью сетевой модели?

3)      Как определяется событие?

4)      Что называется работой?

5)      Что такое фиктивное работа и для чего она используется?

6)      В чем заключается суть алгоритма расстановки пометок?

7)      Что такое путь?

8)      Какой путь называется критическим, каков его физический смысл?

9)      Какие временные параметры событий используются для описания сетевой модели?

10) Какие временные параметры работ используются для описания сетевой модели?

11) В чем могут состоять отличия вероятностной сетевой модели от детерминированной?

12) На каких предположениях основан метод расчета вероятностных моделей с помощью средних?

13) Из каких основных шагов состоит метод расчета вероятностных моделей с помощью средних?

 

4.6.         Варианты.

 

Варианты задания

 

№

Топология

Строка
таблицы
Tмин

Строка
таблицы
Tмакс

1

(1 : 2) – 3 – 4 – 5

1

1

2

1 – (2 : 5) – 3 – 4

2

1

3

3 – 4 – (1 : 5) – 2

3

1

4

(2 : 3) – (1 : 4) – 5

4

1

5

5 – (1 : 4) – 3 – 2

5

1

6

4 – (1 : 2) – 5 – 3

6

1

7

(1 : 4) – 5 – 3 – 2

7

1

8

4 – (5 : 1) – 2 – 3

8

1

9

2 –  3 – 5 – (4 : 1)

9

1

10

4 –3 – (2 : 5) – 1

10

1

11

3 – 4 – (2 : 1) – 5

11

1

12

(5 : 3) – (2 : 4) – 1

12

1

13

3 – (4 : 5) – 1 – 2

13

1

14

1 – 2 – 3 – (5 : 4)

14

1

15

5 – 4 – 3 – (1 : 2)

15

1

16

3 – 4 – 5 – (1 : 2)

1

2

17

3 – (2 : 5) – 4 – 1

2

2

18

(4 : 5) – 1 – 3– 2

3

2

19

2 – 1 – (4 : 5) – 3

4

2

20

(2 : 5) – 1 – 4 – 3

5

2

21

2 – 5 – (1 : 4) – 3

6

2

22

(1 : 4) – 2 – 3 – 5

7

2

23

3 – 1 – (2 : 5) – 4

8

2

24

(5 : 1) – 4 – 2 – 3

9

2

25

2 – 3 – (1 : 5) – 4

10

2

26

4 – 3 – 2 – (1 : 5)

11

2

27

(2 : 4) – 5 – 3 – 1

12

2

28

2 – 5 – 3 – (1 : 4)

13

2

29

3 – (1 : 5) – 4 – 2

14

2

30

5 – 3 – (2 : 4) – 1

15

2

 

Частичные сетевые графики

 

1

 

 

 

 

2

 

 

 

3

 

 

 

 

 

4

 

 

5

 

 

 

Минимальные оценки длительности работ Tмин

 

 

а

б

в

г

д

е

ж

з

и

к

л

м

н

о

п

р

1

2

3

7

2

6

4

7

2

2

4

2

5

7

4

5

8

2

3

2

6

4

2

3

6

2

4

2

9

2

2

4

2

4

3

4

2

3

9

2

4

2

9

2

6

7

2

3

7

5

9

4

3

4

4

2

6

7

5

9

3

4

5

7

8

3

5

2

5

6

7

5

2

6

4

2

1

2

2

4

3

5

9

2

4

6

1

2

5

2

5

7

5

9

5

6

3

1

1

4

4

3

7

9

9

9

6

3

7

6

7

6

6

6

2

4

7

7

8

8

7

4

2

7

4

3

3

7

3

2

5

4

4

5

6

4

9

5

3

2

3

2

9

6

2

8

8

2

5

2

8

6

5

10

9

5

5

8

9

8

7

9

4

8

6

3

5

8

4

6

11

9

2

6

6

3

7

5

7

8

5

7

2

2

2

4

7

12

3

5

2

1

5

7

6

7

8

7

5

7

9

9

4

7

13

4

6

3

2

9

2

9

4

5

9

9

7

4

2

2

5

14

5

2

5

5

9

5

8

8

7

9

3

4

9

3

5

7

15

4

5

5

7

7

6

9

9

7

4

7

8

2

6

4

9

 

Максимальные оценки длительности работ Tмакс

 

 

а

б

в

г

д

е

ж

з

и

к

л

м

н

о

п

р

1

10

13

14

18

10

13

13

15

19

12

16

11

14

13

12

10

2

17

19

10

12

13

18

15

16

16

13

15

14

17

17

12

14

 

5. Оценивание в условиях риска и неопределенности

Цель работы: практическое изучение методов оценивания альтернатив в различных условиях функционирования сложных систем.

 

5.1.         Теоретические сведения

5.1.1. Задача количественного оценивания

Количественное оценивание систем необходимо во многих практических случаях, связанных с необходимостью принятия решений или осуществления управления в сложных системах.

Существенным для выбора того или иного критерия являются условия, в которых функционирует оцениваемая система. Различают три группы условий [1]:

-  условия определенности,

-  условия риска,

-  условия неопределенности.

Рассмотрим второй и третий случай из указанных выше.

 

5.1.2. Оценка сложных систем в условиях риска на основе функции полезности.

Операции, выполняемые в условиях риска, называются вероятностными. Однозначность соответствия между системами и исходами в вероятностных операциях нарушается. Это означает, что каждой системе (альтернативе) ai ставится в соответствие не один, а множество исходов {yk} с известными условными вероятностями появления . Следовательно, оценивать системы в операциях данного типа так, как в детерминированных операциях, нельзя.

Эффективность систем в вероятностных операциях находится через математическое ожидание функции полезности на множестве исходов K(a)=Ma[F(y)].

При исходах yk (k=1,…m)  с дискретными значениями показателей, каждый из которых появляется с условной вероятностью  и имеет полезность F(yk) выражение для математического ожидания функции полезности записывается в виде:

 

 

Из этого выражения может быть получена оценка эффективности детерминированных систем как частный случай, если принять, что исход детерминированной системы наступает с вероятностью равной 1, а вероятности всех остальных исходов равны 0. Условия оценки систем в случае, когда показатели исхода вероятностной операции являются дискретными величинами, удобно задавать в табличном виде:

 

ai

yk

p (yk / ai) 

F(yk)

K(ai )

a1

y1

y2

…

ym

p (y1 / a1)

p (y2 / a1)

…

p (ym / a1)

F(y1)

F(y2)

…

F(ym)

 

a2

y1

y2

…

ym

p (y1 / a2)

p (y2 / a2)

…

p (ym / a2)

F(y1)

F(y2)

…

F(ym)

 

…

…

 

 

 

an

y1

y2

…

ym

p (y1 / an)

p (y2 / an)

…

p (ym / an)

F(y1)

F(y2)

…

F(ym)

 

 

Таким образом, для оценки эффективности систем в вероятностной операции необходимо:

1) Определить исходы операции на каждой системе

2) Построить функцию полезности на множестве исходов операции

3) Рассчитать математическое ожидание функции полезности на множестве исходов операции для каждой системы.

 

Критерий оптимальности для вероятностных операций имеет вид:

 

 

В соответствии с этим критерием оптимальной системой в условиях риска считается система с максимальным значением математического ожидания функции полезности на множестве исходов операции.

Оценка систем в условиях вероятностной операции – это “оценка в среднем”, поэтому ей присущи все недостатки такого подхода, главный из которых заключается в том, что не исключен случай выбора неоптимальной системы для конкретной реализации операции. Однако если операция будет многократно повторяться, то система оптимальная в среднем приведет к наибольшему успеху.

 

5.1.3. Оценка сложных систем в условиях неопределенности.

Организационно-технические системы имеют специфические черты, не позволяющие свести их ни к детерминированным, ни к вероятностным, что не позволяет использовать для их оценки детерминированные или вероятностные критерии. Условия оценки эффективности систем для неопределенных операций можно представить в виде таблицы

 

ai

nj

K(ai)

n1

n2

…

nk

a1

k11

k12

…

k1k

 

a2

k21

k22

…

k2k

 

…

…

…

…

…

…

an

kn1

Kn2

…

knk

 

 

Здесь:

ai   - вектор управляемых параметров, определяющий свойства системы (i=1,…n)

nj   - вектор неуправляемых параметров, определяющий состояние обстановки (i=1,…k)

kij   - значение эффективности системы ai для состояния обстановки nj

K(ai) -коэффициент эффективности системы (альтернативы) ai 

 

Каждая строка таблицы содержит значения эффективности одной системы для всех состояний обстановки nj, а каждый столбец - значения эффективности для всех систем ai для одного состояния обстановки.

В зависимости от характера предпочтений ЛПР в условиях неопределенных могут использоваться следующие критерии.

 

5.1.3.1.                 Критерий среднего выигрыша.

Предполагает задание вероятностей состояния обстановки pj. Эффективность систем оценивается как среднее ожидаемое значение (математическое ожидание) оценок эффективности по всем состояниям обстановки:

 

 

Оптимальной системе будет соответствовать эффективность

 

 

5.1.3.2.                 Критерий Лапласа.

В основе критерия лежит предположение: поскольку о состояниях обстановки ничего не известно, то их можно считать равновероятными. Поэтому:

 

 

 

5.1.3.3.                 Критерий осторожного наблюдателя (критерий Вальда).

Это максиминный критерий, гарантирующий максимальный выигрыш при наихудших условиях. Критерий основывается на том, что если состояние обстановки неизвестно, нужно поступить самым осторожным образом, ориентируясь на минимальное значение эффективности каждой системы.

В каждой строке матрицы эффективности находится минимальная из оценок систем по различным состояниям обстановки

 

 

Оптимальной считается система для строки с максимальным  значением эффективности:

 

 

5.1.3.4.                 Критерий максимакса.

Этим критерием предписывается оценивать системы по максимальному значению эффективности и выбирать в качестве оптимального решения систему, обладающую эффективностью наибольшей из максимумов:

 

 

5.1.3.5.                 Критерий пессимизма-оптимизма (критерий Гурвица).

Это критерий обобщенного максимина. Согласно данному критерию при оценке и выборе систем неразумно проявлять как осторожность, так и азарт, а следует, учитывая самое высокое и самое низкое значения эффективности, занимать промежуточное позицию (взвешиваются наилучшие и наихудшие условия). Для этого вводится коэффициент оптимизма α (0 <= α <=1), характеризующий отношение к риску лица, принимающего решения. Эффективность системы находится как взвешенная с помощью  коэффициента α сумма максимальной и минимальной оценок:

 

 

Условие оптимальности записывается в виде:

 

 

5.1.3.6.                 Критерий минимального риска (критерий Сэвиджа).

Критерий минимизирует потери эффективности при наихудших условиях. Для оценки систем на основе данного критерия матрица эффективности должна быть преобразована в матрицу потерь (риска). Каждый элемент матрицы потерь определяется как разность между максимальным и текущим значениями оценок эффективности в столбце

 

 

После преобразования матрицы используется критерий минимакса:

 

 

Критерии Сэвиджа как и критерий Вальда относится к числу осторожных критериев.

Необходимо отметить, что выбор какого-то критерия приводит к принятию решения по оценке систем, которое может быть совершенно отлично от решений, диктуемых другими критериями.

 

5.2.Содержание работы.

Вариант работы определяется порядковым номером в списке группы.

Работа выполняется в среде табличного редактора Microsoft Excel.

 

5.2.1. Оценивание в условиях риска.

1) Подготовьте в табличном редакторе Microsoft Excel таблицу со структурой, соответствующей структуре таблицы из раздела 5.1.2 (колонка для yk не используется).

2) Заполните столбцы для  p (yk / ai) и F(yk) данными своего варианта.

3) Впишите в первую строку столбца для K(ai ) выражение для вычисления математического ожидания применения альтернативы.

4) Определите альтернативу ai, которую следует считать наилучшей по критерию максимума математического ожидания.

 

5.2.2. Оценивание в условиях неопределенности.

1) Подготовьте в табличном редакторе Microsoft Excel таблицу со структурой, соответствующей структуре таблицы из раздела 5.1.3.

2) Заполните ячейки таблицы данными своего варианта.

3) Добавьте столбец для вычисления средневзвешенного значения по каждой операции (альтернативе) и впишите в его ячейки выражение из раздела 5.1.3.1.

4) Определите операцию ai, которую следует считать наилучшим вариантом в смысле максимума математического ожидания.

5) Повторите шаги 1-4 для каждого из критериев, описанных в разделе 5.1.3 (при оценивании по критерию Сэвиджа нужно будет дополнительно построить таблицу потерь).

Оценивание по критерию Гурвица должно быть выполнено дважды – один раз со значением a=a1, указанным первым в варианте задания, второй раз - со значением  a=a2, указанным в варианте задания вторым.

 

5.3.         Отчет по работе.

Отчет по работе должен включать исходные данные и результаты.

1) Результаты для заданий 1.3.1, 1.3.2 должны быть размещены на отдельных листах.

2) Таблицы по каждому критерию должны располагаться по левой стороне листа одна под одной и предваряться заголовком с названием критерия.

3) Результат (выбор) должен указывать на лучшую операцию по данному критерию и приводится непосредственно под заполненной таблицей.

4) Точность вычислений– два десятичных знака.

 

5.4.Контрольные вопросы.

1)      С какой целью необходимо проводить оценивание альтернатив?

2)      Что такое множество Парето и как оно используется в оценивании альтернатив?

3)      Какими условиями функционирования систем определяется выбор подхода  к оцениванию?

4)      Что может приниматься в качестве критерия выбора наилучшей альтернативы в условиях риска?

5)      Какие существуют методы выбора наилучшей альтернативы в условиях неопределенности?

6)      В чем состоит особенность критерия среднего выигрыша по отношению к другим критериям?

7)      Какие подходы могут применяться для оценивания альтернатив?

8)      Что такое “показатель”,  какие типы показателей существуют?

9)      Что такое обобщенный показатель, как можно осуществить переход к обобщенному показателю?

10) Зачем требуется нормирование показателей, какие правила для этого могут применяться?

 

5.5.Варианты.

5.5.1.              Оценивание в условиях риска.

Для каждого варианта приводятся:

-  значения вероятностей  появления исхода  для каждой альтернативы  (таблица),

-  значения показателей исходов  для каждой альтернативы (под таблицами).

 

1

p (yk / ai)

a1

0.30

0.40

0.30

a2

0.20

0.65

0.15

a3

0.25

0.60

0.15

F(y1)= 0.70

F(y2)= 0.50

F(y3)= 0.60

 

2

p (yk / ai) 

a1

0.20

0.50

0.30

a2

0.40

0.50

0.10

a3

0.15

0.30

0.55

F(y1)= 0.90

F(y2)= 0.60

F(y3) = 1.0

 

3

p (yk / ai) 

a1

0.20

0.50

0.30

a2

0.40

0.50

0.10

a3

0.15

0.30

0.55

F(y1)= 0.7

F(y2)= 0.5

F(y3)= 0.6

 

4

p (yk / ai)

a1

0.30

0.40

0.30

a2

0.20

0.65

0.15

a3

0.25

0.60

0.15

F(y1)= 0.9

F(y2)= 0.6

F(y3)= 1.0

 

5

p (yk / ai) 

a1

0.30

0.20

0.50

a2

0.55

0.35

0.10

a3

0.25

0.60

0.15

F(y1)= 0.7

F(y2)= 0.5

F(y3)= 0.6

 

6

p (yk / ai) 

a1

0.30

0.40

0.30

a2

0.20

0.65

0.15

a3

0.25

0.60

0.15

F(y1)= 1.2

F(y2)= 0.6

F(y3)= 1.0

 

7

p (yk / ai) 

a1

0.30

0.40

0.30

a2

0.20

0.65

0.15

a3

0.45

0.45

0.10

F(y1)= 1.2

F(y2)= 0.8

F(y3)= 1.0

 

8

p (yk / ai) 

a1

0.25

0.45

0.30

a2

0.50

0.35

0.15

a2

0.25

0.60

0.15

F(y1)= 3.2

F(y2)= 2.4

F(y3)=3.5

 

9

p (yk / ai) 

a1

0.55

0.30

0.15

a2

0.25

0.55

0.20

a3

0.25

0.60

0.15

F(y1)= 0.9

F(y2)= 0.6

F(y3)=1.0

 

10

p (yk / ai) 

a1

0.30

0.20

0.50

a2

0.55

0.35

0.10

a3

0.25

0.60

0.15

F(y1)= 0.7

F(y2)= 0.5

F(y3)= 0.6

 

11

p (yk / ai) 

a1

0.30

0.40

0.30

2

0.25

0.45

0.30

a3

0.55

0.30

0.15

F(y1)= 1.2

F(y2)= 0.6

F(y3)=1.0

 

12

p (yk / ai) 

a1

0.20

0.50

0.30

a2

0.40

0.50

0.10

a3

0.15

0.30

0.55

F(y1)= 1.6

F(y2)= 1.9

F(y3)=2.0

 

13

p (yk / ai) 

a1

0.30

0.40

0.30

a2

0.20

0.65

0.15

a3

0.25

0.60

0.15

F(y1)= 4.9

F(y2)= 5.6

F(y3)=4. 0

 

14

p (yk / ai) 

a1

0.50

0.25

0.25

a2

0.40

0.45

0.15

a3

0.45

0.30

0.25

F(y1)= 1.2

F(y2)= 0.8

F(y3)=1.0

 

15

p (yk / ai) 

a1

0.25

0.45

0.30

a2

0.50

0.35

0.15

a3

0.25

0.60

0.15

F(y1)= 0.8

F(y2)= 0.6

F(y3)=1.0

 

16

p (yk / ai) 

a1

0.55

0.30

0.15

a2

0.25

0.55

0.20

a3

0.25

0.60

0.15

F(y1)= 0.9

F(y2)= 1.0

F(y3)=1.3

 

17

p (yk / ai) 

a1

0.30

0.40

0.30

a2

0.20

0.65

0.15

a3

0.45

0.45

0.10

F(y1)= 3.2

F(y2)= 2.8

F(y3)=2.9

 

18

p (yk / ai) 

a1

0.25

0.45

0.30

a2

0.50

0.35

0.15

a3

0.25

0.60

0.15

F(y1)= 5.2

F(y2)= 3.4

F(y3)=4.5

 

19

p (yk / ai) 

a1

0.30

0.40

0.30

a2

0.20

0.65

0.15

a3

0.15

0.70

0.15

F(y1)= 1.9

F(y2)= 3.6

F(y3)=4.0

 

20

p (yk / ai) 

a1

0.10

0.50

0.40

a2

0.50

0.35

0.15

a2

0.25

0.60

0.15

F(y1)= 0.9

F(y2)= 0.6

F(y3)=1.0

 

21

p (yk / ai) 

a1

0.20

0.50

0.30

a2

0.20

0.65

0.15

a3

0.25

0.60

0.15

F(y1)= 2.8

F(y2)= 3.6

F(y3)=4.0

 

22

p (yk / ai) 

a1

0.30

0.20

0.50

a2

0.55

0.35

0.10

a3

0.25

0.60

0.15

F(y1)= 1.7

F(y2)= 2.5

F(y3)=0.6

 

23

p (yk / ai) 

a1

0.25

0.45

0.30

a2

0.50

0.35

0.15

a3

0.25

0.60

0.15

F(y1)= 7.6

F(y2)= 6.6

F(y3)=8.0

 

24

p (yk / ai) 

a1

0.55

0.30

0.15

a2

0.25

0.55

0.20

a3

0.25

0.60

0.15

F(y1)= 1.7

F(y2)= 2.1

F(y3)=3.7

 

25

p (yk / ai)  

a1

 

 

0.50

0.35

0.15

a2

0.25

0.40

0.35

a3

0.10

0.50

0.40

F(y1)= 1.7

F(y2)= 2.2

F(y3)=0.6

 

5.5.2. Оценивание в условиях неопределенности.

Для каждого варианта приводятся:

-  матрица значений Kij эффективности применения альтернативы ai для внешнего воздействия Nj  (первые пять строк таблицы);

-  вероятности pj появления каждого из воздействий Nj (последняя строка таблицы);

-  коэффициенты оптимизма a1 и a2 (записаны под таблицей) для двух вариантов оценивания по  критерию Гурвица).

 

1

N1

N2

N3

N4

N5

N6

a1

13,1

9,8

23,3

17,7

19,9

16,4

a2

15,7

10,1

16,8

13,3

15,5

16,9

a3

10,4

9,7

23,6

17,0

21,3

15,0

a4

17,6

7,8

19,6

17,7

19,9

18,3

a5

19,2

8,4

21,4

15,8

16,7

20,0

Pj

0,10

0,11

0,32

0,11

0,24

0,12

 

a1=0,1    a2=0,9

 

2

N1

N2

N3

N4

N5

N6

a1

9,7

22,3

17,7

18,8

14,3

13,1

a2

10,2

16,8

13,3

14,6

16,9

15,7

a3

9,7

22,2

17,0

22,3

11,9

10,4

a4

7,8

21,6

17,7

19,8

17,3

17,6

a5

7,5

22,4

14,8

17,6

21,0

19,2

Pj

0,20

0,09

0,12

0,25

0,11

0,23

 

a1=0,1    a2=0,9

 

3

N1

N2

N3

N4

N5

N6

a1

12,3

9,7

17,7

18,8

14,3

13,1

a2

14,8

10,2

13,3

14,6

16,9

15,7

a3

13,4

9,7

17,0

19,4

11,9

10,4

a4

15,6

7,8

18,7

19,4

17,3

17,6

a5

16,4

7,5

15,8

18,6

19,0

19,2

Pj

0,11

0,15

0,20

0,21

0,10

0,23

 

a1=0,4    a2=0,6

 

4

N1

N2

N3

N4

N5

N6

a1

10,4

15,7

10,3

13,1

13,3

14,4

a2

17,6

10,4

17,6

15,7

15,7

13,3

a3

17,3

17,6

19,2

14,7

15,7

16,9

a4

15,7

18,9

17,3

19,3

10,4

11,8

a5

12,0

15,7

17,8

18,9

17,6

17,0

Pj

0,12

0,19

0,11

0,23

0,22

0,13

 

a1=0,4    a2=0,6

 

5

N1

N2

N3

N4

N5

N6

a1

9,4

15,7

14,4

15,1

18,4

17,5

a2

11,6

12,4

17,6

15,7

17,3

15,3

a3

13,2

17,6

18,2

14,6

17,0

15,8

a4

8,7

19,9

17,3

18,3

18,0

14,8

a5

11,9

15,7

17,8

17,9

19,3

17,6

Pj

0,12

0,26

0,11

0,23

0,03

0,25

 

a1=0,4    a2=0,6

 

6

N1

N2

N3

N4

N5

N6

a1

13,4

15,5

14,6

15,5

18,4

17,3

a2

12,6

12,7

17,6

15,6

17,1

15,7

a3

13,2

17,6

18,3

14,5

16,9

14,9

a4

10,7

19,8

17,9

18,6

15,9

13,3

a5

15,0

13,3

17,8

17,7

19,6

17,6

Pj

0,12

0,19

0,31

0,23

0,03

0,12

 

a1=0,3    a2=0,8

 

7

N1

N2

N3

N4

N5

N6

a1

13,2

17,4

18,3

14,5

16,9

14,9

a2

10,7

19,7

17,9

18,6

15,9

13,3

a3

15,0

13,3

17,8

17,7

19,1

17,6

a4

13,4

15,5

14,6

15,5

18,4

17,3

a5

12,6

12,7

17,6

15,6

17,1

15,7

Pj

0,11

0,20

0,29

0,24

0,04

0,12

 

a1=0,9    a2=0,4

 

8

N1

N2

N3

N4

N5

N6

a1

18,3

17,4

13,2

14,1

14,9

16,9

a2

17,9

14,7

10,7

18,6

13,3

15,9

a3

17,8

13,0

15,0

17,7

17,1

17,6

a4

16,6

15,5

13,4

14,1

17,3

18,4

a5

17,6

12,7

12,6

15,6

15,7

17,1

Pj

0,20

0,18

0,11

0,05

0,12

0,34

 

a1=0,9    a2=0,5

 

9

N1

N2

N3

N4

N5

N6

a1

14,2

15,5

13,4

16,6

17,3

18,4

a2

18,7

12,7

12,6

17,6

15,7

17,1

a3

17,8

13,0

15,0

17,8

17,1

17,6

a4

14,1

12,7

12,6

17,6

15,7

17,1

a5

15,6

15,5

13,4

16,6

17,3

18,4

Pj

0,08

0,17

0,12

0,20

0,12

0,31

 

a1=0,8    a2=0,2

 

10

N1

N2

N3

N4

N5

N6

a1

15,6

15,6

13,4

16,6

17,3

18,4

a2

17,1

15,7

12,7

17,6

15,7

18,7

a3

17,6

17,1

13,0

17,8

17,1

17,8

a4

17,1

15,7

12,7

17,6

15,7

14,1

a5

14,2

15,5

13,4

16,6

17,3

18,4

Pj

0,31

0,12

0,17

0,20

0,12

0,08

 

a1=0,8    a2=0,4

 

11

N1

N2

N3

N4

N5

N6

a1

15,7

12,7

17,6

15,7

18,7

18,4

a2

17,1

13,0

16,2

16,1

17,8

18,7

a3

15,7

12,7

17,6

15,7

14,1

18,8

a4

15,5

13,4

16,6

17,3

18,4

14,1

a5

14,2

15,5

13,4

16,6

17,3

18,4

Pj

0,21

0,18

0,25

0,16

0,12

0,08

 

a1=0,8    a2=0,1

 

12

N1

N2

N3

N4

N5

N6

a1

15,8

12,3

15,7

17,6

18,7

18,4

a2

17,2

12,3

16,1

16,1

17,8

18,7

a3

15,8

12,6

15,7

17,6

14,1

18,8

a4

15,1

12,4

17,3

16,6

18,4

14,1

a5

14,5

15,5

16,6

13,4

17,3

18,4

Pj

0,26

0,25

0,12

0,16

0,08

0,13

 

a1=0,7    a2=0,3

 

13

N1

N2

N3

N4

N5

N6

a1

23,3

17,7

19,9

16,4

13,1

9,8

a2

16,8

13,3

15,5

16,9

15,7

10,1

a3

23,6

17,0

21,3

15,0

10,4

9,7

a4

19,6

17,7

19,9

18,3

17,6

7,8

a5

21,4

15,8

17,7

20,0

19,2

8,4

Pj

0,32

0,11

0,24

0,12

0,10

0,11

 

a1=0,2    a2=0,9

 

14

N1

N2

N3

N4

N5

N6

a1

14,3

13,1

17,7

18,8

9,7

22,3

a2

16,9

15,7

13,3

14,6

10,2

16,8

a3

14,9

10,4

17,0

22,3

9,7

22,2

a4

17,3

17,6

17,7

19,8

7,8

21,6

a5

21,0

19,2

14,8

17,6

7,5

22,4

Pj

0,11

0,23

0,12

0,25

0,20

0,09

 

a1=0,1    a2=0,9

 

15

N1

N2

N3

N4

N5

N6

a1

13,3

14,6

16,9

15,7

14,8

10,2

a2

17,0

19,4

11,9

10,4

13,4

9,7

a3

18,7

19,4

17,3

17,6

15,6

7,8

a4

15,8

18,6

19,0

19,2

16,4

7,5

a5

17,7

18,8

14,3

13,1

12,3

9,7

Pj

0,20

0,21

0,10

0,23

0,11

0,15

 

a1=0,4   a2=0,6

 

16

N1

N2

N3

N4

N5

N6

a1

14,4

17,6

17,6

15,7

15,7

13,3

a2

17,6

17,2

17,3

14,7

15,7

16,9

a3

15,7

10,3

10,4

13,1

13,3

14,4

a4

18,9

17,3

15,7

19,3

10,4

11,8

a5

15,7

17,8

12,0

18,9

17,6

17,0

Pj

0,19

0,11

0,12

0,23

0,22

0,13

 

a1=0,3   a2=0,8

 

17

N1

N2

N3

N4

N5

N6

a1

13,2

17,6

18,2

13,6

17,0

15,8

a2

8,7

19,9

17,3

18,3

18,0

14,8

a3

9,4

15,7

14,4

15,1

18,4

17,5

a4

11,6

12,4

17,6

15,7

17,3

15,3

a5

11,9

15,7

17,8

17,9

19,3

17,6

Pj

0,12

0,27

0,11

0,23

0,03

0,24

 

a1=0,4    a2=0,6

 

18

N1

N2

N3

N4

N5

N6

a1

13,4

15,5

14,6

15,5

18,4

13,4

a2

10,7

19,8

17,9

18,6

15,9

10,7

a3

13,2

17,6

18,3

14,5

16,9

13,2

a4

12,6

12,7

17,6

15,6

17,1

12,6

a5

15,0

13,3

17,8

17,7

19,6

15,0

Pj

0,12

0,19

0,31

0,23

0,03

0,12

 

a1=0,2    a2=0,8

 

19

N1

N2

N3

N4

N5

N6

a1

14,6

15,5

18,4

17,3

13,4

15,5

a2

17,6

15,6

17,1

15,7

12,6

12,7

a3

17,9

18,6

15,9

13,3

10,7

19,7

a4

17,8

15,5

19,1

17,6

15,0

13,3

a5

18,3

15,5

16,9

14,9

13,2

17,4

Pj

0,29

0,24

0,04

0,12

0,11

0,20

 

a1=0,9    a2=0,4

 

20

N1

N2

N3

N4

N5

N6

a1

15,0

15,5

17,1

17,6

17,8

13,0

a2

13,4

14,1

17,3

18,4

16,6

15,5

a3

12,6

15,6

15,7

17,1

17,6

12,7

a4

13,2

14,1

14,9

16,9

18,3

17,4

a5

10,7

18,6

13,3

15,9

17,9

14,7

Pj

0,15

0,05

0,12

0,34

0,20

0,14

 

a1=0,9   a2=0,5

 

21

N1

N2

N3

N4

N5

N6

a1

17,6

13,0

15,0

17,8

17,1

17,8

a2

18,4

15,5

13,3

16,6

17,3

14,2

a3

17,1

12,7

12,6

17,6

15,7

18,7

a4

17,1

14,7

12,6

17,6

15,7

14,1

a5

18,4

15,5

13,2

16,6

17,3

15,6

Pj

0,31

0,17

0,12

0,20

0,12

0,08

 

a1=0,8   a2=0,2

 

22

N1

N2

N3

N4

N5

N6

a1

17,1

17,1

13,0

17,8

16,8

17,6

a2

15,7

15,7

12,7

17,6

14,1

17,1

a3

17,3

15,6

13,4

16,6

18,4

15,6

a4

15,7

15,7

12,7

17,6

18,7

17,1

a5

17,3

15,5

13,4

16,6

18,4

14,2

Pj

0,12

0,12

0,17

0,20

0,08

0,31

 

a1=0,8    a2=0,4

 

Литература

 

1

Анфилатов В.С., Емельянов А.А., Кукушкин А.А., Системный анализ в управлении. Учебное пособие. – М.: Финансы и статистика, 2005.

2

Теория систем и системный анализ в управлении организациями / Под ред. В.Н. Волковой и А.А. Емельянова. – М.: Финансы и статистика, 2006.

3

Саати Т. Принятие решений. Метод анализа иерархий. – М.: Радио и связь, 1993

4

Т.Л.Партыка, И.И.Попов Математические методы – М., ФОРУМ – ИНФРА-М, 2005

5

Моудер Дж., Филлипс С. Метод сетевого планирования и организации работ (Перт) – М-Л,: Энергия 1966

6

Технологии принятия решений: метод анализа иерархий. ЗАО «Нейросплав» –http://data.mf.grsu.by/citforum/htdocs/consulting/BI/resolution/index.shtml

7

О. А. Ахметов, М. Б. Мжельский Метод анализа иерархий как составная часть методологии проведения оценки недвижимости ООО «Сибирский Центр Оценки», г.Новосибирск –http://www.nsk.su/~estate/articles/art001.html