4.6. Нелинейная парная корреляция

 

         Для изучения связи между признаками, которая выражается нелинейной функцией, используется более общий, чем коэффициент корреляции, показатель тесноты связи - корреляционное отношение.

         Нелинейная (или криволинейная) связь между двумя величинами - это такая связь, при которой равномерным изменениям  одной величины соответствует неравномерные изменения другой, причем эта неравномерность имеет определенный закономерный характер.

         Использование корреляционного отношения основано на разложении общей дисперсии зависимой переменной на составляющие: дисперсию, характеризующую влияние объясняющей переменной, и дисперсию, характеризующую влияние неучтенных и случайных факторов:

,

где

S²_у - общая дисперсия зависимой переменной, т.е. дисперсия относительно среднего значения;

S²_у|х - дисперсия функции регрессии относительно среднего значения зависимой переменной, характеризующая влияние объясняющей переменной;

S²_ост - дисперсия зависимой переменной у относительно функции регрессии, т.е.  остаточная дисперсия.

 

Корреляционной отношение выборочных данных определяется по формуле:

 

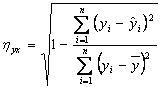
или .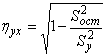

Влияние корреляционного отношения заключено в пределах:

 

.

Если дисперсия S²_y|x, обусловленная зависимостью величины у от объясняющей переменной х, равно общей дисперсии S²_y (а это возможно лишь при наличии функциональной связи), то h_yx=1. Если же остаточная (т.е. необъясненная) дисперсия S²_ост равна общей дисперсии S²_y, то h_yx=0, т.е. корреляционная связь отсутствует.

В предыдущей главе было отмечено,  что  линейный коэффициент парной  корреляции является симметричной функцией относительно х и у. Следует подчеркнуть, что этим свойством не обладает корреляционное отношение, т.е. h_xу¹h_yx. Для линейной связи h_xy=h_yx=r_xy Поэтому величину h²-r² можно использовать для характеристики нелинейности связи между переменными.

В качестве одного из самых простых критериев оценки нелинейности связи можно использовать следующий:

 

.

Если значение К_н>2,5, то корреляционную связь можно считать нелинейной.

Проверка и построение доверительных интервалов для корреляционного отношения генеральной совокупности осуществляются так же, как аналогичные процедуры для линейного коэффициента парной корреляции:

 

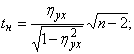
t_кр находится по таблице распределения Стьюдента из условия:

 

доверительный интервал имеет вид:

,

 

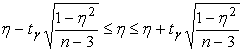где t_g находится по таблице интегральной функции Лапласа с учетом уровня доверительной вероятности g.

         Следует обратить внимание на то, что использование корреляционного отношения h имеет смысл только  для функций криволинейных, но линейных относительно параметров. Для функций, нелинейных относительно параметров [типа ], корреляционное отношение не может служить точным измерителем тесноты связи.

 

Тест

 

1. В каких пределах изменяется парный коэффициент корреляции?

а) 0 £  r_xy  £1;

б) -1 £r_xy  £ 1;

в) -¥£r_xy £ +¥;

г) 0 £r_xy £¥.

 

2. В каких пределах изменяется множественный коэффициент корреляции?

а) 0 £r_y|xz£ 1;

б) -1 £r_y|xz£ 1;

в) -¥£r_y|xz£+¥;

г) 0 £r_y|xz£¥.

 

3. Если парный коэффициент корреляции по модулю больше модуля соответствующего частного (например | r_xy|>| r_xy|z|) и коэффициенты не имеют разных знаков, то это означает, что:

а) фиксируемая переменная z ослабляет корреляционную связь;

б) фиксируемая переменная усиливает связь между х и у;

в) фиксируемая переменная не связана с факторами х и у;

г) возможен любой из первых трех исходов.

 

4. Коэффициент детерминации между х и у характеризует:

а) долю дисперсии у, обусловленную влиянием не входящих в модель факторов;

б) долю дисперсии у, обусловленную влиянием х;

в) долю дисперсии х, обусловленную влиянием не входящих в модель факторов;

г)направление зависимости между х и у.

 

5. Парный коэффициент корреляции между факторами равен 1. Это означает:

а) наличие нелинейной функциональной связи;

б) отсутствие связи;

в) наличие функциональной связи;

г) отрицательную линейную связь.

 

6. На основании 20 наблюдений выяснено, что выборочная доля дисперсии случайной величины у, вызванной вариацией х, составит 64%. Чему равен выборочный парный коэффициент корреляции:

а) 0,64;

б) 0,36;

в) 0,8;

г) 0,8 или -0,8.

 

7. По данным выборочного обследования группы предприятий было установлено, что выборочная доля дисперсии прибыли у, вызванная влиянием неучтенных в модели факторов, кроме фондовооруженности х, составляет 19%. Чему равен выборочный коэффициент детерминации:

а) 0,9;

б) -0,9;

в) 0,81;

г) 0,19.

 

8. По результатам  выборочных наблюдений были получены выборочные коэффициенты регрессии: b_yx=-0,5 и b_xy=-1,62. Чему равен выборочный парный коэффициент корреляции?

а) 0,81;

б) 0,9;

в) -0,9;

г) 0,19.

 

9. Частный коэффициент корреляции оценивает:

а) тесноту связи между двумя переменными при фиксированном значении остальных;

б) тесноту связи между двумя переменными;

в) тесноту связи между тремя переменными;

г) свободное влияние нескольких переменных на одну.

 

10. Множественный коэффициент корреляции оценивает:

 

а) долю дисперсии  одной переменной, обусловленную влиянием остальных переменных, включенных в модель;

б) степень совокупного влияния нескольких переменных на одну;

в) тесноту нелинейной связи между переменными;

г) тесноту связи между двумя переменными при фиксированном значении остальных.

 

 

К оглавлению

Назад к разделу "4.5. Ранговая корреляция"

Вперед к разделу "5. РЕГРЕССИОННЫЙ АНАЛИЗ"