Московская финансово-промышленная академия

 

 

 

 

 

 

 

 

 

 

Статистика

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Москва

2005

 

 

ТЕМА 1. ПРЕДМЕТ И МЕТОД СТАТИСТИКИ

 

Изучаемые статистикой явления и процессы многообразны.  В первую очередь, статистика изучает все, что связано с экономической деятельностью общества - производство и реализация промышленной и сельскохозяйственной продукции, строительство новых объектов и реконструкция действующих основных фондов, работа транспорта и связи, формирование и движение финансовых потоков. Статистические методы широко используются в анализе социальных процессов и явлений - занятости и безработицы, доходов населения, изучении общественного мнения и т.д. Большую роль играет статистика в технике и производственной деятельности, например, в организации контроля качества продукции. Методы статистики применяются в экономическом анализе, менеджменте, маркетинге, бизнес-планировании, логистике, оценке недвижимости, антикризисном управлении и в других областях научной и практической деятельности.

Что же означает термин «статистика»? В настоящее время насчитывается около тысячи определений статистики. Определять статистику как науку пытались философы, математики, экономисты, социологи, государственные деятели и, конечно, сами статистики. Сначала статистику определяли как «государствоведение», поскольку в основном она занималась описанием особенностей государств и служила для учета населения, сельскохозяйственных средств производства  для повышения эффективности взимания налогов и сборов, т.е. для реализации фискальных целей государств.  Постепенно, с развитием торговли и международных товарно-денежных отношений только описательной функции статистики становилось недостаточно и это послужило стимулом для развития аналитической функции статистики и формирования ее в самостоятельную науку.

 

В настоящее время под термином статистика чаще всего понимается следующее.

Статистика – это искусство и наука сбора и анализа данных.

 

 Поскольку данными называется любой вид зарегистрированной информации, статистика играет важную роль во всех сферах деятельности человека. Известный английский статистик У.Дж. Рейхман еще в начале прошлого века заметил:

«Едва ли не в каждом своем аспекте явления природы, а также человеческая и прочая деятельности подаются сейчас измерению при помощи статистических показателей».

Статистика – это одна из форм практической деятельности человека, цель которой – сбор, обработка и анализ данных о различных социальных, общественных и экономических явлениях.

Исторически данную функцию статистики реализует государство. Во всех странах мира  деятельностью по сбору  и обобщению статической информации для потребностей внутренней и внешней экономики занимаются специально учрежденные государствами органы – статистические комитеты и комиссии, статистические бюро. В нашем государстве эта работа выполняется Федеральной службой государственной статистики (прежнее название организации - Государственный комитет Российской Федерации по статистике). В задачу таких государственных и ведомственных органов также входит публикация данных как по стране в целом, например, в России издается Статистический ежегодник «Россия в цифрах», так и по отдельным регионам и отраслям экономики.

 

Статистикой называют также числовые (цифровые)  или количественные данные, характеризующие различные стороны жизни государства и общества: политические отношения, культуру, уровень жизни населения, развитие производства и т.п.

Но, прежде всего, статистика – это самостоятельная общественная наука, которая имеет свой предмет исследования и свои специфические методы.

 

Статистика - это наука, которая изучает количественную сторону массовых социально-экономических явлений и процессов в неразрывной связи с их качественной стороной, выявляет основные характеристики и закономерности развития этих явлений и процессов в конкретных условиях места и времени.

 

Из данного определения следуют основные особенности предмета статистики и статистики как науки.

       Предметом статистики является количественная сторона массовых качественно определенных социально-экономических явлений и процессов, отображаемых посредством статистически показателей.

            Каковы же особенности статистики как науки?

1. В отличие от других общественных наук статистика изучает количественную сторону общественных явлений. То есть статистика выявляет основные характеристики различных явлений общества и экономики, характеризует их, сравнивает между собой, анализирует происходящие с этими явлениями изменения, прежде всего, используя  числа или цифры.

 

2. Статистика изучает массовые явления.

Важной отличительной чертой статистики является ее нацеленность на выявление основных закономерностей, согласно которым развиваются изучаемые явления и объекты. Очевидно, что для того, чтобы установить закономерность развития процесса вцелом, необходимо проанализировать множество единичных случаев. Например, выявить, какая из двух групп колледжа лучше успевает в обучении невозможно, если взять по одному студенту из этих групп и сравнить полученные ими оценки. Для ответа на этот вопрос следует обобщить экзаменационные оценки всех студентов в каждой группе и сравнить полученные результаты. Поэтому статистика изучает не единичные факты, а массовые социально-экономические явления. При этом отдельные факты не игнорируются, а рассматриваются как составляющие общего явления. Например, изучая продолжительность жизни населения и смертность как общественные явления, статистика использует данные о количестве умерших и регистрирует в каком возрасте произошла смерть. Но установлением причины смерти в каждом конкретном случае занимается другая наука – медицина.

3. Для статистики исключительно важна качественная определенность используемых числовых данных.

Например, для математики действие 20+15=35 уже является результатом. А статистик, прежде чем сложить два этих числа обязательно бы  выяснил:

Ø      что характеризуют числа «20» и «15», это, например,  количество человек, работающих в одной бригаде, или прибыль предприятия за месяц?

Ø      какие единицы измерения имеют эти величины: например, если это прибыль предприятия, то она задана в тысячах или миллионах рублей? А если числа 20 и 15 имеют разные единицы измерения, например тысячи рублей и тонны, то их просто нельзя складывать, хотя арифметически, без учета их качественной определенности, это возможно.

Ø      к какому периоду времени относятся эти числа: например, это прибыль предприятия за март 2005 года и апрель 2005 года или это прибыль предприятия в декабре 2004 и в августе 2005?

Ø      является ли результат 35 реально значимой и имеющей смысл величиной, например, сложив декабрьскую прибыль 2004 года с прибылью августа 2005 года, никакого реального экономического смысла в полученном результате 35 не будет, но если сложить прибыли марта и апреля мы узнаем общую величину прибыли предприятия за два месяца.

 

1.2. Отрасли статистики

 

Статистика изучает различные аспекты жизни общества. В зависимости от специфики объекта исследования различают отдельные отрасли статистики (рис. 1.).

 

Рис.1 Отрасли статистики.

 

 

Теория статистики (общая теория статистики) – отрасль статистической науки, рассматривающая ее общие понятия, категории, принципы и методы сбора, обработки и анализа данных. Теорией статистики разрабатываются общие показатели и методы изучения структуры,  взаимосвязи и динамики социально-экономических процессов и явлений. Разрабатываемые теорией статистики методы и показатели используются другими отраслевыми статистиками.

Экономическая (макроэкономическая) статистика  изучает количественные закономерности происходящих в экономике явлений и процессов, выявляет основные тенденции экономического развития на макроуровне, т.е. на уровне крупного региона или страны в целом. Экономическая статистика изучает как сам процесс воспроизводства материальных благ и услуг, так и его результаты, а также их воздействие на уровень жизни населения. К основным показателям экономической статистики относятся валовой внутренний продукт, валовой региональный продукт, такие элементы национального богатства как основные фонды, материальные и оборотные средства, имущество домашних хозяйств.

В соответствии с классификацией отраслей экономики в статистической науке и практике также выделяется отраслевой уровень. К отраслевым статистикам относятся:

·статистика промышленности;

·статистика сельского хозяйства;

·статистика капитального строительства;

·статистика услуг, транспорта и связи;

·статистика торговли.

 

Статистика населения изучает численный и национальный состав, а также возрастно-половую структуру населения, его размещение и воспроизводство как  по стране в целом, так и в разрезе территориальных единиц. Одной из основных задач статистики населения является построение краткосрочных и долгосрочных демографических прогнозов.

Социальная статистика изучает социальную структуру населения, его уровень жизни и, в частности, доходы, а также уровень образования и культуры, состояния здоровья и медицинского обслуживания, использование свободного времени, общественное мнение, уровень преступности и другие социальные аспекты жизнедеятельности общества.

 

1.3. Метод статистики

 

Для того чтобы получить общее представление о статистической методологии, необходимо рассмотреть сам процесс статистического исследования, который включает четыре основных этапа.

1 этап. Процесс статистического исследования начинается с этапа сбора первичного статистического материала, проверки его полноты и достоверности. С этой целью применяются специальные методы, которые в  статистике называются методами статистического наблюдения. От качества полученных исходных данных во многом зависят окончательные результаты всего статистического исследования. 

2 этап. На втором этапе производится предварительная обработка данных. Собранную информацию необходимо упорядочить, систематизировать, т. е. подготовить для дальнейшей работы. Основной метод, используемый на данном этапе - метод группировок. В результате его реализации от больших массивов данных исследователь переходит к компактным и удобным для анализа статистическим таблицам.

3 этап. Расчет и интерпретация обобщающих статистических показателей. На данном этапе рассчитываются показатели среднего уровня и вариации, структуры, взаимосвязи и динамики изучаемых процессов и явлений. Полученные результаты подвергаются анализу.

4 этап. На четвертом этапе осуществляется моделирование взаимосвязей между социально-экономическими процессами и явлениями.

Используемые в процессе реализации всех этапов статистические приемы и методы в целом составляют методологию статистики.

 

1.4. Основные категории статистики.

 

Как любая наука, статистика имеет свой специфический язык, свои специальные термины, которые находятся в постоянном обиходе и постоянно используются при объяснении различных методов и других понятий. Перед тем, как приступить к изучению основных статистических показателей, приемов и методов статистического исследования, необходимо познакомиться с используемой в статистике терминологией, с основными категориями статистики.

 

К основным важнейшим категориям статистики относятся:

Ø      Признак;

Ø      Показатель;

Ø      Статистическая совокупность;

Ø      Единица статистической совокупности;

Ø      Вариация.

 

Важной категорией статистической науки является категория признака. Именно значения различных признаков наблюдаются и регистрируются на первой стадии статистического исследования - стадии статистического наблюдения.

Признак - это объективная характеристика какого-либо объекта или явления,  характерная черта или свойство, которое может быть определено или измерено.

Например, признаками, характеризующими промышленное предприятие, является выручка от реализации продукции, прибыль, стоимость основных фондов, численность персонала и др. Признаками человека являются возраст, пол, место жительства, профессия, среднемесячный доход и пр. Для любых окружающих нас объектов и явлений можно выделить достаточно большое число признаков, которые наблюдаются или потенциально могут наблюдаться в процессе статистического исследования.

Возможное значение, которое может принимать признак, называется вариантом. Например, существуют всего четыре варианта значений признака “экзаменационная оценка”: “2”, “3”, “4”, “5”. Если же учитывать оценки, проставляемые в зачетную книжку, то таких вариантов остается три, так как неудовлетворительная оценка в зачетку не проставляется. У отдельно взятого учащегося в зачетке могут быть и десять, и двадцать, и более значений признака “экзаменационная оценка”, но вариантов будет по-прежнему три, а возможно, два или один, если, например, студент или слушатель учится без троек и четверок.

Признаки подразделяются на количественные и качественные, а последние, в свою очередь, на альтернативные, атрибутивные и порядковые (рис. 2).

 

 

 

 

 

 

 

 

 


Рис. 2.  Классификация видов признаков

 

Количественным является признак, отдельные варианты которого имеют числовое выражение и отражают размеры, масштабы изучаемого объекта или явления. К количественным признакам, например, относятся доход домохозяйства, площадь жилого помещения, цена товара, стаж работы. Количественные признаки в статистике преобладают над другими видами признаков, они наиболее информативны, аналитичны, именно на работу с данными признаками нацелена большая часть многообразного статистического инструментария.

Количественные признаки разделяют на дискретные и непрерывные. Непрерывные признаки могут принимать любые числовые значения, например, прибыль предприятия может быть и положительной, причем от одного рубля до миллионов и триллионов рублей,  и отрицательной, и даже нулевой.

Дискретные признаки могут принимать значения, ограниченные определенным диапазоном, широта которого зависит от особенностей самого признака, например при изучении семей по числу детей типичными вариантами признака будут 0, 1, 2 и 3, хотя есть семьи, в которых растут и воспитываются и 4, и 5, и 10 и даже большее количество детей.

Качественные признаки, в отличие от количественных, не поддаются прямому числовому описанию. Они характеризуют различные  свойства объектов и явлений, отражают их состояние или отдельные характеристики. Например, к качественным признакам относятся форма собственности предприятия, пол человека, уровень образования, квалификация специалиста и др.

Альтернативным называется качественный признак, имеющий только два варианта значений. Например, продукция предприятия может соответствовать предъявляемым требованиям или быть бракованной, пол человека может быть мужским или женским, население страны или региона обычно делится на городское и сельское.

Альтернативный признак может иметь и числовое выражение. Предположим, при анкетировании потребителей вопрос о доходах в анкете предполагал всего два варианта: “до 5 тыс. рублей в месяц” и “5 тыс. рублей в месяц и более”. В этом случае количественный признак был преобразован в альтернативный.

В отличие от альтернативного атрибутивный признак имеет  более двух вариантов, которые при этом выражаются в виде понятий или наименований. К атрибутивным признакам относятся район проживания, вид продукции, специальность работника, цвет товара. Такие признаки имеют место в различных областях исследования, но в большей степени они характерны для информации, с которой работают маркетологи, социологи и психологи.

Порядковые признаки отличаются от атрибутивных тем, что они имеют несколько ранжированных, т.е. упорядоченных по возрастанию или убыванию, качественных вариантов. Примерами таких признаков являются уровень образования (начальное, общее среднее и т.д.), уровень квалификации, воинское звание, различного рода рейтинги. Отдельные варианты порядкового признака трудно соизмерить количественно. Например, понятно, что образованность человека с высшим образованием выше, чем со средним специальным, но при этом нельзя утверждать, что она выше на 20% или на 30%. Водительская категория “Е” выше, чем водительская категория “В”, но количественных пропорций между ними не существует.

Следует отметить, что порядковый признак может иметь числовое выражение. В качестве примеров можно привести такие порядковые признаки как разряд рабочего, тарифный разряд служащего, рейтинговые оценки, экзаменационные оценки. Школьник, получивший четверку, не обязательно продемонстрировал ровно в два раза больше знаний по сравнению со школьником, получившим двойку. Рабочий 6-го разряда не обязательно в два раза больше вырабатывает продукции и в два раза больше зарабатывает по сравнению с рабочим 3-го разряда. В обозначении вариантов этих признаков цифры можно заменить буквами алфавита без какого-либо снижения их информативности.

Как вы уже знаете, статистика изучает социально-экономические явления комплексно. Поэтому, приступая к исследованию социальных или экономических процессов, статистика объединяет отдельные объекты или явления в специальные группы, которые называются статистическими совокупностями.

Статистическая совокупность - это реально существующее множество объектов или явлений, объединенных общими признаками и обладающих внутренней взаимосвязью и целостностью.  Статистика имеет дело с совокупностями промышленных, сельскохозяйственных, строительных и торговых предприятий, с совокупностью коммерческих банков, с совокупностью населения страны или отдельного ее региона. Так, например, всех жителей г. Москвы можно рассматривать как статистическую совокупность, так как один признак - город проживания - будет у всех одинаковым. По остальным же признакам - полу, возрасту, социальному положению - население будет отличаться.

Индивидуальный объект или явление, составляющее статистическую совокупность, называется единицей статистической совокупности.

При проведении исследования именно у единиц совокупности измеряются или фиксируются важные для исследования признаки. Для отрасли единицей совокупности будет являться отдельное предприятие, для банковской системы - отдельный банк. В некоторых случаях для одной и той же совокупности можно выделить разные группы единиц. Например, при изучении половозрастной структуры населения единицей является отдельный человек, при изучении же доходов, обеспеченности жильем, предметами длительного пользования (телевизоры, холодильники и т.п.) единицей будет являться домохозяйство.

Общее число единиц, образующих статистическую совокупность, называется объемом совокупности.

Объем совокупности следует отличать от объема признака,  т.е. суммарного значения признака по всем единицам изучаемой совокупности. Так, например, число предприятий в отрасли - это объем совокупности, а общий выпуск продукции на всех предприятиях отрасли - это объем признака. В некоторых случаях объем признака не имеет реального экономического смысла, например, трудно интерпретировать суммарный рост всех студентов одной группы. Но для расчета отдельных статистических показателей, в частности - средних, такое суммирование необходимо.

Одной из важнейших характеристик статистической совокупности является ее однородность. Однородной является совокупность, единицы которой близки между собой по значениям признаков, существенных для данного исследования. Многие методы и приемы статистического исследования применимы лишь к однородным совокупностям.

Вы уже обратили внимание, что внутри статистической совокупности отдельные объекты и явления могут сильно отличаться друг от друга по своим свойствам и характеристикам, то есть по тем признакам, которые не являются общими и одинаковыми для всех  единиц данной совокупности.  Например, у единиц совокупности «Население г. Москвы» есть один общий (одинаковый для всех) признак – город проживания, и множество признаков, по которым единицы совокупности – москвичи – отличаются друг от друга: пол, возраст, уровень образования, заработная плата или доход и множество других. 

На языке статистики описанный выше пример звучал бы следующим образом: население Москвы варьирует по полу, возрасту, уровню образования, доходу и другим признакам. Или иначе: внутри совокупности «Население г. Москвы» существует вариация признаков «пол», «возраст», «уровень образования» и «доход».

Вариация – это изменяемость, колеблемость величины признака у различных единиц совокупности, т.е. принятие единицами совокупности разных вариантов значений признака.

Что является причиной такой изменчивости?

Во-первых, индивидуальные особенности изучаемых объектов.

Например, коммерческие банки варьируют по величине активов в зависимости от размера уставного фонда и реализуемой финансовой политики,   работники предприятия имеют разную производительность труда в зависимости от их квалификации и мотивации, но также на производительность труда влияют состояние здоровья, настроение работника, текущее положение дел на предприятии и общая атмосфера в трудовом коллективе. 

Во-вторых, изменяемость происходит под воздействием определенных условий, в том числе и форс-мажорных.

Например, вариация городов по численности населения зависит от географического положения города, развитости городской инфраструктуры и экономического положения в регионе. Спрос на туристические поездки в Таиланд в начале 2005 года значительно снизился после разрушений, вызванных Цунами, что отразилось на выручке туристических операторов, организующих отдых в этой стране.   

Именно наличие вариации и изменчивость данных определяет необходимость статистики как науки и делает неизбежным процесс постоянного отслеживания и анализа информации о том, как развивается общество и экономика, как работает та или иная отрасль промышленности, насколько эффективно функционирует конкретное предприятие.

Большую роль в статистическом исследовании играет закон больших чисел – общий принцип, в силу которого количественные закономерности, присущие массовым явлениям, отчетливо проявляются лишь при достаточно большом числе наблюдений. Единичные явления в большей степени подвержены действию случайных и несущественных факторов, чем масса в целом. При большом числе наблюдений случайные отклонения в ту или иную сторону от общей закономерности развития взаимно погашаются.  В результате взаимопогашения случайных отклонений обобщающие показатели, исчисленные для величин одного и того же вида, становятся типичными, отражающими действие постоянных и существенных факторов в данных условиях места и времени.

Статистическое исследование независимо от его масштабов и целей всегда завершается расчетом и анализом различных по виду и форме выражения статистических показателей.

Статистический показатель представляет собой количествен­ную характеристику социально-экономических явлений и процессов в условиях качественной определенности. Качественная определенность показателя заключается в том, что он непосредственно связан с внутренним содержанием изучаемого явления или процесса, его сущностью.

Как правило, изучаемые статистикой процессы и явления достаточно сложны, и их сущность не может быть отражена посредством одного отдельно взятого показателя. В таких случаях используется система статистических показателей.

Система статистических показателей - это совокупность взаимосвязанных показателей, имеющая одноуровневую или многоуровневую структуру и нацеленная на решение конкретной статистической задачи. Так, например, сущность промышленного предприятия заключается в производстве какой-либо продукции на базе эффективного использования средств производства и трудовых ресурсов. Следовательно, для полной экономической характеристики работы предприятия необходимо использовать систему показателей, в число которых входят величина прибыли, общий объем производства или общая стоимость оказанных услуг, численность персонала, производительность труда, величина основных фондов и их состояние  и др.

В отличие от признака статистический показатель получается расчетным путем. Это могут быть простой подсчет единиц совокупности, суммирование их значений признака, сравнение двух или нескольких величин, а также более сложные расчеты.

Различают конкретный статистический показатель и показатель-категорию.

Конкретный статистический показатель характеризует размер, величину изучаемого явления или процесса в данном месте на конкретной территории или у конкретного объекта в данное время. Так, если мы называем конкретную величину стоимости промышленно-производственных фондов, то обязательно должны указать, к какому предприятию или отрасли и к какому моменту времени она относится.

Показатель-категория отражает сущность, общие отличительные свойства конкретных статистических показателей одного и того же вида без указания места, времени и числового значения. Например, показатели розничного товарооборота предприятий торговли и общественного питания в Москве и Санкт-Петербурге в 2000 и 2003 гг. отличаются местом, временем и конкретными числовыми значениями, но имеют одну и ту же сущность (продажа товаров через розничную торговую сеть и сеть предприятий общественного питания), которая отражена в названии данного показателя-категории.

Все статистические показатели по охвату единиц совокупности разделяются на индивидуальные и сводные (рис. 3).

 

 

 

 

 


Рис. 3. Классификация показателей по охвату единиц совокупности

 

Индивидуальные показатели характеризуют отдельный объект или отдельную единицу совокупности - предприятие, фирму, банк, домохозяйство и т. п. Примером индивидуальных абсолютных показателей может служить численность промышленно-производственного персонала предприятия, оборот торговой фирмы, совокупный доход домохозяйства.

На основе соотнесения двух индивидуальных абсолютных показателей, характеризующих один и тот же объект или единицу, получают индивидуальный относительный показатель. В статистике рассчитываются и индивидуальные средние показатели, но только во временном измерении (среднегодовая численность промышленно-производственного персонала предприятия).

Сводные показатели в отличие от индивидуальных характеризуют группу единиц, представляющую собой часть статистической совокупности или всю совокупность в целом. Эти показатели, в свою очередь, подразделяются на объемные и расчетные

Объемные показатели получают путем сложения значений признака отдельных единиц совокупности. Полученная величина, называемая объемом признака, может выступать в качестве объемного абсолютного показателя (например, стоимость основных фондов предприятий отрасли), а может сравниваться с другой объемной абсолютной величиной (например, с численностью промышленно-производственного персонала этих предприятий) или объемом совокупности (в данном примере- с числом предприятии). В последних двух случаях получают объемный относительный и объемный средний показатели (в наших примерах - фондовооруженность и средняя стоимость основных фондов).

Расчетные показатели, вычисляемые по различным формулам, служат для решения отдельных статистических задач анализа - измерения вариации, характеристики структурных сдвигов, оценки взаимосвязи и т. д. Они также делятся на абсолютные, относительные или средние. В эту группу входят индексы, коэффициенты тесноты связи, ошибки выборки и прочие показатели, подробно рассмотренные в соответствующих главах.

Охват единиц совокупности и форма выражения являются основными, но не единственными классификационными признаками статистических показателей. Важным классификационным признаком является также временной фактор. Социально-экономические процессы и явления находят свое отражение в статистических показателях либо по состоянию на определенный момент времени, как правило, на определенную дату, начало или конец месяца, года (численность населения, стоимость основных фондов, дебиторская задолженность), либо за определенный период - день, неделю, месяц, квартал, год (производство продукции, число заключенных браков, сумма страховых выплат). В первом случае показатели являются моментными, во втором - интервальными.

С точки зрения пространственной определенности статистические показатели подразделяются на общетерриториальные, характеризующие изучаемый объект или явление в целом по стране, региональные и местные (локальные), относящиеся к какой-либо части территории или отдельному природному объекту.

 

ТЕМА 2. МЕТОДЫ СБОРА И СИСТЕМАТИЗАЦИИ СТАТИСТИЧЕСКОЙ ИНФОРМАЦИИ. СВОДКА И ГРУППИРОВКА ДАННЫХ

 

2.1. Статистическая сводка данных

 

Важнейшим этапом исследования социально-экономических явлений и процессов является систематизация первичных данных, собранных по итогам наблюдения.

Представьте, что перед Вами поставлена задача изучить деятельность всех  промышленных предприятий текстильной отрасли России по четырем признакам: численность промышленно-производственного персонала, объем выпуска продукции, величина прибыли и размер основных фондов.

Даже если ввести информацию по каждому предприятию в обычную таблицу Excel и распечатать полный перечень предприятий, Вы получите несколько страниц с колонками данных, анализировать которые в таком виде будет крайне затруднительно. Во-первых, потому что данные неупорядочены и показатели предприятий-гигантов будут в таком списке соседствовать с показателями небольших текстильных фабрик. Это неизбежно вызовет разницу в значимости самих данных: трехзначные показатели небольших предприятий будут сильно отличаться от миллионных величин предприятий-лидеров отрасли. Во-вторых, крупные и малые предприятия имеют свои отличительные особенности как в организации производства, так и по возможностям реализации продукции, поэтому сравнивать полученные ими показатели не совсем верно, и правильнее изучать и сравнивать экономические показатели крупных, средних и малых предприятий отдельно по обозначенным группам.

Именно поэтому собранную статистическую информацию необходимо хорошо подготовить к последующим обработке и анализу.

 

Для этого статистика применяет два основных метода:

Ø      Метод сводки;

Ø      Метод группировки.

 

Сводка - это научная обработка первичных данных с целью получения обобщенных характеристик изучаемого социально-экономического явления по ряду существенных для него признаков.

По глубине и точности обработки информации различают сводку простую и сложную.

 

 

 

 

 

 

 

 

 

 


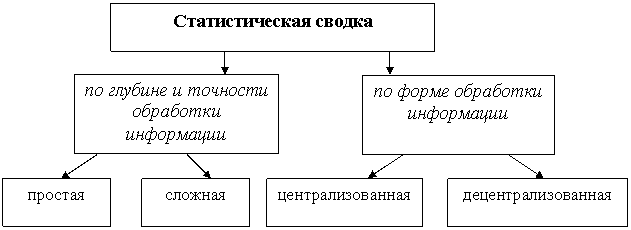
Рис. 2.1. Виды статистической сводки.

 

Простая сводка - это операция по подсчету общих итогов по совокупности единиц наблюдения и оформление этого материала в статистических таблицах.

Сложная сводка -  это комплекс последовательных операций, включающих группировку данных, составление системы показателей для характеристики выделенных групп, подсчет числа единиц и итогов по каждой группе и по всей совокупности и представление результатов в виде статистических таблиц.

Проведение сводки включает следующие этапы:

-     выбор группировочного признака – признака, по значениям которого единицы совокупности будут делиться на группы (например, по численности промышленно-производственного персонала можно выделить 3 группы предприятий: до 100 человек, от 100 до 300 человек и свыше 300 человек);

-     определение порядка формирования групп;

-     разработка системы статистических показателей для характеристики групп и объекта в целом;

-     разработка макетов статистических таблиц для представления результатов сводки.

По форме обработки материала сводка бывает:

-     централизованная, когда весь первичный материал поступает в одну организацию, подвергается в ней обработке от начала до конца;

-     децентрализованная, когда отчеты предприятий сводятся статистическими органами субъектов РФ, а полученные итоги поступают в федеральную службу по статистике и там определяются итоговые показатели в целом по народному хозяйству страны.

 

2.2.  Виды статистических группировок

 

Группировкой называется разбиение общей совокупности единиц объекта наблюдения по одному или нескольким существенным признакам на более однородные группы. Группы могут различаться между собой по числу объектов и в качественном отношении. Группировка является важнейшим статистическим методом обобщения статистических данных, основой для правильного исчисления статистических показателей.

Метод группировок позволяет решать следующие задачи:

·      выделять социально-экономические типы явлений;

·      изучить структуру явления;

·      выявить взаимосвязи и взаимозависимости между явлениями.

В соответствии с познавательными задачами, решаемыми в ходе построения статистических группировок, различают следующие их виды: типологические, структурные, аналитические.

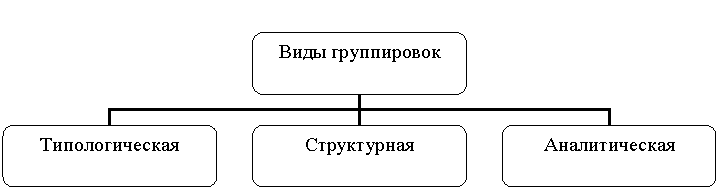
Организационная диаграмма

Рис. 2.2. Виды группировок.

 

Типологическая группировка - это разбиение разнородной совокупности единиц наблюдения на отдельные качественно однородные группы и выявление на этой основе социально-экономических типов явлений.

Примером типологической группировки является группировка предприятий и организаций по формам собственности (табл. 2.1).

 

Таблица2.1.

Группировка предприятий и организаций по формам собственности в России (на январь 2001 г.)

 

№ п/п

Группы предприятий по формам собственности

Число предприятий

Всего, тыс.

% к итогу

 

А

1

2

1

Государственная

151

4,5

2

Муниципальная

217

6,5

3

Частная

2510

75,0

4

Собственность общественных и религиозных организаций (объединений)

223

6,7

5

Прочие формы собственности, включая смешанную российскую, иностранную, совместную российскую и иностранную

247

7,3

 

Всего

3346

100,0

 

В результате такой группировки из всей совокупности были выделены 5 относительно устойчивых групп или типов предприятий и организаций в зависимости от их формы собственности. Каждая группа предприятий имеет свои специфические особенности по учету хозяйственных операций, налогообложению, подчиненности и др.

Но, обратившись к таблице 3.1., можно легко сделать выводы по данной совокупности в целом: подавляющее большинство предприятий находится в частной собственности – 75%; предприятия государственной собственности составили 4,5%; предприятия муниципальной собственности – 6,5%; в собственности общественных объединений и прочих форм собственности находится 6,7% предприятий.

Структурной называется группировка, которая предназначена для изучения состава однородной совокупности по какому-либо варьирующему признаку.

Примером структурной группировки по количественному признаку является группировка крестьянских хозяйств по размеру земельного участка (табл. 2.2).

Таблица 2.2.

Группировка крестьянских хозяйств по размеру

 земельного участка в Ярославской области (по состоянию на 1 января 2000 г.)

 

Группы хозяйств с площадью земли, га

Число хозяйств

Площадь земли

единиц

% к итогу

га

% к итогу

А

1

2

3

4

Земля не предоставлялась

16

0,8

-

-

До 3

179

8,6

405

0,9

4-10

805

38,6

5744

12,9

11-20

484

23,2

8018

18,0

21-70

486

23,3

17936

40,3

71-100

72

3,4

5587

12,5

101-200

38

1,8

5071

11,4

201 и выше

6

0,3

1768

4,0

Итого

2086

100,0

44529

100,0

 

Данные табл. 3.2 показывают, что 38,6% крестьянских хозяйств имеют земельный участок размером 4-10 га, и им принадлежит всего около 13% земельной площади. Доли следующих двух групп составляют соответственно 23,2 и 23,3%. Именно этим крестьянским хозяйствам принадлежит около 40,3% земли. Число хозяйств в группах 101-200 га и 201 и выше составляет всего лишь 2,1% им принадлежит 15,4% земли (11,4+4,0).

Группировка, выявляющая взаимосвязи между изучаемыми явлениями и  признаками, их характеризующими, называется аналитической группировкой.

В статистике при изучении связей социально-экономических явлений признаки необходимо делить на факторные и результативные.

Факторными называются признаки, под воздействием которых изменяются другие результативные признаки. Взаимосвязь проявляется в том, что с возрастанием или убыванием значения факторного признака систематически возрастает или убывает значение признака результативного и наоборот.

При построении аналитической группировки, как правило:

·      единицы совокупности группируются по факторному признаку;

·      каждая выделенная группа характеризуется средними величинами результативного признака.

Пример аналитической группировки представлен в табл. 2.3.

 

Таблица 2.3.

Группировка зависимости суммы кредитов, выданных коммерческими банками,  от размера процентной ставки

 

№ п/п

Группы банков по величине процентной ставки

Число банков

Сумма выданных кредитов,

млн. руб.

всего

в среднем на один банк

 

А

1

2

3

1

11-15

7

168,1

24,0

2

15-19

13

200,5

15,4

3

19-23

7

54,4

7,8

4

23-27

3

6,8

2,3

 

Итого

30

429,8

14,3

 

 

Данные табл. 3.3 показывают, что с ростом процентной ставки, под которую выдается кредит, средняя сумма кредита, выдаваемая одним банком, уменьшается! Это говорит о том, что между исследуемыми признаками существует обратная связь.

По способу построения группировки бывают простые и комбинационные.

Простой называется группировка, в которой группы образованы только по одному признаку.

Комбинационной называется группировка, в которой разбиение совокупности на группы производится по двум и более признакам, взятым в  сочетании (комбинации).

Сначала группы формируются по одному признаку, затем группы делятся на подгруппы по другому признаку, а эти в свою очередь делятся по третьему и так далее. Таким образом, комбинационные группировки дают возможность изучить единицы совокупности одновременно по нескольким взаимосвязанным признакам.

Примером комбинационной группировки является группировка коммерческих банков по величине кредитных вложений  и объему вложений в ценные бумаги, представленная в табл. 2.4.

Таблица2.4.

Группировка коммерческих банков по величине кредитных вложений и объему вложений в ценные бумаги в одном из регионов

№

 п/п

Группы коммерческих банков

 по величине

кредитных вложений, млн руб.

Подгруппы по объему

вложений в ценные бумаги, млн руб.

Число

банков

1

до 52

до 108

108-160

более 160

10

10

-

 

Итого по группе

 

20

2

52-104

до 108

108-160

более 160

41

11

10

 

Итого по группе

 

62

3

104-156

до 108

108-160

более 160

55

-

11

 

Итого по группе

 

66

 

ВСЕГО

 

148

 

При построении комбинационной группировки возникает вопрос о последовательности разбиения единиц объекта по признакам. Как правило, рекомендуется сначала производить группировку по качественным признакам, а затем по количественным. Например, в группировке водителей автопарка по уровню квалификации и производительности труда, вначале все водители делятся на две группы по классу – качественному признаку, а затем внутри каждого класса производится деление по проценту выполнения плана – количественному признаку (табл. 2.5.).

Таблица 2.5.

Группировка водителей автопарка по уровню квалификации и производительности труда

 

Квалификация водителя

% выполнения

плана

Количество

водителей,

чел.

Средний размер заработанной платы,

тыс. руб.

I класс

100-110

110 и более

5

8

14,8

16,3

Итого по группе

-

13

-

II класс

100-110

110 и более

7

10

13,7

14,5

Итого по группе

-

17

-

ВСЕГО

-

30

-

 

 

2.3. Принципы построения статистических группировок и классификаций

 

Построение статистических группировок осуществляется по следующим этапам:

1.       Определение группировочного признака.

2.       Определение числа групп.

3.       Расчет ширины интервала группировки.

4.       Определение признаков, которые в комбинации друг с другом будут характеризовать каждую выделенную группу.

 

Построение группировки начинается с определения группировочного признака.

Группировочным признаком называется признак, по которому проводится разбиение единиц совокупности на отдельные группы. От правильного выбора группировочного признака зависят выводы статистического исследования. Группировочный признак часто называют основанием группировки.

В основание группировки могут быть положены как количественные, так и качественные признаки.

После того, как определено основание группировки следует решить вопрос о количестве групп, на которые необходимо разбить исследуемую совокупность единиц наблюдения.

Число групп зависит от вида показателя, положенного в основание группировки, объема изучаемой совокупности и степени вариации признака.

Вид показателя особенно существенен при анализе качественных признаков.

Если группировочный признак качественный, то число групп будет равно числу вариантов этого признака.

Например, группируя сотрудников фирмы по полу, мы получим две группы: сотрудники-мужчины и сотрудники-женщины. Группируя предприятия по форме собственности, мы получим 5 групп по числу вариантов признака «форма собственности»: государственные предприятия, частные, муниципальные, общественных объединений, смешанной формы собственности.

В случае группировки единиц наблюдения по количественному признаку особое внимание необходимо обратить на число единиц исследуемого объекта, т.е. на объем совокупности и степень колеблемости группировочного признака.

При небольшом объеме совокупности (n<50) не следует образовывать большого количества групп, так как группы будут включать недостаточное число единиц объекта. Показатели, рассчитанные для таких групп, не будут представительными и не позволят получить адекватную характеристику исследуемого явления.

Часто группировка по количественному признаку имеет задачу отразить распределение единиц совокупности по этому признаку. В этом случае количество групп зависит, в первую очередь, от степени колеблемости группировочного признака: чем больше его колеблемость, тем больше можно образовать групп. Поэтому при определении числа групп необходимо принять во внимание размах вариации признака (R), который позволяет оценить общие границы вариации признака в данной совокупности.

R  определяется по следующей формуле:

 

R = хmax – хmin  ,                                                      (2.1)

где

Х max – максимальное значение группировочного признака,

Х min – минимальное значение группировочного признака в данной совокупности.

 

Чем больше размах вариации признака, положенного в основание группировки, тем, как правило, большее число групп может быть образовано.  При этом может возникнуть проблема получения пустых групп, т.е. групп, не содержащих ни одной единицы наблюдения.

Построение большого числа групп позволит, с одной стороны, точнее воспроизвести характер исследуемого объекта. Однако, с другой стороны, слишком большое число групп затрудняет выявление закономерностей при исследовании социально-экономических явлений и процессов. Поэтому в каждом конкретном случае при определении числа групп следует исходить не только из степени колеблемости признака, но и из особенностей объекта и показателей, его характеризующих  а также цели исследования.

Определение числа групп можно осуществить несколькими способами. Формально-математический способ предполагает  использование формулы Стерджесса:

 

m = 1 + 3,322 ´ lg n,                                                 (2.2)

 

где      m - число групп

            n - число единиц совокупности.

 

Согласно этой формуле выбор числа групп зависит только от объема изучаемой совокупности.

Применение данной  формулы  дает хорошие результаты в том случае, если совокупность состоит из большого числа единиц наблюдения (n>50).

Когда определено число групп, то следует определить интервалы группировки.

Интервал - это значения варьирующего признака, лежащие в определенных границах. Каждый интервал имеет верхнюю и нижнюю границы или одну из них. Нижней границей интервала называется наименьшее значение признака  в интервале.  Верхней границей интервала называется наибольшее значение признака в интервале. Ширина интервала представляет собой разность между верхней и нижней границами интервала.

Интервалы группировки бывают:

Ø      равные (одинаковые) по ширине и неравные по ширине;

Пример группировки с равными интервалами представлен в табл. 2.6.

                  Таблица 2.6.

Группы коммерческих банков по величине балансовой прибыли

Номер группы

Балансовая прибыль,

млн. руб.

Число банков, ед.

Ширина каждого интервала одинакова и составляет 200 млн. руб.

1

2

3

200 - 400

400 - 600

600 - 800

40

40

20

400-200=200

600-400=200

800-600=200

 

Итого

100

 

 

Пример группировки с неравными интервалами представлен в таблице 2.7.

                                                                        

             Таблица 2.7.

Группы фирм по объему инвестиций

Номер группы

Объем инвестиций,

млн. руб.

Число фирм

Ширина интервалов в данной группировке не является одинаковой

1

2

3

10-20

20-40

40-80

5

10

8

20-10 = 10 млн. руб.

40-20 = 20 млн. руб.

80-40 = 40 млн. руб.

4

  80-100

4

          100-80 = 20 млн. руб.

 

Итого

37

 

 

 

Равные интервалы применяются в случае, если изменение количественного признака внутри изучаемой совокупности единиц наблюдения происходит равномерно и его вариация проявляется в сравнительно узких границах.

Ширина равного интервала определяется по следующей формуле:

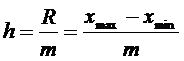                                                            (2.3)

где     

хmax, xmin - максимальное и минимальное значения признака в совокупности;

m - число групп.

 

Если максимальные или минимальные значения сильно отличаются от других значений группировочного признака, то для определения ширины интервала следует использовать не максимальное или минимальное значения, а значения, несколько превышающие минимум, и несколько меньше, чем максимум.

Полученную по формуле (2.3) величину округляют и используют в качестве ширины интервала.

 

Существуют следующие правила округления ширины интервала.

Ø                       Если ширина интервала, рассчитанная по формуле (2.3) представляет собой величину, которая имеет один знак до запятой (например: 0,67; 1,487; 3,82), то в этом случае полученные значения округляют до десятых. В приведенном выше примере это будут соответственно значения: 0,7; 1,5; 3,8.

Ø      Если рассчитанная ширина интервала имеет две значащие цифры до запятой и несколько после запятой (например, 14,876), то это значение необходимо округлить до целого числа (до 15).

Ø      В случае, когда рассчитанная ширина интервала представляет собой трехзначное, четырехзначное или еще большее по значимости число, то эту величину следует округлить до ближайшего числа, кратного 100 или 50. Например, 652 следует округлить до 650 или до 700.

 

Интервалы группировки бывают также:

Ø      открытыми  и закрытыми.

 

Закрытыми  называются интервалы, у которых имеются обе границы: верхняя и нижняя границы (табл. 2.8.)

 

Таблица 2.8.                                                   Таблица 2.9.

Пример группировки с закрытыми                  Пример группировки с открытыми

интервалами                                                            первым и  последним интервалами

 

 

 

 

Прибыль предприятий, млн. руб.

Число предприятий

 

Прибыль предприятий,

млн. руб.

Число предприятий

20 - 40

40 - 60

60 - 80

 80 - 100

5

15

20

10

 

до 40

40 - 60

60 - 80

80 и выше

5

15

20

10

 








 

 

 

Открытые - это интервалы, у которых указана только одна граница: как правило, верхняя - у первого интервала и  нижняя - у последнего.

Например, группы страховых компаний по величине прибыли (млн. руб.): до 40, 40-60, 60-80, 80 и выше. Применение открытых интервалов целесообразно в тех случаях, когда в совокупности встречается незначительное число единиц наблюдения с очень малыми или очень большими значениями вариантов, которые резко, в несколько раз, отличаются от всех остальных значений  изучаемого признака.

При группировке единиц совокупности по количественному признаку границы интервалов могут быть обозначены по-разному, в зависимости от того, непрерывный  или дискретный признак положен в основание группировки.

Если основанием группировки служит непрерывный признак (например, группы строительных фирм по объему строительно-монтажных работ, выполненных собственными силами  (тыс. руб.): 1200-1400, 1400-1600, 1600-1800, 1800-2000), то одно и то же значение признака выступает и верхней и нижней границами двух смежных интервалов. В данном случае объем работ 1400 тыс. руб. составляет верхнюю границу первого интервала и нижнюю границу второго, 1600 тыс. руб. - соответственно второго и третьего и т.д., то есть верхняя граница i - го интервала равна нижней границе (i+1) - го интервала.

При таком обозначении границ может возникнуть вопрос, в какую группу включать единицы наблюдения, значения признака у которых совпадают с границами интервалов. Например, во вторую или третью группу должна войти строительная фирма с объемом строительно-монтажных работ 1600 тыс. рублей? Если верхняя граница формируется по принципу «исключительно», то фирма должна быть отнесена к третьей группе, в противном случае - ко второй. Для того, чтобы правильно отнести к той или иной группе единицу совокупности, значение признака которой совпадает с границами интервалов, можно ориентироваться на открытые интервалы (по нашему примеру группы строительных фирм по объему строительно-монтажных работ преобразуются в следующие: до 1400, 1400-1600, 1600-1800, 1800 и более). В данном случае, вопрос отнесения отдельных единиц совокупности, значения которых являются граничными, к той или иной группе решается на основе анализа последнего открытого интервала. Возможны два случая обозначения последнего открытого интервала: 1).1800 тыс. руб. и более; 2). более 1800 тыс. руб. В первом случае, строительные фирмы с объемом строительно-монтажных работ 1600 тыс. руб. попадут в третью группу; во втором случае - во вторую группу.

Если в основании группировки лежит дискретный признак, то нижняя граница i-го интервала равна верхней границе i-1-го интервала, увеличенной на 1. Например, группы строительных фирм по числу занятого персонала (чел.) будут иметь вид: 100-150, 151-200, 201-300.

 

Пример.

Произведем группировку единиц совокупности, включающей 30 банков Российской Федерации (на 01.01.04 г.):

 

Номер

банка

Капитал,

млн. руб.

Рабочие

активы, млн. руб.

Уставный

фонд, млн. руб.

1

207,7

2,48

1,14

2

200,3

2,40

1,10

3

190,2

2,28

1,05

4

323,0

3,88

1,88

5

247,1

2,96

1,36

6

177,7

2,12

0,97

7

242,5

2,90

1,33

8

182,9

2,18

0,99

9

315,6

3,78

1,73

10

183,2

2,20

1,01

11

320,2

3,84

1,76

12

207,3

2,48

1,14

13

181,0

2,17

0,99

14

172,4

2,06

0,94

15

234,3

2,81

1,29

16

189,5

2,27

1,04

17

187,8

2,24

1,03

18

166,9

1,99

0,91

19

157,7

1,88

0,86

20

168,3

2,02

0,93

21

224,4

2,69

1,23

22

166,5

1,99

0,91

23

198,5

2,38

1,09

24

240,4

2,88

1,32

25

229,3

2,75

1,26

26

175,2

2,10

0,96

27

156,0

1,87

0,86

28

160,1

1,92

0,88

29

178,7

2,14

0,98

30

171,6

2,05

0,94

           

 

В качестве группировочного  признака возьмем капитал банка. Образуем четыре группы банков с равными интервалами. Для удобства расчетов преобразуем таблицу исходных данных и расположим банки по убыванию величины капитала (табл. 2.10).

 

Таблица 2.10.

Показатели деятельности 30  банков РФ (на 01.01.04)

 

Номер

банка

Капитал,

млн. руб.

Рабочие

активы,

млн. руб.

Уставный

фонд,

млн. руб.

4

323,0

3,88

1,88

11

320,2

3,84

1,76

9

315,6

3,78

1,73

5

247,1

2,96

1,36

7

242,5

2,90

1,33

24

240,4

2,88

1,32

15

234,3

2,81

1,29

25

229,3

2,75

1,26

21

224,4

2,69

1,23

1

207,7

2,48

1,14

12

207,3

2,48

1,14

2

200,3

2,40

1,10

23

198,5

2,38

1,09

3

190,2

2,28

1,05

16

189,5

2,27

1,04

17

187,8

2,24

1,03

10

183,2

2,20

1,01

8

182,9

2,18

0,99

13

181,0

2,17

0,99

29

178,7

2,14

0,98

6

177,7

2,12

0,97

26

175,2

2,10

0,96

14

172,4

2,06

0,94

30

171,6

2,05

0,94

20

168,3

2,02

0,93

18

166,9

1,99

0,91

22

166,5

1,99

0,91

28

160,1

1,92

0,88

19

157,7

1,88

0,86

27

156,0

1,87

0,86

 

Величину интервала определим по формуле:

Согласно правилам  округления в качестве ширины интервала возьмем величину 42.

Обозначим границы групп:

1-я группа – 156,0-198,0

2-я группа – 198,0-240,0

3-я группа – 240,0-282,0

4-я группа – 282,0-324,0

После того как определен групировочный признак - капитал, задано число групп - 4 и образованы сами группы, необходимо отобрать показатели, которые характеризуют группы и определить их величины по каждой группе. Показатели, характеризующие банки, разносятся по четырем указанным группам и подсчитываются итоги. Результаты группировки заносятся в таблицу и определяются общие итоги по совокупности по каждому показателю.

Таблица 2.11.

Группировка коммерческих банков по величине капитала

 

Группы банков по величине капитала,

млн. руб.

Число банков

Капитал,

млн. руб.

Активы,

млн. руб.

Рабочие активы,

млн. руб.

А

1

2

3

4

156,0-198,0

198,0-240,0

240,0-282,0

282,0-324,0

17

7

3

3

2965,7

1501,8

730,0

958,8

35,48

17,99

8,74

11,50

16,25

8,25

4,01

5,37

Итого

30

6156,3

73,71

33,88

 

Структурная группировка коммерческих банков на основе данных таблицы 2.11 будет иметь вид:

 

 

Таблица 2.12.

Группировка коммерческих банков по величине капитала

(в %% к итогу)

Группы банков по величине капитала, млн. руб.

Число банков

Капитал

Активы

Рабочие активы

156,0-198,0

198,0-240,0

240,0-282,0

282,0-324,0

48,2

24,4

11,9

15,5

48,1

24,4

11,9

15,6

48,1

24,4

11,9

15,6

48,0

24,3

11,8

15,9

Итого

100,0

100,0

100,0

100,0

 

Из таблицы 3.12 видно, что в основном преобладают малые банки – 48,2%, на долю которых приходится 48,1% всего капитала. Более конкретный анализ взаимосвязи показателей можно сделать на основе аналитической группировки.

Таблица 2.13.

Группировка коммерческих банков по величине капитала

Группы банков по величине капитала,

млн. руб.

Число банков

Капитал,

млн.руб.

Активы,

млн. руб.

Рабочие активы,

млн.руб.

всего

в среднем на

один банк

всего

в среднем на

один банк

всего

в среднем на

один банк

156,0-198,0

17

2965,7

174,5

35,48

2,09

16,25

0,96

198,0-240,0

7

1501,8

214,5

17,99

2,57

8,25

1,18

240,0-282,0

3

730,0

243,3

8,74

2,91

4,01

1,34

282,0-324,0

3

958,8

319,6

11,5

3,83

5,37

1,79

Итого

30

6156,3

205,2

73,71

2,46

33,88

1,13

 

Величина капитала, все активы банка и рабочие активы находятся между собой в прямой зависимости, и чем крупнее банк, тем эффективнее управление работающими активами.

Мы рассмотрели примеры группировок по одному признаку. Однако в ряде случаев для решения поставленных задач такая группировка является недостаточной. В этих случаях переходят к группировке исследуемой совокупности по двум и более существенным признакам во взаимосвязи (комбинационной группировке).

Произведем группировку данных коммерческих банков по двум признакам: величине капитала и работающим активам.

Каждую группу и подгруппу охарактеризуем следующими показателями: число коммерческих банков, капитал, работающие активы.

Таблица 2.14.

Группировка коммерческих банков по величине капитала и работающим активам

Номер группы

Группы банков по величине капитала, млн. руб.

Подгруппы по величине работающих активов, млн. руб.

Число бан-ков

Капи-тал, млн. руб.

Работа-ющие активы, млн. руб.

1

2

3

4

5

6

 

1

156,0-198,0

 

0,86-1,37

1,37-1,88

17

-

2966,5

-

16,25

-

Итого

 

17

2966,5

16,25

2

198,0-240,0

 

0,86-1,37

1,37-1,88

7

-

1501,8

-

8,25

-

Итого

 

7

1501,8

8,25

3

240,0-282,0

 

0,86-1,37

1,37-1,88

3

-

730,0

-

4,01

-

Итого

 

3

730,0

4,01

4

282,0-324,0

 

0,86-1,37

1,37-1,88

-

3

-

958,8

-

5,37

Итого

 

3

958,8

5,37

5

Всего по подгруппам

0,86-1,37

1,37-1,88

27

3

5198,3

958,8

28,51

5,37

Всего

 

30

6157,1

33,88

 

От группировок следует отличать классификацию.

Классификацией называется систематизированное распределение явлений и объектов на определенные группы, классы, разряды на основании их сходства и различия.

Отличительными чертами классификаций является:

·      в их основе лежит качественный признак;

·      классификации стандартны и устанавливаются органами государственной и международной статистики;

·      классификации устойчивы, так как остаются неизменными в течение длительного периода времени.

 

2.4. Ряды распределения

 

Ряды распределения представляют собой простейшую группировку, в которой каждая выделенная группа характеризуется только количеством входящих в нее единиц совокупности.

В рассмотренном нами примере с группировкой банков по величине капитала мы также получили ряд распределения:

таблица 2.15

Распределение коммерческих банков по величине капитала

Капитал банка,

млн. руб.

Количество банков

156,0-198,0

17

198,0-240,0

7

240,0-282,0

3

282,0-324,0

3

Итого

30

 

В зависимости от признака, положенного в основу образования ряда распределения, различают атрибутивные и вариационные ряды распределения.

 

 

 

 

 

 

 

 

 

 


Рис. 2.3.  Виды рядов распределения

Атрибутивными называют ряды распределения, построенные по качественным признакам, то есть признакам, характеризующим состояние изучаемого явления и не имеющим числового выражения.

Атрибутивные ряды распределения характеризуют состав совокупности по тем или иным существенным качественным признакам. Примером атрибутивного ряда распределения может служить распределение экономически активного населения РФ по полу (табл. 4 для раздела 3)

Вариационными рядами называют ряды распределения, построенные по количественному признаку, т.е. признаку, имеющему числовое выражение. Вариационный ряд состоит из двух элементов: вариантов и частот. Вариантами называются отдельные значения признака, которые он принимает в вариационном ряду, то есть конкретное значение варьирующего признака. Частотами называются численности отдельных вариант или каждой группы вариационного ряда. Частоты показывают, как часто встречаются те или иные значения признака в изучаемой совокупности. Сумма всех частот определяет численность всей совокупности, ее объем. Частостями называются частоты, выраженные в долях единицы или в процентах к итогу. Соответственно сумма частостей равна 1 или 100%.

В зависимости от характера вариации признака различают дискретные и интервальные вариационные ряды.

Дискретный вариационный ряд - это ряд распределения в котором группы составлены по признаку, изменяющемуся прерывно, т.е. через определенное число единиц и характеризуют распределение единиц совокупности по дискретному признаку, принимающему только целые значения. Например, группы студентов по баллу в сессию по предмету: 5,4,3,2:

таблица 2.16.

Распределение студентов по баллам в сессию

Балл (оценка)

Количество студентов

5

34

4

37

3

33

2

10

 

Интервальный вариационный ряд распределения – это ряд распределения, в котором группировочный признак, составляющий основание группировки, может принимать в интервале любые значения, отличающиеся друг от друга на сколь угодную малую величину.

Например, распределение работников строительной фирмы по уровню дохода.

Таблица 2.17.

Распределение работников строительной фирмы по уровню дохода

Группы работников, по уровню дохода, тыс.руб.

Число работников,

чел.

Удельный вес,

 % к итогу

До 15,0

60

52,2

15,0-17,5

30

26,1

17,5-210,0

15

13,0

210,0 и более

10

8,7

Итого

115

100,0

 

Построение интервальных вариационных рядов целесообразно прежде всего при непрерывной вариации признака, а также если дискретная вариация признака проявляется в широких пределах, то есть число вариантов дискретного признака достаточно велико.

Правила построения рядов распределения аналогичны правилам построения группировки.

Анализ рядов распределения наглядно можно проводить на основе их графического изображения. Для этой цели строят полигон, гистограмму, кумуляту и огиву распределения.

Полигон используется при изображении дискретных вариационных рядов. Для его построения в прямоугольной системе координат по оси абсцисс (Х) в одинаковом масштабе откладываются значения варьирующего признака, а по оси ординат (Y) наносится шкала для выражения величины частот. Полученные на пересечении оси абсцисс и оси ординат точки соединяются прямыми линиями, в результате чего получают ломаную линию, называемую полигоном частот. Иногда для замыкания полигона предлагается крайние точки (слева и справа на ломаной линии) соединить с точками на оси абсцисс, в результате чего получается многоугольник.

 

 

 

 

 

 

 

 

количество студентов, чел.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

40

 

 

 

 

 

 

 

 

 

 

 

30

 

 

 

 

 

 

 

 

 

 

 

20

 

 

 

 

 

 

 

 

 

 

 

10

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

3

4

5

оценки

 

Рис. 2.4.  Полигон распределения студентов по баллам в сессию

 

 

Гистограмма применяется для изображения интервального вариационного ряда. При построении гистограммы на оси абсцисс откладываются величины интервалов, а частоты изображаются прямоугольниками, построенным на соответствующих интервалах. Высота столбиков должна быть пропорциональна частотам. В результате  получается график, на котором ряд распределения изображен в виде смежных друг с другом столбиков.

 

 

Таблица 2.18.

Ряд распределения консалтинговых фирм

по величине прибыли за 2004 г.

Прибыль, млн. руб.

Количество фирм

20-40

5

40-60

15

60-80

20

80-100

10

 

 

 

 

 

 

 

 

Число фирм

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

20

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

15

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

10

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

5

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

20

40

60

80

100

Прибыль, млн. руб

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Рис. 2.5. Гистограмма и полигон распределения консалтинговых фирм

 по величине прибыли за 2004 год

 

 

Гистограмма может быть преобразована в полигон распределения, если середины верхних сторон прямоугольников соединить прямыми линиями.

При построении гистограммы распределения вариационного ряда с неравными интервалами по оси ординат наносят не частоты, а плотность распределения признака в соответствующих интервалах. Это необходимо сделать для устранения влияния величины интервала на распределение интервала и получения возможности сравнивать частоты. Плотность распределения - это частота, рассчитанная на единицу  ширины интервала, то есть, сколько единиц в каждой группе приходится на единицу величины интервала.

Для графического изображения вариационных рядов может использоваться кумулятивная кривая. При помощи кумуляты  изображается ряд накопленных частот. Накопленные частоты определяются путем последовательного суммирования частот по группам. Накопленные частоты показывают, сколько единиц совокупности имеют значения признака не больше, чем рассматриваемое значение.

При построении кумуляты интервального вариационного ряда по оси абсцисс (х) откладываются варианты ряда, а по оси ординат (у) накопленные частоты, которые наносят на поле графика в виде перпендикуляров к оси абсцисс в верхних границах интервалов. Затем эти перпендикуляры соединяют и получают ломаную линию, то есть кумуляту.

Если при графическом изображении вариационного ряда в виде кумуляты оси х и у поменять местами, то получим огиву.

 

 

 

ТЕМА 3. СТАТИСТИЧЕСКИЕ ПОКАЗАТЕЛИ. АБСОЛЮТНЫЕ И ОТНОСИТЕЛЬНЫЕ ПОКАЗАТЕЛИ

 

3.1. Абсолютные показатели

3.1.1. Абсолютные показатели

Исходной, первичной формой выражения статистических показателей являются показатели в абсолютном выражении или абсолютные величины. Статистические показатели в форме абсолютных величин характеризуют размеры изучаемых статистикой процессов и явлений, а именно, их массу, площадь, объем, протяженность, отражают их временные характеристики, а также могут представлять объем совокупности, т.е. число составляющих ее единиц.

Индивидуальные абсолютные показатели, как правило, получают непосредственно при сборе данных как результат замера, взвешивания, подсчета и оценки интересующего количественного признака, у конкретного объекта: человека, предприятия, домохозяйства и др. В ряде случаев индивидуальные абсолютные показатели имеют разностный характер; например, разность между численностью работников предприятия на конец и на начало года, разность между выручкой от реализации предприятия и общей суммой затрат и т.п.

Сводные абсолютные  показатели, характеризующие общий объем признака или объем совокупности или ее части, получают в результате сводки и группировки индивидуальных значений. К таким показателям относятся общая численность занятых в отрасли, совокупные активы коммерческих банков региона и т.п.

Абсолютные статистические показатели всегда являются именованными числами, то есть они всегда имеют единицы измерения.

В зависимости от социально-экономической сущности исследуемых явлений, их физических свойств они выражаются в натуральных, стоимостных или трудовых единицах измерения.

 

 

Рис. 3.1. Виды единиц измерения абсолютных показателей

 

В международной практике используются такие натуральные единицы измерения как тонны, килограммы, квадратные, кубические и простые метры, мили, километры, галлоны, литры, штуки и т.д. Например, производство электроэнергии в России в 2003 г. составило 915 млрд. кВт×ч, за этот же год добыто 408 млн. т нефти и 620 млрд. куб. м газа.

В группу натуральных также входят условно-натуральные измерители, используемые в тех случаях, когда какой-либо продукт имеет несколько разновидностей и общий объем можно определить только исходя из общего для всех разновидностей потребительского свойства. Так, различные виды органического топлива переводятся в условное топливо с теплотой сгорания 29,3 МДж/кг (7000 ккал/кг), мыло разных сортов - в условное мыло с 40%-ным содержанием жирных кислот, консервы различного объема - в условные консервные банки объемом 353,4 куб.см и т.д.

Перевод в условные единицы измерения осуществляется на основе специальных коэффициентов, рассчитываемых как отношение потребительских свойств отдельных разновидностей продукта к эталонному значению. Так, например, 100 т торфа, теплота сгорания которого - 24 МДж/кг, будут эквивалентны 81,9 т условного топлива (100 * 24,0/29,3), а 100 т нефти при теплоте сгорания 45 МДж/кг будут оцениваться в 153,6 т условного топлива (100 * 45,0/29,3).

В отдельных случаях для характеристики какого-либо явления или процесса одной единицы измерения недостаточно, и используется произведение двух единиц. Примером этому могут служить такие показатели как грузооборот и пассажирооборот, оцениваемые соответственно в тонно-километрах и пассажиро-километрах, производство электроэнергии, измеряемое в киловатт-часах и т.д.

В условиях рыночной экономики наибольшее значение и применение имеют стоимостные единицы измерения, позволяющие получить денежную оценку социально-экономических явлений и процессов. Так, одним из важнейших стоимостных показателей в системе национальных счетов, характеризующим общий уровень развития экономики страны, является валовой внутренний продукт, который в России за 1 квартал 2003 года составил 2893 млрд. рублей.

При анализе и сопоставлении стоимостных показателей необходимо иметь в виду, что в условиях высоких или относительно высоких темпов инфляции они становятся несопоставимыми. Так, сравнивать ВВП России за 2003 год с его величиной, например, за 1993 год вряд ли целесообразно, так как содержание рубля за этот период существенно изменилось. Для того чтобы произвести подобные сравнения там, где это возможно, осуществляют пересчет в сопоставимые цены.

К трудовым единицам измерения, позволяющим учитывать как общие затраты труда на предприятии, так и трудоемкость отдельных операций технологического процесса, относятся человеко-дни и человеко-часы.

Почему важно всегда учитывать единицы измерения показателей?

Потому, что один и тот же показатель может принимать различные количественные выражения в зависимости от выбранных единиц измерения.

Например, партия продукции может характеризоваться следующими величинами:

Ø      1000 штук упаковок или 200 килограмм в натуральном выражении;

Ø      350 тыс. рублей – в стоимостном выражении;

Ø      50 чел.-час. – в трудовых единицах измерения.

Единство или, другими словами, сопоставимость единиц измерения позволяет сравнивать различные объекты, определять соотношения между ними, изучать структуру общественных явлений и процессов по различным показателям.

3.1.2.  Относительные показатели

Относительный показатель представляет собой результат деления одного абсолютного показателя на другой и выражает соотношение между количественными характеристиками социально-экономических процессов и явлений. Без относительных показателей невозможно измерить интенсивность развития изучаемого явления во времени, оценить уровень развития одного явления на фоне других взаимосвязанных с ним явлений, осуществить пространственно-территориальные сравнения, в том числе и на международном уровне.

Относительные показатели получают в результате деления одного абсолютного показателя на другой.

Абсолютный показатель, находящийся в числителе, называется текущим или сравниваемым. Показатель же, с которым производится сравнение и который находится в знаменателе, называется основанием или базой сравнения. Рассчитываемая таким образом относительная величина показывает, во сколько раз сравниваемый абсолютный показатель больше базисного, или какую составляет от него долю, или сколько единиц первого приходится на 1, 100, 1000 и т. д. единиц второго.

Относительные показатели могут выражаться в:

Ø      коэффициентах (долях единицы),

Ø      процентах (%),

Ø      промилле (‰),

Ø      продецимилле (),

Ø      быть именованными числами.

Если база сравнения принимается за 1, то относительный показатель выражается в коэффициентах, если база принимается за 100, 1000 или 10000, то относительный показатель соответственно выражается в процентах (%), промилле () и продецимилле ().

Относительный показатель, полученный в результате соотнесения разноименных абсолютных показателей, в большинстве случаев должен быть именованным. Его наименование представляет собой сочетание наименований сравниваемого и базисного показателей (например, производство какой-либо продукции в соответствующих единицах измерения в расчете на душу населения).

Все используемые на практике относительные статистические показатели можно подразделить на следующие виды:

            1) динамики;

            2) плана;

            3) реализации плана;

            4) структуры;

            5) координации;

            6) интенсивности и уровня экономического развития;

            7) сравнения.

 

Относительный показатель динамики (ОПД).

Как образец характеризует изменение величины показателя во времени. ОПД получают путем деления величины показателя, относящейся к одному временному промежутку (моменту), на величину этого же показателя за другой, как правило, прошедший промежуток или момент времени. Т. е., рассчитывая ОПД, мы сопоставляем величины   одного и того же показателя, взятые за различные временные промежутки.

ОПД представляет собой отношение уровня исследуемого процесса или явления за данный период времени (по состоянию на данный момент времени) к уровню этого же процесса или явления в прошлом:

ОПД =

 

Рассчитанная таким образом величина показывает: во сколько раз текущий уровень превышает предшествующий (базисный) или какую долю от последнего составляет. Данный показатель может быть выражен кратным отношением или переведен в проценты.

Различают относительные показатели динамики с постоянной и переменной базой сравнения. Если сравнение осуществляется с одним и тем же базисным уровнем, например, первым годом рассматриваемого периода, получают относительные показатели динамики с постоянной базой (базисные). При расчете относительных показателей динамики с переменной базой (цепных) сравнение осуществляется с предшествующим уровнем, т.е. основание относительной величины последовательно меняется.

Для примера воспользуемся данными таблицы 3.1.

 

            Таблица 3.1.

Производство легковых автомобилей в РФ в 2000 – 2003гг.
(тыс. шт.)

 

Год

2000

2001

2002

2003

Объем производства

969

1022

981

1011

 

Рассчитаем относительные показатели динамики с переменной и постоянной базой сравнения:

 

           переменная база сравнения     постоянная база сравнения

                   (цепные показатели)           (базисные показатели)

     

                                 

 

                                   

 

                                  

 

Относительные показатели динамики с переменной и постоянной базой сравнения взаимосвязаны между собой следующим образом: произведение всех относительных показателей с переменной базой равно относительному показателю с постоянной базой за исследуемый период. Так, для рассчитанных показателей (предварительно переведя их из процентов в коэффициенты) получим:

 

Относительные показатели плана и реализации плана. Все субъекты финансово-хозяйственной деятельности, от небольших индивидуальных частных предприятий и до крупных корпораций, в той или иной степени осуществляют как оперативное, так и стратегическое планирование, а также сравнивают реально достигнутые результаты с ранее намеченными. Для этой цели используются относительные показатели плана (ОПП) и реализации плана (ОПРП):

 

ОПП =

 

ОПРП =

 

Первый из этих показателей характеризует относительную высоту планового уровня, т.е. во сколько раз намечаемый объемный показатель  превысит достигнутый уровень или сколько процентов от этого уровня составит. Второй показатель отражает фактический объем производства или реализации в процентах или коэффициентах по сравнению с плановым уровнем.

Предположим, оборот торговой фирмы в 2002 г. составил 3,0 млн.руб. Исходя из проведенного анализа складывающихся на рынке тенденций, руководство фирмы считает реальным в следующем году довести оборот до 3,6 млн.руб. В этом случае относительный показатель плана, представляющий собой отношение планируемой величины к фактически достигнутой, составит 120% . Предположим теперь, что фактический оборот фирмы за 2003 г. составил 3,8 млн. руб. Тогда относительный показатель реализации плана, определяемый как отношение фактически достигнутой величины к ранее запланированной, составит 105,6%  .

Между относительными показателями плана, реализации плана и динамики существует следующая взаимосвязь:

ОПП × ОПРП = ОПД

 

В нашем примере:

     или    

 

Основываясь на этой взаимосвязи по любым двум известным величинам при необходимости всегда можно определить третью неизвестную величину.

Относительный показатель структуры (ОПС) представляет собой соотношение структурных частей изучаемого объекта и их целого:

 

ОПС =

 

Выражается относительный показатель структуры в долях единицы или в процентах. Рассчитанные величины, соответственно называемые долями или удельными весами, показывают, какой долей обладает или какой удельный вес имеет та или иная часть в общем итоге.

Рассмотрим структуру валового внутреннего продукта РФ в 1 квартале 2003г. (табл. 3.2.):

Таблица3.2.

Структура валового внутреннего продукта РФ в 1 квартале 2003г.

 

 

Объем

млрд.руб.

% к итогу

ВВП - всего

в том числе:

- производство товаров

- производство услуг

- чистые налоги на продукты

2893

 

917

1635

341

100

 

31,7

56,5

11,8

 

Рассчитанные в последней графе данной таблицы проценты представляют собой относительные показатели структуры (в данном случае - удельные веса). Сумма всех удельных весов всегда должна быть строго равна 100% или 1.

Относительный показатель координации (ОПК) представляет собой отношение одной части совокупности к другой части этой же совокупности:

 

ОПК =

 

При этом в качестве базы сравнения выбирается та часть, которая имеет наибольший удельный вес или является приоритетной с экономической, социальной или какой-либо другой точки зрения. В результате получают, во сколько раз данная часть больше базисной или сколько процентов от нее составляет, или сколько единиц данной структурной части приходится на 1 единицу (иногда - на 100, 1000 и т.д. единиц) базисной структурной части. Так, на основе данных приведенной выше таблицы 5.2 мы можем вычислить, что на каждый рубль произведенных товаров приходится 1,8 руб. произведенных услуг  и 0,4 руб. чистых налогов на продукты .

Относительный показатель интенсивности (ОПИ) характеризует степень распространения изучаемого процесса или явления и представляет собой отношение исследуемого показателя к размеру присущей ему среды:

 

ОПИ =

 

Данный показатель получают сопоставлением уровней двух взаимосвязанных в своем развитии явлений. Поэтому, наиболее часто он представляет собой именованную величину, но может быть выражен и в процентах, промилле, продецимилле.

Обычно относительный показатель интенсивности рассчитывается в тех случаях, когда абсолютная величина оказывается недостаточной для формулировки обоснованных выводов о масштабах явления, его размерах, насыщенности, плотности распространения. Так, например, для определения уровня обеспеченности населения легковыми автомобилями рассчитывается число автомашин, приходящихся на 100 семей, для определения плотности населения рассчитывается число людей, приходящихся на 1 кв.км.

Так, по данным социальной статистики на конец 2003 г. общая численность безработных в РФ составляла 6,1 млн. чел., а экономически активное население – 70,9 млн. чел. Отсюда следует, что уровень безработицы составлял 8,6% .

Разновидностью относительных показателей интенсивности являются относительные показатели уровня экономического развития, характеризующие производство продукции в расчете на душу населения и играющие важную роль в оценке развития экономики государства или региона. Так как объемные показатели производства продукции по своей природе являются интервальными, а показатель численности населения - моментным, в расчетах используют среднюю за период численность населения (предположим, среднегодовую).

Например, рассматривая лишь абсолютный размер ВВП России в 1 квартале 2003 года (2893 млрд. руб.), трудно оценить или "почувствовать" эту величину. Для того, чтобы на основе данной цифры сделать вывод об уровне развития экономики, необходимо сопоставить ее со среднеквартальной численностью населения страны (145,2 млн.чел), которая в простейшем случае рассчитывается как полусумма численности населения на начало и на конец квартала. В результате квартальный размер ВВП на душу населения составит 19,9 тыс. руб.

Относительный показатель сравнения (ОПС) представляет собой соотношение одноименных абсолютных показателей, характеризующих разные объекты (предприятия, фирмы, районы, области, страны и т.п.):

 

ОПС =

 

Для выражения данного показателя могут использоваться как коэффициенты, так и проценты.

Например, согласно официальным статистическим данным, инвестиции в основной капитал  в РФ в 2002 г. за счет средств федерального бюджета составили 81,6 млрд.руб., бюджетов субъектов Федерации и местных бюджетов – 184,5 млрд. руб., средств предприятий – 653,1 млрд.руб. Таким образом можно сделать вывод, что инвестиции за счет средств предприятий в 8 раз превышали инвестиции из средств федерального бюджета и в 3,5 раза превышали  инвестиции из бюджетов субъектов Федерации и местных бюджетов.

3.2. Средние показатели.

 

3.2.1. Сущность и виды средних величин

 

Наиболее распространенной формой статистических показателей, используемой в экономических исследованиях, является средняя величина.

 Средняя величина представляет собой обобщенную количественную характеристику признака в статистической совокупности в конкретных условиях места и времени.

Показатель в форме средней величины выражает типичные черты и дает обобщающую характеристику однотипных явлений по одному из варьирующих признаков. Он отражает уровень этого признака, отнесенный к единице совокупности. Широкое применение средних объясняется тем, что они имеют ряд положительных свойств, делающих их незаменимым инструментом анализа явлений и процессов в экономике.

Важнейшее свойство средней величины заключается в том, что она отражает то общее, что присуще всем единицам исследуемой совокупности. Значения признака отдельных единиц совокупности колеблются в ту или иную сторону под влиянием множества факторов, среди которых могут быть как основные, так и случайные. Например, курс акций корпорации в основном определяется финансовыми результатами ее деятельности. В то же время, в отдельные дни и на отдельных биржах эти акции в силу сложившихся обстоятельств могут продаваться по более высокому или заниженному курсу. Сущность средней в том и заключается, что в ней взаимопогашаются случайные отклонения значений признака, и учитываются изменения, вызванные действием факторов основных. Это позволяет средней отражать типичный уровень признака и абстрагироваться от индивидуальных особенностей, присущих отдельным единицам.

Типичность средней непосредственным образом связана с однородностью статистической совокупности. Средняя величина только тогда будет отражать типичный уровень признака, когда она рассчитана по качественно однородной совокупности. Так, если мы рассчитаем средний курс по акциям всех предприятий, реализуемых в данный день на данной бирже, то получим фиктивную среднюю. Это будет объясняться тем, что используемая для расчета совокупность является крайне неоднородной.  В этом и подобных случаях метод средних используется в сочетании с методом группировок: если совокупность неоднородна - общие средние должны быть заменены или дополнены групповыми средними, т.е. средними, рассчитанными по качественно однородным группам.

Категорию средней можно раскрыть через понятие ее определяющего свойства. Согласно этому понятию средняя, являясь обобщающей характеристикой всей совокупности, должна ориентироваться на определенную величину, связанную со всеми единицами этой совокупности. Эту величину можно представить в виде функции:

f (х1, х2, ..., хn)                                                                    (3.1.)

 

Так как данная величина, в большинстве случаев, отражает реальную экономическую категорию, понятие определяющего свойства средней иногда заменяют понятием определяющего показателя.

Если в приведенной выше функции все величины х1, х2, ..., хn заменить их средней величиной , то значение этой функции должно остаться прежним:

 

f (х1, х2, ..., хn)=                                          (3.2.)

 

Исходя из данного равенства,  и определяется средняя. На практике определить среднюю во многих случаях можно через исходное соотношение средней (ИСС) или ее логическую формулу:

 

 

Так, например, для расчета средней заработной платы работников предприятия необходимо общий фонд заработной платы разделить на число работников:

 

 

Числитель исходного соотношения средней представляет собой определяющий показатель. Для средней заработной платы таким определяющим показателем является фонд заработной платы. Независимо от того, какой первичной информацией мы располагаем - известен ли нам общий фонд заработной платы или заработная плата и численность работников, занятых на отдельных должностях, или какие-либо другие исходные данные - в любом случае среднюю заработную плату можно получить только через данное исходное соотношение средней.

Для каждого показателя, используемого в экономическом анализе, можно составить только одно истинное  исходное соотношение для расчета средней. Если, например, требуется рассчитать средний размер вклада в банке, то исходное соотношение будет следующим:

 

 

Если же необходимо определить среднюю процентную ставку по кредитам, выданным на один и тот же срок, то потребуется следующее исходное соотношение:

 

Однако от того, в каком виде представлены исходные данные для расчета средней, зависит, каким именно образом будет реализовано ее исходное соотношение.

В каждом конкретном случае для реализации исходного соотношения потребуется одна из следующих форм средней величины:

 

·      средняя арифметическая,

·      средняя гармоническая,

·      средняя геометрическая,

·      средняя квадратическая, кубическая и т.д.

 

Перечисленные средние объединяются в общей формуле средней степенной (при различной величине k):

 

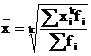                        i=                                              (3.3.)

 

где      х i - i-ый вариант осредняемого признака (i=)

            f i - вес i-го варианта.

 

Помимо степенных средних в экономической практике также используются структурные средние, среди которых наиболее распространены мода и медиана. При осреднении уровней динамических рядов применяются различные виды средней хронологической.

3.2.2. Средняя арифметическая

Наиболее распространенным видом средних величин является средняя арифметическая, которая, как и все средние, в зависимости от характера имеющихся данных может быть простой или взвешенной.

Средняя арифметическая простая. Эта форма средней используется в тех случаях, когда расчет осуществляется по несгруппированным данным.

Предположим, шесть торговых предприятий фирмы имеют следующий объем товарооборота за месяц:

 

Торговое предприятие

1

2

3

4

5

6

Товарооборот (млн.руб.)

 

25

 

18

 

27

 

32

 

15

 

21

 

Для того, чтобы определить средний месячный товарооборот в расчете на одно предприятие, необходимо воспользоваться следующим исходным соотношением:

 

 

Используя приведенные в предыдущем параграфе условные обозначения, запишем формулу данной средней:

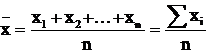                                                      (3.4.)

 

С учетом имеющихся данных получим:

 

млн.руб.

 

В данном случае мы использовали формулу средней арифметической простой (невзвешенной).

Средняя арифметическая взвешенная. При расчете средних величин отдельные значения осредняемого признака могут повторяться, встречаться по несколько раз. В подобных случаях расчет средней производится по сгруппированным данным или вариационным рядам распределения.

Рассмотрим следующий условный пример:

 

Таблица 3.1.

Сделки по акциям эмитента «Х» за торговую сессию

 

Сделка

Количество проданных акций, шт.

Курс продажи, руб.

1

2

3

700

200

950

420

440

410

 

Определим по данному дискретному вариационному ряду средний курс продажи 1 акции, что можно сделать, только используя следующее исходное соотношение:

 

 

Чтобы получить общую сумму сделок необходимо по каждой сделке курс продажи умножить на количество проданных акций и полученные произведения сложить. В конечном итоге мы будем иметь следующий результат:

 

руб.

 

Расчет среднего курса продажи произведен по формуле средней арифметической взвешенной:

 

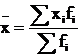                                                              (3.5.)

 

В отдельных случаях веса могут быть представлены не абсолютными величинами, а относительными (в процентах или долях единицы). Так, в приведенном выше примере количество проданных в ходе каждой сделки акций соответственно составляет 37,8% (0,378); 10,8% (0,108) и 51,4% (0,514) от их общего числа. Тогда, с учетом несложного преобразования формулы (6.5.) получим:

 

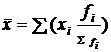                                                       (3.6.)

или

 руб.

 

На практике наиболее часто встречаемая при расчете средних ошибка заключается в игнорировании весов в тех случаях, когда эти веса в действительности необходимы. Предположим, имеются следующие данные:

 

 

 

 

Таблица 3.2.

Себестоимость продукции «Z»

 

Предприятие

Себестоимость единицы продукции, руб.

1

2

37

39

 

Можно ли по имеющимся данным определить среднюю себестоимость данной продукции по двум предприятиям, вместе взятым? Можно, но только в том случае, когда объемы производства данной продукции на двух предприятиях совпадают. Тогда средняя себестоимость составит 38,0 руб. (доказательство этого правила будет приведено ниже.). Однако на первом предприятии за рассматриваемый период может быть произведено, к примеру, 50 единиц продукции, а на втором - 700 единиц. Тогда для расчета средней себестоимости потребуется уже средняя арифметическая взвешенная:

 

 

Общий вывод заключается в следующем: использовать среднюю арифметическую невзвешенную можно только тогда, когда точно установлено отсутствие весов или их равенство.

При расчете средней по интервальному вариационному ряду для выполнения необходимых вычислений от интервалов переходят к их серединам. Рассмотрим следующий пример:

Таблица3.3.

Распределение сотрудников предприятия по возрасту

 

Возраст (лет)

Число сотрудников (чел.)

до 25

25 - 30

30 - 40

40 - 50

50 - 60

60 и более

8

32

68

49

21

3

Итого:

181

 

Для определения среднего возраста персонала найдем середины возрастных интервалов. При этом величины открытых интервалов (первого и последнего) условно приравниваются к величинам интервалов, примыкающих к ним (второго и предпоследнего). С учетом этого середины интервалов будут следующими:

22, 5    27,5     35,0     45,0     55,0     65,0

 

Используя среднюю арифметическую взвешенную, определим средний возраст работников данного предприятия:

 

 года.

 

 

3.2.3. Свойства средней арифметической

 

Средняя арифметическая обладает некоторыми математическими свойствами, более полно раскрывающими ее сущность и в ряде случаев используемыми при ее расчете. Рассмотрим эти свойства:

1.       Произведение средней на сумму частот равно сумме произведений отдельных вариантов на соответствующие им частоты:

 

                                                                   (3.7.)

 

Действительно, если мы обратимся к приведенному выше примеру расчета среднего курса продажи акций (табл. 6.1.), то получим следующее равенство (за счет округления среднего курса правая и левая части равенства в данном случае будут несколько отличаться):

417,03´1850=420´700+440´200+410´950

 

2. Сумма отклонений индивидуальных значений признака от средней арифметической равна нулю:

 

                                                                  (3.8.)

 

Для нашего примера:

(420-417,03)´700+(440-417,03)´200+(410-417,03)´9500

 

Математическое доказательство данного свойства сводится к следующему:

 

 

3. Сумма квадратов отклонений индивидуальных значений признака от средней арифметической меньше, чем сумма квадратов их отклонений от любой другой произвольной величины С:

 

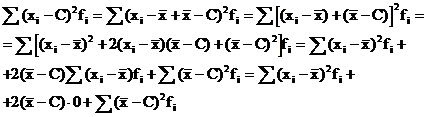           (3.9.)

 

Следовательно, сумма квадратов отклонений индивидуальных значений признака от произвольной величины С больше суммы квадратов их отклонений от своей средней на величину

 

 или

 

На использовании этого свойства базируется расчет центральных моментов, представляющих собой характеристики вариационного ряда при : 1

,

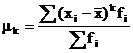где к определяет порядок момента (центральный  момент второго порядка представляет собой дисперсию).

4. Если все осредняемые варианты уменьшить или увеличить на постоянное число А, то средняя арифметическая соответственно уменьшится или увеличится на ту же величину:

 

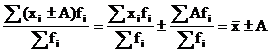                          (3.10.)

 

Так, если все курсы продажи акций увеличить на 15 руб., то средний курс также увеличится на 15 руб.:

 

 руб.

 

5. Если все варианты значений признака уменьшить или увеличить в А раз, то средняя также соответственно увеличится или уменьшится в А раз:

 

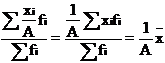                                                     (3.11.)

 

Предположим, курс продажи в каждом случае возрастет в 2 раза. Тогда и средний курс также увеличится на 100%:

 руб.

 

6. Если все веса уменьшить или увеличить в А раз, то средняя арифметическая от этого не изменится:

 

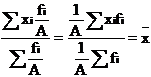                                                        (3.12.)

 

Так, в нашем примере удобнее было бы рассчитывать среднюю, предварительно поделив все веса на 100:

 

 руб.

           

Исходя из данного свойства, можно заключить, что если все веса равны между собой, то расчеты по средней арифметической взвешенной и средней арифметической невзвешенной приведут к одному и тому же результату.

 

3.2.4. Средняя гармоническая

 

Кроме средней  арифметической при расчете статистических показателей могут использоваться и другие виды средних. Однако, в каждом конкретном случае, в зависимости от характера имеющихся данных, существует только одно истинное среднее значение показателя, являющееся следствием реализации его исходного соотношения.

Средняя гармоническая взвешенная используется, когда известен числитель исходного соотношения средней, но неизвестен его знаменатель. Рассмотрим расчет средней урожайности, являющейся одним из основных показателей эффективности производства в агробизнесе:

 

Таблица 3.4.

Валовой сбор и урожайность сельскохозяйственной культуры «Y» по районам области

 

Район

Валовый сбор,

тыс. тонн

Урожайность,

ц/га

А

Б

В

Г

Д

36

53

29

78

20

13

9

15

8

17

 

Средняя урожайность любой сельскохозяйственной культуры в среднем по нескольким территориям, агрофирмам, фермерским хозяйствам и т.п. может быть определена только на основе следующего исходного соотношения:

 

Общий валовой сбор мы получим простым суммированием валового сбора по районам. Данные же о посевной площади отсутствуют, но их можно получить, разделив валовой сбор по каждого района на урожайность. С учетом этого определим искомую среднюю, предварительно переведя для сопоставимости тонны в центнеры:

 

 

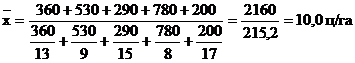
Таким образом, общая посевная площадь данной культуры в целом по области составляла 215,2 тыс.га, а средняя урожайность - 10,0 ц с одного гектара.

В данном случае расчет произведен по формуле средней гармонической взвешенной:

 

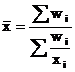, где wi=xifi                                                        (3.13.)

 

Данная формула используется для расчета средних показателей не только в статике, но и в динамике, когда известны индивидуальные значения признака и веса W за ряд временных интервалов.

Средняя гармоническая невзвешенная. Эта форма средней, используемая значительно реже, имеет следующий вид:

 

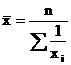                                                                 (3.14.)

 

Для иллюстрации области ее применения воспользуемся упрощенным условным примером. Предположим, в фирме, специализирующейся на торговле по почте на основе предварительных заказов, упаковкой и отправкой товаров занимаются два работника. Первый из них на обработку одного заказа затрачивает 5 мин., второй - 15 мин. Каковы средние затраты времени на 1 заказ, если общая продолжительность рабочего времени у работников равна?

На первый взгляд, ответ на этот вопрос заключается в осреднении индивидуальных значений затрат времени на 1 заказ, т.е. (5+15):2=10, мин. Проверим обоснованность такого подхода на примере одного часа работы. За этот час первый работник обрабатывает 12 заказов (60:5), второй - 4 заказа (60:15), что в сумме составляет 16 заказов. Если же заменить индивидуальные значения их предполагаемым средним значением, то общее число обработанных обоими работниками заказов в данном случае уменьшится:

 

заказов.

 

Подойдем к решению через исходное соотношение средней. Для определения средних затрат времени необходимо общие затраты времени за любой интервал (например, за час) разделить на общее число обработанных за этот интервал двумя работниками заказов:

 

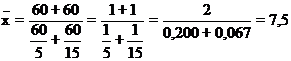 мин.

 

Если теперь мы заменим индивидуальные значения их средней величиной, то общее количество обработанных за час заказов не изменится:

 

 заказов.

 

Подведем итог: средняя гармоническая невзвешенная может использоваться вместо взвешенной в тех случаях, когда значения wi для единиц совокупности равны (в рассмотренном примере рабочий день у сотрудников одинаковый).

 

6.5. Средняя геометрическая и средняя квадратическая

 

Средняя геометрическая. Еще одной формулой, по которой может осуществляться расчет среднего показателя, является средняя геометрическая:

 

                   - невзвешенная                                 (3.15.)

                                                                                                                     

     - взвешенная                         (3.16.)

 

Наиболее широкое применение этот вид средней получил в анализе динамики для определения среднего темпа роста, что будет рассмотрено в соответствующей главе.

Средняя квадратическая. В основе вычислений ряда сводных расчетных показателей лежит средняя квадратическая:

               - невзвешенная                                                                                (3.17.)

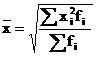           - взвешенная                                                                        (3.18.)

 

Наиболее широко этот вид средней используется при расчете показателей вариации.

В статистическом анализе также применяются степенные средние 3‑го порядка и более высоких порядков.

 

3.2.6. Структурные средние

 

Наиболее часто используемыми в экономической практике структурными средними являются мода и медиана.

Мода представляет собой значение изучаемого признака, повторяющееся с наибольшей частотой.

Медианой называется значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности.

Главное свойство медианы заключается в том, что сумма абсолютных отклонений значений признака от медианы меньше, чем от любой другой величины:

 

                                                                          (3.19.)               

Рассмотрим определение моды и медианы по несгруппированным данным.

Предположим, что 9 торговых фирм города реализуют товар А по следующим оптовым ценам (тыс. руб.).

 

4,4       4,3       4,4       4,5       4,3       4,3       4,6       4,2       4,6

 

Так как чаще всего встречается цена 4,3 тыс.руб., то она и будет модальной.

Для определения медианы необходимо провести ранжирование:

 

4,2       4,3       4,3       4,3       4,4       4,4       4,5       4,6       4,6

 

Центральной в этом ряду является цена 4,4 тыс.руб., следовательно, данная цена и будет медианой. Если ранжированный ряд включает четное число единиц, то медиана определяется как средняя из двух центральных значений.

Если мода отражает типичный, наиболее распространенный вариант значения признака, то медиана практически выполняет функции средней для неоднородной, не подчиняющейся нормальном закону распределения совокупности. Она также используется в тех случаях, когда средняя не позволяет объективно оценить исследуемую совокупность вследствие сильного влияния максимальных и минимальных значений. Проиллюстрируем познавательное значение медианы следующим примером.

Допустим, нам необходимо дать характеристику среднего дохода группы людей, насчитывающей 100 человек, из которых 99 имеют доходы в интервале от 100 до 1000 долл. в месяц, а месячные доходы последнего составляют 50000 долл.:

 

№ п/п    1          2          3          4    ...    50         51   ...    99            100         

 

Доход 100      104      104      107  ...   162       164   ...   200                       50000

(долл.)

 

Если мы воспользуемся средней арифметической, то получим средний доход, равный примерно 600-700 долл., который не только в несколько раз меньше дохода 100-го человека, но и имеет мало общего с доходами остальной части группы. Медиана же, равная в данном случае 163 долл., позволит дать объективную характеристику уровня доходов 99% данной совокупности людей.

Рассмотрим определение моды и медианы по сгруппированным данным (рядам распределения).

Предположим, распределение торговых предприятий города по уровню розничных цен на товар А имеет следующий вид:

 

 

 

Таблица 3.5.

Цена,

руб.

Число торговых предприятий

52

12

53

48

54

56

55

60

56

14

Всего

190

 

Определение моды по дискретному вариационному ряду не составляет большого труда - наибольшую частоту (60 предп.) имеет цена 55 руб., следовательно, она и является модальной.

Для определения медианного значения признака по следующей формуле находят номер медианной единицы ряда:

 

                                                               (3.20.)

где n - объем совокупности.

В нашем случае  .

Полученное дробное значение, всегда имеющее место при четном числе единиц в совокупности, указывает, что точная середина находится между 95 и 96 предприятиями. Необходимо определить, в какой группе находятся предприятия с этими порядковыми номерами. Это можно сделать, рассчитав накопленные частоты. Очевидно, что магазинов с этими номерами нет в первой группе, где всего лишь 12 торговых предприятий, нет их и во второй группе (12+48=60). 95-ое и 96-ое предприятия находятся в третьей группе (12+48+56=116) и, следовательно, медианой является цена 54 руб.

В отличие от дискретных вариационных рядов определение моды и медианы по интервальным рядам требует проведения определенных расчетов на основе следующих формул:

 

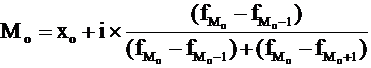             (3.21.)

 

где

Хо   -

нижняя граница модального интервала (модальным называется интервал, имеющий наибольшую частоту);

 

i       -

ширина модального интервала;

 

fМо  -

частота модального интервала;

 

fМо-1 -

частота интервала, предшествующего модальному;

 

fМо+1 -

частота интервала, следующего за модальным.

 

и

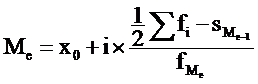                              (3.22.)

 

где

Хо    -

нижняя граница медианного интервала (медианным называется первый интервал, накопленная частота которого превышает половину общей суммы частот);

 

i        -

ширина медианного интервала:

 

Sme-1   -

накопленная частота интервала, предшествующего медианному;

 

fMe        -

частота медианного интервала.

Проиллюстрируем применение этих формул, используя данные таблицы 6.6.

Информация, подобная представленной в этой таблице, необходима для получения четкого представления о покупательной способности населения страны или региона, для оценки эластичности спроса и, в конечном итоге, для выбора того или иного метода ценообразования и обоснования окончательной цены на товар.

 

 

 

Таблица 3.6.

Распределение населения региона по уровню среднедушевого денежного дохода

 

Среднедушевой денежный доход (в среднем за месяц), руб.

Удельный вес населения, %

400 и менее

2,4

400 - 500

15,4

500 - 600

20,1

600 -700

17,2

700 - 800

12,8

800 - 900

9,2

900 - 1000

6,5

1000 - 1100

4,5

1100 - 1200

3,2

1200 - 1300

2,3

свыше 1300

6,4

Всего

100,0

 

Интервал с границами 500 - 600 в данном распределении будет модальным, так как он имеет наибольшую частоту. Использую формулу (6.21), определим моду:

 

 

Для определения медианного интервала необходимо определять накопленную частоту каждого последующего интервала до тех пор, пока она не превысит 1/2 суммы накопленных частот (в нашем случае - 50%):

 

 

Интервал

Накопленная частота, %

 

400 и менее

2,4

 

400 - 500

17,8

 

500 - 600

37,9

 

600 - 700

55,1

 

Мы определили, что медианным является интервал с границами 600 - 700. Определим медиану:

 

 

Соотношение моды, медианы и средней арифметической указывает на характер распределения признака в совокупности, позволяет оценить его асимметрию. Если Мо<Me< - имеет место правосторонняя асимметрия, при <Me< Мо следует сделать вывод о левосторонней асимметрии ряда.

На основе полученных в последнем примере значений структурных средних можно заключить, что наиболее распространенным, типичным является среднедушевой доход порядка 560 руб. в месяц. В то же время, более половины населения располагает доходом свыше 670 руб. при среднем уровне 735 руб. (средняя арифметическая взвешенная). Из соотношения этих показателей следует вывод о правосторонней асимметрии распределения населения по уровню среднедушевых денежных доходов, что позволяет предполагать о достаточной емкости рынка дорогих товаров повышенного качества и товаров престижной группы.

 

 

Занятие 4.

Тема 4.   Основные показатели вариации.

 

Изучив эту тему, Вы будете знать:

·         Что такое показатели вариации и для чего они применяется;

·         Какие показатели относятся к относительным показателям вариации;

·         Какие показатели относятся к абсолютным показателям вариации;

·         Как рассчитываются относительные показатели вариации;

·         Как рассчитываются абсолютные показатели вариации;

·         Какие виды показателей используются для анализа взаимосвязи.

 

Уметь:

·         Рассчитывать как абсолютные так и относительные показатели вариации;

·         Обоснованно выбирать простую или взвешенную форму в зависимости от особенностей  исходной числовой информации;

·         Рассчитывать различные виды дисперсий;

·         Делать обоснованные выводы на основе рассчитанных показателей вариации.

 

При изучении данной темы обратите внимание на следующие понятия и формулы:

·         Дисперсия;

·         Среднее квадратическое отклонение;

·         Коэффициент вариации;

·         Правило сложения дисперсий;

·         Эмпирическое корреляционное соотношение.

 

4.1. Основные показатели вариации

 

Информация о средних уровнях исследуемых показателей обычно бывает недостаточной для полного анализа изучаемого процесса или явления.  Иногда совершенно непохожие по своему внутреннему строению совокупности могут иметь равные средние величины. Поэтому для более детального изучения того или иного явления необходимо учитывать разброс или вариацию значений отдельных единиц совокупности. Измерение вариации признаков имеет как теоретическое, так  и практическое значение.                               

Так,   например, для выявления наиболее стабильно работающего коллектива   или предприятия наравне с другими показателями рассчитывают и основные показатели вариации. Эти показатели  дают возможность количественно определить размеры устойчивости  производительности труда, уровня квалификации, цен на основные виды выпускаемой продукции и т.п. Измерение размеров вариации такого показателя как « выполнение  работ в срок» имеет важное значение для принятия решений  заказчиками и инвесторами, т.к. ситуация, в которой присутствует изменчивость признака, часто содержит риск. Особое значение показатели вариации приобретают в анализе рынка ценных бумаг, где мера колеблемости отождествляется с мерой рискованности вложения денежных средств.

Основными показателями, характеризующими вариацию, являются :

- размах,

- дисперсия,

- среднее квадратическое отклонение,

- коэффициент вариации.

Для иллюстрации расчетов этих показателей воспользуемся следующими данными:

 

                 Таблица.4.1.

Имеются  данные о продаже основных марок холодильников:

Модель

Цена ($)

Объем продаж (шт.)

Siemens

1000

30

Bosch

800

26

AEG Santo

900

24

Miele KF

1200

30

Gorenje

870

20

Haier

570

23

Samsung

760

30

Zanussi

700

20

Daewoo

460

20

Beko

650

25

Candy

480

20

Whirpool

470

21

 

Простейшим показателем, уже использованным выше при группировке данных, является  размах вариации. Он представляет собой разность максимального и минимального значений признака:

R =  X max   -  X min

R =  1200 – 460 = 740 $

Этот показатель служит незаменимой мерой разброса экстремальных значений признака. Кроме характеристики границ разброса признака, размах вариации может быть использован  для выявления ошибок.  При наличии очень больших (или очень малых)  ошибочно записанных значений признака размах вариации сразу резко возрастает, что требует проверки и корректировки исходных данных.

Недостатком данного показателя является то, что он оценивает только границы варьирующего признака и не отражает его колеблемость внутри этих границ. Вследствие этого размах вариации может неправильно характеризовать  общую колеблемость  признака.

Этого недостатка лишен другой показатель - дисперсия, рассчитываемый как средний квадрат отклонений значений признака от их средней величины. Между индивидуальными отклонениями от средней и колеблемостью признака существует прямая зависимость: чем сильнее колеблемость признака, тем больше отклонения  его значений от средней величины и менее устойчив изучаемый показатель.

 Как и средняя величина этот показатель может быть рассчитан в двух формах: взвешенной и невзвешенной:

            невзвешенная форма

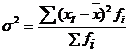        взвешенная форма

где    - отдельные значения признака

 - общая средняя

 -  вес варианта признака в общей совокупности.

По приведенным выше данным определим средневзвешенную цену холодильника и рассчитаем дисперсию:

Дисперсию в отдельных случаях  удобнее рассчитывать по другой формуле:

, т.е. дисперсия равна разности средней из квадратов индивидуальных значений признака и  квадратом средней  величины.

Эту формулу можно представить иначе:

- невзвешенная форма

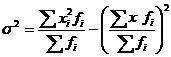-  взвешенная форма

Следует отметить, что дисперсия еще не дает представления об однородности совокупности, и этому показателю трудно дать экономическую интерпретацию, т.к он рассчитан в квадратных единицах. Поэтому следующим шагом в исследовании однородности совокупности является расчет среднего квадратического отклонения, показывающего на сколько в среднем отклоняются конкретные варианты признака от его среднего значения. Оно определяется как квадратный корень из дисперсии и имеет ту же размерность  что и изучаемый признак:

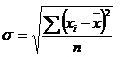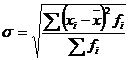 - невзвешенная форма

   -  взвешенная форма

В нашем примере среднее квадратическое отклонение равно:

Таким образом, цена каждой марки холодильника отклоняется от средней цены  в среднем на 271,1$ .

Рассмотренные показатели позволяют получить абсолютное значение вариации признака. Однако для сравнения разных совокупностей с точки зрения устойчивости какого-либо одного признака или для определения однородности совокупности рассчитывают относительные показатели.

Эти показатели вычисляются как отношение размаха вариации,  среднего линейного отклонения или среднего  квадратического отклонения  к средней арифметической или медиане.  Чаще всего эти показатели  выражаются в процентах.

Коэффициент осцилляции ():

=

Линейный коэффициент вариации  ():

=

Наиболее распространенным показателем является коэффициент вариации :

Определим значение этого показателя по данным таблицы 1:

Рассчитанная величина свидетельствует о неоднородности цен на холодильники, т.к. однородной совокупность считается, если коэффициент вариации меньше 33% (для распределений близких к нормальному).

Следует отметить, что коэффициент вариации может быть более 100%, что, в частности, может быть при  наличии  значений сильно отличающихся от средней величины.  Такой результат означает, что в исследуемой совокупности сильна вариация признаков по отношению к средней величине.

Если исследуется вариация альтернативных признаков, т.е.признаков, которыми одни единицы совокупности  обладают, а другие – нет, то дисперсия альтернативного признака определяется по формуле :

 , где

p – доля единиц, обладающих данным признаком,

q – доля единиц не обладающих данным признаком.

 

Максимальное значение дисперсии доли равно 0,25 ( когда p=q=0,5).

Информативность показателей вариации повышается, если они рассчитываются для целей сравнительного анализа. При этом показатели рассчитанные по одной совокупности сопоставляются с показателями, рассчитанными по другой аналогичной совокупности или по той же самой , но относящейся к другому периоду времени. Например, исследуется динамика вариации  на товары длительного пользования по месячным или ежегодным данным в одном и том же торговом предприятии или за один и тот же период времени , но по разным регионам.

 

4.2. Использование показателей вариации в анализе взаимосвязей.

 

Изучая вариацию интересующего нас признака в пределах исследуемой совокупности и опираясь на общую среднюю в расчетах, трудно оценить степень воздействия на него какого-либо отдельного   признака.

При проведении такого анализа исходная совокупность должна представлять собой  множество единиц, каждая из которых характеризуется двумя признаками – факторным ( оказывающим влияние на взаимосвязанный с ним признак) и результативным (подверженным  влиянию).

Для выявления взаимосвязи исходная совокупность делится по факторному признаку на группы. Выводы о степени взаимосвязи базируются на анализе вариации результативного  признака. Если статистическая совокупность разбита на группы по какому-либо признаку, то для оценки влияния различных факторов, определяющих вариацию индивидуальных значений признака,  используют  правило сложения дисперсий.

Общая дисперсия  представляет собой сумму средней из внутригрупповой  и межгрупповой и дисперсий:

,

где

  - общая дисперсия

 -    средняя из внутригрупповых дисперсий

-    межгрупповая дисперсия

Общая дисперсия характеризует вариацию признака по всей совокупности  как результат влияния всех факторов, определяющих индивидуальные различия единиц совокупности.

 ,

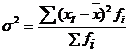где   - отдельные значения признака

             - общая средняя варьирующего признака

             -  вес варианта признака в общей совокупности.           

Межгрупповая дисперсия характеризует вариацию, обусловленную влиянием фактора, положенного в основу группировки.

,

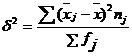где - общая средняя варьирующего признака

       - средняя j- ой группы

       - число единиц в j-ой группе  ()

Средняя из внутригрупповых дисперсий отражает ту часть вариации результативного признака ,  которая обусловлена действием  всех прочих неучтенных факторов, кроме фактора, по которому осуществлялась группировка . Другими словами внутригрупповая дисперсия отражает случайную вариацию. Внутригрупповая дисперсия рассчитывается отдельно по каждой  j-ой группе.

,

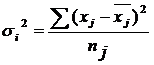где - значение признака у отдельных элементов j-ой группы

        -       средняя j-ой группы

      -        число единиц j-ой группы

Для всех групп в целом вычисляется средняя из внутригрупповых дисперсий, взвешенных на частоты соответствующих групп по формуле:

=

Взаимосвязь между тремя видами дисперсий получила название  правила сложения дисперсий. Таким образом, зная два вида дисперсий всегда можно определить третий:   . Из этого равенства следует, что общая дисперсия, как правило, будет больше средней из групповых дисперсий.  Это обусловлено тем, что при расчленении общей совокупности единиц на части по какому-либо признаку образуются более или менее однородные группы, в результате чего сокращается колеблемость признаков в пределах каждой группы. Это приводит к тому, что средняя из групповых дисперсий оказывается меньше дисперсии признака по всей совокупности единиц, причем разница между этими показателями будет тем больше, чем однороднее получаются группы в результате расчленения общей совокупности.

Теснота связи между факторным и результативным признаками оценивается на основе эмпирического корреляционного отношения:

Данный показатель может принимать значения от 0 до 1. Чем ближе к 1 будет его величина, тем сильнее взаимосвязь между рассматриваемыми признаками.

На следующем условном примере исследуем зависимость объема выполненных работ от формы собственности проектно-изыскательских организаций.

Таблица 4.2.

 

Выполнение работ проектно-изыскательскими организациями разной формы собственности

 

Форма собственности

Количество предприятий

Объем выполненных работ (млн.р.)

Итого

Государственная

4

10, 30, 20, 40

100

Негосударственная

6

20, 40, 60, 20, 50, 50

240

Итого:

10

 

340

 

Решение:

1. Определяется средний объем выполненных работ для предприятий двух форм собственности.

млн.р.

2. Определяется средний объем выполненных работ для каждой формы собственности.

млн.р.

млн.р.

и3. Рассчитывается общая и внутригрупповые (т.е. для каждой группы) дисперсии.

 

4. Определяется средняя из внутригрупповых и межгрупповая дисперсия. Для этого расчета полученные ранее данные заносятся в таблицу.

Таблица 4.3.

Вспомогательная таблица

 

Форма собственности

Число предприятий

Средняя по группе

Внутригрупповые дисперсии

Государственная

4

25

125

Негосударственная

6

40

233

Итого

10

 

 

 

Средняя из внутригрупповых дисперсий

Межгрупповая дисперсия

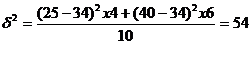
На последнем этапе решения задачи необходимо проверить тождество, отражающее закон сложения дисперсий:

54,0+189,8=243,8

Таким образом, можно сделать вывод о том, что объем работ, выполненных проектно-изыскательскими организациями на 22% [(54,0/243,8)х100%] зависит от фактора, положенного в основание группировки, т.е. от формы собственности., а на 78% [(189,8/243,8)х100%)] – от прочих факторов.

Вывод о том, что объем выполненных работ  в гораздо большей степени зависит от каких-либо других факторов, чем от формы собственности предприятий подтверждается и величиной эмпирического корреляционного отношения:

Величина этого показателя свидетельствует о том, что зависимость объема работ от формы собственности предприятия невелика.

 


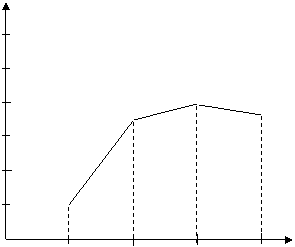
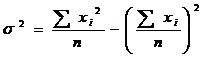1 При С=0 получают начальные моменты (начальный момент 1-го порядка - средняя арифметическая и т.д.).