Дисциплина «Имитационное моделирование экономических процессов» разработана на основе учебной программы дисциплины «Имитационное моделирование экономических процессов» МФПУ «Синергия» с учетом государственного образовательного стандарта по специальности «Прикладная информатика в экономике», утвержденного Министерством образования и науки Российской Федерации, и предназначена для студентов факультета Информационных систем и технологий МФПУ «Синергия».

Дисциплина входит в состав цикла специальных дисциплин. Она посвящена изучению основных понятий, методов и инструментальных средств имитационного моделирования и их применению к решению задач анализа и проектирования экономических процессов. Дисциплина формирует общую систему теоретических и концептуальных представлений о методологической основе теории, а также развивает ряд практических навыков и умений, позволяющих студентам впоследствии применять полученные знания и навыки для решения прикладных задач в своей области деятельности.

Целью изучения дисциплины является углубленное изучение возможностей имитационного моделирования применительно к процессам управления и организации работы предприятий, подготовка студентов к профессиональной деятельности в сфере управления в организациях различного профиля и форм собственности.

Задачи спецкурса:

· раскрытие сущности и содержания основных понятий и определений методологии имитационного моделирования;

· ознакомление с основными возможностями и практическими приложениями методологии;

· изучение основных методов и технологий создания моделей;

· формирование навыков самостоятельной работы студентов по решению типичных задач в области постановки задачи моделирования и планирования имитационных экспериментов.

В результате изучения дисциплины студенты должны:

Знать:

· классификацию моделей, основные этапы жизненного цикла имитационного моделирования, алгоритмы, применяемые для компьютерной имитации процессов, возможности современных систем имитации, методы рациональной организации и планирования имитационных экспериментов.

Уметь:

· правильно формулировать задачу анализа и оценивания параметров деловых процессов, определять стратегические цели имитационных экспериментов, проводить рациональный выбор моделей, выбирать и применять методы организации имитационных прогонов и статистической обработки получаемых результатов.

Иметь представление:

· об основных методах имитации динамики процессов, действия случайных факторов, существующих программных средствах создания и применения имитационных моделей, типовых правилах и приемах создания моделей в современных моделирующих комплексах.

Тема 1. Имитационное моделирование в анализе и управлении экономическими процессами

Цели изучения темы:

· выяснить предмет изучения;

· понять значение изучаемой методологии для решения задач управления экономическим объектом.

Задачи изучения темы:

· очертить смысл применяемых понятий;

· специфицировать возможности и области применения имитационных моделей.

Успешно изучив тему, Вы:

Получите представление о:

· специфике экономических процессов;

· основных подходах к решению задач анализа экономических процессов;

· возможностях методологии имитационного моделирования.

Будете знать:

· основные возможности имитационного моделирования;

· особенности задач, связанных с экономическими процессами;

· преимуществах имитационного моделирования в сравнении подходом на основе экспериментов с реальной системой.

Вопросы темы:

1. Экономические процессы.

2. Имитационное моделирование как метод анализа и синтеза экономических процессов.

3. Имитационное моделирование как инструмент управления.

Вопрос 1. Экономические процессы.

Рассматриваемый в настоящем курсе подход с успехом может применяться к задачам, которые возникают при анализе и проектировании процессов, протекающих в управленческих и общественных образованиях. Это соображение явилось (дополнительно к прочим) причиной того, что в дальнейшем изложении для обозначения характера изучаемых процессов часто будет использоваться термин деловой процесс. Близкий по значению термин бизнес-процесс, представляющий собой транслитерацию английского названия, семантически ограничен, поскольку, строго говоря, относится только к деятельности по своему характеру коммерческой (см. словарь Merriam -Webster). Разумеется, экономический процесс, если понимать под этим термином процесс, который протекает внутри какого-либо объекта экономики, охватывается понятием деловой процесс. К деловому процессу мы будем относить любой вид регулярно выполняющихся действий или операций, направленных на достижение одной или нескольких определенных целей и имеющих (или использующих) необходимый для этого набор ресурсов.

Основные задачи, которые приходится решать руководителям предприятия и аналитикам, состоят в том, чтобы, во-первых, понять текущее состояние, и, во-вторых, определить пути для улучшения и инноваций. Под улучшением деловых процессов понимаются их небольшие поэтапные изменения, носящие непрерывный эволюционный характер. Инновации означают существенные изменения, носящие дискретный характер. Дающие потенциальную возможность значительно повысить эффективность деловых процессов инновации вместе с тем характеризуются высоким уровнем риска неудачи.

Наиболее радикальным видом инноваций является реинжиниринг деловых процессов, применение которого может, с одной стороны, повысить эффективность в несколько раз, с другой стороны, увеличивает риск.

Деловым процессам присущ ряд особенностей, что затрудняет решение связанных с ними задач. Можно, в частности, отметить следующие факторы.

· сотрудники являются участниками сразу нескольких деловых процессов;

· производительность сотрудников в разные временные периоды может различаться;

· выполнение отдельных заданий (задач) характерно тенденцией к накоплению заданий с последующим выполнением непрерывно во времени всей накопленной совокупности;

· сам процесс может в зависимости от складывающихся условий подвергаться изменениям и протекать по-разному.

Вопрос 2. Имитационное моделирование как метод анализа и синтеза экономических процессов.

Инновационная деятельность и реинжиниринг деловых процессов требуют проведения тщательного анализа, для которого могут применяться различные средства. Для анализа и проектирования деловых процессов можно прибегнуть либо к эксперименту на реальной системе, либо к предварительной проверке на имитационной модели. Цель проведения имитационного моделирования может заключаться как в получении новых знаний относительно моделируемой системы, так и в ее улучшении.

Имитационное моделирование сводится к воспроизведению с помощью компьютера реальных процессов в их развитии во времени. Деятельность предприятия или других объектов имитируется в компьютере пошаговым перемещением за сжатое время от события к событию, с отображением при необходимости анимированной картины реального процесса.

Программные средства имитационного моделирования отслеживают все изменения статистических данных о работе элементов модели, которые затем выводятся как итоговые результаты моделирования и могут анализироваться и оцениваться.

Входные параметры модели можно менять, в частности, с тем, чтобы проанализировать, как изменение ресурсов влияют на сроки и прочие показатели процесса доставки, можно проводить варьирование значений, определяющих потребности в ресурсах, которые необходимы для удовлетворения заказов клиентов.

Применяя подход на основе имитационного моделирования к анализу экономических процессов можно решать следующие важные задачи:

1. Получать количественные оценки:

· временных характеристик;

· стоимостных показателей;

· величины необходимых ресурсов;

· производительности системы;

· производственных мощностей;

· узких мест.

2. Получать визуальное представление и осуществлять проверки:

· протекающих процессов;

· проблемных областей и участков;

· «снимков» состояния системы;

· организационных связей и взаимодействий элементов.

3. Планировать усовершенствования и проводить их предварительную проверку в части:

· распределения ресурсов;

· оптимизации потоков;

· упрощения технологии.

4. Разрабатывать методы улучшения:

· производительности;

· финансовых показателей;

· экономической отдачи инвестиций.

5. Наилучшим образом организовать взаимодействие:

· владельцев деловых процессов;

· лиц, принимающих решения;

· исполнителей и участников процесса.

По отношению к эксперименту на реально существующей системе имитационное моделирование характеризуется следующими преимуществами:

1. Уменьшение стоимости.

Проведение экспериментов с реальной системой может потребовать больших финансовых затрат и часто связано с нарушением нормального режима или даже приостановкой функционирования системы.

В противоположность этому имитационные эксперименты не мешают нормальной работе исследуемой системы, а выяснение последствий каких-либо планируемых изменений в ее структуре и параметрах легко осуществить внесением изменений в модель с последующими имитационными экспериментами на этой модели.

2. Сокращение времени исследований.

Проведение экспериментов с реальной системой может потребовать больших временных затрат и может в зависимости от ее типа занять недели и месяцы до того, как будут собраны все необходимые результаты.

В противоположность этому имитационные эксперименты занимают минуты или (реже) часы, что может оказаться принципиально важным, поскольку полученные результаты могут с течением времени быстро обесцениваться.

3. Возможность управления условиями эксперимента.

Рамки экспериментов с реальной системой в значительной степени ограничены отсутствием возможности изменять условия эксперимента. Например, большой интерес представляет поведение цепочки поставок в условиях каких-либо сбоев или нарушений нормальной работы. Однако исследование функционирования реальной системы провести будет затруднительно в силу того, что эти события случаются довольно редко.

В противоположность этому имитационные эксперименты могут проводиться на произвольно задаваемых наборах входных данных, которые могут повторяться неограниченное число раз.

4. Исключение проблемы доступности реальной системы.

Проведение экспериментов с реальной системой может оказаться принципиально невозможным в тех случаях, когда система еще не создана и целесообразность ее создания необходимо оценить, или когда требуется найти (проверить) какие-либо проектные решения после того, как решение о создании уже принято.

Применение имитационной модели оказывается в этих случаях единственной возможностью.

По отношению к моделям, построенных на других принципах, имитационное моделирование обладает следующими преимуществами:

1. Учет случайных факторов.

Моделируемые системы подвержены воздействия возмущающих параметров, которые наряду со многими внутренними параметрами, носят случайный характер. Аналитические модели, в частности, модели теории массового обслуживания, строятся на некоторых допущениях относительно законов распределения случайных величин, описывающих эти воздействия и параметры, применяемых дисциплин обслуживания и имеют ряд других ограничений. Поэтому области применения этих моделей обусловлены действием этих ограничений, а точность результатов, получаемых на их основе, часто оказывается недостаточной для решения практических задач.

В имитационной модели можно учесть случайный характер воздействия возмущающих параметров или внутренних параметров моделируемой системы сколь угодно близко к их реальным характеристикам.

2. Прозрачность модели.

Достоинством имитационной модели является ее возможность проследить внутренние механизмы происходящих явлений и получать в виде анимации на дисплее наглядную картину протекающих в реальной системе процессов.

Вместе с тем, применение подхода на основе имитационного моделирования в некоторых случаях может оказаться по ряду причин нецелесообразным. Отметим наиболее существенные из этих причин:

1. Высокая стоимость.

Больших затрат могут потребовать:

· моделирующие программные системы (комплексы), на основе которых создаются имитационные модели;

· работа по созданию имитационной модели, в которой участвуют как специалисты-аналитики, занятые разработкой модели, так и специалисты-прикладники, привлекаемые для консультирования;

· планирование, проведение и обработка результатов имитационных экспериментов.

2. Длительное время.

Продолжительное время может потребоваться как для создания модели, так и для проведения на ее основе необходимых экспериментов.

3. Большие объемы исходных данных.

Построение модели и проведение экспериментов требуют исходных данных, объем которых часто бывает весьма значительным. Сбор и подготовка данных представляют собой отдельную задачу, которая может вылиться в существенные затраты на ее решение.

4. Высокие квалификационные требования.

Создание модели требует применения усилий специалистов, обладающих хорошими знаниями и опытом практической работы в целой совокупности дисциплин, таких как системный анализ, высшая математика, теория вероятностей, математическая статистика и программирование, которые должны дополняться организаторскими способностями и умением осуществлять управление проектами. Специалистов, обладающих всеми необходимыми знаниями и умениями, не всегда бывает просто найти.

5. Риск переоценки результатов.

Довольно часто встречается излишне завышенная оценка значимости результатов, получаемых с помощью компьютерных программ, хотя эти результаты подчас нельзя считать в достаточной степени обоснованными и точными. Кроме того, получаемые в итоге имитационных экспериментов выходные данные нуждаются в правильной их интерпретации, что также происходит далеко не всегда.

Таким образом, выбор метода исследования в пользу имитационной модели должен делаться не во всех, а только в обоснованных случаях. Когда для решения задачи существует аналитическая модель, обеспечивающая получение результата с приемлемой точностью, ее применение в большинстве случаев будет более оправданным: стоимостные затраты на создание модели либо значительно меньше, либо вовсе отсутствуют (если используется уже готовая модель), а временные затраты на получение результатов (т.е., на выполнение математических расчетов) незначительны.

Дать полный перечень областей, в которых подход может применяться, практически невозможно. Укажем только некоторые из наиболее часто встречающихся в публикациях:

· производственные процессы и предприятия;

· транспортные предприятия и перевозочные процессы;

· строительство и строительные компании;

· информационно-коммуникационные системы;

· логистические процессы;

· медицинское обслуживание;

· военное дело.

Вопрос 3. Имитационное моделирование как инструмент управления.

Имитационное моделирование является инструментом управления изменениями. Практики в управлении деловыми процессами знают исключительную важность для процесса преобразований структуры предприятия и применяемой технологии к более совершенным формам ведения дел, и имитационное моделирование является одним из способов ускорить реализацию изменений. Эта возможность в значительной степени обусловлена способностью имитационного моделирования объяснять причины наблюдаемых изменений. Имитационное моделирование дает нечто большее, чем просто ответ на поставленный вопрос: оно показывает, каким образом ответ был получен, и позволяет выявить причины, которые приводят к определенному эффекту и дать объяснения предлагаемым решениям.

Эти возможности являются причиной того, что имитационные модели могут применяться не только как метод анализа реальных процессов, но и как средство, непосредственно включаемое в контур управления объекта. Несмотря на то, что включение модели приводит к дополнительным расходам и необходимости создания инфраструктуры для функционирования модели, обойтись без них в реальной обстановке (в режиме реального времени, управляемой событиями) невозможно. На Рис. 1 показаны механизмы взаимодействия модели физической системы и модели управления этой системой в процессе совместной работы в реальном времени.

Рис. 1. Взаимодействие модели физической системы и модели управления

Прогоны модели системы выполняются параллельно с работой изучаемой (моделируемой) системы. Фактические значения параметров и их значения, полученные на модели, сравниваются и подвергаются анализу в модели управления, с помощью которой определяется последовательность шагов, которые необходимо выполнить для того, чтобы привести значения параметров системы к желаемым. Широкие стрелки означают, что в системе могут быть реализованы как автоматизированный, так и ручной режимы.

Получая все большее развитие, средства имитационного моделирования процессов начинают входить в состав делового инструментария в качестве компонентов, интегрированных в систему анализа и организации деловых процессов. Это проявляется в том, что:

· Программное обеспечение для поддержки имитационного моделирования все чаще встраивается непосредственно в среду, реализующую деловые процессы.

· Информация, являющаяся результатом имитационного моделирования, и данные, характеризующие функционирование процесса, формируют потоки взаимообмена между компонентом моделирования и прочими компонентами деловой системы.

· Для руководителей выполнением операций применение имитационного моделирования позволяет прогнозировать результаты протекания тех или иных деловых процессов без дополнительной рабочей нагрузки.

· Возможность статического инструменты моделирования (например, электронные таблицы) весьма ограничены и позволяют, в частности, проводить оптимизацию структуры и параметров сложных процессов. Для решения сложных задач требуются такие инструменты, как имитационное моделирование, которое позволяет учитывать нелинейные взаимозависимости.

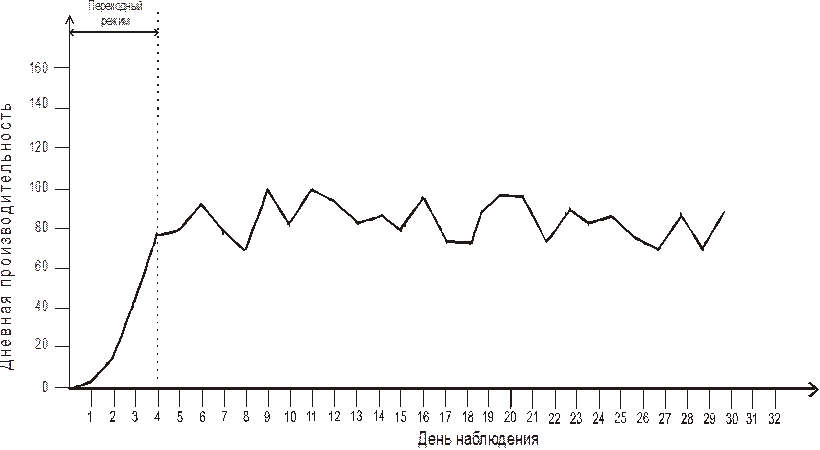
В результате за счет использования «живых» данных и статистических распределений достигается существенное улучшение результатов анализа. На Рис. 2 показан пример (K.Jones, C .McCarty Trends in Modern Business Process Simulation Tools http://simprocess.com/pdf/2194_Jones.pdf) результатов имитационного прогона модели процессов работы с персоналом.

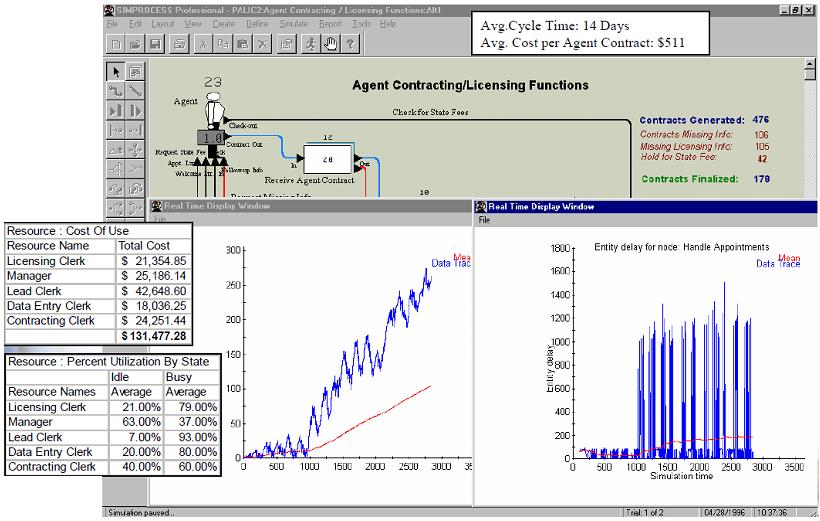
Рис. 2. Пример результатов имитационного прогона

Приведем примеры только некоторых из сфер деятельности крупной компании или предприятия, в которых с успехом применяется имитационное моделирование.

Оказание услуг.

Имитационное моделирование может помочь в проектировании реалистичных процедур обслуживания клиентов, определении параметров процедур и степени удовлетворенности клиентов качеством обслуживания.

Реакция на отклонения.

При возникновении каких-либо нарушений нормального протекания деловых процессов имитационное моделирование может помочь в проведении анализа возникшей ситуации и определении обходных путей и методов выхода из этой ситуации, а также в проведении планирования необходимых действий.

Управление запасами и доступом к ресурсам.

Используя имитационное моделирование можно определять, обеспечен ли в настоящий момент деловой процесс достаточными ресурсами и есть ли к ним практический доступ, а также прогнозировать состояние с обеспеченностью и доступностью в будущем.

Доставка и дистрибуция.

Имитационное моделирование может способствовать выявлению альтернативных подходов для доставки, которые обеспечат соблюдение требований по срокам, и провести предварительную проверку соблюдения требований и анализ всех показателей работы служб доставки и дистрибуции.

Выводы:

1. Основными задачами, стоящими перед руководством различного уровня, являются задачи совершенствования структуры и параметров деловых процессов. К наиболее радикальным из этих задач относятся инновационная деятельность и реинжиниринг, для решения которых могут применяться как эксперименты на реальной системе, так и подход на основе моделирования, который в большинстве случаев предпочтительнее.

2. Наиболее универсальным и эффективным видом моделирования является имитационное моделирование, которое обладает рядом преимуществ как по отношению к эксперименту на реальной системе, так и по отношению к другим видам моделей.

3. Уникальной возможностью имитационных моделей является то, что они могут применяться не только в качестве средства анализа реальных процессов, но и как элемент управления объектом, в частности, экономическим.

Вопросы для самопроверки:

1. Что такое деловой процесс?

2. Как формулируются основные задачи, относящиеся к анализу и проектированию деловых процессов?

3. Что такое реинжиниринг?

4. Какие можно отметить особенности, присущие деловым процессам?

5. Какие основные подходы используются для анализа и проектирования деловых процессов?

6. Как можно кратко пояснить сущность имитационного моделирования?

7. Какие основные задачи анализа деловых процессов можно решать с помощью имитационного моделирования?

8. В чем состоят преимущества подхода на основе имитационного моделирования по отношению к экспериментированию на реально существующей системе?

9. В чем состоят преимущества подхода на основе имитационного моделирования по отношению к моделированию, основанному на других принципах?

10. В каких случаях применение имитационного моделирования может быть нецелесообразным?

11. Какие из прикладных областей, где применение имитационного моделирования наиболее эффективно, можно отметить?

12. Какую важную помощь аналитику помимо получения количественных оценок показателей процессов может оказать имитационная модель?

13. В каких целях может применяться имитационная модель помимо целей анализа реальных процессов?

14. В каких формах могут реализовываться имитационные модели?

15. Приведете примеры видов деятельности предприятия, где могут использоваться имитационные модели?

Литература по теме:

Основная литература:

1. Емельянов А. А. Имитационное моделирование экономических процессов/ А. А. Емельянов, Е.А.Власова, Р.В.Дума.– М.: Финансы и статистика, 2009 – 416 с.

Дополнительная литература:

1. Jones K., McCarty C. Trends in Modern Business Process Simulation Tools. – SEPG North America, 2009. – http://simprocess.com/pdf/2194_Jones.pdf

2. Коблев Н. Основы имитационного моделирования сложных экономических систем. – М.: Дело, 2003. – 336 с.

3. Н.Н. Снетков Имитационное моделирование экономических процессов. Учебно-практическое пособие – М.: Изд. центр ЕАОИ, 2008. – 228 с.

4. Советов Б.Я., Яковлев С.А. Моделирование систем. – М.: Высшая школа, 2003 – 320 с.

Практические задания:

1. Выберете в качестве примера какой-либо из объектов, с которым приходится сталкиваться в повседневной жизни (бензоколонка, сервисный центр, отделение банка, районная поликлиника, рекрутинговая компания) и попробуйте дать ответы на следующие вопросы.

а) Какие деловые процессы этого объекта можно выделить?

б) Какие возможные улучшения следовало бы рассмотреть?

в) Как могло бы помочь имитационное моделирование для поиска направлений улучшений и оценивания их степени?

Тема 2. Методологические основы имитационного моделирования

Цели изучения темы:

· изучить основные подходы к построению имитационных моделей.

Задачи изучения темы:

· определить основные методологические принципы реализации имитационных моделей;

· узнать возможные классификации моделей;

· познакомиться с методом Монте-Карло;

· выяснить, как организуется процесс создания и применения имитационных моделей.

Успешно изучив тему, Вы:

Получите представление о:

· сущности подхода на основе системной динамики;

· сущности подхода на основе дискретно событийного моделирования;

· характерных особенностях моделей различных типов.

Будете знать:

· как классифицируются модели;

· из каких этапов состоит жизненный цикл имитационного моделирования;

· задачах, решаемых на разных этапах жизненного цикла.

Вопросы темы:

1. Системный анализ и дискретно событийное моделирование.

2. Классификация моделей.

3. Метод Монте-Карло.

4. Жизненный цикл имитационного моделирования.

Вопрос 1. Системный анализ и дискретно событийное моделирование.

Имитационное моделирование осуществляется с помощью компьютера, поэтому для проведения расчета переменных модели требуется некоторая программа. Двумя основными способами для реализации имитационных моделей являются системный анализ и дискретно-событийное моделирование.

Системный анализ – моделирование непрерывных и дискретных процессов, основанное на применении математических моделей и численных методов.

Дискретно-событийное моделирование – имитация, осуществляемая в дискретные моменты, и основанная на обработке происходящих в эти моменты событий.

Под системным анализом в нашем рассмотрении мы подразумеваем совокупность математических методов моделирования на основе теории систем, созданных, начиная с начала 1960-х. На его основе могут создаваться как имитационные модели с непрерывным временем, так и имитационные модели с дискретным временем. Системное мышление и методы системного анализа отличаются изяществом и прошли проверку временем.

В теории управления применение системного анализа привело к возникновению новой области, известной под названием системной динамики, которая представляет собой, с одной стороны, методологию, когда система представляется как совокупность запасов и потоков, и, с другой стороны, набор инструментальных средств и методик для построения имитационных моделей сложных систем. Среди многих приложений методологии системной динамики особенно полезным является ее использование для решения вопросов стратегического характера на уровне предприятия.

Для поддержки процесса создания модели и проведения моделирования на основе системного анализа разработаны многочисленные программные средства. Многие из них позволяют пользователю самостоятельно конструировать модели с использованием графического интерфейса, что избавляет пользователя от необходимости самостоятельно составлять математические уравнения и применять численные методы для их решения. Эти средства сделали технологию доступной для широкого круга пользователей, а для решения разнообразных инженерных задач управления деловыми процессами появилась обширная литература (пример такого типа модели и ее результатов моделирования был ранее показан на Рис. 2).

Подход на основе моделирования дискретных событий весьма эффективен с точки зрения вычислительной сложности и имеет дополнительное преимущество, состоящее в том, что на интуитивном уровне он легко понятен. В его основе лежит довольно простая идея.

Вначале разработчик модели тем или иным образом (с помощью графического интерфейса или в программном коде) указывает последовательность действий и событий, происходящих в моделируемой системе.

Далее данные вводятся в программу, и, основываясь на моментах наступления событий, программный планировщик располагает все события в очереди. Имитация заключается в извлечении каждого события из очереди событий с последующим выполнением действия, соответствующего этому событию.

Например, для моделирования процесса выполнения заказа пользователь выбирает задачу или блоки для действий из палитры блоков, соединяет их вместе и определяет, как часто происходят события, и определяет частоту, с которой наступают события или сколько времени занимает выполнение соответствующего действия. В результате проведенной имитации можно собрать и обработать статистику о выполненных работах (действиях), имевших место расходах, а также оценить другие важные показатели. Более подробно реализация механизма дискретно-событийного моделирования будет рассмотрена далее.

Возможность построения имитационных моделей на основе графического интерфейса является весьма эффективным инструментом разработчика модели, которая в значительной степени способствовала широкому внедрению имитационного моделирования. Графическое представление можно разделить на две группы - блочные диаграммы и диаграммы состояний.

Блочные диаграммы представляют собой набор уравнений и последовательность вычислительных процедур. В этом случае применяется подход на основе системного анализа в комбинации с имитационным моделированием.

Диаграммы состояний представляют собой события и переходы между событиями, происходящие в моделируемой системе. В этом случае применяется дискретно-событийный подход.

Вопрос 2. Классификация моделей.

Имитационное моделирование используется для описания широкого спектра особенностей моделируемых систем и процессов в этих системах. С его помощью осуществляется воспроизведение (отображение) поведения моделируемой системы. Имитационное моделирование на компьютере может включать в себя все, начиная от простого сложения нескольких чисел до объемных вычислений, выполнить которые может оказаться не под силу даже самым быстрым современным вычислительным машинам. Модели для имитационного моделирования могут быть классифицированы по четырем различным признакам (Рис. 3).

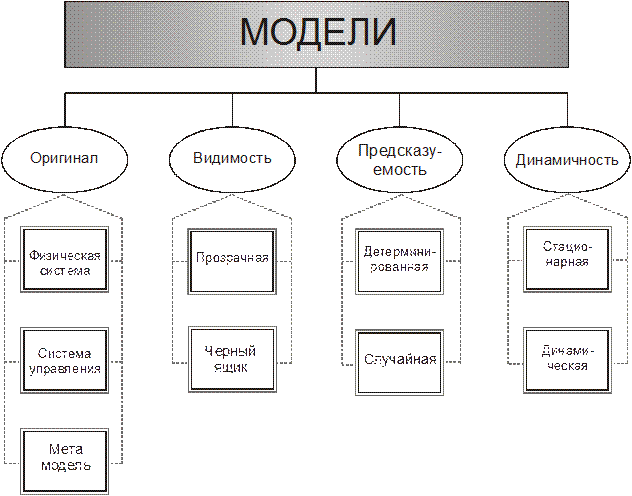
Рис. 3. Классификация моделей

Моделируемая система (оригинал).

Моделируемая система может принадлежать к одному из следующих типов:

· физическая система, например, цепочка поставок или производственная линия;

· система управления, например, CRM-процесс;

· метамодель, например, правила, которые позволяют установить, правильно ли составлена модель.

Видимость.

По своему внутреннему устройству модель может быть:

· прозрачная, то есть описывать реально существующие механизмы;

· «черный ящик», то есть, описывать такое же поведение, что и поведение реальной системы, но не моделировать структуру и функционирование реальных механизмов.

Предсказуемость

В зависимости от того, можно ли однозначно определить выход модели в какой-либо момент в будущем, модель может быть:

· Детерминированная, когда одному и тому же набору входных значений соответствует один набор значений результата.

· Случайная, когда один набор входных значений может привести к нескольким наборам выходных значений (выходы представляют собой вариации, которые описываются с помощью статистики).

Модели, поведение которых в будущем со всей определенностью предсказать нельзя, носят название стохастических. Этот термин используется в разных областях науки и означает непредсказуемость, хаотичность, случайность.

В модели стохастической системы итог не может быть предсказан по изначальному состоянию системы. Понятие определено в математической теории вероятностей.

Динамика.

С точки зрения постоянства выходных значений модель может быть:

· Стационарная, когда выход во времени и пространстве не меняется.

· Динамическая, когда выход во времени и пространстве меняется.

Моделируемая система.

Тип собираемой в процессе имитационного моделирования информации определяется изучаемой системой. Имитационное моделирование деловых процессов отличается от имитационного моделирования процессов, протекающих в той физической (материальной) системе, которая находится под управлением деловых процессов.

Например, при моделировании цепочек поставок необходимо моделировать физическую систему в части перемещения материальных объектов между узлами логистической сети. Это позволяет аналитику глубже представить себе динамику движения товарных запасов, выявить наличие и причины различных негативных эффектов и т. д.

В ряде случаев физическая система является основным изучаемым объектом при моделировании, например, для определения наилучшего местоположения центра дистрибуции или для того, чтобы оценить, насколько значительным будет влияние производительности отдельных единиц оборудования производственной линии на интегральную эффективность функционирования всей системы.

В других случаях главным объектом изучения является система управления и используемые в процессе управления данные. Например, моделирование процесса работы call-центра можно использовать для выявления потребностей в материальных и человеческих ресурсах, а также для поиска эффективных методов и процедур борьбы с перегрузками центра в пиковые периоды поступления вызовов.

Довольно часто на практике применяется имитационное моделирование на метамодели. Это может понадобиться, например, при проверке результата графического объединения моделей. Построение «модели моделей» полезно, когда акцент делается на архитектуре построения моделей, а не на поведении модели.

Прозрачность.

Прозрачность структуры модели для решения задач, связанных с организацией деловых процессов, имеет особое значение. Управленцам, как правило, нужно получить объяснения решений, которые им предлагает модель и которые, получаются, следовательно, автоматизированным способом. Для реализации этой возможности нужно обеспечить прозрачность структуры модели.

Вместе с тем, во многих ситуациях очень важно, чтобы модели позволяли получить лишь ответ и за возможно сжатое время. Такими возможностями обладают модели, управляемые данными, включая обычные регрессионные модели и более универсальные модели на основе нейронных сетей. Указанные модели можно создать и настроить довольно быстро при условии, что они будут обеспечены достаточно полными данными для определения внутренней их структуры. Такие модели относятся к моделям, построенным по типу «черного ящика» (Рис. 4).

Рис. 4. Модель типа «черный ящик»

Модели, построенные по типу «черного ящика», имеют свои собственные процедуры обучения и широко применяется на практике, поскольку отличаются простотой использования и высокой эффективностью. Подробнее модели этого типа рассматриваются в Вопросе 3 настоящей Темы.

Однако механизм получения результата в этих моделях скрыт. В этом смысле они очень похожи на человеческий мозг, то есть, мы не всегда знаем, внутренние законы протекания конкретного процесса рассуждения, но мы знаем, что это повторяется с большой эффективностью и регулярностью. Модели, построенные по типу «черного ящика», проходят обучение с использованием некоторых повторяющихся образцов и знания корреляции между данными. Модели имеют свой собственный внутренний механизм представления этих отношений. Внутреннее представление мало чем может помочь в построении цепочки причинно-следственных связей, которая является результатом поведения модели.

В противоположность этим моделям прозрачные (механистические) модели представляют собой явные описания реальных процессов, которые происходят на основе законов природы и научных принципах. Модели траектории полета ракеты, хорошо изученной химической реакции или управления запасами прозрачны в том смысле, что исследователь может обратиться к структуре самой модели, чтобы разобраться в поведении моделируемой системы. Все параметры механистической модели имеют содержательный смысл, который можно интерпретировать в терминах реальной системы, что позволяет лучше понять, как и почему был получен некоторый результат. С помощью таких моделей можно автоматически интерпретировать результаты и находить объяснения причин, вызывающих то или иное поведение моделируемой системы.

Вероятностные процессы.

Вероятностные процессы в моделировании играет такую же важную роль, как и в реальной жизни. Модели достаточных размера и сложности могут обладать целой совокупностью вариантов возможных поведений, и в общем случае неизвестно, как будет протекать моделируемый процесс до того момента, пока моделирование не начнется.

Для всех моделей существуют границы их применимости, определяющие области, в которых модель можно использовать для получения с ее помощью достаточно точных и надежных результатов относительно реальной системы. Все значения параметров, которые лежат за границами применимости, могут привести к результатам либо неточным, либо даже противоречащим реальным.

Для того чтобы можно было бы получить возможно более полное представление о поведении моделируемой системы, следует осуществлять имитационные эксперименты на модели (прогоны) при всех возможных условиях. В этом случае наборы входных параметров моделей, определяющие различные сценарии имитационных экспериментов, формируются случайным образом из статистических распределений. На основе этих наборов осуществляются прогоны имитационной модели, а затем полученные результаты подвергаются статистической обработке. Полученные итоговые величины используются для интегрального анализа всего возможного спектра поведения реальной системы, которые воспроизводятся моделью. Все приводимые выше примеры моделей можно представить как стохастические путем включения в их структуру механизмов случайного выбора значений параметров каждый раз, когда осуществляется прогон.

Например, в модели делового процесса, которая включает в себя среднее значение величины время обработки заказа, можно в каждом имитационном прогоне для значения время обработки заказа использовать случайную величину, получаемую выборкой из нормального закона распределения вероятностей с некоторыми значениями среднего и стандартного отклонения. В отсутствие случайных величин (т.е., в отсутствие действия случайных факторов) модель превращается в детерминированную. Иначе говоря, время обработки заказов в данном случае для каждого заказа независимо ни от чего всегда будет одним и тем же.

Динамика.

Наиболее важным свойством модели является ее динамика. Разработка модели представляет собой довольно непростую задачу, и многие используемые на практике модели создаются не как динамические, а как статические модели.

В частности, подавляющее большинство моделей, основанных на табличном представлении данных, являются по своей природе статическими. То же самое относится и к моделям, осуществляющим агрегирование или объединение данных.

Значительно больший эффект для решения задач анализа работы предприятия или прогноза возможных изменений в его функционирования в будущем можно получить с помощью модели, которая может показать изменения важных показателей поведения моделируемой системы с течением времени или в пространстве (например, географически).

Модели, воспроизводящие стационарный режим, могут дать полезные результаты, однако и они имеют недостаток, поскольку скрывают или искажают поведение реальной системы. Например, в условиях возникновения дефицита в цепочках поставок в них могут появляться резкие изменения, которые приводят к тому, что важная информация на модели получена не будет.

Модели можно использовать как в пакетном режиме, так и в оперативном режиме (онлайн), работа в котором рядом систем моделирования обеспечивается специальными средствами поддержки.

При проведении моделирования в пакетном режиме модель строится таким образом, что во время прогона доступ к реальным данным, объектам и событиям в реальном времени не устанавливается. Результаты моделирования могут использоваться для решения как стратегических, так и тактически задач, но временной интервал, в течение которого должно приниматься решение по этим задачам, достаточно велик (порядка нескольких недель или месяцев), так что прогоны модели могут вполне осуществляться в пакетном режиме. Данные, получаемые в результате прогонов модели, накапливаются в базах данных. При необходимости проводится независимый анализ, по полученным результатам готовится и публикуется отчет.

Применение моделей в оперативном режиме предполагает возможности получения моделью сведений о текущем состоянии протекающих процессов, происходящих событиях и циркулирующих в системе транзакциях (см. приводившиеся выше Рис. 1 и пояснения к рисунку). Это требует включения специальных средств поддержки отслеживания. Несмотря на то, что затраты на создание и поддержание этих средств могут быть весьма ощутимыми, во многих случаях эти затраты являются оправданными, поскольку эффект от применения моделей оказывается значительно их превосходящим.

Вопрос 3. Метод Монте-Карло.

Для изучения поведения системы в отсутствие знаний относительно последней (когда единственно возможным является представление системы в виде «черного ящика») может применяться метод статистических испытаний, или метод Монте-Карло. Этот метод является простейшим видом имитационного моделирования. Появление метода и его названия обязано работам фон Неймана и Улана, проводимым в конце 1940-х годов по экранированию ядерных излучений. Метод был известен и ранее, но широко распространяться под новым названием стал только одновременно с этими работами, которые велись под кодовым обозначением «Монте-Карло». Весьма успешно он применяется и в экономике.

Согласно методу Монте-Карло исследователь или проектировщик могут моделировать и исследовать поведение большой совокупности сложных систем на основе обработки статистических данных о работе этой системы. К таким статистическим данным могут относиться:

· случайные моменты времени прихода заказов или клиентов;

· величина загрузки производственных линий или участков;

· воздействия внешних факторов в виде требований, изменений в законах, штрафных санкций и др.;

· моментов времени поступление средств от заказчиков.

В качестве соответствующих им переменных могут использоваться число, совокупность чисел, вектор или функция. Метод Монте-Карло основан на статистических испытаниях и, являясь по своей сути численным методом, может применяться для решения полностью детерминированных задач, таких, как обращение матриц, решение дифференциальных уравнений в частных производных, отыскание экстремумов и численное интегрирование.

При вычислениях методом Монте-Карло статистические результаты получаются путем многократного проведения испытаний. Вероятность того, что эти результаты отличаются от истинных не более чем на заданную величину, есть функция количества испытаний.

В основе вычислений по методу Монте-Карло лежит случайный выбор чисел из заданного вероятностного распределения. При практических вычислениях эти числа берут из таблиц или получают путем некоторых операций, результатами которых являются псевдослучайные числа с теми же свойствами, что и числа, получаемые путем случайной выборки. Имеется большое число вычислительных алгоритмов, которые позволяют получить длинные последовательности псевдослучайных чисел (обсуждение этих вопросов будет вестись далее).

Применение метода Монте-Карло может дать существенный эффект при моделировании развития процессов, наблюдение которых в реальной системе нежелательно или невозможно, а другие математические методы исследования процессов либо не разработаны, либо неприемлемы из-за многочисленных оговорок и допущений, которые могут привести к серьезным погрешностям или неправильным выводам. В связи с этим необходимо не только наблюдать развитие процесса в нежелательных направлениях, но и оценивать гипотезы о параметрах нежелательных ситуаций, к которым приведет такое развитие, в том числе и параметрах рисков.

Вместе с тем, считать термин «метод Монте-Карло» синонимом термина «имитационное моделирование», как это будет видно из дальнейшего изложения, неверно. Метод Монте-Карло является важным, но вовсе не единственным компонентом методологии имитационного моделирования.

Вопрос 4. Жизненный цикл имитационного моделирования.

На Рис. 5 показан в укрупненном варианте процесс построения имитационной модели и проведения с ее помощью имитационных экспериментов.

Рис. 5. Проведение имитационных экспериментов

На первом шаге проводится уточнение целей моделирования, при этом программные средства не используются. Определение задач имеет очень большое значение и непосредственно определяет входные параметры модели, которые будут впоследствии варьироваться, и выходные параметры модели, которые будут анализироваться.

Постановка задачи может во многих случаях приобретать вид одного или нескольких вопросов, на которые должна ответить имитационная модель. Например, вопрос для имитационного моделирования работы цепочки поставок сети может быть сформулирован так: «Каким требованиям должна отвечать структура дистрибуторского центра, принятые для него правила обработки заказов и регламент пополнения запасов чтобы осуществлять обработку заказов и управление запасами, обеспечивая прибыльную работу и соблюдение в не менее чем 95% случаев сроков доставки комплектующих клиентам, в предположении 20%-ной точности прогноза?»

Здесь жирным шрифтом указаны входные параметры, которые можно изменять в имитационной модели, курсивом обозначены выходные параметры, которые можно наблюдать в виде результата прогона имитационной модели.

Возврат на предыдущие этапы может потребоваться в силу необходимости проверить корректность принятых решений при определении модели и формулировке деловой задачи. Правильный план проведения модельных экспериментов минимизирует их число, экономит затраты повышает надежность результатов.

В более детальном представлении жизненный цикл имитационного моделирования включает следующие основные этапы.

1) Формулировка проблемы.

Типичными задачами, как уже было отмечено, могут быть задачи оптимизации структуры и параметров физической системы, системы наблюдения и идентификации. На этом этапе определяются назначение модели, технология ее использования, место в технологическом контуре, требования к ее характеристикам. Результат этого этапа существенно влияет на содержательные требования к выполнению последующих этапов.

2) Структурный анализ процессов.

Задача этапа состоит в формализации структуры сложного реального процесса путем разложения его на процессы, выполняющие определенные функции и имеющие функциональные связи согласно легенде, разработанной экспертной группой. Выявленные подпроцессы, в свою очередь, могут подразделяться на другие функциональные подпроцесы общего моделируемого процесса.

Результат может быть представлен в виде графа, имеющего иерархическую многослойную структуру. В результате появляется формализованное изображение имитационной модели в графическом виде.

Структурный анализ особенно эффективен при моделировании деловых процессов, где в отличие от процессов материальных (физических) многие составляющие подпроцессы не имеют физической основы и протекают виртуально, поскольку оперируют с информацией, деньгами и логикой (законами) их обработки.

3) Формализованное описание модели.

На этом этапе преследуется цель получения графического изображения имитационной модели и формального описания функций, выполняемых каждым подпроцессом, условия взаимодействия всех подпроцессов. Особенности поведения моделируемого процесса (временная, пространственная и финансовая динамика) должны быть описаны на специальном языке для последующей трансляции. Для этого существуют различные способы.

При ручном способе для описания используется алгоритмический язык (язык программирования) типа GPSS, Pilgrim или Visual Basic.

При автоматизированном способе для описания используется компьютерного графический конструктор во время проведения структурного анализа, т.е. с очень незначительными затратами на программирование (в частности, такой конструктор, создающий описание модели, имеется в составе системы моделирования Pilgrim).

4) Подготовка данных.

Состоит в сборе и систематизации сведений о параметрах и характеристиках системы.

5) Построение (разработка) программной модели.

Этап заключается в трансляции и редактировании связей (сборке) модели, верификации (калибровке) параметров.

Трансляция может осуществляться в двух основных режимах.

В режиме интерпретации специальная универсальная программа, называемая интерпретатор на основании формализованного описания модели запускает все имитирующие подпрограммы программной модели.

Достоинством интерпретации является простота реализации.

Однако в этом случае отдельную моделирующую программу, которую можно было бы передать или продать заказчику, получить нельзя, что может в ряде случаев оказаться неприемлемым.

Примерами программных систем, построенных на основе интерпретации, являются системы GPSS, SLAM-II и ReThink.

В режиме компиляции обеспечивается возможность получения (на первом этапе) исполнительной программы имитации, которая далее используется для запуска имитационных прогонов (на втором этапе). Реализация этого режима сложнее, но это не отражается на процессе разработки модели. В результате можно получить отдельную программную модель, которая работает независимо от системы моделирования в виде отдельного программного продукта. Вместе с тем, в случае простых моделей, которые подвергаются интенсивным корректировкам в процессе работы с ними, такой режим может оказаться менее предпочтительным по сравнению с режимом интерпретации.

Примером программной системы, построенной на основе интерпретации, является системы Pilgrim.

6) Оценка адекватности модели.

Состоит в установлении степени соответствия результатов, получаемых на построенной и реализованной модели, результатам, получаемым на аналогичных наборах входных данных в реальной системе.

В зависимости от характера задач, моделируемых процессов и специфических особенностей модели могут применяться различные критерии адекватности.

7) Проведение экспериментов на модели.

Включает этапы планирования и реализации эксперимента. Для моделей среднего и крупного размера, рассчитанных на проведение большого числа прогонов, используются специальные методы планирования эксперимента.

8) Документирование результатов.

В зависимости от целей моделирования формами документов могут быть научные отчеты, статьи, пояснительные записки и доклады руководству и т.п.

Из наиболее сложных проблем, которые необходимо решать в процессе определения модели, следует отметить следующие:

· выбор типа модели, соответствующего задаче;

· идентификацию протекающих в моделируемой системе процессов;

· установление нужного уровня детализации представления или точности;

· выбор способа абстрактного представления процессов;

· сбор данных для ввода в модель.

Тип модели должен выбираться исходя из плюсов и минусов, о которых речь шла выше.

Для идентификации процессов, определения уровня детализации и способа описания могут использоваться типовые описания (шаблоны) или средства, которые позволяет определить собственные шаблоны. Полезно использовать типовые модели и стандарты, которые содержат описания типовых процессов и упрощают процессы создания модели и проведения имитационных исследований.

Этап сбора и организации данных часто является узким местом процесса моделирования. Если не позаботиться об использования эффективных методов работы с данными, то могут возникнуть проблемы как с получением нужных данных у пользователей, так и с подготовкой собранных данных для их ввода в модель. В зависимости от размера модели, может понадобиться большой объем данных, сбор которых может вылиться в очень длительный процесс, причем, значительная часть данных, имеющих слишком большую степень детализации, может оказаться в конце процесса сбора так и не полученной. Такая ситуация, которая может служить основной причиной неудачи моделирования, является примером проявления неразумной и нереальной цели моделировать все.

Для случая больших моделей имеет смысл организовать работу с ними так, чтобы в самом начале создать работоспособную и несложную модель. Дальнейшая работа с моделью может быстро выявить, какие данные требуются дополнительно к тем, что есть, и какие требуют большей детализации.

Опытные специалисты имеют, как правило, хорошее представление о моделируемой системе и структурируют данные для моделирования таким образом, что для начала работы с моделью нужно только ограниченное число данных. Эти данные обеспечивают возможность качественного обоснования корректности модели быть достаточно для достижения хорошей качественной проверки модели, которые затем последовательно уточняются. Кроме того, такой подход позволяет провести на основе полученных результатов уточнение первоначальной формулировки задачи на моделирование и составить рациональный план проведения модельных экспериментов.

Для структурирования и организации имитационных экспериментов используются методы планирования эксперимента. Методы планирования представляют собой пошаговый план проведения, изучения и оценивания результатов имитационных экспериментов. Ряд программных средств обеспечивает возможность настройки параметров запуска имитационной модели непосредственно в моделирующей среде.

Выводы:

1. Основными подходами к построению имитационных моделей являются подход на основе системной динамики и дискретно событийное моделирование. Второй подход является более предпочтительным в случае необходимости детального учета особенностей моделируемых процессов.

2. Модели систем могут классифицироваться по различным признакам. Экономические процессы представляются динамическими стохастическими моделями с прозрачной структурой и используются для имитации процессов, протекающих как в физической системе, так и в системе управления.

3. Для изучения систем в отсутствие достаточных знаний об их структуре и законах поведения может применяться метод Монте-Карло, представляющий собой простейший вид имитационного моделирования. Применение метода может быть эффективным в случаях, когда изучение процессов в реальной системе нежелательно или невозможно, а другие математические методы исследования отсутствуют.

4. Процесс создания имитационной модели проходит через логическую последовательность этапов. Моделирование носит итеративный характер, предполагающий возможность возврата после выполнения некоторого этапа на один из предшествующих.

5. Задачи, решаемые на отдельных этапах моделирования, может отличать высокая сложность. Для решения этих задач используются методы из разных областей знаний, таких как теория систем, системный анализ, теория вероятностей, математическая статистика, теория планирования эксперимента и других.

Вопросы для самопроверки:

1. Какие существуют способы реализации имитационных моделей?

2. В чем состоит сущность моделирования на основе системного анализа?

3. В чем состоит сущность дискретно-событийного моделирования?

4. Какие возможности разработчику модели и экспериментатору предоставляет графический интерфейс?

5. Что понимается под блочными диаграммами?

6. Что понимается под диаграммами состояний?

7. По каким признакам могут классифицироваться модели?

8. На какие классы можно подразделить модели в зависимости от моделируемой системы?

9. На какие классы можно подразделить модели в зависимости от учета в модели внутреннего устройства?

10. На какие классы можно подразделить модели в зависимости от возможности предсказать выход модели в какой-либо момент в будущем?

11. На какие классы можно подразделить модели в зависимости от изменчивости выходных значений?

12. В каких основных режимах можно использовать имитационную модель?

13. Какие задачи при запусках имитационных моделей в пакетном режиме?

14. Какие задачи при запусках имитационных моделей в оперативном режиме?

15. Что такое метод Монте-Карло?

16. Задачи какого типа могут решаться методом Монте-Карло?

17. Как имитируются действие случайных факторов при реализации на компьютере метода Монте-Карло?

18. В каких случаях метод Монте-Карло может дать особенно большой эффект?

19. Из каких основных этапов состоит жизненный цикл имитационного моделирования?

20. Что такое режим интерпретации модели?

21. Что такое режим компиляции модели?

22. Каковы достоинства и недостатки режима интерпретации?

23. Каковы достоинства и недостатки режима компиляции?

24. Что можно отнести к наиболее сложным проблемам, решаемым на этапе определения (описания) модели?

25. Какой прием можно применить для упрощения идентификации процессов моделируемой системы?

26. Какой принцип практической реализации модели целесообразно применять?

27. Приведите пример формулировки типичной задачи имитационного эксперимента.

Литература по теме:

Основная литература:

Дополнительная литература:

1. Советов Б.Я., Яковлев С.А. Моделирование систем. – М.: Высшая школа, 2003 – 320 с.

2. Форрестер Дж. Мировая динамика. – М.: Наука, 1978. – 168 с.

3. Шенон Р. Имитационное моделирование систем - искусство и наука. – М.: Мир, 1978 – 424 с.

Практические задания:

1. Для процессов объекта, который был вами выбран для анализа в задании к Теме 1, сформулируйте одну или несколько задач для имитационного моделирования (по примеру, приведенному в Вопросе 4 настоящей Темы).

Тема 3. Механизмы модельной динамики

Цели изучения темы:

· изучить методы имитации протекания процессов во времени.

Задачи изучения темы:

· познакомиться с принципами динамической имитации;

· понять логику и последовательность действий, обеспечивающих динамическую имитацию.

Успешно изучив тему, Вы:

Получите представление о:

· методе пошаговой имитации;

· методе событийной имитации;

· алгоритме планирования событий;

· методе кусочно-линейной аппроксимации непрерывных процессов.

Будете знать:

· как работает планировщик событий программной модели;

· как имитируется в цифровых компьютерах протекание непрерывных процессов.

Вопросы темы:

1. Аналитическая модель.

2. Пошаговая имитация.

3. Дискретно-событийная имитация.

4. Алгоритм планирования событий.

5. Имитация процессов с непрерывным множеством состояний.

Вопрос 1. Аналитическая модель.

Пусть нам необходимо проанализировать работу службы технического обслуживания. Будем полагать, что прием заявок на обслуживание осуществляет один оператор, и клиенты (сотрудники подразделений предприятия) приходят к нему со своими заявками. Если оператор занят обслуживанием другого клиента, очередной обратившийся клиент становится в очередь (Рис. 6).

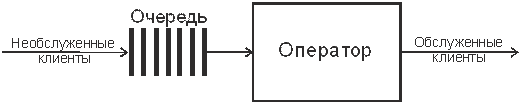
Рис. 6. Структура центра обслуживания клиентов

Будем вначале полагать, что величина интервалов времени между приходами клиентов в рассматриваемый центр технического обслуживания подчиняется экспоненциальному закону распределения. Это распределение играет важную роль в проведении системного анализа деловой деятельности и используется для имитации потоков во многих случаях, поэтому рассмотрим его подробнее.

Если вероятность наступления события на малом интервале времени Δt очень мала и не зависит от наступления других событий, то интервалы времени между двумя последовательными событиями распределяются по экспоненциальному закону с плотностью вероятностей:

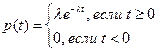
Особенностью этого распределения является свойство его параметров. Поскольку математическое ожидание и дисперсия , то .

Иначе говоря, математическое ожидание случайной величины, распределенной по экспоненциальному закону, равно среднеквадратичному отклонению, что является одним из основных свойств экспоненциального распределения.

Экспоненциальному закону подчиняются многие реально протекающие процессы, например:

· интервалы времени между поступлениями заказов на предприятие;

· интервалы времени между приходами покупателей в супермаркет;

· продолжительность телефонных разговоров;

· срок службы узлов компьютера (работающего, например, в бухгалтерии).

Поясним механизм возникновения этого распределения. На Рис. 7 показана диаграмма, соответствующая случаю, когда несколько (k) независимых потоков сливаются в один.

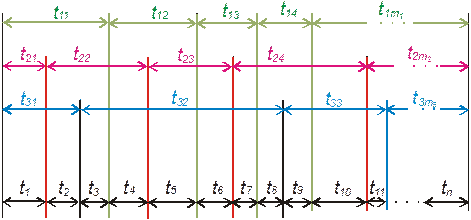
Рис. 7. Суперпозиция потоков

В каждом из потоков можно наблюдать элементарных событий, i=1.....k (например, приходов клиентов в центр обслуживания). Интервалы времени между событиями - независимые случайные величины, распределенные по неизвестному закону с математическим ожиданием 1/λ.

Если теперь спроектировать моменты наступления всех событий на одну общую ось времени и рассмотреть случайные интервалы времени между двумя последовательно наступающими событиями полученного суммарного потока, состоящего из n событий

то (доказывается математически) образованный таким образом поток подчиняется экспоненциальному закону распределению.

Поток, в котором интервалы между событиями имеют экспоненциальное распределение, носит название простейшего. Своим названием этот поток обязан тому обстоятельству, что потоки с этим распределением значительно упрощают построение аналитических моделей, которые можно использовать в ряде практических случаев. Построением и исследованием аналитических моделей занимается теория массового обслуживания.

Предположим для примера, что клиентами некой крупной компании являются физические и юридические лица. Несмотря на то, что каждый из них может иметь собственную программу работ на значительный временной интервал, суммарный поток обращений клиентов в компанию характеризуется случайной величиной интервала времени между двумя последовательными обращениями, распределенной по экспоненциальному закону.

Вернемся к нашей модели. Если входящий поток клиентов представляет собой простейший поток, то среднее время ожидания клиентов в очереди в такой системе можно определить по формуле Хинчина-Полачека:

где

- среднее время ожидания клиентов в очереди;

- среднее время обслуживания у оператора;

- коэффициент загрузки оператора;

- коэффициент вариации времени обслуживания.

Коэффициент загрузки оператора можно найти как

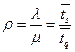где

- средний интервал между клиентами во входящем потоке.

Коэффициент вариации времени обслуживания определяется как

где

- среднеквадратическое отклонение времени обслуживания.

С возрастанием загрузки оператора (т.е., чем ближе среднее время обслуживания к среднему интервалу поступления клиентов), как видно формулы, растет время задержки в очереди .

Если время обслуживания оператором всегда одинаково, то и

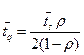
Если время обслуживания имеет экспоненциальное распределение, то (свойство экспоненциального распределения) и

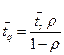
Однако применить эту формулу можно только в случае, когда поток приходящих клиентов является простейшим. Имитационная модель на свои параметры никаких ограничений не имеет.

Вопрос 2. Пошаговая имитация.

Чтобы разобраться в том, на каких основах строятся программы имитации, и как в них имитируется протекание реального времени, рассмотрим пример модели исследуемой системы.

Предположим, что перед нами стоит задача определения среднего числа клиентов, одновременно находящихся в приемной службы технического обслуживания (в очереди и у оператора), что может быть важно с точки зрения эффективности обслуживания клиентов (хотя бы с целью определить подходящее число кресел для ожидающих клиентов). С этой целью проведено обследование процесса обслуживания.

Результаты обследования представлены в Табл. 1, где в первой строке проставлены моменты времени прихода очередного клиента, а во второй продолжительность приема и регистрации заявки на обслуживание оператором (то и другое в минутах).

Таблица 1.

Приход	0	2	6	11	12	19	22	26	36	38	45	47	49	52	61
Прием	5	7	1	9	2	4	4	3	1	2	5	4	1	2	1

Для получения нужного результата построим на основе собранных данных другую таблицу (Табл. 2), в которой столбец t будет обозначать текущее время, столбец Приход – момент ожидаемого прихода очередного клиента, столбец Уход – момент ожидаемого окончания обслуживания клиента оператором, столбец N – число клиентов, находящихся в данный момент на приеме у оператора.

Таблица 2.

t	Приход	Уход	N
0	2	5	1
1	2	5	1
2	6	5	2
3	6	5	2
4	6	5	2
5	6	12	1
6	11	12	2
7	11	12	2
8	11	12	2
9	11	12	2
10	11	12	2
11	12	12	3
12	19	13	3
13	19	22	2
14	19	22	2
15	19	22	2
16	19	22	2
17	19	22	2
18	19	22	2
19	22	22	3
20	22	22	3
21	22	22	3
22	26	24	3
23	26	24	3
24	26	28	2
25	26	28	2
26	36	28	3
27	36	28	3
28	36	32	2
29	36	32	2
30	36	32	2
31	36	32	2
32	36	35	1
33	36	35	1
34	36	35	1
35	36	–	0
36	38	37	1
37	38	–	0
38	45	40	1
39	45	40	1
40	45	–	0
41	45	–	0
42	45	–	0
43	45	–	0
44	45	–	0
45	47	50	1
46	47	50	1
47	49	50	2
48	49	50	2
49	52	50	3
50	52	54	2
51	52	54	2
52	61	54	3
53	61	54	3
54	61	55	2
55	61	57	1
56	61	57	1
57	61	–	0
58	61	–	0
59	61	–	0
60	61	–	0
61	¥	62	1
62	¥	–	0

Прочерк («–») означает, что событие (Уход или Приход) на данный момент не определено.

Содержимое столбца N обновляется в моменты приходов и уходов клиентов увеличением или уменьшением на единицу соответственно.

Теперь на основании этой таблицы несложно определить интересующий нас показатель. Среднее для дискретной случайной величины согласно определению находится как:

В нашем случае величина i в процессе наблюдения принимала значения, как видно из Табл. 2, из набора 0, 1, 2, 3 (столбец N).

Значения вероятностей p(i) нахождения в очереди i , i=0, …, 3 клиентов несложно найти, определив число строк, содержащих в столбце N Табл. 2 значение i (что означает величину суммарного временного промежутка нахождения в очереди i клиентов), и поделив найденное число строк на 62 (т.е., на весь период наблюдения). Подставляя в формулу, получим:

Рассмотренный нами способ представления протекания процессов во времени лежит в основе пошагового метода моделирования. В данном примере в качестве значения шага была выбрана одна минута реального времени. Работа алгоритма, который используется для имитации процессов в компьютерной программе, состоит, как мы сейчас имели возможность наблюдать, к повторению одной и той же последовательности действий:

· перемещению модельных часов на величину шага;

· проверки того, наступило ли в этот (новый) момент какое-либо событие;

· определению значений моментов наступления очередного события в случае, если событие этого типа наступило;

· обновлению параметров состояния процессов (в данном случае, параметра N - числа заявок в приемной).

Работа алгоритма продолжается до выполнения условий окончания моделирования, которые обычно задаются в виде достижения заданного времени моделирования.

Вопрос 3. Дискретно-событийная имитация.

Описанный выше алгоритм имеет два очевидных недостатка.

Во-первых, он весьма неэффективен: даже на приведенном примере видно, что строки с повторяющимися значениями составляют большую долю среди всех строк. Изменения значений в строках происходят только в моменты прихода очередного клиента или завершения обслуживания клиента, находящегося у оператора. Это означает, что компьютерная программа будет выполнять много шагов вхолостую, не производя никаких действий.

Во-вторых, в отличие от рассмотренной ситуации, где выбор минуты в качестве шага естественным образом следовал из имеющихся исходных данных, в реальной ситуации возникает необходимость определять величину шага. Это обусловлено различием в диапазонах изменения временных величин и возможностью принимать произвольные значения внутри интервала.

Поэтому на практике обычно применяется дискретно-событийный метод имитации протекания процессов. В этом случае перемещение модельного времени совершается не на один и тот же шаг, а на момент времени, соответствующий наступлению следующего (ближайшего) события.

Для рассмотренного примера это будет означать представление, показанное в Табл. 3, которая получена из Табл. 2 выборкой из последней только тех строк, в которых менялось содержимое в связи с происшедшими событиями, т.е., в моменты прихода и/или ухода клиента.

Таблица 3.

t	Приход	Уход	N
0	2	5	1
2	6	5	2
3	6	5	2
4	6	5	2
6	11	12	2
11	12	12	3
12	19	13	3
19	22	22	3
22	26	24	3
24	26	28	2
26	36	28	3
28	36	32	2
32	36	35	1
35	36	–	0
36	38	37	1
37	38	–	0
38	45	40	1
40	45	–	0
45	47	50	1
47	49	50	2
49	52	50	3
50	52	54	2
52	61	54	3
54	61	55	2
55	61	57	1
57	61	–	0
61	¥	62	1
62	¥	–	0

Построение Табл. 3 по содержимому Табл. 2 в данном примере, разумеется, не означает, что практически работа ведется именно таким образом. На самом деле дискретно-событийная имитация производится в программах впрямую и программных системах моделирования используются различные способы реализации этого механизма.

Вопрос 4. Алгоритм планирования событий.

Разделим все происходящие события на группу безусловных и группу условных событий.

К безусловным событиям отнесем события, которые наступают безотносительно к тому, наступают или не наступают какие-либо другие события. К таким событиям, в частности, относятся приходы клиентов в центр обслуживания.

К условным событиям отнесем события, которые наступают только в моменты, когда для них появляются соответствующие условия. Таким событием, в частности, является начало обслуживания очередного клиента оператором, поскольку это возможно лишь тогда, когда в очереди есть ждущие клиенты и оператор не занят обслуживанием другого клиента.

Обычно к условным относятся события, связанные с началом какой-либо деятельности (работы).

Рассмотрим чуть более сложный вариант центра обслуживания, в котором заявки клиентов могут относиться к одному из двух типов (1 или 2), и обслуживанием каждого типа заявок занимается выделенный оператор (Рис. 8).

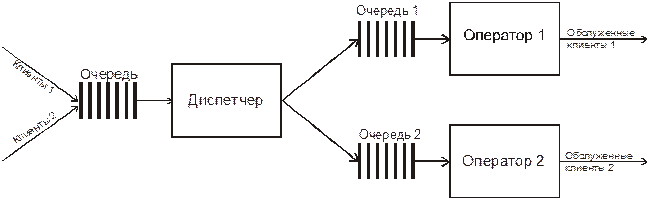
Рис. 8. Центр обслуживания с двумя операторами

Клиенты, обращающиеся с заявками типа 1, приходят с интервалом 10 минут, а клиенты, обращающиеся с заявками типа 2, приходят с интервалом 20 минут. Пришедший клиент становится в очередь к диспетчеру, который направляет клиента к нужному ему оператору. На рассмотрение заявки диспетчер затрачивает 2 минуты. Оператор, обрабатывающий заявки типа 1, тратит на каждую 8 минут, оператор, обрабатывающий заявки типа 2, тратит на каждую 14 минут.

Определим вначале все безусловные (Б) события (Табл. 4) и условные (У) события (Табл. 5).

Таблица 4.

Событие	Тип	Состояние	Будущие события
Б1	Приход	Клиент типа 1 входит в очередь к диспетчеру	Б1
Б2	Приход	Клиент типа 2 входит в очередь к диспетчеру	Б2
Б3	Завершение обслуживания	Диспетчер завершает рассмотрение заявки и направляет клиента 1 к оператору 1, клиента 2 к оператору 2
Б4	Завершение обслуживания	Оператор 1 завершает обработку (счетчик числа выполненных работ увеличивается на 1)
Б5	Завершение обслуживания	Оператор 2 завершает обработку (счетчик числа выполненных работ увеличивается на 1)

Таблица 5.

Событие	Тип	Условие	Состояние	Будущие события
У1	Начало обслуживания	Очередь диспетчера не пуста и диспетчер свободен	Диспетчер берет клиента из очереди к диспетчеру на обслуживание	Б3
У2	Начало обслуживания	Очередь оператора 1 не пуста и оператор 1 свободен	Оператор 1 берет клиента из очереди к оператору 1 на обслуживание	Б4
У3	Начало обслуживания	Очередь оператора 2 не пуста и оператор 2 свободен	Оператор 2 берет клиента из очереди к оператору 2 на обслуживание	Б5

Алгоритм, который можно применить для имитации процессов поясняется на Рис. 9.

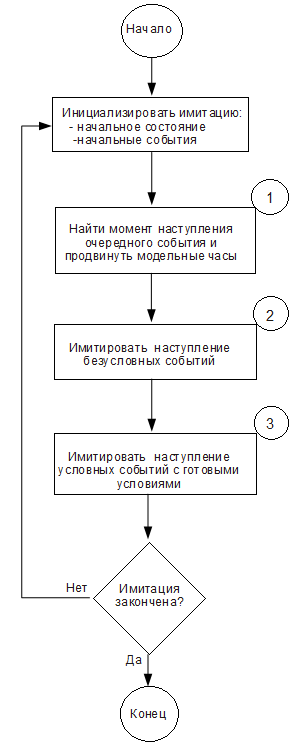
Рис. 9. Алгоритм планирования событий

В начале имитации устанавливается начальное состояние процесса. Например, можно задать определенное число уже ждущих в очередях клиентов и промежутки времени, остающиеся до завершения обслуживания клиентов диспетчером и/или операторами. Аналогично определяются моменты наступления безусловных событий, в частности, моменты прихода первых клиентов типа 1 и типа 2.

На шаге 1 имитации делается просмотр списка событий, и модельные часы перемещаются на время ближайшего по времени наступления события.

На шаге 2 имитации имитируются результаты наступления всех безусловных событий.

На шаге 3 проверяется возможность имитации наступления условных событий, после чего имитируются результаты наступления тех из них, для которых условия наступления в данный момент выполнены. Поскольку наступление какого-либо из событий может привести к тому, что будут созданы условия для наступления другого события, проверки после каждого раза необходимо повторять вплоть до момента, пока для всех событий списка будет установлен факт отсутствия условий их наступления.

Если проверка условий окончания имитации дает отрицательный ответ (например, может быть достигнут установленный порог модельного времени или числа пришедших/обслуженных клиентов), то вся описанная последовательность шагов повторяется.

Вопрос 5. Имитация процессов с непрерывным множеством состояний.

Операции, выполняемые во многих реальных процессах и системах, нельзя охарактеризовать только скачкообразным изменением их состояния, поскольку состояние системы меняется со временем непрерывно. Одним из наиболее показательных примеров может служить поток движущейся жидкости, который можно наблюдать на химических или нефтеперерабатывающих заводах. Заполнение резервуаров, в которых хранятся продукты переработки в этих системах, представляет собой непрерывный во времени процесс.

В более общем случае любые системы, в которых присутствуют процессы быстрого перемещения больших объемов каких-либо элементов или объектов можно рассматривать как непрерывные. Примерами таких систем являются заводы по производству пищевых продуктов и системы связи.

Будет ли изучаемая система рассматриваться как дискретная или непрерывная, определяется в каждом случае уровнем детализации, на котором должна анализироваться система.

Имитировать непрерывные изменения состояний цифровые компьютеры не могут. Поэтому имитацию процессов с непрерывно изменяющимся состоянием нужно осуществлять либо с использованием другого класса вычислительных машин, называемых аналоговыми, либо разбивая временной интервал на большое число небольших интервалов Δt. Чем меньше величина временного интервала (шага), тем более точным будет приближение, но тем медленнее будет протекать процесс имитации, поскольку пересчеты текущей величины уровня будут делаться чаще.

Более рациональный подход учитывает величину изменения состояния процесса (Рис. 10).

Рис. 10. Дискретная аппроксимация непрерывных процессов

На рисунке видно, как можно построить модель процесса изменения уровня жидкости в резервуаре с течением времени, если принять в рассмотрение характер изменения реального процесса. В этом примере изменения состояния во времени подвергаются линейной аппроксимации.

Этот метод, как нетрудно видеть, с точки зрения типа получаемого результата аналогичен методу квантования времени, описанному выше.

Непрерывное моделирование широко используется в целом ряде областей и, в частности, экономике. Ряд пакетов дискретно-событийного моделирования имеют также возможности для моделирования непрерывных процессов, хотя имитировать непрерывные процессы можно и в пакетах без этой опции. Это реализуется включением в описание модели регулярно повторяющегося события, которое наступает с временным шагом Δt.

Такой подход бывает необходимо применять довольно часто, поскольку существует много реальных случаев, когда изменения происходят как дискретно, так и непрерывно, так, что нужно рассматривать оба типа процессов в их комбинации. Например, сбои и поломки в работе оборудования (дискретные изменения) в процессе протекания основного технологического процесса на химическом заводе (непрерывное изменение).

Существует ряд ситуаций, в которых в качестве альтернативы дискретно-событийному моделированию может применяться подход на основе системной динамики. В частности, как тот, так и другой подходы можно использовать для моделирования процессов в цепочках поставок.

Примеров подхода к моделированию на основе использования комбинации обоих названных не очень много. Одним из таких примеров является система Anylogic (http://www.xjtek.ru/) .

В общем случае, дискретно-событийное моделирование целесообразно использовать тогда, когда в модели системы требуется отразить множество деталей ее структуры и функционирования, в частности, когда нужно отследить работу отдельных элементов, образующих систему.

Выводы:

1. Компьютерная имитация протекания реальных процессов нуждается в методах моделирования системного времени. Из существующих алгоритмов, реализующих эту функцию, наибольшей эффективностью обладает алгоритм планирования событий на основе дискретно-событийной имитации.

2. Имитация событий с непрерывным множеством состояний на цифровых компьютерах принципиально невозможна, поэтому решение этой задачи требует специальных методов. Типичным методами являются метод квантования и кусочно-линейной аппроксимации реального процесса.

3. Экономические процессы часто характеризуются присутствием в них как дискретной, так и непрерывной компонент. По этой причине ряд пакетов моделирования обладает возможностью имитировать процессы, представляющие собой комбинации процессов различных типов.

Вопросы для самопроверки:

1. Какую специфическую задачу требуется решать в программных моделях, используемых для имитации?

2. В чем состоит сущность метода пошагового моделирования?

3. Каковы недостатки метода пошагового моделирования?

4. Какая идея лежит в основе дискретно-событийного метода имитации протекания процессов?

5. На какие группы подразделяются события в случае применения алгоритма планирования событий?

6. Что такое безусловные события?

7. Что такое условные события?

8. Из каких основных действий состоит алгоритм планирования и в какой логической последовательности они выполняются?

9. Чем характеризуется процесс с непрерывным множеством состояний?

10. Приведите примеры реальных процессов с непрерывным множеством состояний?

11. Какой основной принцип используется для отнесения моделируемых процессов к дискретным или непрерывным?

12. Какие существуют основные методы моделирования непрерывных процессов?

13. Каким образом может реализовываться в программах (пакетах) моделирования возможность одновременной имитации как дискретных, так и непрерывных процессов?

Литература по теме:

Основная литература:

2. Н.Н. Снетков Имитационное моделирование экономических процессов. Учебно-практическое пособие –М.: Изд. центр ЕАОИ, 2008. – 228 с.

Дополнительная литература:

1. Шенон Р. Имитационное моделирование систем - искусство и наука. – М.: Мир, 1978 – 424 с.

Практические задания:

1. С целью оценить качество формируемого плана полетов руководство аэропорта, имеющего одну взлетно-посадочную полосу, хочет получить предварительную оценку ситуации, которая сложится в аэродромной зоне воздушного пространства и в зоне предварительного старта аэропорта. Для этого руководство хочет оценить среднее число воздушных судов, которые будут ждать разрешения диспетчера на посадку в зоне ожидания, и среднее число воздушных судов, которые будут ждать разрешения диспетчера на взлет в зоне предварительного старта.

Кроме того, руководство хочет выяснить также, насколько плотно будет загружена взлетно-посадочная полоса, поскольку она представляет собой дорогостоящий ресурс.

Для простоты можно считать, что время как взлета, так и посадки вместе с безопасным интервалом между последовательными взлетами/посадками (т.е., время занятости взлетно-посадочной полосы) составляет ровно две минуты.

В случае, если в зоне ожидания (посадки) есть воздушное судно, оно имеет приоритет перед воздушным судном, ожидающим разрешения на взлет. Время на подлет из зоны ожидания к взлетно-посадочной полосе после получения команды диспетчера на посадку не учитывается.

Фрагмент оцениваемого плана полетов (первого часа суток) выглядит следующим образом:

Вылет	0	2	6	11	13	19	22	26	36	38	45	47	49	52	60
Прилет	2	4	7	12	14	18	21	24	32	35	41	47	48	51	59

В верхней строке обозначены моменты (минуты) плановых вылетов воздушных судов из аэропорта, в нижней строке - моменты (минуты) плановых приземлений прилетающих воздушных судов.

а) Постройте таблицу пошаговой имитации для процессов взлетов-посадок и определите:

· среднее значение числа воздушных судов, ожидающих разрешения на посадку;

· среднее значение числа воздушных судов, ожидающих разрешения на взлет;

· коэффициент простоя взлетно-посадочной полосы, определяемый как отношение времени простоя ко всему времени наблюдения.

б) Разработайте списки условных и безусловных событий для алгоритма планирования событий в имитационной модели.

Тема 4. Имитация случайных факторов

Цели изучения темы:

· изучить методы и приемы получения случайных величин, используемых в компьютерной имитации.

Задачи изучения темы:

· понять содержательный смысл задачи имитации изменчивого поведения реальных процессов;

· изучить основные приемы имитации параметров случайных величин, описывающих протекание и параметры моделируемых процессов.

Успешно изучив тему, Вы:

получите представление о:

· способах использования случайных чисел для использования в компьютерных моделях;

· понятии псевдослучайного числа;

· устройстве программных генераторов псевдослучайных чисел.

Будете знать:

· как применяются случайные числа для имитации значений случайных параметров реальных процессов на основе данных наблюдения;

· как применяются случайные числа для имитации значений случайных параметров реальных процессов на основе теоретических распределений;

· что представляет собой нормальный закон распределения вероятностей, и в каких случаях следует его применять.

Вопросы темы:

1. Изменчивость поведения и случайные числа.

2. Моделирование изменчивости с помощью случайных чисел.

3. Выборки из теоретических распределений.

4. Компьютерная генерация псевдослучайных чисел.

Вопрос 1. Изменчивость поведения и случайные числа.

После рассмотрения способа имитации протекания процессов времени, рассмотрим второй вопрос, который играет центральную роль в реализации имитационных процессов, а именно, способы моделировании вероятностного характера поведения модели.

Поскольку большинство из практически встречающихся моделей относится к моделям случайным, то моделирование непредсказуемых изменений в протекании процессов представляет собой крайне важную задачу.

Ранее при имитации работы центра обслуживания в модель не включались какие-либо элементы, отражающие изменчивость в протекании процесса, которая на самом деле имеет место. В частности, было бы неправильно считать время, которое абоненты тратят каждый раз на определение адресата их заявки и на обслуживание их заявки операторами, одинаковым.

Аналогичным образом, число пришедших запросов за какой-то промежуток времени, начавшийся в одно время дня, не будет в общем случае тем же самым, что и число пришедших запросов за какой-то промежуток времени, начавшийся в другое время дня.

Для выяснения вопроса о том, как может такая непредсказуемая изменчивость быть представлена в имитационной модели, будем для начала считать, что клиенты приходят точно с интервалом 3 минуты. Но каждый клиент может быть отнесен либо к типу 1, либо к типу 2 в зависимости от того, заявку на какое обслуживание он намерен оставить.

Простым способом определения типа вызова в отсутствие компьютера было бы бросание жребия (или монеты) каждый раз, когда клиент появляется в модели: орел может означать тип 1, решка – тип 2.

Недостатком такого подхода является то, что он предполагает равные доли клиентов типа 1 и типа 2 (если только центр тяжести монеты не смещен).

Предположим, что к типу 1 относится 60% клиентов, а к типу 2 – 40%. Тогда «физическую модель» можно представить помещенными в урну 10 листками бумаги с записанным на шести из них числом 1, а на оставшихся четырех числом 2. В момент прихода очередного клиента для определения типа клиента из урны будет доставаться листок с записанным на нем номером, после чего листок будет в урну возвращен, что обеспечит неизменность соотношения типов клиентов как 60:40.

Однако такой подход можно использовать только в случае физической (материальной) модели, поскольку выбирать листки из урны компьютер не умеет. Аналогичный принцип в компьютерном моделировании реализуется на основе использования случайных чисел.

Случайные числа представляют собой последовательности чисел, которые появляются в случайном порядке. Они могут быть либо целыми числами, принадлежащими какому-то диапазону, скажем, от 0 до 9 или от 0 до 99, или вещественными (действительными) числами (имеющими десятичные знаки) в диапазоне от 0 до 1.

Последовательность целых случайных чисел, принадлежащих диапазону 0-99, можно создать, поместив 100 бумажных листков в урну, на каждом из которых будет записано одно число, извлекая из урны каждый раз, когда требуется, один листок. Листок бумаги возвращается потом на свое место.

Случайные числа, которые получены таким образом, обладают двумя важными свойствами:

· равномерность, состоящая в том, что вероятность появления любого из чисел последовательности при каждом извлечении одна и та же;

· независимость, состоящая в том, что выборка одного из чисел никак не влияет на вероятность выборки этого же или другого числа при следующем извлечении листка с номером.

Соблюдение этих свойств обеспечивается тем, что листки каждый раз возвращаются на свое место.

В Табл. 6 приведены значения случайных чисел, равномерно распределенных в промежутке 0-100.

Таблица 6.

Целые числа, равномерно распределенные в промежутке 0-100

0 9

Таблицы типа приведенной выше можно получить из общедоступных («бумажных») источников (справочники по математике, теории вероятностей или математической статистике) или в программах типа электронных таблиц с помощью встроенных в них специальных функций (например, функции СЛУЧМЕЖДУ приложения Excel).

Такие таблицы можно сохранить для последующего использования в процессе имитационных прогонов, но с точки зрения использования компьютерной памяти это неэффективно.

Общепринятым на сегодняшний день можно считать подход, при котором очередное случайное число всякий раз, когда возникает в нем необходимость, генерируется специальными программами.

Вопрос 2. Моделирование изменчивости с помощью случайных чисел.

Случайные числа из Табл. 6 можно использовать для назначения типа поступающему требованию так, что 60% случайных чисел будут соответствовать запросу типа 1 и 40% - запросу типа 2. Для этого значениям случайного числа в диапазоне 00-59 следует поставить в соответствие заявки типа 1, а значениям случайного числа в диапазоне 60-99 - заявки типа 2 (Табл. 7).

Таблица 7.

Случайные числа	Тип клиента
00-59	1
60-99	2

Например, если просматривать таблицу по столбцам начиная с самого верхнего элемента левого столбца, то первый пришедший клиент (65) будет отнесен к клиентам типа 2, второй, третий, четвертый, пятый и шестой клиенты (значения случайного числа равны соответственно 56, 10, 51, 55, 32) - к типу 1, седьмой, восьмой, девятый (68, 93, 94) - к типу 2 и т.д. Очевидно, что соотношение числа клиентов типа 1 и числа клиентов типа 2 будет все более приближаться к соотношению 60:40 по мере роста числа пришедших клиентов.

Воспользовавшись тем же примером центра обслуживания, будем теперь предполагать, что запросы поступают не через фиксированные интервалы времени, а через интервалы, продолжительность которых различна, что больше соответствует реальной ситуации.

На Рис. 11 показано распределение числа наблюдавшихся интервалов между приходами клиентов в зависимости от длительности временного интервала.

Рис. 11. Распределение частот величин интервала между приходами клиентов

Средним значением этого распределения является величина в 3 минуты, но реально наблюдавшийся диапазон определяется границами от нуля (клиенты приходят одновременно друг с другом) до 7 минут.

По аналогии с тем, как случайные числа используется для определения типа прибывшего клиента, случайные числа можно теперь использовать для определения величины интервала, связав их с частотами, показанными на Рис. 11.

Для этого предварительно нужно предварительно подготовить Табл. 8, включающую кумулятивные значения частот:

Таблица 8.

Случайные числа	Интервал между заявками, мин
00-13	0-1
14-37	1-2
38-67	2-3
68-85	3-4
86-94	4-5
95-98	5-6
99	6-7

Соответствующая гистограмма показана на Рис. 12.

Рис. 12. Гистограмма интегрального распределения интервалов

По аналогии со способом розыгрыша типа вызова, который был рассмотрен выше, для определения величины интервала между приходом вызовов можно также использовать случайные числа.

Однако в данном случае этот способ позволит нам получить не точное значение величины, а только диапазон, в который попадает величина интервала. С целью получить фактическое значение временного промежутка нужно использовать еще одно случайное число, поделить его на 100 и добавить результат деления к нижней границе диапазона. В Табл. 9 приведен пример получения значений интервала времени между приходами десяти клиентов для распределения интервалов, задаваемого Рис. 12.

Таблица 9.

Клиент	Первое случайное число	Интервал между приходами	Второе случайное число	Значение интервала
1	68	3-4	03	3,30
2	45	2-3	98	2,98
3	57	2-3	96	2,96
4	39	2-3	18	2,18
5	65	2-3	92	2,92
6	89	4-5	46	4,46
7	47	2-3	45	2,45
8	06	0-1	82	0,82
9	59	2-3	14	2,14
10	79	3-4	55	3,55

В качестве значений первого случайного числа в таблице используются значения седьмой строки Табл. 6, в качестве значений второго случайного числа- значения шестнадцатой строки. Разные строки взяты с целью обеспечения большей независимости выборок.

Можно заметить, что средним значением интервала между приходами клиентов является величина 2,78 (с точностью до второго знака после запятой), которое значительно отличается от среднего, получаемого по всему распределению (равного 7, как указывалось выше). Тот же вывод можно сделать относительно частот появления интервалов – они отличаются от частот, показанных на Рис. 11.

Очевидно, что эти различия будут становиться тем менее заметными, чем больше число значений интервалов будет получаться с помощью описанного метода.

С тем, чтобы проводить имитацию работы реальной системы, нужно проследить протекание процесса на довольно большом временном интервале. Следовательно, провести имитацию прихода клиентов многократно. Для того, чтобы получать значения интервалов между приходами, можно использовать те же значения случайных чисел, в данном случае, числе из строк 7 и 16 Табл. 6.

Однако более правильным будет использовать случайные числа из других строк, поскольку это обеспечит независимость получаемых значений друг от друга. Поэтому для практических применений важным является количество имеющихся в распоряжении аналитика (разработчика модели) случайных чисел. Чем больше будет массив этих чисел, тем более достоверными можно считать получаемые в результате моделирования результаты.

Вопрос 3. Выборки из теоретических распределений.

Рассмотренные выше приемы основывались на использовании данных, которые были получены опытным путем (как результат проведенных наблюдений). Наряду с этим на практике может возникнуть необходимость в получении значений чисел, которые подчиняются определенному закону распределения, например, нормальному. Подход в этом случае аналогичен по своей сути уже описанному подходу.

Рассмотрим для примера нормальное распределение с математическим ожиданием m, или средним равным 5 и среднеквадратическим отклонением σ равным 1. График функции плотности распределения f(x) нормального распределения показан на Рис. 13.

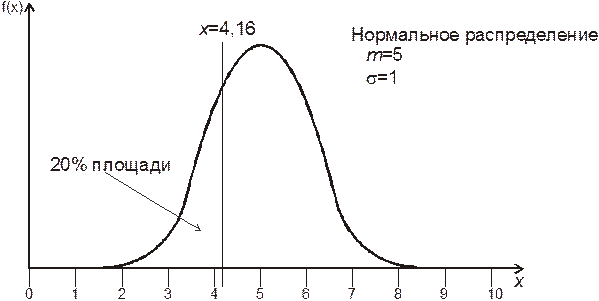
Рис. 13. График функции плотности нормального распределения

Непрерывная случайная величина t имеет нормальное, или гауссово распределение вероятностей с параметрами m>0 и σ>0, если ее плотность вероятностей имеет вид

где

т - математическое ожидание ;

σ - среднеквадратичное отклонение.

График функции плотности этого распределения симметричен относительно математического ожидания.

Нормальное, распределение является одним из наиболее важных и часто используемых в практике имитации деловых процессов видов непрерывных распределений. Чтобы пояснить возможные ситуации, когда возникает необходимость в применении этого вида распределения, рассмотрим Рис. 14.

Рис. 14. Механизм появления нормального распределения

Временная диаграмма рисунка означает, что какой-то случайный процесс состоит из последовательности n элементарных независимых работ (независимость в данном случае означает, что длительность выполнения какой-либо работы не зависит от длительности выполнения других). Длительность каждой работы есть случайная величина, распределенная по неизвестному закону с математическим ожиданием и дисперсией .

Если допустить, что это распределение непрерывно (что вполне оправдано для нормальных условий протекания деловых процессов) и третий момент ограничен по абсолютной величине (что также вполне реально), то для математического ожидания и дисперсии суммарной продолжительности (случайной величины) будут справедливы соотношения:

Иначе говоря, любые сложные по своему составу работы, выполняемые на объекте экономики (ввод информации из документа в компьютер, проведение переговоров, ремонт оборудования и т.п.), состоят из множества относительно коротких выполняемых последовательно одна за другой элементарных работ. Причем количество этих работ иногда велико настолько, что требования независимости и одинаковом распределении не нуждаются в специальной проверке. Поэтому при оценках трудозатрат всегда справедливо предположение о том, что продолжительность работ есть случайная величина, распределенная по нормальному закону.

Чтобы произвести выборку значения случайного числа, распределенного по такому закону, нужно, чтобы число выбираемых значений случайного числа x было пропорционально площади, лежащей под кривой графика функции плотности распределения. Если, к примеру, случайное число из равномерного распределения от 0 до 100 равно 20, то значением выборки должно быть такое число x, чтобы площадь под кривой графика функции составляла от общей площади (под всем графиком) 20%. В данном примере значением x, которое обеспечивает выполнение этого равенства, является число 4,16.

Однако поиск выборочного значения x по такому правилу весьма неудобен. Поэтому на практике вместо функции распределения плотности вероятности используется интегральная функция распределения (или просто функция распределения) F(x). Для данного примера график функции распределения показан на Рис. 15.

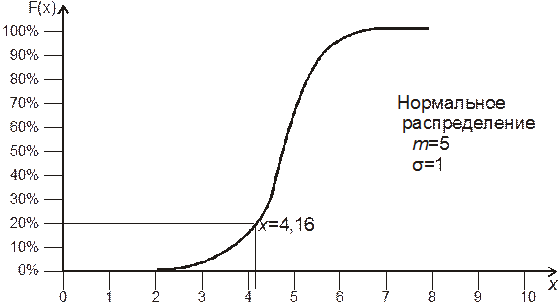
Рис. 15. График интегральной функции нормального распределения

Найдя нужную точку на оси F(x), например, 20, можно определить выборочное значение x.

Рассмотренный подход известен под названием метода обратной функции. Несмотря на то, что принцип, на котором он построен, отличается простотой и очевидностью, его практическая реализация может столкнуться с рядом проблем, вызванных сложностью нахождения величины x из математического уравнения, которое не обязательно имеет точное решение. Однако в современных пакетах прикладных программ и системах имитационного моделирования присутствуют специальные средства, в основу построения которых положены специальные методы, позволяющие преодолеть эту проблему.

Вопрос 4. Компьютерная генерация псевдослучайных чисел.

Для проведения имитационных экспериментов на моделях среднего и крупного размера требуется порядка сотен тысяч и миллионов случайных чисел. Как уже отмечалось, применять для этого заранее заготовленные таблицы типа описанных выше с практической точки зрения оказывается нецелесообразным – необходимо затратить значительное время на подготовку самих значений и зарезервировать большой объем памяти компьютера для хранения чисел во время выполнения программы. По этой причине обычным способом получения очередного значения случайного числа является их программная генерация.

Все компоненты компьютера представляют собой детерминированные блоки и устройства, иначе говоря, результат работы их является полностью предсказуемым. Следовательно, они не могут служить источником какой-либо случайности.

Поэтому в качестве средства получить требуемые значения используются алгоритмы, результатом выполнения которых являются псевдослучайные числа. Это название означает, что, несмотря на детерминированный характер их происхождения и полную предсказуемость очередного получаемого значения, числа обладают всеми свойствами, которые позволяют с точки зрения требований к условиям проведения имитационных экспериментов, рассматривать их как случайные.

Одним из наиболее известных и распространенных алгоритмов генерации случайных чисел является алгоритм Лемера, известный также как метод линейного конгруента. Алгоритм основан на применении рекуррентного выражения, которое использует только одну операцию умножения (длинную операцию), поэтому является с вычислительной точки зрения достаточно эффективным:

Для генерации последовательности псевдослучайных чисел {Xn} используется алгоритм, основанный на применении итерационного равенства

параметры которого имеют следующий смысл:

m - Модуль (основание системы), m > 0;

a - Множитель, 0 ≤ a < m;

c - Приращение, 0 ≤ с < m;

- Начальное значение, или зерно (seed), 0 ≤ < m.

Если m, а и с являются целыми числами, то создается последовательность целых чисел в диапазоне 0 ≤ < m.

Для хорошего генератора случайных чисел выбор значений а, с и m является важным. Существует три критерия, используемые при выборе генератора случайных чисел:

· функция должна создавать полный период, т.е., должны появиться все числа между 0 и m до того, как создаваемые числа начнут повторяться;

· создаваемая последовательность должна появляться случайно. фактически последовательность чисел не является случайной, так как она создается детерминированным образом, но различные статистические тесты, которые могут применяться, должны показывать, что последовательность случайна;

· программа, реализующая метод, должна эффективно выполняться на 32-битных процессорах.

Значения а, с и m должны быть выбраны таким образом, чтобы эти три критерия выполнялись. Можно показать, что если m является простым и с = 0, то при определенном значении а период, создаваемый функцией, будет равен m-Для 32-х битной арифметики соответствующее простое значение m = 231 - 1. Таким образом, функция создания псевдослучайных чисел имеет вид:

Только небольшое число значений а удовлетворяет всем трем критериям. Одно из таких значений а = 75 = 16807, которое использовалось в семействе компьютеров IBM 360.

Генератор широко применяется, и подвергался проверке более чем на тысяче различных тестов (больше, чем все другие генераторы псевдослучайных чисел).

В Табл. 10 приведены первые 45 значений псевдослучайного числа, сгенерированные конгруентным алгоритмом.

Таблица 10.

Для задания базового значения в программе использовано битовое содержимое таймера компьютера, что обеспечивает случайных характер выбора начальной точки последовательности чисел. Это удобно для проведения экспериментов на модели, но создает сложности в процессе ее отладки, так как не дает возможность обеспечить воспроизводимость запусков. С целью обойти эту проблему следует задавать в качестве начального значения конкретную величину, одну и ту же для всех отладочных тестов.

Однако такие особенности распределения случайных чисел, генерируемых линейным конгруэнтным алгоритмом как период псевдослучайной последовательности и неравнозначность битов получаемого случайного числа по статистическим свойствам, затрудняют и даже делают невозможным использование таких генераторов в задачах, требующих повышенной точности генераторов случайных числовых последовательностей. Такими задачами, в частности, являются:

· исследование влияния рисковых событий в процессе имитации хозяйственно-экономической, финансовой, военной или иной деятельности, для которой эти события представляют угрозу;

· изучение длинных «хвостов» распределений вероятностей рисковых событий в деловых процессах для задач прогнозирования.

В указанных задачах наряду с модификациями конгруэнтных алгоритмов в настоящее время начинают применяться и другие алгоритмы (в частности, алгоритмы, получившие название фибоначчиевых). Несмотря на сложность их программной реализации, такие алгоритмы можно рекомендовать в качестве инструментария проведения исследований, критичных к качеству случайных чисел.

Выводы:

1. Стохастическая природа экономические процессов требует для их моделировании специальных методов, обеспечивающих имитацию случайного характера их протекания. Все методы основаны на использовании случайных чисел.

2. Для получения очередного значения случайной величины могут использоваться как результаты проведенных наблюдений, так и вероятностное описание в аналитическом виде. В первом случае производятся выборки из таблиц частот наблюдавшихся значений, во втором случае применяется математическое выражение для функции теоретического распределения.

3. Одним из наиболее часто встречающихся на практике видов распределения случайных величин, характерных для экономических процессов, является нормальное распределение. Распределение наблюдаемой или вычисляемой случайной величины можно считать нормальным после проверки соблюдения нескольких обязательных в этом случае ее свойств.

4. Использование в процессе имитации заранее сформированных массивов случайных чисел неэффективно, поскольку приводит к перерасходу ресурсов компьютера, поэтому для получения случайных чисел на практике применяются специальные программы-генераторы псевдослучайных чисел. Одним из наиболее распространенных алгоритмов, применяемых в этих программах, является алгоритм Лемера. Этот алгоритм приемлем для большинства реальных ситуаций, но в некоторых задачах необходимо применять более сложные методы.

Вопросы для самопроверки:

1. Чем объясняется важность задачи моделирования непредсказуемых изменений?

2. Как могла бы выглядеть физическая модель имитации типа пришедшего в систему клиента (заявки)?

3. Что представляют собой случайные числа?

4. Какими важными свойствами должны обладать случайные числа, используемые для имитации значения фактора с изменяющимся значением?

5. Какими средствами (источниками) можно воспользоваться для получения значений случайных чисел?

6. Какой метод получения случайных чисел обычно используется в современных программных системах имитации?

7. Как можно использовать случайные числа для определения временных параметров (поясните на примере определения величины интервала между приходами клиентов)?

8. Каким образом будет вести себя значение среднего интервала между приходами клиентов по мере роста числа пришедших клиентов?

9. Какие параметры, и каких реально происходящих процессов могут описываться нормальным законом распределения вероятностей?

10. Какие условия должны выполняться для того, чтобы некоторый параметр реального процесса можно было считать распределенным по нормальному закону?

11. Что может служить указанием на возможность отнесения распределения некоего параметра процесса к нормальному?

12. Что является основным способом получения случайных чисел в процессе компьютерной имитации процессов?

13. Как называются числа, получаемые программным путем и используемые в качестве случайных чисел, и почему?

14. Какое выражение лежит в основе алгоритма Лемера?

15. Как формулируются критерии, предъявляемые к генераторам случайных чисел?

16. Каким следует задать начальное значение генератора псевдослучайных чисел для отладочных запусков модели?

17. Какое начальное значение генератора псевдослучайных чисел обычно устанавливается для имитационных прогонов?

18. Для решения каких задач требуется повышенная точность генератора случайных числовых последовательностей?

Литература по теме:

Основная литература:

Дополнительная литература:

1. Н.Н. Снетков Имитационное моделирование экономических процессов. Учебно-практическое пособие – М.: Изд. центр ЕАОИ, 2008. – 228 с.

2. Шенон Р. Имитационное моделирование систем - искусство и наука. – М.: Мир, 1978 – 424 с.

Практические задания:

Выполните задание Темы 3, изменив постановку задачи следующим образом.

1. Время занятости взлетно-посадочной полосы не является постоянным для всех воздушных судов, а зависит от типа воздушного судна: для тяжелых воздушных судов, доля которых равна 30%, это время составляет 2,5 минуты, а для легких – 1,5 минуты.

2. После получения разрешения на посадку до начала ее выполнения проходит время, определяемое как случайная величина, равномерно распределенная в интервале от 0 до 1минуты.

3. Для прилетающих воздушных судов задаются не моменты прилетов, а интервалы между прилетами, которые являются случайными величинами. Диапазоны и частоты значений для интервалов задаются следующей таблицей частот:

Интервал (мин)	Доля
2-3	30%
3-4	40%
4-5	25%
5-6	5%

Тема 5. Инструментальные средства имитации

Цели изучения темы:

· изучить возможности современных программных систем компьютерной имитации.

Задачи изучения темы:

· познакомиться с историей возникновения и развития программных систем компьютерной имитации;

· познакомиться с основными функциональными возможностями современных программных систем компьютерной имитации.

Успешно изучив тему, Вы:

Получите представление о:

· специфике создания модели с помощью графического интерфейса разработчика с программной системой имитационного моделирования;

· последовательности и характере действий, выполняемых в процессе создания модели;

· возможном порядке выполнения имитационных прогонов.

Будете знать:

· что представляет собой описание модели в системе имитационного моделирования Pilgrim;

· что и как необходимо сделать для получения программной модели;

· из чего состоят и в какой форме представляются результаты имитационных прогонов;

· что такое простейший поток, и каким образом можно использовать экспоненциальное распределение в имитационных моделях экономических процессов.

Вопросы темы:

1. Краткий исторический очерк.

2. Типы программных систем имитации.

3. Применение современных технологий имитационного моделирования.

4. Замкнутые имитационные модели.

Вопрос 1. Краткий исторический очерк.

Первые имитационные эксперименты с помощью вычислительной техники стали проводиться, начиная с 50-х годов прошлого века. Программы для имитационного моделирования, как и все программы, создаваемые в этот период, разрабатывались в машинных кодах. В конце 50-х годов появились первые трансляторы с алгоритмических языков, таких как FORTRAN (FORmula TRANslator), которые стали применяться также и для имитационного моделирования. Появление первых специализированных языков для имитационного моделирования относится к концу 60-х годов, были созданы такие языки как SIMULA (SIMUlation LAnguage), GPSS (General Purpose Simulation System) и ряд других. Большое распространение в нашей стране получил разработанный в киевском институте кибернетики язык моделирования СЛЭНГ.

Для изучения экономических процессов метод их имитации в этот период впервые применил Т. Нейлор. Однако из-за сложности формализации деловых процессов на протяжении примерно двух десятилетий большого развития имитационное моделирование для решения задач экономики не находило. Сложность была обусловлена двумя обстоятельствами.

Во-первых, в математическом обеспечении ЭВМ не было формальной языковой поддержки описания элементарных процессов и их функций в узлах сложной стохастической сети экономических процессов с учетом их иерархической структуры.

Во-вторых, отсутствовали формализованные методы структурного системного анализа, необходимые для иерархического (многослойного) разложения (декомпозиции) реального моделируемого процесса на элементарные составляющие.

Одной из наиболее развитых систем, появившихся в этот период, является система SLAM-II, позволяющая создавать сложные модели дискретно-непрерывных процессов. Методология, заложенная в систему SLAM-II, резко расширила область применения имитационного моделирования. Однако система имеет некоторые недостатки: она сложнее GPSS-V в освоении неподготовленным пользователем, в ней нет собственных средств имитации пространственных процессов.

Следующим этапом развития технологии имитации было появление программных средств, содержавших возможности визуализации имитируемых процессов и графический интерфейс пользователя, которые облегчали решение задачи интерпретации результатов имитационных экспериментов и делали более простой и эффективной работу по созданию программной модели. Импульсом для создания этих программ стало бурное развитие микропроцессорной техники и появление персональных компьютеров.

Из наиболее известных систем, появившихся в этот период, можно отметить:

· Process Charter-1.0.2 (имеет «интеллектуальное» средство построения блок-схем моделей, ориентирован, в основном, на дискретно-событийное моделирование).

· Powersim-2.01 (обеспечивает создание непрерывных моделей).

· Ithink-3.0.61 (обеспечивает создание непрерывных и дискретных моделей).

· Extend+BPR-3.1 (BPR - Business Process Reengineering, средство анализа деловых процессов, использовался в NASA, поддерживает дискретное и непрерывное моделирование).

· ARENA (разработка Systems Modeling, права с 2000 года у Rockwell Automation, использует графический интерфейс пользователя, имеет встроенный язык VBA, возможности чтения и интерпретации диаграмм MS Visio, информационный интерфейс с MS Excel и MS Access, что позволяет легко интегрировать модель в технологии Microsoft).

В настоящее время доступными для использования являются многие программные системы имитационного моделирования. Чтобы осуществлять осознанный выбор из всего имеющегося многообразия разработчик модели должен иметь представление об основных возможностях систем.

Вопрос 2. Типы программных систем имитации.

Принципиально возможно использовать три типа программ для организации имитационных экспериментов.

Электронные таблицы.

Для создания простейших моделей ряд возможностей предоставляют программы типа Excel, реализующие работы с электронными таблицами. В частности, в пакете Excel присутствуют средства генерации псевдослучайного числа (СЛЧИС, СЛУЧМЕЖДУ), для выборки значений из таблиц с распределениями частот можно использовать такие функции как ЕСЛИ, ПРОСМОТР, ПОИСКПОЗ (для некоторых частных распределений функции для выборки значений случайной величины присутствуют в явном виде), есть довольно много статистических функций.

Однако даже для простейших моделей, скорее всего, понадобится использовать какие-либо средства автоматизации в виде макросов или встроенного в пакет языка Visual Basic for Applications.

Универсальные языки программирования.

Имитационные модели можно создавать с использованием языков программирования, Таких как Visual Basic, C++ и Java. Это позволяет разработчику в создаваемой модели практически полностью реализовать все требуемые особенности. Однако такой вариант характерен большими временными затратами как на создание модели, так и на внесение в нее изменений, поскольку потребуется воссоздавать весь механизм имитации процессов (как это рассматривалось ранее). Кроме того, это повышает требования к квалификации разработчика (он должен уметь хорошо программировать) и усложняет процесс взаимодействия между участниками проекта.

Специализированные системы имитационного моделирования.

Специализированные средства имитационного моделирования представляют собой наиболее мощные программные комплексы, предоставляющими конечному пользователю богатый арсенал разнообразных средств для проведения работ как по созданию и обоснованию моделей, так и проведению с их помощью имитационных экспериментов. В конце 1990-х гг. в России разработаны такие системы как:

· РДО (Ресурсы-Действия-Операции, МГТУ им. Н.Э. Баумана, мощная система для создания продукционных моделей, обладает развитыми средствами компьютерной графики и анимации, применяется при моделировании сложных технологий и производств).

· СИМПАС (Система-Моделирования-на-ПАСкале, МГТУ им. Н.Э. Баумана, в качестве основного инструментального средства использует язык Паскаль, предназначен для моделирования информационных процессов, компьютеров сложной архитектуры и компьютерных сетей).

· Anylogic (Экс Джей Текнолоджис, объединяет возможности моделей системной динамики, методов дискретно-событийного и агентного моделирования, обладает развитыми средствами анимации).

· Pilgrim (МЭСИ и ряд компаний).

Все перечисленные средства имеют графический интерфейс для конструирования модели - на одной графической схеме моделируемые процессы можно связывать с управленческими процессами и включать в модель конструктивные особенности моделируемой системы.

Кроме того, многие современные пакеты имитационного моделирования обладают средствами визуально-интерактивной имитации.

Идея, которая лежит в основе систем моделирования, обеспечивающих визуально-интерактивную имитацию, состоит в анимации поведения элементов модели в процессе имитационного эксперимента. Такими элементами могут быть, в частности, клиенты, диспетчер и операторы центра технического обслуживания, отдельные транспортные средства в модели, имитирующей транспортные потоки, документы в модели документооборота и т.п.

Для отображения состояния отдельных элементов модели на мониторе могут использоваться разные цвета (например, зеленый, желтый и красный для обозначения рабочего состояния, состояния простоя и состояния неисправности какого-либо устройства). Степень подробности и качество анимации могут варьироваться в очень широких пределах от простого, схематичного представления процессов до трехмерной графики.

Пользователь в условиях работы по данной технологии получает возможность вмешиваться в ход имитации. Он может, в частности, остановить работу программы с тем, чтобы внимательно изучить состояние процесса, получив подробную информацию о значениях показателей функционирования изучаемой системы, и изменить течение процесса, установив другие значения управляемых параметров. Например, в модели работы центра технического обслуживания можно добавить дополнительного оператора, если выясняется, что очередь к операторам начинает расти.

Остановку работы программной модели можно производить и запланировано, задавая точки останова по времени или по условию.

В дополнение к описанным возможностям для имитационного моделирования разработан целый ряд других усовершенствований, которые значительно облегчают работу конечных пользователей и повышают эффективность работы по созданию и применению модели. Эти усовершенствования могут применяться на всех этапах жизненного цикла моделирования, начиная с этапа определения и включая этапы обоснования модели, конфигурирования модели в системе принятия решений вплоть до этапа работы с моделью в оперативном режиме и внесения в нее модификаций.

В итоге рассмотрения функциональных возможностей современных программных средств имитации можно заключить, что технология визуально-интерактивных моделей:

· помогает более глубоко понять как саму модель, так и упростить интерпретацию результатов моделирования;

· упрощает процесс проверки модели и обоснования адекватности;

· дает возможность проведения имитационных экспериментов в интерактивном режиме;

· облегчает процесс взаимодействия разработчика и/или экспериментатора с моделью;

· способствует коллективной работе с моделью.

Вопрос 3. Применение современных технологий имитационного моделирования.

Покажем на примере уже рассматривавшейся ранее модели системы технического обслуживания, со структурой на Рис. 8 и включающей двух операторов, как с помощью графического интерфейса можно создать программную модель для проведения имитационных экспериментов и использовать ее для имитационных экспериментов. В качестве инструментальной системы будем использовать систему имитационного моделирования Pilgrim.

Все модели в системе Pilgrim представляются графом, который образован узлами, представляющими собой центры обслуживания запросов на обслуживание. Запросы на обслуживание носят название транзактов и имеют ряд параметров, идентифицирующих транзакт и его текущее состояние.

Для построения модели в системе Pilgrim применяется графический конструктор моделей, который называется Gem и имеет интерфейс в стиле Windows. Основное окно включает, в частности, строку меню, строку клавиш быстрого вызова, панель инструментов и рабочую плоскость для построения графа модели:

Все узлы имеют для своего обозначения графические символы с надписью, поясняющей функцию узла, расположенной внутри символа. Для построения графа модели системы технического обслуживания понадобятся следующие узлы.

· ag: генератор транзактов имитационной модели;

· queue (q): очередь транзактов;

· serv (s): сервер (обслуживающий прибор);

· term (t): терминатор (уничтожитель транзактов).

Узел графа на рабочей плоскости создается перетаскиванием изображения узла при нажатой левой кнопке мыши.

Узлы нумеруются автоматически (первая цифра номера означает номер плоскости, так как в системе Pilgrim есть возможность построения иерархического графа моделей).

Имена узлов вместе с прочими их параметрами указываются в диалоговых окнах свойств узлов, вход в которые осуществляется с помощью двойного щелчка мыши на изображении узла графа.

После перетаскивания изображений нужных для модели технического обслуживания узлов на рабочую плоскость и соединения узлов дугами, показывающими возможные маршруты перемещения транзактов, получим граф:

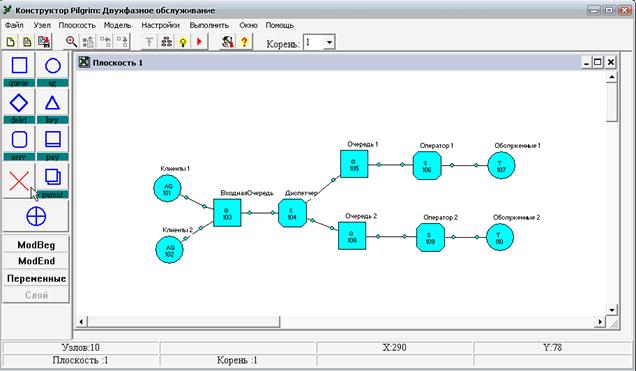
Узлы «Клиенты 1» и «Клиенты 2» осуществляют генерацию транзактов согласно характеристикам потоков клиентов типа 1 и типа 2, приходящих в центр обслуживания.

Узлы «ВходнаяОчередь», «Очередь 1» и «Очередь 2» имитируют ожидания клиентов в очередях к диспетчеру и операторам.

Узлы «Диспетчер», «Оператор 1» и « Оператор 2» имитируют процессы обслуживания клиентов диспетчером, первым и вторым оператором соответственно.

Узлы «Обслуженные 1» и « Обслуженные 2» удаляют из модели транзакты, имитирующие клиентов, обслуживание которых закончено (это обеспечивает освобождение участков памяти компьютера, выделенных для хранения сведений о транзакте).

Сначала задаем свойства генераторов транзактов с помощью окон свойств:

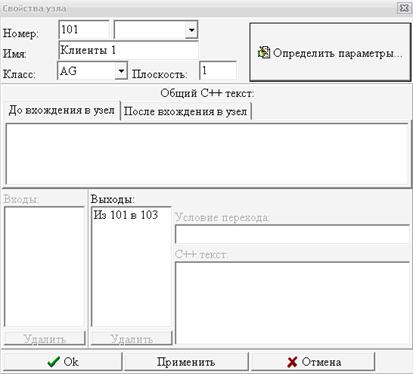
Для каждого узла ag нужно определить закон распределения величины временного интервала между сгенерированными транзактами вместе с его параметрами и значения их приоритета. Для этого используется окно, открываемое нажатием кнопки «Определить параметры»:

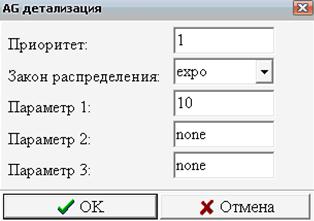
Это означает, что в качестве закона распределения интервала между приходами задан экспоненциальный закон со средним временем 10.

Установим теперь значения параметров для второго генератора транзактов:

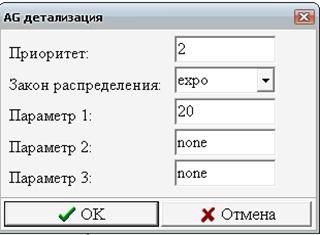
Клиентам типа 2, как видно из окон задания параметров, назначен больший приоритет по отношению к клиентам типа 1 (2 и 1 соответственно). В данном случае значения приоритетов выбраны разными для удобства распознавания типа клиентов (транзактов). Но на самом деле приоритет может использоваться для изменения порядка формирования очереди или дисциплины обслуживания.

Далее задаем свойства узла «ВходнаяОчередь»

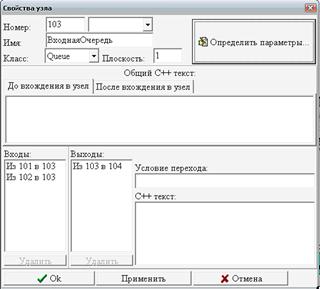
и узла «Диспетчер»

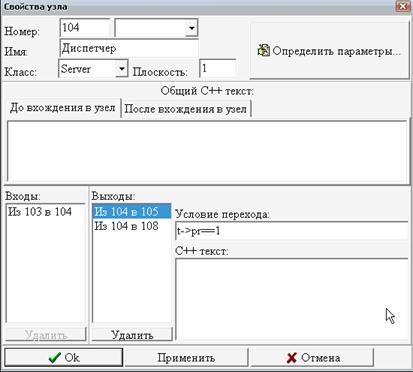
В окне свойств последнего узла задается правило, определяющее направление дальнейшего следования транзактов. В нашей модели транзакты, имитирующие клиентов типа 1, должны, покинув узел serv, идти в узел «Очередь 1». Правило задается как:

· указание узла с номером 105 в качестве приемника транзактов (блок Выходы), имеющих приоритет равный 1 (условие t->pr==1 в блоке Условие перехода);

· указание узла с номером 108 в качестве приемника транзактов (блок Выходы), имеющих приоритет равный 2 (условие t->pr==2 в блоке Условие перехода).

Для узла «Диспетчер» задаются число каналов (1, работает один диспетчер), режим работы с абсолютными приоритетами (none – более высокоприоритетные клиенты обслуживание низкоприоритетного не прерывают), закон распределения (norm – нормальный) времени обслуживания клиентов диспетчером, его среднее значение (2 минуты) и среднеквадратическое отклонение (2/3 минуты):

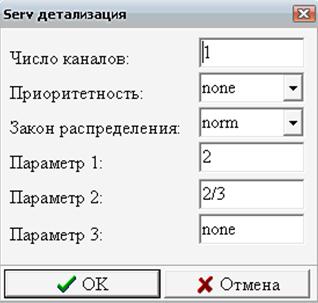
Аналогичным образом описываются свойства и параметры узлов «Очередь 1» и «Очередь 2» (показано окно для первого из этих узлов)

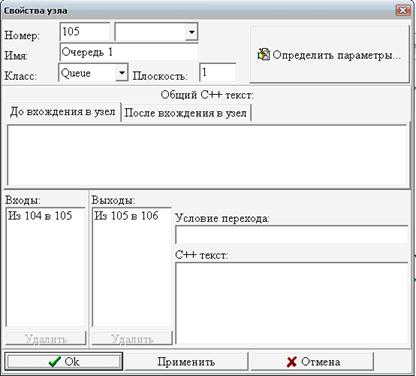
«Оператор 1» и « Оператор 2» (показаны окно свойств и окно параметров для первого из этих узлов, для среднего и среднеквадратического отклонения времени обслуживания второго оператора устанавливаются значения 16 и 16/3 соответственно)

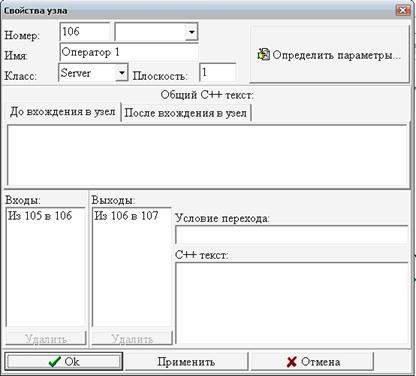
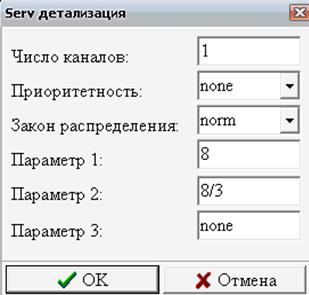
Для узлов-терминаторов задаются только имена (показан первый из узлов)

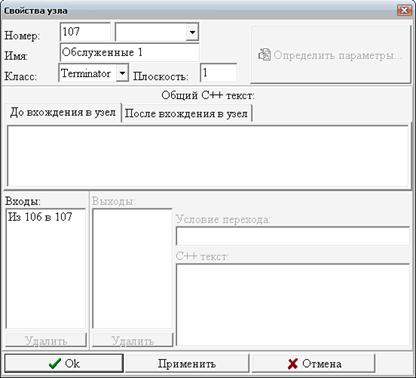
Теперь необходимо задать параметры запуска (инструмент modbeg)

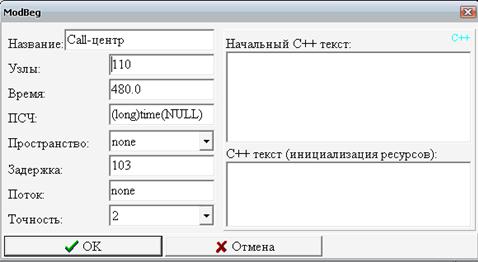
Здесь можно видеть, что для времени моделирования (Время) выбрана продолжительность в 480 минут (рабочий день) и в качестве начального значения последовательности псевдослучайных чисел (ПСЧ) используется текущее содержимое компьютерного таймера - (long)time(null). Для узла 103 (Задержка) можно будет отобразить график среднего времени ожидания транзактов в этом узле (очереди).

Последнее необходимое действие по созданию описания модели состоит в указании параметров файла с результатами имитационного прогона (инструмент modend панели инструментов).

После выполнения команды Сгенерировать С++ файл меню Выполнить

конструктор создаст файл с исходным текстом на языке С++:

#include <Pilgrim.h>

forward

{

int fw;

modbeg("Call-центр", 111, 480.0, (long)time(NULL), none, 103, none, none, 2);

ag("Клиенты 1", 101, 1, expo, 10, none, none, 103);

ag("Клиенты 2", 102, 2, expo, 20, none, none, 103);

network(dummy, dummy)

{

top(103):

queue("ВходнаяОчередь", none, 104);

place;

top(104):

if( t-> pr == 1 ) fw=105; else fw=108;

serv("Диспетчер", 1, none, norm, 2, 2/3, none, fw);

place;

top(105):

queue("Очередь 1", none, 106);

place;

top(106):

serv("Оператор 1", 1, none, norm, 8, 8/3, none, 107);

place;

top(107):

term("Обслуженные 1");

place;

top(108):

queue("Очередь 2", none, 109);

place;

top(109):

serv("Оператор 2", 1, none, norm, 14, 14/3, none, 110);

place;

top(110):

term("Обслуженные 2");

place;

fault(123);

}

modend("CallCenter.txt", 1, 8, page);

return 0;

}

Хотя знание структуры и форматов С++-модуля не является строго обязательным, умение ориентироваться в исходном тексте могут в ряде случаев ускорить дальнейшую работу с моделью и проведению экспериментов. Познакомиться с подробным описанием этих аспектов можно в [1].

Вслед за этим по обычным правилам нужно создать проект С++, после чего можно выполнить прогон получившегося исполнительного модуля.

В итоге прогона можно получить файл с его результатами

НАЗВАНИЕ МОДЕЛИ:			Call-центр
ВРЕМЯ МОДЕЛИРОВАНИЯ:			482.63									Лист: 1
								2
№ узла	Наименование узла	Тип узла		Точка	Загрузка (%=), Путь (км)	M [t] среднее время	C [t] квадрат коэф. вар.		Счетчик входов и hold	Кол. кан.	Оcт. тр.	Состояние узла в этот момент

101	Клиенты 1	ag		-	-	10.04	1.08		47	1	1	открыт
102	Клиенты 2	ag		-	-	16.72	1.57		29	1	1	открыт
103	Входная Очередь	queue		-	-	0.53	2.77		75	1	1	открыт
104	Диспетчер	serv		-	%= 30.7	2.00	0.00		74	1	0	открыт
105	Очередь 1	queue		-	-	7.93	1.00		46	1	0	открыт
106	Оператор 1	serv		-	%= 73.3	7.69	0.05		46	1	0	открыт
107	Обслуженные 1	term		-	-	18.24	0.21		46	0	0	открыт
108	Очередь 2	queue		-	-	15.26	0.45		28	1	3	открыт
109	Оператор 2	serv		-	%= 73.4	14.77	0.06		25	1	1	закрыт
110	Обслуженные 2	term		-	-	32.00	0.12		24	0	0	открыт

и график зависимости задержки в очереди диспетчера от времени моделирования

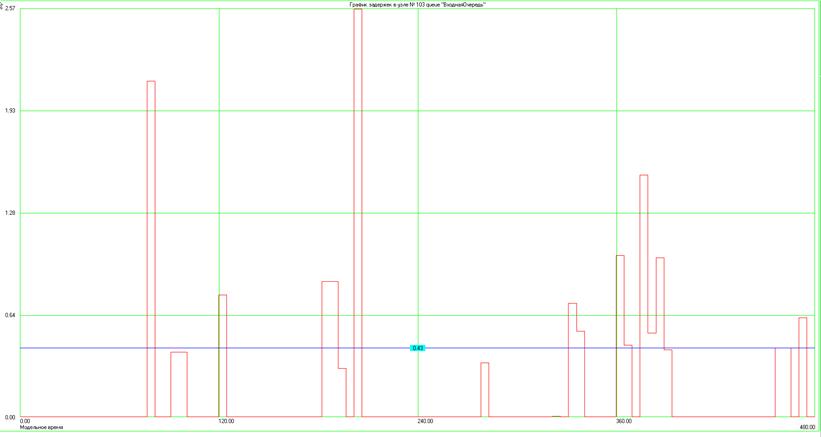
Файл с результатами моделирования имеет вид таблицы, строками которой являются узлы графа модели, а столбцами – значения параметров узлов. При беглом знакомстве с результатами имитации можно заметить, что в то время, как загрузка диспетчера (узел Диспетчер) довольна мала (около 30%) и среднее время ожидания клиентами в его очереди совсем невелико (около полминуты), среднее время ожидания клиентами обслуживания операторами уже довольно ощутимо (7,93 минуты и 15,26 минуты соответственно).

График зависимости задержки в очереди строится путем деления всего времени моделирования на малые интервалы, вычисления среднего времени нахождения в очереди внутри каждого интервала и соединением отрезками прямых на графике. Горизонтальная линия синего цвета обозначает среднее время ожидания за весь интервал моделирования.

Изучение этого графика может быть полезным при проведении имитационных экспериментов в интерактивном режиме и при изучении не завершающихся моделей. С этими понятиями мы будем знакомиться во время изучения следующей темы.

Вопрос 4. Замкнутые имитационные модели.

Выше был рассмотрен случай, когда изучался внешний поток клиентов. При моделировании экономических процессов часто приходится сталкиваться с процессами, протекающими в так называемых замкнутых системах. Под замкнутой системой понимается система, в которой нет приходящих извне или уходящих наружу потоков. Примером такой системы может быть компьютерный класс – вышедшие из строя компьютеры поступают на ремонт в отдел технического обслуживания и после восстановления работоспособности возвращаются обратно.

Если формулировать это определение в терминах модели Pilgrim, то это значит, что транзакты, будучи раз сгенерированы, циркулируют в пределах графа модели, не погибая в терминаторах. В частности, если требуется смоделировать работу нескольких пользователей, выполняющих различную по своему характеру работу за своими терминалами (клиентскими компьютерами), то это может быть реализовано с помощью следующего графа (Рис. 16):

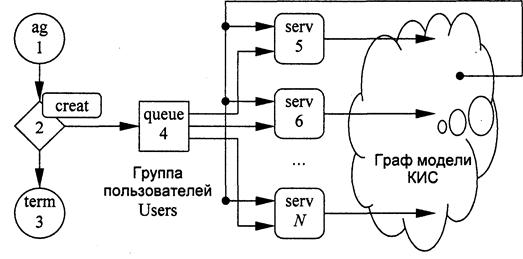
Рис. 16. Корпоративная информационная система

В этом случае модель может быть построена следующим образом:

· Пользователи (или группы пользователей, в зависимости от сложности моделируемой системы) представляются одно- или многоканальными узлами типа serv (серверы).

· Число каналов сервера соответствует числу пользователей, время обработки транзакта сервером соответствует времени подготовки пользователями запроса.

· Конкретное состояние транзакта (запрос – ответ) фиксируется значением одного из его параметров.

· Для зарядки транзактами серверов пользователей, принадлежащих к одному классу, используется единственный генератор, порождающий всего один транзакт. Далее транзакты размножаются с помощью узлов типа creat.

Значение среднего времени реакции на пользовательские запросы можно рассчитать на основании стандартного отчета с результатами моделирования системы Pilgrim. Для этого можно воспользоваться следующим выражением:

где

- означает среднее время обдумывания пользователем ответа системы перед выдачей ей нового очередного запроса.

Подробное описание работы такой схемы и обсуждение приемов получения значений выходных параметров содержится в [1].

Выводы:

1. Средства компьютерной имитации имеют более чем полувековую историю. В течение этого времени арсенал инструментальных средств моделирования прошел эволюцию от трансляторов с универсальных алгоритмических языков до сложных специализированных комплексов.

2. Для создания имитационных моделей и их применения для проведения экспериментов могут применяться различные средства различной степени функциональности. Выбор того или иного типа зависит, в первую очередь, от сложности решаемой задачи.

3. Одними из наиболее важных и востребованных возможностей современных систем имитационного моделирования являются графический интерфейс и визуально-интерактивная имитация. Наличие этих функций делает доступным использование инструментария прикладными специалистами и аналитиками, не имеющими специальной технической подготовки, значительно уменьшает время, необходимое для проведения экспериментов, и повышает надежность их результатов.

4. Несмотря на особенности, присущие конкретным системам моделирования, большинство из них строится на основе общих методологических принципов. Собственные стандарты, определяют, в первую очередь, правила взаимодействия пользователя с системой. Примером, наглядно демонстрирующим возможности современных подходов к построению моделирующих систем, является система Pilgrim.

5. В процессах, которые протекают на объектах экономики и которые можно охарактеризовать как обработку потоков заявок, случайные величины, обозначающие временные интервалы между поступающими заявками, во многих случаях подчиняются экспоненциальному распределению. Наряду с использованием его для имитации в компьютерных моделях это распределение дает возможность применить для получения нужных показателей процессов в ряде случаев аналитические модели, сократив тем самым время на получение результата.

Вопросы для самопроверки:

1. Какие этапы прошло развитие программных систем имитационного моделирования, и чем они были характерны?

2. Какие существуют типы программных систем имитации?

3. Для чего применяется графический интерфейс в системах имитационного моделирования?

4. Какая идея лежит в основе визуально-интерактивной имитации?

5. Какие возможности получает пользователь в случае применения технологии основе визуально-интерактивной имитации?

6. Какими преимуществами обладает технология визуально-интерактивной имитации?

7. Каким образом представляется модель в системе Pilgrim?

8. Какой компонент системы Pilgrim используется для создания модели?

9. Какие узлы следует использовать для графа модели центра обслуживания?

10. Что представляет собой экспоненциальный закон распределения?

11. Как выглядит математическая запись экспоненциального закона распределения?

12. Каким характерным свойством обладает экспоненциальный закон распределения?

13. Какие величины из встречающихся на практике могут описываться с помощью экспоненциального закона распределения?

14. Какой поток называется простейшим?

15. Каким образом можно задать режим приоритетного обслуживания в системе Pilgrim?

16. Каково назначение узла-терминатора?

17. Что представляют собой результаты имитационного прогона Pilgrim- модели и где они располагаются?

18. Какую структуру имеет выводной файл имитационного прогона?

19. Что собой представляет отображаемый график задержек в очереди?

20. В каких случаях возникает необходимость в получении графика задержек в очереди?

Литература по теме:

Основная литература:

Дополнительная литература:

1. Гусева Е.Н. Имитационное моделирование в среде Arena: [электронный ресурс] Учеб.метод.пособие – М.: ФЛИНТА, 2011 – 132 с.

2. Прицкер А. Введение в имитационное моделирование и язык СЛАМ II/пер. с англ. – М: Мир, 1987. – 646 с.

3. Шрайбер Т. Дж. Моделирование на GPSS – М.: Машиностроение, 1980 – 592 с.

4. Ю. Г. Карпов Имитационное моделирование систем. Введение в моделирование с AnyLogic 5 – С.Пб.: БХВ-Петербург, 2005 – 400 с.

Практические задания:

1. Для выполнения задания следует пользоваться указанным выше литературным источником.

С помощью конструктора Gem системы Pilgrim создайте граф модели процесса взлетов и посадок согласно описанию, приведенному в Теме 3.

Положите, что моменты прилетов и вылетов задаются не таблицами с их значениями, а временными интервалами между смежными прилетами и вылетами. Интервалы представляют собой случайные величины, распределенные по нормальному закону со средними значениями равными четырем минутам (как между смежными взлетами, так и между смежными посадками) со среднеквадратичными отклонениями равными 80 секундам.

Время, как взлета, так и посадки есть постоянная величина равная двум минутам.

Сгенерируйте модуль на исходном языке С++, соберите проект, проведите запуски и проанализируйте результаты.

2. Измените условие, положив, что поток прилетающих воздушных судов состоит на 30% из тяжелых воздушных судов и на 70% – из легких. Для тяжелых воздушных судов среднее величина времени посадки составляет 2,5 минуты со среднеквадратичным отклонением равным 50 секундам, а для легких – соответствующие величины равны 1,5 минуты и 30 секундам.

Тема 6. Тактическое планирование имитационных экспериментов

Цели изучения темы:

· понять сущность задачи правильной организации имитационных экспериментов и изучить основные методы ее решения.

Задачи изучения темы:

· выяснить возможные типы имитируемых процессов;

· понять необходимость тщательного анализа и создания необходимых условий проведения отдельных экспериментов;

· познакомиться с основными методами организации сбора и обработки данных имитационных прогонов.

Успешно изучив тему, Вы:

Получите представление о:

· методе отсечения;

· методе доверительного интервала измеряемого значения;

· методах определения момента вхождения имитируемого процесса в установившийся режим.

Будете знать:

· что такое завершающиеся и не завершающиеся модели;

· что такое неустановившийся и установившийся режимы;

· как задавать начальное состояние имитируемого процесса.

Вопросы темы:

1. Виды моделей и фазы имитации.

2. Настройка параметров и сбор данных запуска.

3. Обеспечение статистической надежности результатов.

Вопрос 1. Виды моделей и фазы имитации.

Проведение имитационных экспериментов может преследовать различные цели, но во всех случаях для решения задач необходимо обеспечить получение нужной совокупности выходных данных, которые будут отвечать требованиям по точности. Существенным фактором, определяющим применяемые методы сбора необходимой информации, является случайный характер протекания имитируемых процессов.

В типичном случае результатом имитационных экспериментов являются (во всяком случае, наряду с прочими результатами) оценки средних значений установившегося режима. Точность результатов, получаемых в результате имитационных прогонов, зависит от двух факторов: во-первых, от устранения влияния на результат первоначальной фазы переходного режима и, во-вторых, от достаточности объема получаемых выходных данных.

Устранение влияния начального переходного периода требует предварительного анализа моделируемой системы. В частности, необходимо установить, насколько существенно сказывается на выходных значениях начальное состояние процесса с тем, чтобы при проведении имитационных экспериментов задавать правильные начальные значения. Установка «хороших» значений начального состояния может способствовать более быстрому вхождению моделируемого процесса в стационарный режим.

С точки зрения наличия в имитационной модели естественным образом определяемой точки завершения модели можно подразделять на завершающиеся и на не завершающиеся.

Временная продолжительность имитации процессов в завершающихся моделях обусловлена временем протекания реального процесса до достижения им своего логического конца. Таковым может быть, например, конец рабочего дня на моделируемом предприятии, окончание исследуемого временного промежутка (скажем, периода пиковой загрузки отделения банка), завершение технологического цикла на производственном участке. Соответственно, время моделирования в таких моделях однозначно определяется внешними условиями.

В не завершающихся моделях четко заданный момент времени окончания процесса отсутствует. К таковым можно отнести производственные процессы на предприятиях с непрерывным циклом, работу операторов «горячей линии», логистические процессы. Время моделирования в таких моделях должно определяться исследователем.

В большинстве случаев значения выходных параметров завершающихся моделей характеризуют переходный (неустановившийся) режим. Это означает, что величина выходного параметра находится в процессе постоянного изменения.

Например, если прослеживать изменение числа клиентов, приходящих в отделение банка в течение одного часа, повторяя наблюдения на протяжении нескольких дней, то зависимость этого значения от времени дня можно представить построенным по результатам наблюдений графиком типа показанного на Рис. 17.

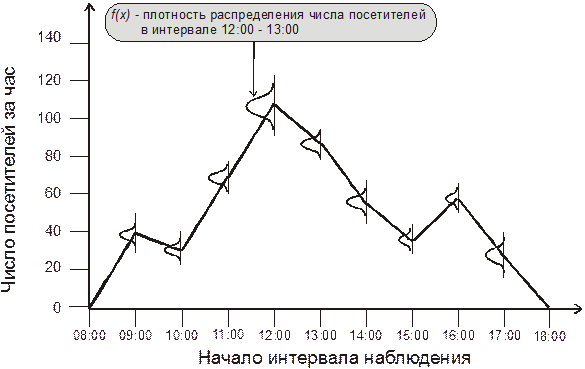
Рис. 17. Зависимость числа посетителей банка в часовом интервале от времени дня

На графике показаны средние значения наблюдавшихся приходов в течение каждого временного промежутка, поскольку число пришедших клиентов в различные дни различно. Этот факт отражается на Рис. 17 отрезками вертикальных линий, график (ломаная) проходит через середины этих отрезков.

Разброс значений числа посетителей в каждом часовом интервале можно описать каким-либо вероятностным распределением. Это показывают на Рис. 17 куполообразные кривые, расположенные слева от вертикальных отрезков, которые являются графическим представлением (в данном случае) нормального закона распределения числа приходов для всех часовых интервалов, но с разными значениями параметров среднего и среднеквадратического отклонения для каждого интервала.

Для завершающихся моделей более типичным является случай, когда имитируемый процесс достигает стационарного (установившегося) режима. Это не означает, что значения выходных параметров вообще не меняются, в стационарном режиме эти изменения подчиняются некоторому распределению, характерному для этого режима.

Например, нормальное функционирование какой-либо единицы оборудования поточной линии на непрерывном производстве может нарушаться случающимися остановками ввиду поломок, нарушений подачи энергопитания и т.п. Однако если проводить наблюдение за показателями производительности работы линии в течение длительного промежутка времени, средние значения этих показателей будут оставаться постоянными (см. Рис. 18).

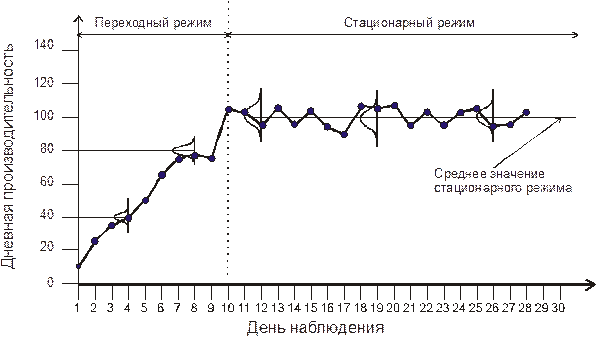
Рис. 18. Зависимость дневной производительности производственной линии от дня наблюдения

Как можно заметить, начиная примерно с десятого дня наблюдения, дневная производительность колеблется в небольшом диапазоне вокруг некоторого среднего значения, представляющего собой значение среднего установившегося режима.

Однако начальное состояние процесса, как видно из рисунка, не совпадает с его состоянием в установившемся режиме, поскольку в реальной системе производственная линия находится в стадии наполнения объектами переработки. Поэтому первая фаза представляет собой фазу начального переходного режима.

В случаях, если процесс достигает установившегося состояния, то в типичных для деловых процессов случаях его состояние в установившемся режиме не зависит от его начального состояния (Рис. 19).

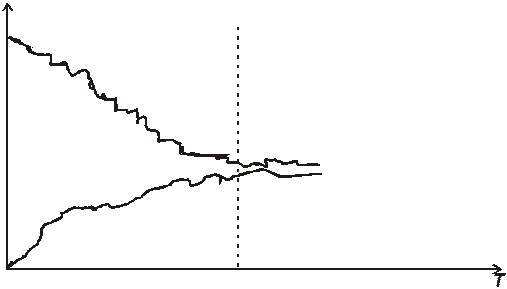
Рис. 19. Реализации процесса с установившимся состоянием

Из рисунка, на котором изображено поведение одного и того же процесса при разных начальных условиях, можно видеть, что, несмотря на разные начальные условия протекания, две реализации одного о того же процесса имеют тенденцию к схожему поведению примерно правее пунктирной линии, проведенной перпендикулярно оси времени. Область левее этой линии представляет собой переходный режим, область правее ее – установившийся режим.

Вместе с тем, в реальной жизни встречаются и другие разновидности режимов. Одним из встречающихся наиболее часто является циклический, где каждый цикл состоит из переходной фазы и фазы стационарной. Примером процессов, для которых характерен такой режим, является работа предприятий с суточным циклом функционирования – в ночное время предприятие не работает, начало каждого рабочего дня представляет собой фазу переходного режима (например, наполнение операционного зала банка клиентами), переходящую в фазу стационарного режима.

Вопрос 2. Настройка параметров и сбор данных запуска.

Поскольку принятие решений на долгосрочную перспективу предполагает длительное протекание и существенную повторяемость исследуемых процессов в будущем, то вполне обоснованным является подход на исследование и оптимизацию показателей эффективности по критерию средних значений. Это означает то, что для получения значений этих показателей нужно проводить имитационные эксперименты вплоть до вхождения их в установившийся режим, а выходные данные, собранные в течение имитации начальной фазы процесса, протекающего в завершающихся моделях, нужно рассматривать как искажающие реальную картину, и учитывать эти данные в итоговой обработке не следует. Для этого можно прибегнуть к одному из двух приемов:

· определение «периода разогрева» модели для исключения его из рассмотрения (прием известен также как метод отсечения);

· установка адекватного начального состояния имитационных прогонов.

Задание «периода разогрева».

В этом случае сбор выходных данных начинается после достижения процессом точки вхождения в стационарный режим, поэтому необходимо определить правило определения этой точки. Можно прибегнуть к одному из нескольких приемов.

· графический метод: ведется визуальное наблюдение за изменением выходных данных;

· эвристический подход: правила, полученные опытным путем;

· статистические методы: используются принципы математической статистики;

· тестирование: проверка выходных данных на наличие в них проявлений переходного периода;

· комбинированные приемы.

Один из наиболее простых и понятных приемов определения продолжительности переходного периода, который часто используется на практике, состоит в визуальном анализе временных зависимостей.

Имитация процесса может начинаться с произвольного начального состояния модели (например, в случае модели центра обслуживания с произвольного, в частности, нулевого числа вызовов, находящихся в очередях на обработку и у операторов). Далее программная модель выполняется в течение достаточно большого временного промежутка (имеется в виду, модельное время). Признаком вхождения имитируемых процессов в стационарный режим может служить динамика значений исследуемых выходных показателей – по мере приближения процесса к установившемуся состоянию значения показателей, рассчитанных по периодам T и T+ΔT (т.е., полученным на какой-то момент моделирования T и на несколько больший момент моделирования T+ΔT ) будут отличаться все меньше и меньше.

Покажем, как можно определить продолжительность периода разогрева на численном примере результатов запусков, приведенных в Табл. 11.

Таблица 11.

Запуск День	1	2	3	4	5	Среднее
1	3	2	5	4	3	3,4
2	22	18	10	24	4	15,6
3	63	42	12	56	47	44,0
4	64	34	142	39	113	78,4
5	60	110	49	104	77	80,0
6	88	54	100	104	121	93,4
7	59	65	70	65	134	78,6
8	105	43	62	56	19	57,0
9	72	133	108	117	150	116,0
10	92	77	93	80	149	98,2

В столбцах 1, 2, 3, 4, 5 таблицы приведены результаты (число обслуженных клиентов) пяти запусков имитации работы по дням (первый столбец) центра технического обслуживания вместе вычисленными средними значениями, занесенными в крайний правый столбец. (Заметим, что реальные имитационные эксперименты не ограничиваются получением значений только одного показателя, как правило, интерес представляет некоторая совокупность выходных параметров.) На основе рассмотрения этих данных нужно определить момент времени, позже которого изменения можно отнести к случайным флуктуациям, которые не характерны для восходящего или нисходящего участков графика (Рис. 20).

Рис. 20. Зависимость производительности от дня наблюдения

Из вида графика можно заключить, что начиная с четвертого дня, наблюдается относительная устойчивость значений. Иначе говоря, «периодом разогрева» процесса следует считать первые три дня, и данные, получаемые на этом временном отрезке моделирования, при обработке результатов учитывать не нужно.

Достоинством рассмотренного метода является его простота. К недостаткам можно отнести то обстоятельство, что момент вхождения в стационарный режим определяется приблизительно, «на глаз» и во многом зависит от опыта и интуиции исследователя, что, естественно, чревато появлением ошибок. Избежать ошибок помогают более строгие методы, базирующиеся на применении формальных правил. К таким методам принадлежит метод скользящего среднего, который находит применение не только в имитационном моделировании. Метод довольно прост в вычислительном отношении, интересующийся читатель может познакомиться с ним в специальной литературе.

Установка начального состояния.

Начальные условия для проведения имитации можно задавать одним из двух способов.

Первый основан на наблюдении процессов моделируемой системы и регистрации состояния системы после ее вхождения в стационарный режим. В случае если модель создается для последующего ее включения в контур принятия решений, как это рассматривалось ранее, то нужные значения могут быть получены автоматически с помощью устройств регистрации и/или программных средств системы мониторинга.

Второй способ основан на применении разработанной программной модели. С помощью последней осуществляется имитация реальных процессов вплоть до момента вхождения в стационарный режим и фиксируются значения данных, задающих состояние модели в этот момент. Далее эти значения используются для задания начального состояния при проведении имитационных экспериментов.

Отметим факторы, которые следует учитывать при решении вопроса о выборе одного из рассмотренных подходов в практических ситуациях.

Метод отсечения не требует проведения наблюдений и экспериментов с моделируемой системой, но для получения нужных сведений требуется провести модельные эксперименты. Если модель достаточно сложна, а время переходного процесса достаточно велико, то для сбора данных может потребоваться значительное время.

Метод установки начального состояния, напротив, не требует вычислительных ресурсов и времени на выполнение программных запусков, но предполагает возможность доступа к реальной системе. В ряде ситуаций это может оказать негативное влияние на работу последней или потребовать разработки специальных средств сбора данных и их обработки для последующего ввода в модель.

В завершение заметим, что все проведенные обсуждения относились к случаям использования имитационных моделей для анализа процессов. Если же модель используется в контуре оперативного управления, то дело обстоит принципиально иначе.

Поскольку задачей оперативного управления является приведение параметров процесса к требуемым значениям, то подход, основанный на изучении поведения модели в условиях установившегося режима, не годится. Более того, установившийся режим может в данных условиях вовсе не достигаться, поскольку основной интерес с точки зрения задачи оперативного управления представляет состояние процесса в ближайшем будущем. Поэтому имитационная модель, используемая для оперативного управления, должна принципиально применяться для имитации процессов именно в переходном режиме.

Вопрос 3. Обеспечение статистической надежности результатов.

Статистическую полноту собираемых в результате экспериментов данных можно обеспечить одним из двух способов: либо выполняя один длительный прогон модели, либо многократным повторением прогонов.

В случае не завершающихся моделей экспериментатор может выбирать как первый, так и второй способ.

В случае завершающихся моделей единственно возможным является второй способ, предполагающий получение нескольких реализаций (реплик). Для получения независимых запусков необходимо обеспечить независимость задаваемых начальных условий, для чего используются случайные выборки из распределений.

При выборе первого подхода необходимо определить нужное число запусков. В общем случае число запусков зависит от того, насколько сильно разбросанными оказываются значения выходных параметров, получаемые при отдельных запусках программной модели. В случае если разброс велик, запусков нужно делать больше.

Для определения числа запусков используется несколько способов.

Эмпирический метод.

В этом случае решение вопроса определения числа запусков не предполагает анализ выходных данных отдельных запусков и основано на опыте исследователя и соображениях общего характера.

К их числу, частности, можно отнести правило, согласно которому ни при каких условиях не следует ограничиваться единственной реализацией, поскольку результаты прогона могут оказаться «нетипичными» за счет «нетипичной» комбинации значений входных параметров или начального состояния, выбранных для этого прогона.

Другие рекомендации содержат конкретные значения (или диапазона значений) для числа запусков. Одним из вариантов рекомендации является рекомендация выбирать число запусков от трех до пяти.

Графический метод.

Этот метод достаточно прост и основан на анализе результатов отдельных реализаций. Для эффективной работы метода рекомендуется предварительно получить результаты, по меньшей мере, 10 реализаций.

Поясним его суть на примере.

В Табл. 12 представлены результаты (число клиентов, пришедших в центр обслуживания) отдельных запусков модели (второй столбец) и значения кумулятивного среднего (третий столбец).

Таблица 12.

Реализация	Показатель	Кумулятивное среднее
1	99	99,0
2	94	96,5
3	95	96,0
4	87	93,8
5	92	93,4
6	89	92,7
7	99	93,6
8	95	93,8
9	88	93,1
10	101	93,9
11	94	93,9
12	92	93,8
13	93	93,7
14	88	93,3
15	91	93,1
16	92	93,1
17	92	93,0
18	96	93,2
19	93	93,2
20	87	92,9

Кумулятивное среднее для реализации с номером k рассчитывается как среднее по реализациям 1, 2 …,k. На Рис. 21 показан график кумулятивного среднего.

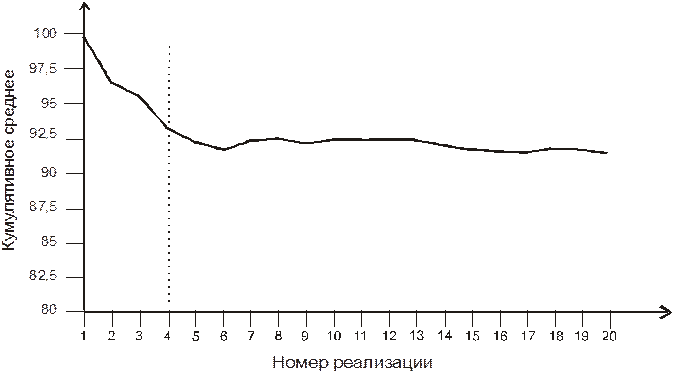
Рис. 21. Зависимость кумулятивного среднего от числа реализаций

График приобретает вид прямой, параллельной оси абсцисс, начиная с реализации 4, что и следует считать минимально необходимым числом реализаций.

Метод доверительного интервала.

Метод доверительного интервала принадлежит к методам математической статистики и дает возможность оценить число реализаций, необходимых для достижения нужной степени уверенности, которая выражается количественно величиной доверительной вероятности, в том, что значение исследуемого показателя принадлежит определенному интервалу значений. Очевидно, что чем большую уверенность мы хотим иметь, и чем более узким интервал для значений показателя будет задаваться, тем большее число реализаций нам потребуется.

В предположении нормального закона распределения значений показателя нижнюю () и верхнюю () границы доверительного интервала можно найти, используя выражение для распределения Стьюдента:

где

- среднее выборочное значение исследуемого (выходного) показателя, - половина величины доверительного интервала.

Величина полуинтервала находится по формуле:

где

n-число реализаций;

- значение распределения Стьюдента с (n-1) степенями свободы и уровнем значимости α/2;

-среднеквадратическое отклонение выборки, которое находится по формуле:

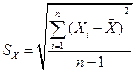где

- отдельное значение выборки (реализации).

Одной из наиболее популярных величин для уровня значимости в практике имитационного моделирования практики является величина 5% (часто используются также значения 10 %, 1 %, и 0,1 %). Это можно трактовать как утверждение о том, что величина исследуемого показателя с вероятностью 95% принадлежит доверительному интервалу. Поскольку доверительный интервал задается нижней и верхней границами, уровень значимости делится на 2, поэтому для уровня значимости 5% из распределения Стьюдента находится значение для уровня значимости 2,5%.

Значения распределения Стьюдента можно найти, используя специальные таблицы или статистические функции программных пакетов (например, функции ТТЕСТ, СТЬЮДРАСП и СТЬЮДРАСПОБР в пакете Excel).

Выбор способа получения значений (одна длительная реализация или совокупность реализаций) во многом определяется как типом модели, так и имеющимися в распоряжении исследователя ресурсами.

Так, для завершающихся моделей, как уже отмечалось, выбор, фактически, отсутствует.

В случае не завершающихся моделей в идеальном варианте желательно произвести несколько длительных прогонов, но это может оказаться невозможным в силу временных ограничений и ограничений на вычислительные ресурсы.

К преимуществам подхода на основе проведения совокупности прогонов модели следует отнести возможность получения количественных оценок получаемых результатов на основе методов математической статистики, к недостаткам – необходимость многократно (при каждой имитации) непроизводительно тратить время на вхождение имитируемого процесса в стационарный режим.

К преимуществам подхода на основе одной длительной реализации относится экономичность в смысле расходования машинного времени (вхождение имитируемого процесса в стационарный режим происходит однократно) и большая наглядность, как самого процесса (если используется имитация), так и его результатов. Однако дать количественную (статистическую) оценку полученным результатам по одной реализации практически невозможно.

В большинстве случаев нужно находить оптимум с учетом преимуществ и недостатков обоих подходов и имеющихся ограничений.

Выводы:

1. Типичным видом результата отдельного имитационного прогона является оценка среднего значения какого-либо показателя. Однако для обеспечения необходимой точности и надежности полученных данных необходимо предусмотреть ряд мер, учитывающих специфику имитационного эксперимента. Отсутствие этих мер может обесценить получаемые результаты.

2. В зависимости от характера процессов, протекающих в моделируемой системе, модели подразделяются на завершающиеся и не завершающиеся. Отнесение модели к одному из этих типов в значительной степени определяет выбор методов организации имитационных прогонов.

3. Важное значение для правильной организации сбора данных является учет поведения имитируемого процесса, который, в общем случае, может находиться в неустановившемся и установившемся режимах. Для определения момента перехода процесса из одного режима в другой применяются специальные методы.

4. Данные, получаемые в результате имитации, могут трактоваться как случайные выборки, поэтому необходимо проводить оценивание их статистической надежности. Для решения этой задачи могут применяться как нестрогие, так и строгие подходы, в основе которых лежат методы математической статистики.

Вопросы для самопроверки:

1. От чего зависит выбор методов сбора выходных данных имитационного эксперимента?

2. Что в типичном случае является результатом имитационных экспериментов?

3. На какие типы можно разделить модели в зависимости от наличия или отсутствия естественной точки завершения?

4. Что такое завершающиеся модели? Приведите примеры завершающихся моделей.

5. Что такое не завершающиеся модели? Приведите примеры не завершающихся моделей.

6. Какие модели можно отнести к циклическим? Приведите примеры циклических моделей.

7. Что называется переходным (неустановившимся) режимом?

8. Что называется стационарным (установившимся) режимом?

9. Какой характер может носить график выходных параметров не завершающихся моделей?

10. Какие фазы характерны для не завершающихся моделей?

11. Какие методы устранения искажений, вносимых фазой переходного процесса, используются на практике?

12. В чем заключается сущность метода отсечения?

13. В чем заключается сущность метода задания адекватного начального состояния?

14. Какие используются методы определения точки вхождения процесса в стационарный режим?

15. Какой режим имитации должна обеспечивать модель, используемая для оперативного управления?

16. Какие используются методы определения адекватных начальных условий?

17. Какими способами можно обеспечить статистическую полноту данных, собираемых в результате имитационных экспериментов?

18. Какие существуют методы для определения числа запусков, необходимых для получения состоятельной оценки?

19. Что собой представляет графический метод нахождения требуемого числа имитационных запусков?

20. В чем состоит сущность метода доверительного интервала?

21. Что означают понятия доверительного интервала и уровня значимости?

22. Как зависит число реализаций имитационных запусков от величины доверительного интервала и уровня значимости?

23. Как определяются границы доверительного интервала показателя по заданной величине уровня значимости?

24. Какими преимуществами и недостатками обладает метод доверительного интервала?

25. Какими преимуществами и недостатками обладает метод, основанный на одной длительной реализации?

Литература по теме:

Основная литература:

Дополнительная литература:

Практические задания:

1. Определите тип имитационной модели для следующих ситуаций:

· моделируется работа сервисного центра с целью оценить его среднюю производительность;

· моделируется работа металлургического завода с целью нахождения нужных режимов работы нового оборудования;

· моделируется работа крупного универсама с целью определить наиболее подходящее число касс в часы пиковой загрузки;

· моделируется работа пользователей корпоративной информационной сети с целью определения требований к параметрам оборудования.

2. Для представленных графиков временной зависимости значения выходного показателя имитационного прогона определите тип модели (завершающаяся или не завершающаяся) и характер процесса (переходный, установившийся, циклический):

3. Для последовательности значений выходного параметра, относящихся к последовательным часам наблюдения, которые представлены в таблице, найдите момент вхождения процесса в стационарный режим (совет: используйте возможности табличного редактора Excel).

0,0	97,2	139,2
0,0	123,2	132,4
27,2	128,8	122,0
138,8	93,2	127,2
130,0	145,6	152,4
120,8	140,0	151,6
104,0	135,6	148,0
99,2	142,0	153,6
67,6	159,2	144,4
83,2	156,0	138,8
68,0	136,8	122,8
130,0	120,4	135,2
128,4	90,8	159,2
127,2	154,0	166,8
139,6	142,8	134,8
142,8	116,4	121,2
134,8	105,2	90,4
126,4	100,0	105,6
130,8	107,2	78,0
146,0	83,2	112,8
132,0	118,4	158,4
144,8	130,4	147,2
140,0	143,6	142,8
127,2	151,2	138,4
87,2	136,8	117,6

Тема 7. Стратегическое планирование имитационных экспериментов

Цели изучения темы:

· изучить возможные формулировки глобальной цели имитационных экспериментов и подходы к ее достижению.

Задачи изучения темы:

· познакомиться с возможными типами целей имитационного моделирования;

· познакомиться с основными задачами, которые необходимо решить для достижения целей;

· познакомиться с основными подходами к решению задач.

Успешно изучив тему, Вы:ипьалдипл

Получите представление о:

· интерактивном и пакетном режимах проведения имитационных экспериментов;

· важности решения задачи выбора существенных факторов;

· возможных подходах к планированию экспериментов для нахождения наилучшего решения.

Будете знать:

· как использовать метод построения плана для определения совокупности существенных факторов;

· как применяется метод доверительного интервала для выбора вариантов на основе оценивания показателей.

Вопросы темы:

1. Задачи стратегического планирования.

2. Типы имитационных экспериментов.

3. Выделение существенных факторов.

4. Сравнение и оптимизация.

Вопрос 1. Задачи стратегического планирования.

Типичным вопросом, относящимся к сущности имитационного моделирования, является вопрос о том, в чем состоит различие между имитационным моделированием и оптимизацией. Ответ на вопрос можно пояснить с помощью простого уравнения:

Y = F (X)

В этом уравнении X представляет собой вход модели, сама модель представлена функцией F, а Y представляет собой выход модели. Например, X может означать целевое значение объема складских запасов для процесса управления запасами, функция F описывает процесс пополнения запасами, Y означает результирующее значение запасов. Для целей изучения поведения функции F (модели) могут использоваться как методы оптимизации, так и имитационное моделирование.

Одним из возможных и очень часто применяемых способов понять поведение функции F является проведение имитационных экспериментов на модели, целью которых является ответ на вопрос что-если, для чего в модель вводятся различные значения X, по которым определяются соответствующие значения Y. Иначе говоря, вопрос можно сформулировать так: Какой будет величина Y, если значением X будет 4? В реальных условиях наборов возможных значений входа (X) и соответствующих им значений выхода (Y) существует много, поэтому вид функции (F) может оказаться довольно сложным.

Другим способом изучения функции F является проведение имитационных экспериментов на модели, целью которых является ответ на вопрос если-то, что, для чего в модели задается целевое значение выхода Y и осуществляется поиск значений входа X, которые приводят к целевому значению Y. Вопрос можно поставить, например, так: если желаемое значение Y равно 10, то каким должно быть значение X? Иначе говоря, количество входов (X) и выходов (Y) на практике может быть довольно большим, модель сложна, поэтому необходимо применять специальные методы поиска ответа на этот вопрос, чтобы его можно было найти за приемлемое время.

Ценность задачи оптимизации состоит в том, что результатом ее решения является значение входа модели или, после интерпретации и/или преобразования этого значения входа реальной (моделируемой) системы, которое обеспечивает получение желаемых результатов. Имитационные эксперименты можно использовать для достижения той же цели, но в этом случае потребуются понести значительно большие затраты, чтобы имитировать множество альтернатив для нахождения того значения X, которое обеспечивает получение целевое значение Y.

Таким образом, с помощью оптимизации можно получить прямой ответ на вопрос о том, как получить целевое значение. Однако в типичном случае для оптимизации на практике используются весьма упрощенные модели, поэтому полной уверенности в том, что решение действительно лучшее может не быть. Имитационное моделирование ценно тем, что структуру и степень детализации модели можно приблизить как угодно близко к моделируемой системе. В частности, с помощью имитационной модели можно получить сведения о возникающих эффектах и причинах их появления, на основе которых объяснить наличие оптимума. Но, с другой стороны, имитация с помощью детализированной модели может занять много времени и сделать эту модель практически бесполезной.

Вопрос 2. Типы имитационных экспериментов.

Параметры, значения которых задаются в процессе проведения экспериментов с целью изучения их влияния на показатели функционирования системы, будем называть факторами.

Факторы могут быть двух типов.

Количественные факторы могут измеряться с помощью количественной шкалы. Например, величина интервала между приходами клиентов в центр технического обслуживания.

Качественные факторы численного выражения не имеют. Например, порядок обслуживания очереди в центре техобслуживания может производиться как в порядке поступления клиентов, так и по приоритету более коротких заявок или по какому-либо другому принципу. Тем не менее, каждый из этих вариантов должен быть каким-то образом задан.

С целью задания их значений для факторов применяется понятие уровня. Для количественного фактора его уровнем является непосредственно его значение, качественный уровень задается кодовым обозначением. Например, для фактора, обозначающего правило выбора клиентов из очереди, правило выбора в порядке поступления клиентов может задаваться уровнем 1, а приоритетная дисциплина - уровнем 2.

Выходные величины, значения которых получаются в результате прогонов модели, называют откликом. Отклик может состоять из одной или нескольких выходных переменных.

Описание условий для запуска имитационной модели будем называть также сценарием запуска. Сценарий может трактоваться как заданная совокупность определенных факторов вместе со значениями уровней факторов. Изменение уровня какого-либо фактора, таким образом, означает изменение сценария.

Имитационные эксперименты можно проводить на основе двух различных подходов – интерактивного и пакетного.

Интерактивные эксперименты сводятся к наблюдению за ходом модельной имитации реальных процессов и внесению изменений в модель с целью изучить эффект от этих изменений. Например, добавляя или убирая некоторое число операторов в систему технического обслуживания можно получить представление о минимально достаточном их количестве с точки зрения требований к качеству обслуживанию (скажем, ко времени ожидания клиентами получения обслуживания).

Чтобы обеспечивался такой режим, необходимо, чтобы время каждого прогона было достаточно небольшим, что в ряде случаев приводит к менее надежным результатам (в силу причин, которые рассматривались ранее). Поэтому такой режим работы с моделью целесообразен для получения представления об основных механизмах реальных процессов или выяснения основных направлений их возможных улучшений.

Более детальную и статистически состоятельную информацию можно получить только на основе пакетных прогонов модели. В этом случае эксперименты реализуются на основе заранее подготовленного плана, в котором определяется число необходимых прогонов (либо условие их прекращения в некоторый момент) и значения уровней всех используемых факторов для каждого из прогонов. Время моделирования и число необходимых запусков задаются на основе правил, которые обсуждались ранее.

Для обработки данных, полученных в итоге проведенных экспериментов, можно использовать средства общего назначения, например, Excel (в относительно несложных экспериментах с небольшими объемами данных) или Matlab (Matrix Laboratory, пакет и язык программирования для проведения сложных инженерных расчетов и анализа данных).

Средствами обработки результатов экспериментов обладают также и современные специализированные системы имитационного моделирования. Они предоставляют возможность не только формировать план запусков, сохранять массивы выходных данных и проводить их статистическую обработку, но и составлять расписание прогонов и осуществлять запуски в соответствии с расписанием. Последняя возможность, помимо прочего, довольно удобна и с практической точки зрения, поскольку длительные по времени прогоны могут проводиться в ночные часы и или в выходные дни, не занимая вычислительные ресурсы в рабочее время.

Вопрос 3. Выделение существенных факторов.

Большое количество факторов, используемое в процессе имитационных экспериментов, может значительно усложнить решение поставленных задач (далее будет приведен численный пример, наглядно иллюстрирующий это утверждение). Поэтому одной из первых задач, решаемых исследователем перед началом проведения имитационных экспериментов, является задача определения среди всего многообразия факторов только тех, влияние которых на величину отклика модели оказывается существенным.

Для определения совокупностей существенных факторов используются несколько подходов. Кратко остановимся на каждом.

Анализ данных.

В ряде случаев бывает возможным вынести суждение относительно влияния факторов на отклик непосредственно из выходных данных прогонов. Однако такой способ, разумеется, довольно ненадежен и может применяться лишь к ограниченной области изменения факторов.

Экспертное оценивание.

Вывод относительно значимости факторов в этом случае выносится на основе сведений, получаемых от специалистов в данном вопросе (при помощи опросов, интервью и т.п.). Источником информации могут быть, например, операторы, работающие в центре обслуживания, или системные аналитики и программисты сопровождения корпоративной информационной системы. Вместе с тем, сведения, предоставляемые отдельными специалистами, в типичном случае могут относиться лишь к некоторым специфическим аспектам функционирования моделируемой системы, хорошо знакомым данному лицу.

Экспериментальное оценивание.

Этот метод предполагает проведение специальных экспериментов на модели с целью сбора необходимых данных относительно влияния факторов на отклик. Значения факторов задаются в экспериментах на различных уровнях.

Несмотря на то, что предварительный эксперимент требует дополнительных временных затрат, результаты, которые можно получить с его помощью, наиболее точны и информативны.

Посмотрим, каким образом можно спланировать и реализовать план экспериментов для выделения существенных факторов модели на основе так называемого плана, где k означает число изучаемых факторов. Планы и результаты их выполнения заносятся в таблицу. Знак «+» в столбцах для факторов в таблице означает, что фактор в данном запуске (сценарии, плане) берется на верхнем уровне значимости, знак «–» означает, что фактор в данном запуске берется на нижнем уровне значимости (в случае качественного фактора отнесение значения к верхнему или нижнему уровню может делаться по усмотрению исследователя).

Для примера рассмотрим случай, когда число факторов равно трем. В Табл. 13 показан план имитационных экспериментов для этого случая.

Таблица 13.

План	Факторы			Отклик
План	1	2	3	Отклик
1	−	−	−	R1
2	+	−	−	R2
3	−	+	−	R3
4	+	+	−	R4
5	−	−	+	R5
6	+	−	+	R6
7	−	+	+	R7
8	+	+	+	R8

Общее число планов в данном случае (k=3) равно. В столбец «Отклик» заносятся результаты имитационных прогонов, на основе которых можно вычислить величину эффекта (изменение функции отклика) , который вызван изменением уровня фактора.

Эта величина может быть рассчитана для каждого фактора как среднее арифметическое разностей значений функции отклика для уровней фактора «+» и «–» при сохраняющихся значениях уровней прочих факторов. В частности, для фактора 1 эта величина, называемая главным эффектом, найдется как:

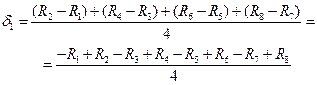
Разности в каждой паре круглых скобок представляют собой изменения функции отклика, вызванные только изменением уровня фактора 1 с нижнего на верхний, поскольку уровни других факторов сохраняются неизменными.

Можно заметить, что знаки у значений функции отклика, входящих в выражение для нахождения, совпадают со знаками для уровня фактора 1. Поэтому можно записать выражения для .

Найденные величины позволяют упорядочить факторы по степени влияния на отклик и отобрать наиболее важные. Более того, на основании данных Табл. 13 можно определить и комбинированные эффекты, которые обусловлены взаимодействиями факторов.

Например, в рассматриваемом примере эффект взаимодействия второго и третьего факторов можно найти на основе выражения:

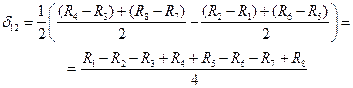
Это выражение представляет собой половину разницы между средним величины отклика при изменении уровня первого фактора с «−» на «+», когда второй фактор берется на уровне «+», и средним величины отклика при изменении уровня первого фактора с «−» на «+», когда второй фактор берется на уровне «−». Нетрудно заметить, что знаки перед значениями функции отклика, стоящими в дроби после второго знака равенства, получаются перемножением знаков, записанных в столбцах таблицы для первого и второго факторов.

Рассмотрим простой пример. Пусть необходимо выяснить влияние на отклик (среднее время ожидания клиентов в очереди в минутах) двух факторов в модели системы обслуживания, к которым относятся дисциплина обслуживания диспетчером клиентов, приходящих в систему (неприоритетное -»−», приоритетное -»+»), и средняя продолжительность обслуживания клиента у диспетчера. Приоритетная дисциплина означает, что обслуживание клиента с меньшим приоритетом в случае прихода более приоритетного клиента будет прервано и продолжится после окончания обслуживания приоритетного клиента. Результаты имитационных экспериментов (значения функции отклика) приведены в Табл. 14.

Таблица 14.

План	Факторы		Отклик
План	1	2	Отклик
1	−	−	9,72
2	+	−	8,30
3	−	+	9,90
4	+	+	8,60

Находим:

Из полученных значений можно заключить, уменьшение среднего времени обслуживания клиентов диспетчерами и совместный эффект сказываются на среднем времени нахождения клиентов в очереди к диспетчеру очень незначительно, в то время как установление приоритетной дисциплины приведет к ощутимому (на 1,38 минут) уменьшению среднего времени ожидания.

При использовании описанного подхода необходимо учитывать ряд обстоятельств.

В частности, в случае присутствия эффектов взаимодействия факторов определение главных эффектов может осложниться, поскольку эффект от изменения уровня какого-либо фактора будет зависеть от уровней других факторов.

Относительно надежные выводы можно делать только применительно к уровням факторов, которые входят в диапазон, определяемый крайними (нижним и верхним) уровнями, для которых проводились испытания.

В случае большой разницы между нижним и верхним уровнями фактора существует большая вероятность, что характер изменения функции отклика на промежуточных уровнях может отличаться от монотонного. Иначе говоря, наибольший эффект может получаться от изменения значения фактора на каких-то промежуточных уровнях.

Вопрос 4. Сравнение и оптимизация.

Конечную (стратегическую) цель моделирования можно отнести к одному из двух типов – сравнению или оптимизации.

В случае сравнения задача моделирования формулируется как сравнительное оценивание качества (по выбранным показателям) нескольких заранее заданных вариантов.

Например, если производственная компания планирует реорганизовать свою технологию или организует новое производство, то ему может потребоваться сделать выбор из нескольких предлагаемых на рынке производственных линий и моделей оборудования. Число изучаемых вариантов обычно четко задано и невелико, поэтому план проведения модельных экспериментов непосредственно следует из постановки задачи и специального рассмотрения не требует.

Другой, более сложной задачей является задача поиска наилучшего (в заданном смысле) решения в некоторой области (оптимизации). Для пояснения природы этой сложности рассмотрим простой пример.

Пусть некоторой компании требуется решить вопрос о модернизации своей корпоративной информационной системы путем оснащения ее новым оборудованием с одновременным определением мест (своих филиалов), в которых целесообразно установить терминалы для доступа к информационным ресурсам. Предположим, что к факторам, определяющим предпочтительность каждого из вариантов, относятся модель устанавливаемого сервера, модель массива внешних дисков (RAID) и идентификация филиалов, в которых устанавливаются терминалы. Для каждого фактора задано несколько уровней:

· Модель сервера (фактор 1) может выбираться из пяти возможностей (число уровней равно 5).

· Модель RAID (фактор 2) может выбираться из пяти возможностей (число уровней равно 5).

· Компания имеет шесть филиалов (фактор 3, число уровней, которое, как нетрудно видеть, находится как).

В итоге получаем комбинаций (сценариев). Если предположить, что на каждый сценарий потребуется всего пять реализаций, а каждая реализация занимает всего три минуты, то общее время имитационных прогонов составит , что равно 22 рабочим дням (считая продолжительность рабочего дня равной восьми часам), или (с учетом выходных) ровно одному календарному месяцу.

Если учесть, что приведенный пример очень сильно упрощает реальную ситуацию (факторов и уровней на практике значительно больше, а имитационные прогоны более продолжительны), то становится совершенно очевидной невозможность подхода к решению задачи оптимизации на основе полного перебора всех возможных сценариев.

Рассмотрим возможные подходы к решению задач.

Задача в случае сравнительного анализа заключается в сравнении средних значений какого-либо показателя (функции отклика). Однако заключение о предпочтительности какого-то из анализируемых вариантов перед другим требуют осторожности.

Пусть, например, измеренное в результате имитационных экспериментов среднее значение функции отклика (показателя) одного из вариантов () оказалось равным 70, а второго () – 80. Вывод о том, что необходимо выбирать второй вариант может оказаться необоснованным, если оставить без рассмотрения доверительные интервалы полученных значений, что поясняется Рис. 22.

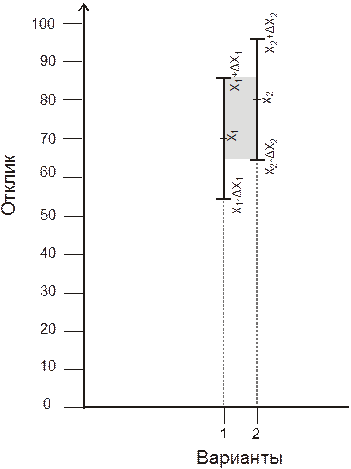
Рис. 22. Сравнение вариантов

Из рисунка видно, что максимальное значение показателя внутри доверительного интервала в первом варианте () оказывается большим возможных значений показателя из доверительного интервала второго варианта. Т.е., возможные значения показателей могут принадлежать одному участку, показанному на Рис.22 (доверительные интервалы перекрываются). Следовательно, сделать статистически надежный вывод в данном случае нельзя.

Для надежного результата нужно учитывать все факторы, которые могут влиять на надежность принимаемого решения. При практическом сопоставлении альтернатив необходимо оценивать степень отличия средних значений показателя (функции отклика), величину доверительного интервала и число выполненных реализаций.

Статистически значимое сравнение двух вариантов можно провести на основе определения границ доверительного интервала расхождений между значениями измеряемого показателя. Для этого используются следующие выражения (похожие на использованные ранее при рассмотрении доверительного интервала):

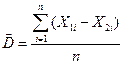
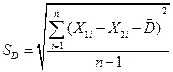
где

- среднее значений расхождений между значениями откликов вариантов 1 и 2;

- отдельное значение отклика в i-ой реализации (прогоне) первого варианта;

- отдельное значение отклика в i-ой реализации (прогоне) второго варианта;

- среднеквадратическое отклонение расхождений, n-число реализаций (одинаковое для обоих вариантов).

В зависимости от значений и могут представиться три возможных варианта:

В этом случае с заданной доверительной вероятностью (например, 95%), вариант 1 менее предпочтителен, чем вариант 2.

В этом случае с заданной доверительной вероятностью сделать вывод относительно предпочтительности одного из вариантов нельзя.

В этом случае с заданной доверительной вероятностью вариант 1 более предпочтителен, чем вариант 2.

Существуют также и методы, в которых предположение о равенстве числа реализаций не является обязательным.

Рассмотренный метод сравнения двух вариантов легко распространяется на случай решения задачи сравнения нескольких вариантов.

Цель решения задачи оптимизации состоит в нахождении сочетания уровней факторов, доставляющих максимум функции отклика.

Если подходить к решению задачи с точки зрения ее математической постановки, то оптимизация состоит в нахождении точки максимума (например, величины средней годовой прибыли предприятия или объема выпускаемой продукции на производственной линии) или минимума (например, среднего времени ожидания требований на обслуживание в очереди или себестоимости единицы продукции) целевой функции. В типичном случае, задача оптимизации должна решиться в условиях действия ограничений, в первую очередь, ограничений на ресурсы.

Поскольку, как уже было ранее отмечено, полный перебор всех возможных сценариев имитационных прогонов невозможен, то на практике используются методы для сокращения числа сценариев. Эти методы можно подразделить в зависимости от строгости на три группы.

Эвристические методы.

Отличие в подходе к решению оптимизационной задачи на основе имитационных экспериментов обусловлено отсутствием формальной постановки, иначе говоря, вид целевой функции неизвестен. Выходом из этой ситуации часто служат эвристические методы, которые дают возможность найти «хорошее» решение, но не гарантируют его оптимальность.

Проиллюстрировать возможный вариант такого подхода можно с помощью Рис. 23, на котором показана зависимость отклика от одного фактора.

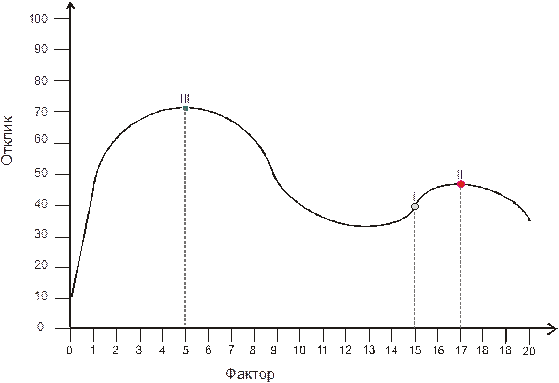
Рис. 23. К возможным ошибкам эвристического алгоритма

График функции отклика, показанный на Рис. 23 (неизвестный исследователю), имеет два экстремума («горба»). Представим себе, что имитационные эксперименты начинаются с точки I. Эвристическое правило состоит в том, чтобы, осуществив пробные запуски увеличенным и уменьшенным на величину Δ со значениями фактора (в данном примере в точках с уровнями фактора 14 и 16, полагая Δ=1), выбирать в качестве следующей экспериментальной точки ту из двух испытанных, в которой отклик больше. В данном случае, это точка с уровнем фактора 16.

Продолжая испытания в направлении увеличения отклика (т.е., устанавливая уровень фактора на Δ больше), попадаем в точку II (с уровнями фактора 17). Дальнейшее увеличение фактора приведет к уменьшению отклика, поэтому процедура проверки, согласно правилу, здесь остановится.

Как видим этот метод, как всякий эвристический метод, не позволил получить наилучшее в строгом смысле решение: результатом проведенных экспериментов будет уровень фактора, обеспечивающий значение отклика в точке II, в то время как большее значение соответствует точке III, которая в случае применения такой процедуры будет пропущена. Дополнительным недостатком применения эвристических методов являются издержки, связанные с необходимостью производить отдельные запуски для каждой пробной попытки.

Тем не менее, в ряде случаев применение таких методов оправдано, и ряд пакетов имитационного моделирования включает средства для планирования и проведения экспериментов на основе эвристических алгоритмов.

Однако следует иметь в виду, что в качестве функции отклика в этом случае выступает одно единственное значение, т.е., используется скалярная функция. Нахождение решений в тех случаях, когда необходимо учитывать сразу несколько показателей (например, величину получаемой прибыли и уровень безопасности), требует применения подходов на основе векторной оптимизации или методов свертки показателей, которые рассматриваются в системном анализе.

Выводы:

1. Стратегическими целями проведения имитационных экспериментов могут быть ответы на вопросы либо относительно возможных последствий в случае принятия некоторого решения, либо поиск условий, обеспечивающих наилучший или близкий к нему эффект. Поставленная цель определяет глобальный подход к организации и проведению модельных экспериментов.

2. В зависимости от цели и практических возможностей имитационные эксперимент могут проводиться в интерактивном или пакетном режиме. Первый режим применяется преимущественно в случае для получения информации о возможном поведении моделируемой системы в различных ситуациях, второй используется для нахождения достаточно точных и статистически надежных решений. В силу своего назначения проведение экспериментов в пакетном режиме основано на их предварительном планировании.

3. Важным обстоятельством, определяющим временные и прочие затраты на проведение экспериментов, является правильное определение совокупности факторов, влияние которых на отклик будет изучаться в процессе имитационных экспериментов. Для выбора существенных факторов применяются различные методы, примером которых является часто используемый метод под названием плана .

4. Задача для имитационных экспериментов может сводиться к задаче принятия решения, состоящей в выборе одного из возможных кандидатов в соответствии с результатами оценки качества решений в каждом из случаев. Надежность оценивания должна обеспечиваться специальными мерами, которые учитывают случайный характер получаемой оценки. Одним из методов, позволяющих решить задачу, является метод доверительного интервала.

5. В случае, когда конечной целью эксперимента, является нахождение наилучшего решения, могут применяться как эвристические, так и точные методы. При выборе метода необходимо принимать в расчет то, что эвристические алгоритмы не гарантируют получения строго оптимального решения, а неудачно выбранный метод математической оптимизации может оказаться практически неприемлемым из-за чрезмерных временных затрат. В зависимости от конкретных требований к результату и сложности модели удовлетворительное решение может быть найдено среди методов, предлагаемых теорией планирования эксперимента.

Вопросы для самопроверки:

1. Какого типа вопросы могут ставиться перед имитационной моделью?

2. Какого характера эксперименты проводятся для ответа на вопрос типа что-если?

3. Какого характера эксперименты проводятся для ответа на вопрос типа если-то, что?

4. Что является конечной целью решения задачи оптимизации?

5. Что является ограничением для применения математических (аналитических) методов оптимизации?

6. Что называется факторами?

7. Какие бывают типы факторов?

8. Что называется уровнем фактора?

9. Что такое отклик?

10. Что понимается под термином интерактивные эксперименты?

11. Что понимается под термином пакетные эксперименты?

12. Какими средствами можно пользоваться для обработки результатов пакетных экспериментов?

13. В чем заключается необходимость выделять существенные факторы?

14. Какие методы могут использоваться для выделения существенных факторов?

15. В чем состоит идея оценивания значимости факторов на основе экспериментального оценивания?

16. Каким образом строится план для экспериментального оценивания факторов?

17. Что такое главный и комбинированный эффекты??

18. Какие обстоятельства требуется принимать во внимание при использовании подхода на основе плана ?

19. Какого типа конечные цели могут ставиться для имитационных экспериментов?

20. В чем заключается основная сложность решения задачи оптимизации?

21. Что следует принимать в рассмотрение при решении задачи сравнения (выбора)?

22. Каким образом оцениваются границы доверительного интервала расхождений между сравниваемыми образцами?

23. Какие случаи в зависимости от значений и могут представиться и каким будет вывод в каждом из этих случаев?

24. Какие подходы для поиска наилучших решений применяются на практике?

25. Что может являться причиной ошибочных (не строго оптимальных) решений в случае применения эвристических алгоритмов?

26. Как можно решать задачи многокритериальной (векторной) оптимизации?

Литература по теме:

Основная литература:

1. Емельянов А. А. Имитационное моделирование экономических процессов/ А. А. Емельянов, Е.А.Власова, Р.В.Дума. – М.: Финансы и статистика, 2009 – 416 с.

2. Ходасевич Г.Б. Планирование эксперимента Электронный ресурс. / Г.Б. Ходасевич Режим доступа: http://pds.sut.ru/pe/

3. Ю.Адлер Планирование экспериментов при поиске оптимальных условий./Адлер Ю.П. и др. – М.: «Наука», 1976. – 279 с.

Дополнительная литература:

1. Анфилатов В.С., Емельянов А.А., Кукушкин А.А. Системный анализ в управлении. – М.: Финансы и статистика, 2002. – 368 с.

2. Асатурян В.И. Теория планирования эксперимента. – М.: Радио и связь, 1983. – 248 с.

Практические задания:

1. Используя данные имитационных экспериментов, проведенных для выявления значимости факторов

N			Отклик
1	−	−	114,5
2	+	−	121,9
3	−	+	100,7
4	+	+	111,5

проранжируйте факторы имитационной модели.

2. С целью сопоставления двух вариантов решений проведено 10 имитационных запусков. Результаты (значения показателя качества для первого и второго вариантов решения) представлены следующей таблицей:

N
1	138,7	140,1
2	147,4	147,4
3	151,6	151,6
4	145,7	146,9
5	127,3	127,7
6	154,6	154,7
7	123,5	124,4
8	134,2	135,5
9	146,5	146,6
10	147,5	148,1

Основываясь на собранных в результате эксперимента данных, проверьте на уровне значимости 5% гипотезу о предпочтительности второго варианта решения перед первым.

Приложение

Основные сведения из теории вероятностей.

В силу случайного характера событий деловых процессов в моделируемых системах (моменты времени прихода и типа очередной заявки входящего потока, маршрута следования отдельной единицы в цепочке поставок, продолжительность обслуживания в узле сети и т.п.), имитировать процессы в таких системах и анализировать их показатели можно только с помощью вероятностных величин. Для этого используется аппарат теории вероятностей.

События и вероятность.

Если событие А при некотором испытании может как произойти, так и не произойти, то такое событие называется случайным.

Случайному событию приписывается некоторое число между 0 и 1, называемое его вероятностью и обозначаемое через Р(А).

Вероятность того, что событие А не произойдет, обозначается Р(Ã):

Если результаты опыта сводятся к схеме случая и общее число случаев (опытов) равно N, то вероятность события А выражается (оценивается) как:

где

NA-число случаев благоприятных событию А (или число случаев, при которых событие А произошло).

События А и В называются несовместными, если они не могут происходить одновременно, т.е., Р(АB)=0.

Набор событий А1, А2,…. Аk образует полную группу, если, во-первых, любые два из них несовместны:

и, во-вторых, одно из этих событий обязательно происходит, иначе говоря:

Условная вероятность события А при условии В есть

(в предположении, что Р(В)>0). Если событие А не зависит от события В, то

Таким образом, для независимых событий вероятность произведения событий P(AB) равна произведению их вероятностей:

Если события А1,…,Аn, P(Ai) > 0 образуют полную группу событий, то вероятность события В может быть представлена как сумма произведений безусловных вероятностей событий полной группы на условные вероятности события В (формула полной вероятности).

Случайные величины.

Если дана полная группа событий А1, А2, …Аk с вероятностями, i=1,2..k и набор чисел х1, х2,…хk, то случайной величиной называют некоторое значение, которое ставится в соответствие какому-либо событию. Непрерывная случайная величина Х - это величина, которая может принимать любые действительные значения. Дискретная случайная величина Х - это величина, принимающая значение хi , если происходит событие Аi (то есть, с вероятностью pi).

Несколько случайных величин называются одинаково распределенными, если их распределения совпадают (т.е. они принимают одинаковые значения с одинаковыми вероятностями). Как следствие, одинаково распределенные случайные величины имеют одинаковые средние и дисперсии (см. ниже).

Несколько случайных величин х1, х2, … хn называются независимыми, если вероятность того, что одновременно первая из них приняла значение с1, вторая - значение с2, n-ая - значение сn, совпадает с произведением вероятностей

каковы бы ни были числа с1, с2 , сn. Независимость можно понимать как отсутствие влияния результатов одних испытаний на другие.

Функции распределения.

Наиболее универсальный способ описания случайных величин заключается в отыскании их интегральных или дифференциальных функций распределения. Под интегральной функцией распределения результатов наблюдений понимается зависимость вероятности того, что результат наблюдения Xi в i-м опыте окажется меньшим некоторого текущего значения х, от самой величины х:

Поскольку функция распределения вероятности представляет собой вероятность, то она удовлетворяет следующим свойствам:

· ;

· - неубывающая функция от x;

· .

Более наглядным является описание свойств результатов наблюдений и случайных погрешностей с помощью дифференциальной функции распределения, иначе называемой плотностью распределения вероятностей:

Физический смысл f(x) состоит в том, что произведение f(x)dx представляет вероятность попадания случайной величины Х в интервал от х до х +dx, т.е.

От дифференциальной функции распределения легко перейти к интегральной путем интегрирования:

Размерность плотности распределения вероятностей, как это следует из формулы, имеет размерность обратную размерности измеряемой величины, поскольку сама вероятность - величина безразмерная.

Используя понятия функций распределения, легко получить выражения для вероятностей того, что результат наблюдений Х примет при проведении измерения некоторое значение в интервале [х1, х2].

В терминах интегральной функции распределения имеем:

т.е., вероятность попадания результата наблюдений или случайной погрешности в заданный интервал равна разности значений функции распределения на границах этого интервала, или площади, ограниченной кривой распределения, осью абсцисс и перпендикулярами к ней на границах этого интервала.

Для дискретной случайной величины соответствие между xi и pi выражается формулой

читаемой как «вероятность того, что Х принимает значение xi, равна рi». При этом

Набор пар {(xi,pi)} называется законом распределения, или просто распределением величины Х.

Для любого числа d можно определить вероятность того, что Х примет значение, не меньшее чем d:

Аналогично, для любых чисел с < d

Таким образом, интегрирование в случае дискретной случайной величины заменяется суммированием.

Числовые характеристики случайной величины.

Среди числовых характеристик случайных величин нужно, прежде всего, отметить те, которые характеризуют положение случайной величины на числовой оси, т.е. указывают некоторое среднее, ориентировочное значение, около которого группируются все возможные значения случайной величины.

Из характеристик положения в теории вероятностей важнейшую роль играет математическое ожидание случайной величины, которое иногда называют просто средним значением случайной величины.

Рассмотрим дискретную случайную величину X, имеющую возможные значения х1, х2, … хn, с вероятностями p1, р2, …, pn. Чтобы охарактеризовать каким-то числом положение значений случайной величины на оси абсцисс с учетом того, что эти значения имеют различные вероятности, можно воспользоваться так называемым «средним взвешенным» из значений хi, причем каждое значение хi при осреднении должно учитываться с «весом», пропорциональным вероятности этого значения. Таким образом, мы вычислим среднее значение случайной величины X, которое обозначим М[Х]:

Это среднее взвешенное значение, т.е., сумма произведений всех возможных значений случайной величины на вероятности этих значений, называется математическим ожиданием случайной величины.

Для непрерывной величины X математическое ожидание выражается не суммой, а интегралом:

Вместо обозначения M [X] для математического ожидания величины X в ряде случаев, когда величина М [Х] входит в формулы как определенное число, ее удобнее использовать обозначение в виде одной буквы. В этих случаях математическое ожидание величины X обозначается через mx:

Обозначения mx и М [Х] для математического ожидания применяются параллельно в зависимости от удобства той или иной записи формул.

Кроме характеристик положения - средних, типичных значений случайной величины - употребляется еще ряд характеристик, каждая из которых описывает то или иное свойство распределения.

Дисперсией D(X) случайной величины X называется число

Дисперсия случайной величины есть характеристика рассеивания (разбросанности) значений случайной величины около ее математического ожидания. Само слово «дисперсия» означает «рассеивание».

Дисперсия случайной величины имеет размерность квадрата случайной величины; для наглядной характеристики рассеивания удобнее пользоваться величиной, размерность которой совладает с размерностью самой случайной величины. Для этого из дисперсии извлекают квадратный корень. Полученная величина называется средним квадратическим отклонением (стандартом, или средним разбросом) случайной величины X и обозначается σ[X]. Для упрощения записей чаще используются сокращенные обозначения среднего квадратического отклонения и дисперсии - σx и Dx:

Математические ожидания и дисперсии обладают рядом полезных свойств. Так, если C - некоторое число, то случайная величина Y=X+C принимает значения хi + C с вероятностями pi и, следовательно,

Поэтому

При проведении системных расчетов обычно интересуются комбинациями переменных. Например, при расчетах времени ответа мы суммируем большое число различных переменных. При расчете времени доступа к файлу данных мы должны знать долю сообщений, направляемых к различным файлам. Использование дисперсии и второго момента упрощает манипуляции с комбинацией переменных.

Когда необходимо найти математическое ожидание и дисперсию случайной величины С, которая является суммой двух случайных величин А и В, то в этом случае

т.е., математическое ожидание суммы случайных величин равно сумме математических ожиданий каждой случайной величины, и дисперсия суммы случайных величин равно сумме дисперсий.

В общем случае, среднее значение суммы произвольного числа случайных величин равно сумме их средних:

Из свойств следует часто применяющаяся на практике формула вычисления дисперсии:

Весьма важным для использования в имитационном моделировании является коэффициент вариации, определяемый как отношение среднеквадратического отклонения случайной величины к ее математическому ожиданию: