6.6. Электронная цифровая подпись

 

Электронная цифровая подпись - это реквизит электронного документа, предназначенный для защиты данного электронного документа от подделки, полученный в результате криптографического преобразования информации с использованием закрытого ключа электронной цифровой подписи и позволяющий идентифицировать владельца сертификата ключа подписи, а также установить отсутствие искажения информации в электронном документе.

 

6.6.1.Основные операции с ЭЦП

 

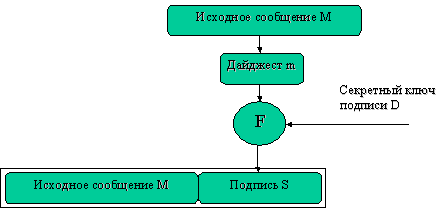
Общее правило создания ЭЦП:

От значения электронного документа M вычисляется его хэш-значение (или дайджест) m.

На вход алгоритма электронной цифровой подписи поступают значение дайджеста электронного документа и секретный ключ D подписывающего.

На выходе алгоритм F дает значение электронной цифровой подписи S, сделанной для документа M.

Значение электронной цифровой подписи S посылается вместе с текстом электронного документа M в одном информационном пакете.

 

 

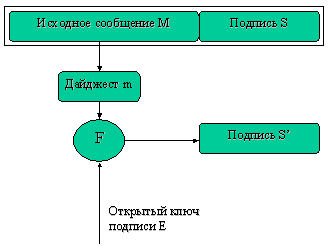
Общее правило верификации ЭЦП.

От значения принятого электронного документа M вычисляется его хэш-значение (или дайджест) m.

На вход алгоритма электронной цифровой подписи поступают значение дайджеста электронного документа и открытый ключ E автора подписи.

На выходе алгоритм F дает значение электронной цифровой подписи S`, сделанной для документа M.

Полученное значение S` сравнивается с принятым значением S. Если эти значения совпадают, то процедура верификации прошла успешно.

Анализ результатов верификации ЭЦП.

Если процедура верификации дала положительный результат, то это означает, что документ, для которого была вычислена ЭЦП, не был изменен и авторство документа подтверждено. 

Если процедура верификации дала отрицательный результат, т.е. значения принятой и вычисленной подписей не совпадают, то возможны следующие ситуации:

В электронный документ были внесены несанкционированные изменения.

Подпись для электронного документа была подделана.

Автором документа является другой абонент.

Если процедура верификации дала отрицательный результат, то авторство, подлинность и целостность электронного документа не могут быть гарантированы.

 

6.6.2.Математические основы криптографии на эллиптических кривых

 

Использование эллиптических кривых для криптографии было независимо предложено Нилом Коблицем (Neal Koblitz) и Виктором Миллером (Victor Miller) в середине 80-х годов прошлого века [Kob87, Mil85]. На сегодняшний день это одно из самых перспективных направлений развития криптографии с открытыми ключами.

Эллиптической кривой , определенной в конечном поле , где , называется множество точек с координатами , удовлетворяющих уравнению:

,

где  и  вместе со специальной точкой , называемой точкой бесконечности или, как еще иногда говорят, нулевой точкой [Коб2001]. В группе точек на эллиптической кривой точка бесконечности  нужна для обеспечения существования обратного элемента в группе и необходимых свойств операций.

Рассмотрим основные операции над точками и их геометрическую интерпретацию на примере обычных плоских эллиптических кривых, т.е. кривых определенных над полем вещественных чисел. Полученные в результате аналитические формулы для рассматриваемых операций являются действительными для эллиптических кривых (5.1), определенных над любым полем.

Точкой, обратной к данной точке , называется точка с координатами  и обозначается как , т.е. точка, зеркально отраженная от оси абсцисс.

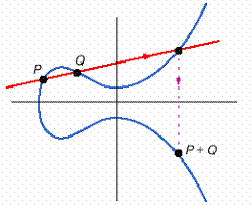
Геометрический смысл операции сложения двух точек  на эллиптической кривой (рис.NN) заключается в том, что через них проводится секущая, пересекающая кривую в третьей точке. Обратная точка для точки пересечения дает результат операции сложения.

 

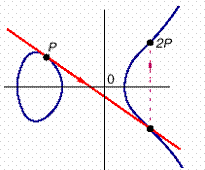
Если некоторая точка эллиптической кривой  складывается сама с собой (рис.5.2), то такая процедура называется удвоением точки. Геометрический смысл подобной операции заключается в том, что через точку  проводится секущая линия, которая пересекает кривую в некоторой точке. Обратная точка к точке пересечения и будет результатом удвоения точки .

Операции сложения и удвоения точек имеют аналитические выражения.

Сложение точек. Пусть  – две точки, для которых . Тогда ,где

,

,

и

.

Удвоение точки. Пусть точка , для которой y1  0 (если , тогда , т.е. ), тогда , где

,

,

и

.

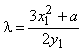Точка бесконечности. Геометрический смысл точки бесконечности заключается в том, что в ней пересекаются все прямые, параллельные оси ординат. Рассмотрим операции с участием точки бесконечности  и некоторой точки :

1) ;

2) ;

3) .

 

Количество точек, принадлежащих эллиптической кривой называется рангом кривой и обозначается буквой . Рангом точки называется такое минимальное целое положительное число , что . Ранг точки определяет порядок группы точек эллиптической кривой, с которыми осуществляются криптографические преобразования.

Операция сложения двух точек, принадлежащих эллиптической кривой, определенной на конечном поле, является аналогом операции умножения двух чисел в конечном поле. Операция умножения точки на некоторое число  является аналогом операции возведения в степень . Операцию умножения точки на число можно представить как процесс сложения точки самой с собой нужное число раз. Например:

,

 и т.д.

Однако существует способ быстрого умножения точки на число, который требует  количества операций для умножения точки , определенной в конечном поле  на некоторое число . Этот метод аналогичен алгоритму быстрого возведения в степень для элементов конечного поля, действительно: .

В группе точек, принадлежащих эллиптической кривой существует задача, имеющая экспоненциальный уровень сложности и получившая название задачи дискретного логарифмирования на эллиптической кривой. Суть ее заключается в том, что при известных точках , вычислительно трудно найти такое число  (если оно существует), что . Надежность криптографических систем на эллиптических кривых основана на сложности решения этой задачи. Приведем оценки необходимой вычислительной мощности для нахождения дискретного логарифма в группе точек эллиптической кривой [Jon01]:

 

Задача дискретного логарифмирования в группе точек эллиптической кривой является более трудной, чем задача дискретного логарифмирования в конечном поле. В этом заключается основная причина преимущества использования криптосистем на эллиптических кривых, которые обеспечивают такой же уровень стойкости при использовании чисел существенно меньшего размера по сравнению с более традиционными криптосистемами, надежность которых заключается в сложности задачи факторизации или дискретного логарифмирования в конечном поле. Соответственно при использовании чисел одинаковой размерности уровень стойкости криптосистем на эллиптических кривых значительно выше. На сегодняшний день лучший из известных алгоритмов – -метод Полларда, дает следующую оценку для решения задачи дискретного логарифмирования в группе точек эллиптической кривой: , где  – количество процессоров для параллельных вычислений, а  – порядок группы точек эллиптической кривой [Esc99]. С помощью этого метода в 2000 г. была решена задача дискретного логарифмирования в группе точек эллиптической кривой с порядком в 108 бит. В 2002 году была решена задача для эллиптической кривой с порядком в 109 бит. Для сравнения отметим, что криптосистема, использующая преобразования в группе точек эллиптической кривой с порядком в 160 бит, эквивалентна по стойкости криптосистеме RSA с модулем шифрования в 1024 бита.

 

6.6.3.Стандарт ГОСТ Р 34.10-2001

 

Стандарт ГОСТ Р 34.10-2001 является отечественным стандартом на алгоритм электронной цифровой подписи. Алгоритм относится к классу криптографических алгоритмов с открытыми ключами и основан на использовании преобразований в группе точек на эллиптической кривой, определенной в конечном поле [ГОСТ01]. Стандарт принят в 2001 году и введен в действие с июля 2002 года. Стандарт определяет процессы формирования и проверки ЭЦП. Новый отечественный стандарт ГОСТ Р 34.10-2001 совместим с соответствующими международными стандартами ИСО в области защиты информации, механизмов формирования ЭЦП и управления сертификатами. Новый алгоритм ЭЦП обладает большим уровнем стойкости  по сравнению с алгоритмом, определенным в старом стандарте ГОСТ Р 34.10-94. Стойкость алгоритма основана на сложности решения задачи дискретного логарифмирования в группе точек на эллиптической кривой и на стойкости используемой хэш-функции. В качестве хэш-функции используется отечественный стандарт ГОСТ Р 34.11-94. Рекомендуется применять новый стандарт при разработке новых систем и приложений, а также при модификации уже существующих решений. Значение цифровой подписи, поучаемое в результате выполнения алгоритма, представляет собой двоичную последовательность, длинной 512 бит. Модулем эллиптической кривой, используемым при формировании подписи, является число p>2255. Значение порядка циклической подгруппы группы точек на эллиптической кривой лежит в интервале от 2254 до 2256.

 

Ниже приводится подробная структура алгоритма:

 

Генерация ключей:

Выбирается простое число  такое, что p>2255, являющееся модулем эллиптической кривой. Выбираются такие коэффициенты  и  эллиптической кривой  вида

,

что

,

   и   .

Пусть  – порядок группы точек эллиптической кривой.

Выбирается точка , ранг которой равен , т.е. . При этом для числа  должны выполнятся следующие условия:

                                 простое число;  

                                

         , где  

Выбирается некоторое число d, удовлетворяющее условию:

.

Вычисляется точка .

открытый ключ подписи: ;

секретный ключ подписи:.

 

Подпись сообщения:

Пусть  – сообщение, для которого нужно вычислить значение электронной цифровой подписи;  – функция хеширования.

Определяется такое значение , что

,

если , то берется .

Генерируется случайное целое число , удовлетворяющее условию:

.

Вычисляется точка  с координатами .

Далее определяется такое значение , что

,

если , то необходимо сгенерировать другое значение числа  и повторить вычисление значения .

Вычисляется такое значение , что

,

если , то также необходимо заново сгенерировать значение числа  и повторить вычисления.

Значение ЭЦП: пара чисел  являются электронной цифровой подписью для сообщения .

 

Верификация (проверка цифровой подписи):

Вычисляется такое значение , что

,

если , то берется .

Вычисляется такое значение , что

.

Вычисляются два таких значения  и , что

,

.

Вычисляется такая точка эллиптической кривой , что

.

Вычисляется такое значение , что

.

Если значение , то процедура верификации прошла успешно и подпись считается верной. В противном случае подпись не принимается.

Рассмотрим конкретный пример вычисления и проверки ЭЦП. В примере показаны вычисления для чисел небольшого размера. В связи с этим используются некоторые упрощения условий, накладываемых на стандарт.

 

Генерация параметров:

Пусть модуль эллиптической кривой = 1021

Пусть коэффициенты эллиптической кривой  = 1,  = 1.

Выберем точку  = (752, 453) , принадлежащую кривой.

Число q=521 является рангом точки P.

Случайным образом выбираем уникальное число d. Пусть  = 111.

Вычисляем значение точки :

(752, 453) * 111 = (272, 824)

Имеем = (272, 824)

Подпись сообщения:

Пусть числовой формой исходного сообщения является число m=240

Случайным образом выбираем число k

Пусть = 211.

Вычисляем значение точки

 (752, 453) * 211 = (787, 220)

Имеем С  = (787, 220)

Координата x точки С равна 787

Определяем число

 = 787 mod 521= 266,

Определяем число

= (240*211 + 111*266) mod 521 = 453.

Имеем s = 453

Подпись для сообщения m: ( = 266,  = 453).

 

Проверка подписи сообщения:

Вычисляем необходимые значения:

=  = (1/240) mod 521 = 432

Имеем v = 432

z1 = 453 * 432 mod 521 = 321.

Имеем z1=321

z2 = ((0-266) mod  * 432) mod 521 = 229.

Имеем z2=229

= (683, 384) + (864, 236) = (787, 220).

Вычисляем значение R

R = 787 mod 521 = 266.

Имеем = 266 = .

Процедура верификации прошла успешно. Подпись верна.

 

6.6.4.Алгоритм ECDSA

 

Алгоритм ECDSA (Elliptic Curve Digital Signature Algorithm) определяет правила формирования и проверки электронной цифровой подписи. Также как и стандарт ГОСТ Р 34.10-2001, он основан на использовании криптографии на эллиптических кривых. Алгоритм ECDSA входит в состав стандартов ANSI X9.62, IEEE P1363, ISO 14888-3-99, а также является стандартом электронной цифровой подписи в США под кодом FIPS 186-2. Ожидается, что этот стандарт должен заменить собой предыдущий стандарт DSA.

 

6.6.5.Стандарты ГОСТ Р 34.10-94 и DSA

 

Данные стандарты являются предыдущими версиями соответственно отечественного и американского стандартов на алгоритмы электронной цифровой подписи. Эти алгоритмы имеют схожую структуру и отличаются только незначительными вариациями в формулах для вычисления подписи и ее верификации. Стойкость алгоритмов основана на сложности решения задачи дискретного логарифмирования в конечном поле.

 

 

К оглавлению

Назад к разделу "6.5. Алгоритмы с открытыми ключами"

Вперед к разделу "6.7. Защита электронных транзакций"