11.  Сети массового обслуживания

(к оглавлению)

 

Цель работы:

Изучение моделей экспоненциальных сетей массового обслуживания и методов расчета их локальных и интегрированных показателей.

 

Теоретические сведения

 

Сеть массового обслуживания (СеМО) представляет собой совокупность конечного числа взаимосвязанных узлов обслуживания, в которой циркулируют заявки, переходящие в соответствии с маршрутной матрицей с выхода одного узла на вход другого. Каждый отдельный узел является разомкнутой СМО и отображает функционально самостоятельную часть реальной системы.

СеМО используются для определения таких важных характеристик моделируемых систем как:

-   производительность;

-   время доставки заявок (сообщений, пакетов и пр.);

-   вероятность потери заявки;

-   вероятность блокировки узла;

-   допустимые значения нагрузки, при которых обеспечивается требуемое качество обслуживания

и др.

 

Для наглядного представления СеМО используется граф, вершины которого (узлы) соответствуют отдельным узлам сети, а дуги отображают связи между узлами.

Переход заявок между узлами происходит мгновенно в соответствии с переходными вероятностями , обозначающими вероятность того, что заявка после обслуживания в узле i перейдет в узел j.

Если узлы i и j непосредственно между собой не связаны, то  = 0.

Если из узла i возможен переход только в узел j, то  = 1.

Под входным потоком некоторого узла будем понимать поток заявок, приходящих на вход этого узла из внешней среды. В общем случае число входных потоков СеМО равно числу образующих сеть узлов.

Наиболее разработанной является теория экспоненциальных СеМО, основанная на аппарате марковских процессов с непрерывным временем, с помощью которой можно получить аналитические выражения для нахождения основных показателей исследуемых систем.

Экспоненциальной называют сеть, обладающую следующими свойствами:

-   входные потоки пуассоновские;

-   время обслуживания заявок в узлах распределено по экспоненциальному закону;

-   заявки в узлах обслуживаются в порядке поступления;

-   переход заявки с выхода i-го узла на вход j-го узла является независимым случайным событием, имеющим вероятность ,  - вероятность ухода заявки из CeМО.

 

Из этих свойств следует, что время обслуживания в каждом узле не зависит ни от времени обслуживания в других узлах, ни от параметров входящего потока, ни от состояния сети, ни от маршрутов следования требований.

Чтобы задать разомкнутую экспоненциальную СеМО необходимо задать значения следующего набора параметров:

-   число узлов N;

-   число каналов i-ого узла ;

-   матрицу вероятностей передач ;

-   интенсивности входных потоков заявок ;

-   интенсивности  или средние времена  обслуживания заявок в узлах .

 

Интенсивности входных потоков в узлах λ1,..., λN находятся из уравнений баланса сети (см.далее) с учетом свойств слияния и разветвления потоков.

Стационарность сети означает, что среднее число заявок в любом ее фрагменте неизменно, т.е., суммарная интенсивность входящих в эту часть потоков равна суммарной интенсивности выходящих. Математическая запись этого факта называется уравнением баланса. Если в качестве фрагментов сети взять ее узлы, то, составляя уравнения баланса для каждого узла, можно получить систему уравнений, связывающую неизвестные интенсивности λ1,..., λN c известными Λ1,.., ΛN. В этом случае для N неизвестных получаются N уравнений. Добавлением к ним уравнения баланса для входных и выходных потоков всей сети в целом, получается система из N+1 уравнений, одно из которых можно использовать для проверки.

Сеть стационарна, если стационарны все ее узлы, т.е. если

 

 (11‑1)

где

 

Поток заявок на входе отдельного узла складывается из входного потока сети (возможно, нулевой интенсивности) и из потоков, поступающих с выходов других узлов. Входной поток узла в экспоненциальной сети в общем случае пуассоновским не является, поэтому узлы СеМО в общем случае не экспоненциальные. Тем не менее, узлы все же часто считают экспоненциальными. Это позволяет найти из уравнений баланса значения интенсивностей λ1,..., λN входных потоков заявок и воспользоваться для расчета показателей сети соответствующими аналитическими моделями теории МО.

Помимо показателей отдельных узлов для описания сети используются показатели, отражающие свойства сети в целом. К наиболее важным относятся следующие.

-   Среднее время пребывания заявки в сети.

Время пребывания заявки в сети определяется как время, прошедшее с момента прихода заявки в сеть до момента ее ухода из сети. Среднее время пребывания рассчитывается по формуле:

 

 (11‑2)

где Λ = Λ1+...+ΛN,

 - среднее время пребывания заявки в j-ом узле (см. п.? раздела).

-   Передаточные коэффициенты.

Под передаточным коэффициентом понимается среднее значение числа приходов  заявки i-го входного потока в j-ый узел за время пребывания этой заявки в сети.

В стационарном режиме при любых Λ1,...ΛN для λ1,...λN справедливо:

 

 (11‑3)

 

Интенсивности прихода заявок в j-ый узел λ1, λ2… λN выражены в (11‑3) через интенсивности входных потоков сети Λ1,... ΛN.

Суммы в правой части (11‑3) можно рассматривать как элементы матрицы-строки, представляющей собой произведение вектор-строки  =Λ1,...ΛN на матрицу . Таким образом, (11‑3) можно записать в матричном виде:

 

 

где  - вектор-строка λ1,...λN.

 

Положив в (11‑3) Λ1 = 1 и Λ2 = ... = ΛN = 0, получим

 

 (11‑4)

 

т.е., строку коэффициентов  - матрицы  можно найти, решив уравнения баланса сети при Λ1=1, Λ2 = ... = ΛN = 0: согласно (11‑4), найденные значения λ1,..., λN будут численно равны коэффициентам ,... .

Значения ,...,  находятся как решение уравнений баланса для Λk=1 и Λi = 0, i≠k.

Таким образом, находим последовательно значения элементов всех строк матрицы .

-   Средние входовые времена пребывания в сети.

Средним входовым временем пребывания в сети  называется среднее время пребывания в сети заявки, поступающей из i-го входного потока, .

Показатели  можно вычислить по формуле:

 

 (11‑5)

 

-   Абсолютные пропускные способности.

Абсолютную пропускную способность по i-му входу Ai можно найти непосредственно по ее определению.

Записав условие стационарности СеМО в виде:

 

что эквивалентно

 

и выражая λi через Λi из (11‑3), получим развернутую форму условия стационарности:

 

 (11‑6)

 

Некоторые из неравенств (11‑6) оказываются излишними: такие неравенства можно исключать из (11‑6), не изменяя решения системы.

Если все входные интенсивности сети, кроме Λi, положить равными нулю, то, используя развернутую форму записи условий стационарности, получим, что для стационарности необходимо, чтобы

 

или

 (11‑7)

 

Величина Ai определится как минимум значений, стоящих в правых частях неравенств (11‑7):

-   Условные пропускные способности.

Условной пропускной способностью по i-му входу Bi называют максимальное значение интенсивности Λi, при котором сеть остается стационарной.

При заданных Λk (k≠i) сеть стационарна для любых значений .

Условная пропускная способность, как и абсолютная, может быть найдена из (11‑3). Для нахождения Bi в (11‑3) следует подставить значения всех входных интенсивностей сети, кроме Λi и разрешить полученную систему относительно Λi:

 (11‑8)

 

Bi находится как наименьшая из правых частой в (11‑8).

-   Запасы по пропускным способностям.

Запас по пропускным способностям , показывает, насколько может быть увеличена интенсивность прихода заявок на i-ом входе при фиксированных остальных без нарушения условия стационарности.

 

Содержание работы.

Для экспоненциальной разомкнутой сети массового обслуживания требуется рассчитать:

1. Частные характеристики узлов СеМО.

2. Среднее время пребывания заявки в сети. Для узлов сети с интенсивностями входного потока Λi> 0.

3. Среднее входовое время пребывания заявки в сети.

4. Абсолютную пропускную способность.

5. Условную пропускную способность.

6. Запас по пропускной способности.

 

Конфигурация сети составляется по описанию, приведенному в разделе 0 в соответствии с номером варианта.

Номер варианта определяется по правилу:

<Номер в списке группы> mod10

 

Отчет по работе:

Отчет по работе должен включать исходные данные и результаты расчетов.

Контрольные вопросы:

1)Дайте определение сети массового обслуживания.

2)Какие сети МО называют экспоненциальными?

3)Что задают переходные вероятности?

4)Что называется передаточным коэффициентом?

5)Что выражает уравнение баланса? Сколько уравнений баланса можно составить для одной СМО?

6)Как определяется среднее время пребывания заявки в сети? Каким образом можно найти среднее время пребывания заявки в сети?

7)Запишите развернутую форму условия стационарности СеМО.

8)Что понимается под средними входовыми временами? Как они рассчитываются?

9)Как можно найти абсолютные пропускные способности?

10)Как можно найти относительные пропускные способности?

11)Что показывает запас по пропускной способности?

 

Варианты

 

Индивидуальный вариант сети составляется преобразованием показанного на рисунке варианта.

 

 

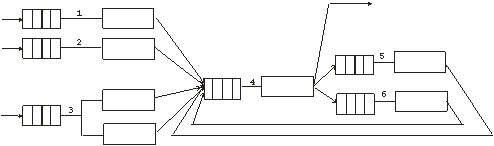
путём удаления из него некоторых узлов.

 

Удаляемые узлы указаны в таблице вариантов знаком “ - ”,

Остающиеся узлы указаны в таблице вариантов знаком “ + ”.

 

 

Правила удаления узлов:

-   Если удаляется узел с номером от 1 до 3, то удаляется также соответствующий входной поток. Например, при удалении СМО 1 удаляется поток с интенсивностью Λ1.

-   Если удаляется узел 5 или узел 6, то величина р40 увеличивается соответственно на величину р45 (т.е. на 0,5) или р46 (т.е. на 0,2).
Например, при удалении узла 5 величина р40 увеличивается на 0,5 и будет равна 0,8.

-   После удаления какого-либо узла оставшиеся узлы нумеруются заново.

 

Значения параметров:

Число узлов N = 6

Число каналов в узлах:

n1=1,

n2=1,

n3=2,

n4=1,

n5=1,

n6=1.

 

Переходные вероятности

р40 =0,3,

р45 = 0,5,

р46= 0,2.

 

Интенсивности входящих потоков (заявок в секунду)

Λ1 = 1/100,

Λ2 = 1/70,

Λ3= 1/50.

 

Среднее время обслуживания в узлах (секунд)

 ,

 ,

 ,

 ,

 ,

 .