10. Замкнутая СМО

(к оглавлению)

Рассмотрим СМО, в которых источник требований является внутренним и генерирует ограниченный поток заявок общим числом r. Интенсивность входящего потока заявок зависит, таким образом, от состояния системы. Например, ремонтное подразделение производственного предприятия, состоящее из n механиков, отвечает за обслуживание парка станков, состоящего из r единиц, r>n, причем каждый станок может обслуживаться только одним механиком. Суммарная интенсивность входящего потока зависит от того, сколько в данный момент неисправных станков k ремонтируется или стоит в очереди на ремонт и сколько станков находится в эксплуатации (r - k). Источником входящего потока требований являются станки, находящиеся в эксплуатации (r - k), которые в случайные моменты времени выходят из строя и требуют обслуживания.

Общий входящий поток имеет интенсивность:

Λ= (r - k) λ.

Требование, поступившее в систему в момент, когда свободен хотя бы один канал, немедленно направляется на обслуживание.

Если требование застает все каналы занятыми обслуживанием других требований, оно не покидает систему, а становится в очередь и ждет, пока один из каналов не станет свободным. Максимальная длина очереди, таким образом, равна r‑n, входящий поток требований формируется выходящим потоком.

Если λ - интенсивность потока требований в расчете на один объект, то:

Решение системы алгебраических уравнений для стационарного режима СМО относительно имеет вид:

(0‑1)

Другие показатели СМО определяются из выражений:

- Среднее число требований в очереди на обслуживание

(0‑2)

- Среднее время ожидания в очереди

(0‑3)

- Среднее число занятых каналов

(0‑4)

- Среднее число простаивающих объектов (находящихся на обслуживании и в очереди)

(0‑5)

- Коэффициент простоя объектов

(0‑6)

- Коэффициент использования объектов

(0‑7)

- Коэффициент нахождения объектов в очереди

(0‑8)

- Коэффициент загрузки каналов

(0‑9)

Содержание работы.

Подготовка инструментария эксперимента.

Выполняется в соответствии с общими правилами.

Расчет на аналитической модели.

1)В приложении Microsoft Excel подготовьте таблицу следующей структуры (по причине большой ширины таблицы левая, центральная и правая ее части по горизонтали показаны на отдельных рисунках).

2)Параметры СМО заносятся в столбцы:

r: число объектов

n: число каналов

Ta: средний интервал между приходами объектов на обслуживание

Ts: среднее время обслуживания объектов

Значение полагается равным порядковому номеру в списке группы.

Значения r, n и полагаются равными соответственно:

r=6

n=1,2,3

Таким образом, необходимо найти теоретические и экспериментальные значения показателей СМО для 15 комбинаций значений параметров.

3)В столбцах r и b части Аналитическая модель запишите выражения для вычисления промежуточных и конечных результатов:

r: Ts / Ta

1: Коэффициент перед P1 (0‑1)

2: Коэффициент перед P2 (0‑1)

… ………………..

6: Коэффициент перед P6 (0‑1)

P0: Выражение для P0 (0‑1)

P1: Выражение для P1 (0‑1)

… …………

P6: Выражение для P6 (0‑1)

S: (контрольная сумма)

nw: Выражение для средней длины очереди (0‑2)

ns: Выражение для среднего числа занятых каналов (0‑4)

c: Выражение для коэффициента загрузки канала (0‑9)

4)В столбцы правой части таблицы (Имитационная модель) заносятся результаты, полученные на программной модели.

Эксперимент на имитационной модели.

1)Установите режим запусков с экспоненциально распределенным временем рабочего состоянии и экспоненциально распределенным временем восстановления (обслуживания), задав значение соответствующих параметров.

2)Для каждой комбинации r, n, Ta, Ts осуществите запуск модели.

3)Результаты запусков внесите в таблицу.

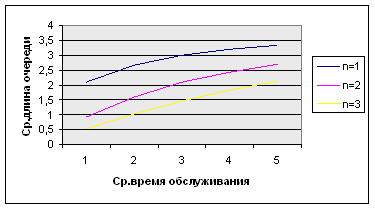
4)Для каждой комбинации r, n, Ta постройте график зависимости nw= F(Ts).

Анализ результатов.

1)Проанализируйте результаты, полученные теоретическим и экспериментальным способами, сравните результаты между собой.

Отчет по работе:

Отчет по работе должен включать:

- исходные данные,

- результаты расчетов,

- результаты экспериментов с программной моделью,

- графики nw= F(Ts).

Контрольные вопросы:

1)Дайте краткое описание замкнутой модели СМО.

2)При каких условиях в замкнутой СМО устанавливается стационарный режим?

Задачи.

1)Проведите эксперимент для тех же наборов значений параметров для дисциплины обслуживания с приоритетами для коротких заявок.

2)Исследуйте зависимость системных показателей от вида распределения времени обслуживания.

3)Проведите исследование экономической эффективности выбора значений параметров СМО (в соответствии с перечнем в п.0), для чего постройте таблицу со структурой:

(Левая часть)

(Правая часть)

Найдите значения прибыли в единицу времени при различных сочетаниях параметров.

Постройте графики зависимости прибыли от числа каналов при фиксированных временных параметрах.