7. Многоканальная СМО с ограниченной очередью

(к оглавлению)

 

Цель работы:

Овладение аналитическими методами и методами имитационного моделирования исследования многоканальных систем массового обслуживания с ограниченной очередью заявок.

 

Теоретические сведения

 

Рассмотрим n-канальную систему массового обслуживания с ожиданием.

Будем считать входящий поток заявок на обслуживание простейшим потоком с интенсивностью λ.

Интенсивность потока обслуживания равна μ. Длительность обслуживания – случайная величина, подчиненная показательному закону распределения. Поток обслуживаний является простейшим пуассоновским потоком событий.

Размер очереди допускает нахождение в ней m заявок.

Для нахождения предельных вероятностей можно использовать следующие выражения.

 

 (0‑1)

 

где .

 

Вероятность отказа в обслуживании заявки (отказ произойдет в случае, если все каналы заняты и в очереди находятся m заявок):

 

 (0‑2)

 

Относительная пропускная способность.

 

 (0‑3)

 

Абсолютная пропускная способность.

 

 (0‑4)

 

Среднее число занятых каналов.

Для СМО с очередью среднее число занятых каналов не совпадает (в отличие от СМО с отказами) со средним числом заявок в системе. Отличие равно числу заявок, ожидающих в очереди.

Обозначим среднее число занятых каналов . Каждый занятый канал обслуживает в среднем μ заявок в единицу времени, а СМО в целом – А заявок в единицу времени. Разделив А на μ получим

 

 (0‑5)

 

Среднее число находящихся в очереди заявок.

Для нахождения среднего числа ожидающих в очереди заявок в случае, если χ≠1, можно использовать выражение:

 

 (0‑6)

 

Для χ=1 необходимо подсчитать сумму:

 

 (0‑7)

где  = .

 

Среднее число находящихся в системе заявок.

 

 (0‑8)

 

Среднее время ожидания заявки в очереди.

Среднее время ожидания заявки в очереди можно найти из выражения (χ≠1).

 

 (0‑9)

 

Среднее время пребывания заявки в системе.

Так же как и в случае с одноканальной СМО имеем:

 

 (0‑10)

 

Содержание работы.

Подготовка инструментария эксперимента.

Выполняется в соответствии с общими правилами.

 

Расчет на аналитической модели.

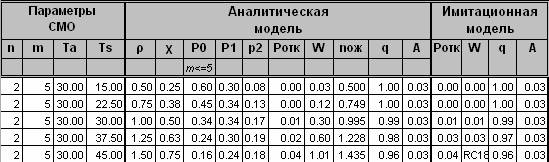
1. В приложение Microsoft Excel подготовьте таблицу следующего вида.

 

 

2. В столбцах для параметров СМО таблицы запишите свои исходные данные, которые определяются по правилу:

n=1,2,3

m=1,3,5

 

Для каждой комбинации {n,m} необходимо найти теоретические и экспериментальные значения показателей СМО для таких пар значений:

 = <порядковый номер в списке группы>

 

3. В столбцы с показателями аналитической модели впишите соответствующие формулы.

 

Эксперимент на имитационной модели.

1. Установите режим запусков с экспоненциально распределенным временем обслуживания, задав значение соответствующего параметра равным 1.

2. Для каждой комбинации n, m,  и  осуществите запуск модели.

Результаты запусков внесите в таблицу.

3. Внесите в соответствующие столбцы таблицы формулы для расчета среднего значения показателя Pотк, q и А.

 

 

Анализ результатов.

1. Проанализируйте результаты, полученные теоретическим и экспериментальным способами, сравнив результаты между собой.

2. Для одной из комбинаций {n,m} постройте на одной диаграмме графики зависимости Pотк от  на теоретически и экспериментально полученных данных.

 

Оптимизация параметров СМО.

Решите задачу оптимизации размера числа мест в очереди m для двух приборов со средним временем обслуживания  =  с точки зрения получения максимальной прибыли. В качестве условий задачи возьмите:

-   доход от обслуживания одной заявки равным 80у.е./час,

-   стоимость содержания одного прибора - 1у.е./час,

-   стоимость содержания одного места в очереди – 0.2у.е./час.

 

1. Для расчетов целесообразно создать таблицу:

 

 

Первый столбец заполняется значениями числа приборов n=1.

Второй столбец заполняется значениями чисел натурального ряда (1,2,3…).

Все клетки третьего и четвертого столбцов заполняются значениями .

В клетки столбцов с пятого по четырнадцатый переносятся формулы для столбцов таблицы раздела 0.

В столбцы с исходными данными разделов Доход, Расход, Прибыль внесите значения (см. выше).

В столбцах с вычисляемыми значениями разделов Доход, Расход, Прибыль запишите расчетные формулы:

- число заявок в единицу времени

Nr=A

- суммарный доход в единицу времени

IS= Ir*Nr

- суммарный расход в единицу времени

ES=Es*n + Eq*m

- прибыль в единицу времени

P= IS- ES

 

где

-    Ir - доход от одной заявки,

-    Es - расход на один прибор,

-    Eq - расход на одно место в очереди

 

2. Заполните строки таблицы для n=2 и n=3.

 

 

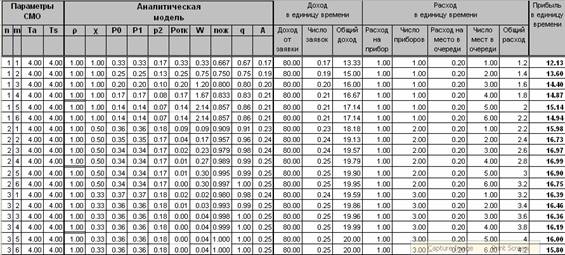
Найдите mопт для n=1,2,3.

 

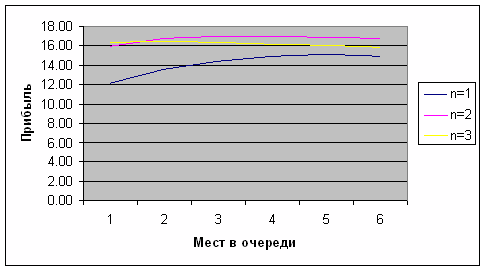
3. Постройте на одной диаграмме графики зависимости C(m) для n=1,2,3.

 

 

Отчет по работе:

Отчет по работе должен включать:

-   исходные данные,

-   результаты расчетов и экспериментов с программной моделью,

-   графики для Pотк,

-   таблицу с данными для нахождения наилучшего m и значение mопт,

-   графики зависимости прибыли в единицу времени от m для n=1,2,3.

 

Контрольные вопросы:

1)Дайте краткое описание многоканальной модели СМО с ограниченной очередью.

2)Какими показателями характеризуется функционирование многоканальной СМО с ограниченной очередью?

3)Как рассчитываются предельные вероятности многоканальной СМО с ограниченной очередью?

4)Как найти вероятность отказа обслуживания заявки?

5)Как найти относительную пропускную способность?

6)Чему равна абсолютная пропускная способность?

7)Как подсчитывается среднее число заявок в системе?

8)Приведите примеры многоканальной СМО с ограниченной очередью.

 

Задачи.

1)На автозаправочной станции установлены 3 колонки и площадка на 3 автомобиля для ожидания заправки. В среднем на станцию прибывает одна машина каждые 4 минуты. Среднее время обслуживания одной машины - 2,8 мин. Определить характеристики работы автозаправочной станции.

2)На станцию технического осмотра автомобилей, имеющего 3 смотровых поста, в среднем поступает 1 автомобиль за 0,4 часа. Стоянка во дворе вмещает 3 машины. Среднее время работы одного поста - 0,5 часа. Определить характеристики работы СТО.

3)В магазин осуществляется завоз товаров автомобилями. В течение дня прибывают в среднем 6 машин. Подсобные помещения для подготовки товаров к продаже позволяют обрабатывать и хранить товар, привезенный двумя машинами. В магазине работают посменно три фасовщика товаров, каждый из которых в среднем может обрабатывать товар одной машины в течение 5 часов. Продолжительность рабочего дня фасовщиков составляет 12 часов. Определить характеристики работы магазина, а также, какова должна быть емкость подсобных помещений, чтобы вероятность полной обработки товаров была больше 0,96.

4)В магазине работают три кассы. Среднее время обслуживания одного покупателя - 3 мин. Интенсивность потока покупателей - 7 человек в минуту. Число покупателей, стоящих в очереди к кассе, не может превышать 5 человек. Покупатель, пришедший в магазин, в котором в каждой очереди в кассу 5 человек, не ждет, а уходит из магазина. Определить характеристики работы магазина.

5)Оптовый склад производит отпуск товаров клиентам. Погрузку автомашины осуществляют три бригады грузчиков, каждая из которых состоит из 4 человек. Склад одновременно вмещает 5 автомашин и, если в это время прибывает новая автомашина, то она не обслуживается. Интенсивность входящего потока составляет 5 автомашин в час. Интенсивность по грузки составляет 2 автомашины в час. Дайте оценку работы склада и вариант его реорганизации.

6)Таможня располагает тремя терминалами. Интенсивность потока автомашин, перевозящих грузы и подлежащих прохождению таможенного контроля, составляет 30 шт. в сутки. Среднее время таможенной обработки на терминале одной автомашины составляет 3 часа. Если в очереди на прохождение таможенного контроля стоят 5 автомашин, то приезжающие автомашины уезжают на другую таможню. Найти показатели эффективности работы таможни.

7)На строительную площадку в среднем через 40 мин прибывают автомашины со строительным материалом. Среднее время разгрузки одной автомашины составляет 1,8 часа. В разгрузке принимают участие две бригады грузчиков. На территории строительной площадки может находиться в очереди на разгрузку не более 5 автомашин. Определить показатели эффективности работы строительной площадки.

8)На мойку, имеющую три рабочих места, в среднем в час приезжает 12 автомашин. Если в очереди уже находится 6 автомашин, вновь приезжающие автомобили не встают в очередь, а покидают мойку. Среднее время мойки автомашины составляет 20 мин, средняя стоимость услуг мойки - 150 руб. Определить показатели эффективности работы мойки и среднюю величину потери выручки в течение рабочего дня (с 9 до 19 часов).

9)Интенсивность потока автомашин, перевозящих грузы и подлежащих прохождению таможенного контроля, составляет 50 шт. в сутки. Среднее время таможенной обработки на терминале одной автомашины составляет 2,8 часа. Максимальная очередь на прохождение таможенного контроля должна быть не более 8 автомашин. Определить, какое количество терминалов надо открыть на таможне, чтобы вероятность простоя автомашин была минимальна.