6. Одноканальная СМО с ограниченной очередью
(к оглавлению)
Цель работы:
Овладение аналитическими методами и методами имитационного моделирования исследования одноканальных систем массового обслуживания с ограниченной очередью заявок.
Теоретические сведения
Рассмотрим одноканальную систему массового обслуживания с ожиданием.
Будем предполагать, что входящий поток заявок на обслуживание есть простейший поток с интенсивностью λ.
Интенсивность потока обслуживания равна μ. Длительность обслуживания – случайная величина, подчиненная показательному закону распределения. Поток обслуживаний является простейшим пуассоновским потоком событий.
Заявка, поступившая в момент, когда канал занят, становится в очередь и ожидает обслуживания. Будем считать, что размер очереди ограничен и не может вместить более m заявок, т.е. заявка, заставшая в момент своего прихода в СМО m+1 заявок (m ожидающих в очереди и одну, находящуюся на обслуживании), покидает СМО.
Система уравнений, описывающих процесс в этой системе, имеет решение:
(0‑1)
Знаменатель первого выражения представляет собой геометрическую прогрессию с первым членом 1 и знаменателем ρ, откуда получаем
и предельные вероятности приобретают вид:
(0‑3)
………………
Выполнение условия стационарности ρ < 1 необязательно, поскольку число заявок в СМО контролируется путем введения ограничения на длину очереди. Однако выражение справедливо только при ρ<1 (поскольку для ρ =1 получается неопределенность вида 0/0). Сумма геометрической прогрессии со знаменателем ρ = 1 равна в этом случае m +2 и
Определим характеристики одноканальной СМО с ожиданием и ограниченной длиной очереди, равной m:
Вероятность отказа в обслуживании заявки (отказ произойдет в случае, если канал занят и в очереди находятся m заявок):
(0‑4)
Относительная пропускная способность.
(0‑5)
Абсолютная пропускная способность.
; (0‑6)
Среднее число находящихся в очереди заявок.
В случае, когда ρ отлично от 1, можно воспользоваться формулой
При ρ = 1 можно прибегнуть к прямому подсчету
(0‑8)
Среднее число находящихся в системе заявок.
Поскольку среднее число находящихся в системе заявок
(0‑9)
где - среднее число заявок, находящихся под обслуживанием, то зная остается найти . Т.к. канал один, то число обслуживаемых заявок может равняться либо 0, либо 1 с вероятностями P0 и P1=1- P0 соответственно, откуда
(0‑10)
и среднее число находящихся в системе заявок равно
(0‑11)
Среднее время ожидания заявки в очереди.
т.е., среднее время ожидания заявки в очереди равно среднему числу заявок в очереди, деленному на интенсивность потока заявок.
Среднее время пребывания заявки в системе.
Время пребывания заявки в системе складывается из времени ожидания заявки в очереди и времени обслуживания . Если загрузка системы составляет 100%, то =1/μ, в противном случае =q/ μ. Отсюда
(0‑13)
Содержание работы.
Подготовка инструментария эксперимента.
Выполняется аналогично в соответствии с общими правилами.
Расчет на аналитической модели.
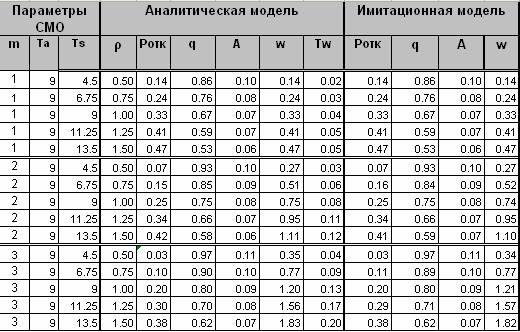
1. В приложение Microsoft Excel подготовьте таблицу следующего вида.

2. В столбцах для параметров СМО таблицы запишите исходные данные, которые определяются по правилу:
m=1,2,3
(максимальная длина очереди).
Для каждого значения m необходимо найти теоретические и экспериментальные значения показателей СМО для таких пар значений:
= <порядковый номер в списке группы>
3. В столбцы с показателями аналитической модели впишите соответствующие формулы.
Эксперимент на имитационной модели.
1. Установите режим запусков с экспоненциально распределенным временем обслуживания, задав значение соответствующего параметра равным 1.
2. Для каждой комбинации m, и осуществите запуск модели.
3. Результаты запусков внесите в таблицу.
4. Внесите в соответствующие столбцы таблицы формулы для расчета среднего значения показателя Pотк, q и А.
Анализ результатов.
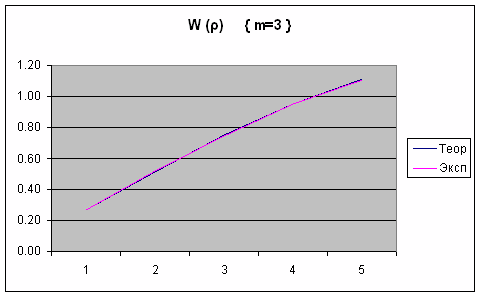
1. Проанализируйте результаты, полученные теоретическим и экспериментальным способами, сравнив результаты между собой.
2. Для m=3 постройте на одной диаграмме графики зависимости Pотк от на теоретически и экспериментально полученных данных.
Оптимизация параметров СМО.
Решите задачу оптимизации размера числа мест в очереди m для прибора со средним временем обслуживания = с точки зрения получения максимальной прибыли. В качестве условий задачи возьмите:
- доход от обслуживания одной заявки равным 80 у.е./час,
- стоимость содержания одного прибора равным 1у.е./час.
1. Для расчетов целесообразно создать таблицу:

Первый столбец заполняется значениями чисел натурального ряда (1,2,3…).
Все клетки второго и третьего столбцов заполняются значениями и .
В клетки столбцов с четвертого по девятый переносятся формулы для столбцов таблицы раздела 0.
В столбцы с исходными данными разделов Доход, Расход, Прибыль внесите значения (см. выше).
В столбцах с вычисляемыми значениями разделов Доход, Расход, Прибыль запишите расчетные формулы:
- число заявок в единицу времени
Nr=A
- суммарный доход в единицу времени
IS= Ir*Nr
- суммарный расход в единицу времени
ES=Es + Eq*(n-1)
- прибыль в единицу времени
P= IS- ES
где
- Ir - доход от одной заявки,
- Es - расход на эксплуатацию одного прибора,
- Eq - расход на эксплуатацию одного места в очереди.
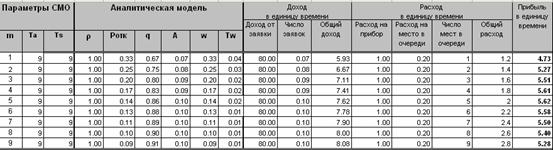
mопт=5
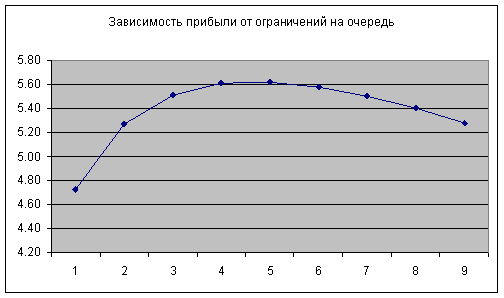
2. Постройте график зависимости C(m).
Отчет по работе:
Отчет по работе должен включать:
- исходные данные,
- результаты расчетов и экспериментов с программной моделью,
- графики для Pотк,
- таблицу с данными для нахождения наилучшего m и значение mопт,
- график зависимости прибыли в единицу времени от m.
Контрольные вопросы:
1)Дайте краткое описание одноканальной модели СМО с ограниченной очередью.
2)Какими показателями характеризуется функционирование одноканальной СМО с отказами?
3)Как рассчитывается вероятность p0?
4)Как рассчитываются вероятности pi?
5)Как найти вероятность отказа обслуживания заявки?
6)Как найти относительную пропускную способность?
7)Чему равна абсолютная пропускная способность?
8)Как подсчитывается среднее число заявок в системе?
9)Приведите примеры СМО с ограниченной очередью.
Задачи.
1)Порт имеет один грузовой причал для разгрузки судов. Интенсивность потока составляет 0,5 заходов в сутки. Среднее время разгрузки одного судна 2 суток. Если в очереди на разгрузку стоят 3 судна, то приходящее судно направляется для разгрузки на другой причал. Найти показатели эффективности работы причала.
2)В справочную железнодорожного вокзала поступают телефонные запросы с интенсивностью 80 заявок в час. Оператор справочной отвечает на поступивший звонок в среднем 0,7 мин. Если оператор занят, клиенту выдается сообщение "Ждите ответа", запрос становится в очередь, длина которой не превышает 4 запросов. Дайте оценку работы справочной и вариант ее реорганизации