5. Многоканальная СМО с отказами

(к оглавлению)

 

Цель работы:

-   Овладение аналитическими методами и методами имитационного моделирования исследования многоканальных систем массового обслуживания.

-   Решение задач оптимизации параметров систем массового обслуживания

 

Теоретические сведения

 

В отличие от модели одноканальной СМО с отказами (потерями) в модели многоканальной СМО используется n>1 обслуживающих приборов с одинаковой интенсивностью обслуживания µ. Входной поток заявок и поток обслуживания заявок являются пуассоновскими. Как и в случае одноканальной СМО на ее вход поступает пуассоновский поток заявок с интенсивностью λ. Заявка, заставшая хотя бы один канал свободным, поступает на обслуживание, которое продолжается в течение случайного времени Ts, распределенного по показательному закону с параметром µ. Заявка, заставшая все каналы занятыми, получает отказ и покидает систему необслуженной.

Предельные вероятности состояний, под которыми подразумевается число занятых обслуживанием каналов, имеют вид:

 (0‑1)

где

 .

 

(последнее равенство в выражении для P0 справедливо только при достаточно большом n).

Эти соотношения называют формулами Эрланга. Они выражают предельные состояния в зависимости от значений параметров λ и μ.

Вероятностные характеристики многоканальной СМО с отказами в стационарном режиме можно получить, используя следующие выражения.

 

Вероятность отказа.

Заявка получает отказ, если все каналы заняты. Вероятность этого равна:

 

 (0‑2)

 

Относительная пропускная способность.

Вероятность того, что заявка будет принята к обслуживанию (относительная пропускная способность q) есть дополнение  до 1:

 (0‑3)

 

Абсолютная пропускная способность.

 

 (0‑4)

 

Среднее число заявок в системе (среднее число занятых каналов).

Среднее число заявок в системе можно подсчитать через вероятности P0, P1, …, Pk,… Pn, по формуле

 

 (0‑5)

 

как математическое ожидание дискретной случайной величины.

 

Однако, проще выразить среднее число занятых каналов через абсолютную пропускную способность А, которая уже известна. Так как А есть среднее число заявок, обслуживаемых в единицу времени, а один занятый канал обслуживает в среднем μ заявок в единицу времени, то среднее число занятых каналов получается делением А на μ

 

 (0‑6)

или переходя к обозначению :

 (0‑7)

 

Содержание работы.

Подготовка инструментария эксперимента.

Выполняется в соответствии с общими правилами.

 

Расчет на аналитической модели.

1. В приложение Microsoft Excel подготовьте таблицу следующего вида.

 

 

2. В столбцах для параметров СМО таблицы запишите свои исходные данные, которые определяются по правилу:

 

n=1,2,3

 

По каждому n необходимо найти теоретические и экспериментальные значения показателей СМО для пяти пар значений:

 = <порядковый номер в списке группы>

 

3. В столбцы с показателями аналитической модели впишите соответствующие формулы.

 

Эксперимент на имитационной модели.

1. Установите режим запусков с экспоненциально распределенным временем обслуживания, задав значение соответствующего параметра равным 1.

2. Для каждой комбинации n,  и  осуществите запуск модели.

3. Результат запуска внесите в таблицу.

4. Внесите в соответствующие столбцы таблицы формулы для расчета среднего значения показателя Pотк, q и А.

 

 

Анализ результатов.

1. Проанализируйте результаты, полученные теоретическим и экспериментальным способами, сравнив результаты между собой.

2. Для каждого n постройте на одной диаграмме графики зависимости Pотк от  на теоретически и экспериментально полученных данных.

 

 

Оптимизация параметров СМО.

Решите задачу нахождения количество приборов n со средним временем обслуживания  =  оптимальное с точки зрения получения максимальной прибыли. В качестве условий задачи возьмите:

-   доход от обслуживания одной заявки равным 80 у.е./час,

-   стоимость содержания одного прибора равным 1у.е./час.

 

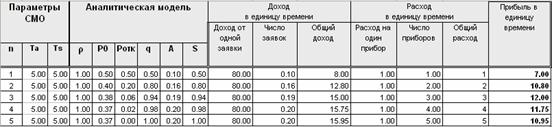
1. Для расчетов целесообразно создать таблицу:

 

 

Первый столбец заполняется значениями чисел натурального ряда (1,2,3…).

Все клетки второго и третьего столбцов заполняются значениями .

В клетки столбцов с третьего по восьмой переносятся формулы для столбцов таблицы раздела 0.

В столбцы с исходными данными разделов Доход, Расход, Прибыль внесите значения.

В столбцах с вычисляемыми значениями разделов Доход, Расход, Прибыль запишите расчетные формулы:

- число заявок в единицу времени

Nr=A

- суммарный доход в единицу времени

IS= Ir*Nr

- суммарный расход в единицу времени

ES=Ed*n

- прибыль в единицу времени

P= IS- ES

где

-    Ir - доход от одной заявки,

-    Ed - расход на один прибор.

 

2. Среди нескольких значений n определите такое nопт, при котором достигается максимум целевой функции:

 

 

nопт=3

 

3. Постройте график зависимости прибыли в единицу времени от числа обслуживающих приборов:

 

 

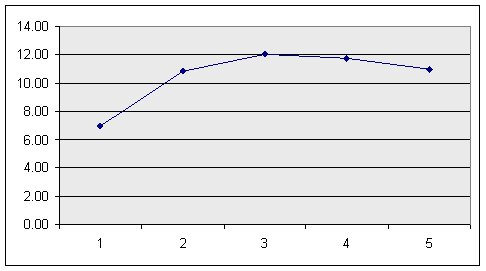
Отчет по работе:

Отчет по работе должен включать:

-   исходные данные,

-   результаты расчетов и экспериментов с программной моделью,

-   графики для Pотк,

-   таблицу с данными для нахождения наилучшего n и значение nопт,

-   график зависимости прибыли в единицу времени от n.

 

Контрольные вопросы:

1)Дайте краткое описание многоканальной модели СМО с отказами

2)Какими показателями характеризуется функционирование многоканальной СМО с отказами?

3)Как рассчитывается вероятность p0?

4)Как рассчитываются вероятности pi?

5)Как найти вероятность отказа обслуживания заявки?

6)Как найти относительную пропускную способность?

7)Чему равна абсолютная пропускная способность?

8)Как подсчитывается среднее число заявок в системе?

9)Приведите примеры СМО с отказами.

 

Задачи.

1)В мастерской по ремонту обуви работают четыре мастера, каждый из которых выполняет заказ в среднем за 20 мин. Клиенты заходят в мастерскую в среднем каждые 25 мин и, если мастера заняты, то уходят. Определить характеристики работы обувной мастерской и отношение “заработанные деньги/не заработанные деньги”, если средняя стоимость ремонта составляет 70 руб.

2)Дайте оценку работы телефонной компании, если она располагает четырьмя каналами связи, за один час поступает в среднем 120 телефонных звонков, а среднее время ответа на звонок составляет 1,2 мин.

3)В типографию с тремя множительными аппаратами поступают заказы от соседних предприятий на размножение рабочей документации. Если все аппараты заняты, то вновь поступающий заказ не принимается. Среднее время работы с одним заказом составляет 2 часа. Интенсивность потока - 0,5 заявки в час. Необходимо найти предельные вероятности состояний и показатели эффективности работы типографии.

4)Дайте оценку работы предприятия, если у нее имеется 6 каналов связи, за один час поступает в среднем 200 телефонных звонков, среднее время ответа на звонок - 0,8 мин.

5)Около магазина имеется парковка для 7 машин. Автомашины подъезжают к магазину с интенсивностью 40 машин в час. Продолжительность нахождения на автостоянке составляет в среднем 20 мин. Стоянка на проезжей части улицы не допускается. Определить характеристики работы парковки.