4. Одноканальная СМО с отказами
(к оглавлению)
Цель работы:
Овладение аналитическими методами и методами имитационного моделирования исследования одноканальных систем массового обслуживания.
Теоретические сведения
Модель одноканальной системы массового обслуживания (СМО) с отказами (потерями) является простейшей из всех моделей, используемых для решения задач теории массового обслуживания.
Система массового обслуживания в этом случае состоит только из одного канала (n = 1) и на нее поступает пуассоновский поток заявок с интенсивностью λ, которую будем считать не зависящей от времени.
Заявка, заставшая канал занятым, получает отказ и покидает систему необслуженной.
Заявка, заставшая канал свободным, поступает на обслуживание, которое продолжается в течение случайного времени Тs, распределенного по показательному закону с параметром µ:
(0‑1)
Поток обслуживания представляет собой, таким образом, простейший (пуассоновский) поток с интенсивностью µ. Чтобы представить себе этот поток, можно вообразить один непрерывно занятый канал, который будет формировать поток обслуженных заявок интенсивности µ.
СМО с отказами характеризуются следующими величинами.
Относительная пропускная способность – отношение среднего числа обслуженных заявок за единицу времени к среднему числу всех поступивших заявок за тоже время, т.е. средняя доля обслуженных заявок среди всех поступивших.
Абсолютная пропускная способность – среднее число заявок, которое может обслужить СМО в единицу времени.
Вероятность отказа – средняя доля не обслуженных заявок среди всех поступивших.
Нахождение предельных вероятностей состояний системы p0 (вероятность того, что в системе находится 0 заявок) и p1 (вероятность того, что в системе находится 1 заявка) несложно отыскивается на основании решений уравнений Колмогорова для стационарного режима:
(0‑2)
(0‑3)
Для одноканальной СМО с отказами вероятность р0 есть не что иное, как относительная пропускная способность q. Действительно, p0 есть вероятность того, что в момент t канал свободен, или вероятность того, что заявка, пришедшая в момент t, будет обслужена. Следовательно, для данного момента времени t среднее отношение числа обслуженных заявок к числу поступивших также равно р0 (q= р0).
В установившемся режиме обслуживания предельное значение относительной пропускной способности будет равно
(0‑4)
Зная относительную пропускную способность q, легко найти абсолютную пропускную способность А. Они связаны очевидным соотношением:
(0‑5)
В установившемся режиме обслуживания предельное значение относительной пропускной способности будет равно
(0‑6)
Зная относительную пропускную способность системы q (вероятность того, что пришедшая в момент t заявка будет обслужена), легко найти вероятность отказа, или долю необслуженных заявок среди пришедших:
(0‑7)
В установившемся режиме
(0‑8)
Содержание работы.
Подготовка инструментария эксперимента.
Выполняется в соответствии с общими правилами.
Расчет на аналитической модели.
1. В приложении Microsoft Excel подготовьте таблицу следующего вида.
2. В двух первых столбцах таблицы запишите свои исходные данные (средний интервал между заявками входного потока и среднее время обслуживания в канале соответственно), которые определяются по правилу
= <порядковый номер в списке группы>
3. В столбцы с третьего по пятый впишите формулы для расчета показателей Pотк, q и A.
Эксперимент на имитационной модели.
1. Задайте режим запусков с экспоненциально распределенным временем обслуживания, задав значение соответствующего параметра равным 1.
2. Для каждой комбинации и осуществите запуск модели.
3. Результаты запусков внесите в таблицу.
4. Внесите в соответствующие столбцы таблицы формулы для расчета среднего значения показателя Pотк, q и А.
5. Повторите пп.1-3 для детерминированного закона времени обслуживания заявок, задав значение соответствующего параметра равным 2.
Анализ результатов.
1)Проанализируйте результаты, полученные теоретическим и экспериментальным способами, сравнив результаты между собой.
2)Постройте на одной диаграмме графики зависимости Pотк от на теоретически и экспериментально полученных данных для случая экспоненциально распределенного времени обслуживания.
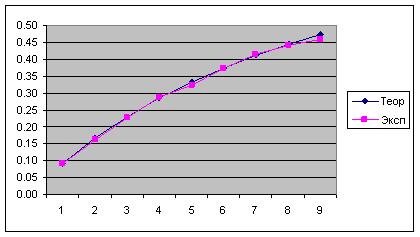
3)Выполните предыдущий пункт на экспериментально полученных данных для случаев экспоненциально распределенного и детерминированного времени обслуживания.
Отчет по работе:
Отчет по работе должен включать:
- Исходные данные,
- Таблицу с расчетными и экспериментальными результатами,
- Графический материал согласно описаниям предыдущих пунктов.
Контрольные вопросы:
1)Дайте краткое описание модели СМО с отказами.
2)Какими показателями характеризуется функционирование СМО с отказами?
3)Как рассчитывается вероятность p0?
4)Как рассчитывается вероятность p1?
5)Что такое относительная пропускная способность?
6)Что такое абсолютная пропускная способность?
7)Чему равна вероятность отказа обслуживания заявки?
8)Приведите примеры СМО с отказами.
Задачи.
1)На телефонную линию поступает простейший поток вызовов с интенсивностью l = 0,9 вызовов в минуту. Производительность телефонной линии m = 0,7 вызовов в минуту. Определить относительную и абсолютную пропускную способности, вероятность отказа и среднее время простоя канала.
2)Справочное бюро имеет одну телефонную линию, на которую приходится в среднем 0,4 вызова в минуту. Среднее время разговора 1,3 мин. Считая потоки простейшими, найти абсолютную и относительную пропускные способности справочного бюро и вероятность отказа абоненту.
3)Сборочный участок производит в один час 90 блоков, т.е. интенсивность потока l =1.5 блоков в минуту. На этом участке работает контролер, который выборочно проверяет изготовленные блоки аппаратуры, средняя продолжительность контрольных операций равна 1,25 минут. Если в момент прибытия очередного блока контролер занят, то этот блок сразу же передается на дальнейшие операции без промежуточного контроля. Производство непрерывное и продолжается до обнаружения дефекта в одном из блоков, в этом случае технологический процесс останавливается, и выясняются причины неисправности. Необходимо определить, какая часть продукции в таких условиях подвергается контролю, и какая часть продукции пропускается на дальнейшие операции без контроля (т.е. какая часть получает отказ от прохождения контрольных операций).
4)В мастерской по ремонту обуви в понедельник работает только один мастер, который выполняет заказ в среднем за 25 мин. Клиенты заходят в мастерскую в среднем каждые 35 мин и в случае занятости мастера уходят. Определить характеристики работы обувной мастерской и отношение заработанные деньги/не заработанные деньги, если средняя стоимость ремонта составляет 80 руб.
5)В результате наблюдений установлено, что интенсивность телефонных звонков диспетчеру жилищно-эксплуатационной конторы, имеющих характер простейших пуассоновских потоков, составляет 1,1 вызовов в минуту, средняя продолжительность разговора (обслуживание клиента) составляет 2,3 мин. Определить характеристики работы диспетчера конторы также количество обслуженных и не обслуженных клиентов за 1 час работы. Сравнить фактическую пропускную способность с номинальной (когда каждый клиент обслуживается 2,5 мин).