3. Марковские процессы

(к оглавлению)

 

Цель работы:

-   Изучение аналитических методов описания марковских случайных процессов.

-   Исследование процессов гибели и размножения на аналитической и имитационной модели.

 

Теоретические сведения

 

Основные понятия и определения.

Пусть имеется некоторая система S, состояние которой меняется с течением времени (под системой S может пониматься техническое устройство, производственный процесс, вычислительная машина, информационная сеть и т. д.). Если состояние системы S меняется во времени случайным, заранее непредсказуемым образом, говорят, что в системе протекает случайный процесс.

Случайный процесс, протекающий в системе S, называется марковским (или “процессом без последействия”), если он обладает следующим свойством: для каждого момента времени t0 вероятность любого состояния системы в будущем (при t>t0) зависит только от ее состояния в настоящем (при t= t0) и не зависит от того, когда и каким образом система пришла в это состояние (т. е. как развивался процесс в прошлом).

Марковский случайный процесс (цепь Маркова) можно определить также как последовательность испытаний, в каждом из которых появляется только одно из k несовместных событий Ai из полной группы. При этом условная вероятность pij(s) того, что в s –ом испытании наступит событие Aj при условии, что в (s – 1) – ом испытании наступило событие Ai, не зависит от результатов предшествующих испытаний. Независимые испытания являются частным случаем цепи Маркова. События называются состояниями системы, а испытания – изменениями состояний системы.

Марковские случайные процессы делятся на классы. Основными классифицирующими признаками являются:

-   множество состояний, в которых может находиться система, и

-   моменты времени, в которых происходит изменение состояния системы.

 

Случайный процесс называется процессом с дискретными состояниями, если возможные состояния системы S₁, S₂, S₃, ... можно перечислить (перенумеровать) одно за другим, а сам процесс состоит в том, что время от времени система S скачком (мгновенно) переходит из одного состояния в другое.

Кроме процессов с дискретными состояниями существуют случайные процессы с непрерывными состояниями: для этих процессов характерен постепенный, плавный переход из состояния в состояние. Например, процесс изменения напряжения в осветительной сети представляет собой случайный процесс с непрерывными состояниями.

Если переходы системы из состояния в состояние возможны только в определенные моменты времени t₁, t₂, t₃,…, то марковский процесс относится к процессам с дискретным временем. В противном случае имеет место процесс с непрерывным временем.

Анализ случайных процессов с дискретными состояниями обычно проводится с помощью графа состояний и переходов (ГСП).

Пусть имеется система S с n дискретными состояниями:

 

S1, S2, S3, …Sn

 

Каждое состояние изображается прямоугольником, а возможные переходы (“перескоки”) из состояния в состояние — стрелками, соединяющими эти прямоугольники. Удобно также пользоваться размеченным графом, который графически изображает не только возможные состояния системы и возможные переходы из состояния в состояние, но также и значения вероятностей перехода.

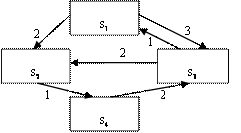
Примеры ГСП показаны на

Рисунок 0‑1.

 

 

Рисунок 0‑1. Примеры графа состояний и переходов

 

Графу системы, содержащему n вершин, можно поставить в соответствие матрицу n×n, элементами которой являются вероятности переходов pij между вершинами графа, называемую матрицей вероятностей переходов. Элементы матрицы  удовлетворяют условиям:

 

 (0‑1)

 (0‑2)

 

Условие (0‑1) - обычное свойство вероятностей, а условие (0‑2) означает, что система S обязательно либо переходит из какого-то состояния Si в другое состояние, либо остается в состоянии Si. Элементы pij матрицы P обозначают вероятности переходов в системе за один шаг.

Обычно на графе вероятности перехода системы из одного состояния в то же самое не отмечаются. При рассмотрении конкретных систем удобно сначала построить граф состояний, затем определить вероятность переходов системы из одного состояния в то же самое (исходя из требования равенства единице суммы элементов строк матрицы), а потом составить матрицу переходов системы.

 

Марковский процесс с дискретными состояниями и дискретным временем.

Пусть система S может находиться в состояниях:

 

S1, S2, S3, … Sn

 

и изменения состояния системы возможны только в моменты:

 

t1, t2, t3, …tn

 

Будем называть эти моменты шагами, или этапами процесса и рассматривать протекающий в системе S случайный процесс как функцию целочисленного аргумента m = 1, 2, ... k, ..., обозначающего номер шага.

Указанный случайный процесс состоит в том, что в последовательные моменты времени t₁, t₂, ..., t_k, ... система S оказывается в тех или иных состояниях. Процесс, происходящий в системе, можно представить как последовательность (цепочку) событий, например:

 

называемую марковской цепью, где для каждого шага вероятность перехода из любого состояния S_i в любое S_j не зависит от того, когда и как система пришла в состояние S_i .

Марковскую цепь можно описать с помощью вероятностей состояний, в которых находится система на каком-то шаге. Пусть в любой момент времени (после любого шага) система может пребывать в одном из состояний:

 

S₁, S₂, S₃, ….S_n

 

т. е., в результате шага k осуществится одно из полной группы несовместных событий:

 

 

Обозначив вероятности этих событий для k -го шага через

 

 

легко видеть, что для каждого шага k

 

 

поскольку , представляют собой вероятности появления полной группы событий.

Вероятности  называются вероятностями состояния.

Для любого шага (момента времени t₁,t₂,...t_k,... или номера 1,2,...,k,...) существуют некоторые вероятности перехода системы из любого состояния в любое другое (некоторые из них равны нулю, если непосредственный переход за один шаг невозможен), а также вероятность задержки системы в данном состоянии. Эти вероятности называются переходными вероятностями марковской цепи.

Если значения переходных вероятностей не зависят от номера шага, то марковская цепь называется однородной, или стационарной. В противном случае марковская цепь является неоднородной, или нестационарной.

Для графа

Рисунок 0‑1 значения переходных вероятностей  будут равны:

 

 

Если из состояния S_i не исходит ни одной стрелки (переход из него ни в какое другое состояние невозможен), соответствующая вероятность задержки Р_ii равна единице.

Имея в распоряжении размеченный ГСП (или, что равносильно, матрицу переходных вероятностей) и зная начальное состояние системы, можно найти вероятности состояний р₁(k), р₂(k), ... р_n(k) после любого (k-го) шага. Они находятся с помощью следующих рекуррентных соотношений:

 

 (0‑3)

 

или в матричной форме

 

 (0‑4)

 

Марковский процесс с дискретными состояниями и непрерывным временем.

На практике встречаются ситуации, когда переходы системы из состояния в состояние происходят не в фиксированные, а в случайные моменты времени, которые заранее указать невозможно — переход может осуществиться в любой момент. Например, выход из строя (отказ) любого элемента аппаратуры может произойти в любой момент времени; окончание ремонта (восстановление) этого элемента также может произойти в заранее неизвестный момент и т. д.

Для описания таких процессов может быть применена схема марковского случайного процесса с дискретными состояниями и непрерывным временем. Такого типа процессы известны как непрерывные цепи Маркова. Непрерывной цепью Маркова (марковским процессом) называют процесс, для которого при 0≤ t1≤ t2≤ …tn+1 выполняется:

 

 

Здесь так же, как и в случае процесса с дискретным временем, рассматривается ряд дискретных состояний: S₁, S₂, S₃, ..., S_n, однако переход системы S из состояния в состояние может происходить в произвольный момент времени.

Обозначим p_i(t) — вероятность того, что в момент t система S будет находиться в состоянии S_i (i= 1, ..., n). Очевидно, для любого момента t сумма вероятностей состояний равна единице:

 

 (0‑5)

 

так как события, состоящие в том, что в момент t система находится в состояниях S₁, S₂,, ..., S_n , несовместны.

Необходимо определить для любого t вероятности состояний:

 

 (0‑6)

 

Для того чтобы найти эти вероятности, необходимо знать характеристики процесса, аналогичные переходным вероятностям для Марковской цепи. В случае процесса с непрерывным временем вместо переходных вероятностей P_ij рассматриваются плотности вероятностей (или интенсивности) перехода λ_ij (поскольку вероятность перехода системы из состояния в состояние точно в момент t будет равна нулю, так же, как вероятность любого отдельного значения непрерывной случайной величины).

Пусть система S в момент t находится в состоянии S_r Рассмотрим элементарный промежуток времени Δt, примыкающий к моменту t. Назовем плотностью вероятности перехода λ_ij из состояния i в состояние j предел (или инфинитезимальными коэффициентами) отношение вероятности перехода системы за время Δt из состояния S_i в состояние S_j к длине промежутка Δt:

 (0‑7)

 

где Pij(Δt) — вероятность того, что система, находившаяся в момент t в состоянии S_i, за время Δt перейдет из него в состояние S_j (плотность вероятностей перехода определяется только для j≠i). Из (0‑7) следует, что при малом Δt вероятность перехода (с точностью до бесконечно малых высших порядков) равна:

 

Pij(Δt)=λij Δt

 

Если все плотности вероятностей перехода λ_ij не зависят от t (от того, в какой момент начинается элементарный участок Δt  ), марковский процесс называется однородным, а если эти плотности зависят от времени, то он является неоднородным.

Анализ случайных процессов с непрерывным временем так же как марковских процессов с дискретным временем удобно производить с помощью графа состояний и переходов (Рисунок 0‑2), на основании которого можно определить вероятности состояний р_i(t) (0‑6) как функции времени.

 

 

 

Рисунок 0‑2 Пример размеченного графа непрерывной цепи Маркова

 

Распределение вероятностей состояний системы, которое можно характеризовать вектором  называется стационарным, если оно не зависит от времени, т.е. все компоненты вектора  являются константами.

Выходными характеристиками марковского процесса с дискретным множеством состояний и непрерывным временем являются:

-   нестационарное распределение вероятностей ;

-   стационарное распределение вероятностей ;

-   среднее время пребывания в фиксированном множестве состояний;

-   интенсивности перехода из одного множества состояний в другое.

 

Весьма важным является вопрос о поведении функций р₁(t), р₂(t), ..., р_n(t) при , а именно, будут ли они стремиться к каким-то пределам. Если эти пределы существуют, они называются предельными (финальными) вероятностями состояний.

 

 (0‑8)

 

Очевидно, предельные вероятности состояний в сумме должны давать единицу:

 

 (0‑9)

 

Доказано, что если число состояний системы S конечно и из каждого состояния можно перейти (за то или иное число шагов) в любое другое, то предельные вероятности состояний существуют и не зависят от начального состояния системы.

Таким образом, при  в системе S устанавливается некоторый предельный стационарный режим: хотя система случайным образом и меняет свои состояния, но вероятность каждого из них не зависит от времени и каждое из состояний осуществляется с некоторой постоянной вероятностью, которая представляет собой среднее относительное время пребывания системы в данном состоянии. Это свойство позволяет обходиться при нахождении параметров системы на основе моделирования одной достаточно длинной реализацией.

Для вероятностей p1(t), p2(t),…, pn(t) можно составить систему линейных дифференциальных уравнений, называемых уравнениями Колмогорова, которые в случае нахождения предельных вероятностей превращаются в систему линейных алгебраических уравнений (уравнений глобального баланса) для каждого состояния. Совместно с нормировочным условием (0‑9) эти уравнения дают возможность вычислить все предельные вероятности (0‑8).

Общее правило составления уравнений Колмогорова для предельных вероятностей pi(t) можно сформулировать следующим образом:

-   в левой части уравнения стоит сумма произведений вероятностей всех состояний, из которых идут стрелки в i‑ое состояние, на интенсивности соответствующих потоков минус сумма интенсивностей всех потоков, выводящих систему из данного (j-го) состояния, умноженная на вероятность данного (j-го) состояния;

-   в правой части уравнения стоит 0.

 

Пример:

Уравнения для ГСП на Рисунок 0‑2 будут иметь вид:

 

 

Для получения системы независимых уравнений одно из уравнений следует заменить на условие нормировки(0‑9):

 

р₁+ р₂ + р₃ + р₄ = 1

 

Процессы гибели и размножения.

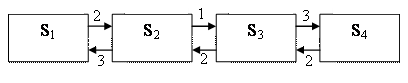
Примером составления уравнений для нахождения предельных вероятностей могут служить процессы гибели и размножения, ГСП для которых имеет вид:

 

 

Рисунок 0‑3 ГСП для процесса размножения и гибели

 

Запишем алгебраические уравнения для вероятностей состояний. В стационарных условиях для каждого состояния интенсивность потока, втекающего в данное состояние, должна равняться интенсивность потока, вытекающего из данного состояния.

Для первого состояния S₁ имеем:

 (0‑10)

 

Для второго состояния S₂ суммы членов, соответствующих входящим и выходящим стрелкам, равны:

 

 

Но в силу (0‑10) можно сократить справа и слева равные друг другу члены и тогда получим:

 

 

и далее, совершенно аналогично,

 

 

и т. д.

Очевидно, для этого случая члены, соответствующие стоящим друг над другом стрелкам, равны между собой:

 

 (0‑11)

 

где k принимает все значения от 2 до n.

 

Итак, предельные вероятности состояний

 

р = (р₁, р₂. ..., р_n)

 

в любой схеме размножения и гибели удовлетворяют уравнениям:

 

 (0‑12)

 

и нормировочному условию (0‑9):

 

 

Решение этой системы имеет вид

 

 

 (0‑13)

 

Пример.

Техническое устройство состоит из трех одинаковых узлов, каждый из которых может выходить из строя (отказывать). Отказавший узел немедленно начинает восстанавливаться. Требуется найти вероятности числа отказавших узлов.

Решение.

Состояния системы:

S₁ — все три узла исправны:

S₂ — один узел отказал (восстанавливается), два исправны;

S ₃ — два узла восстанавливаются, один исправен;

S ₄ — все три узла восстанавливаются.

ГСП имеет вид:

 

 

Из графа видно, что процесс, протекающий в системе, представляет собой процесс размножения и гибели.

По формулам (0‑13) получаем:

 

 

Задание.

В работе требуется провести расчет системы, состоящей из n узлов. Каждый из узлов может находиться в исправном или неисправном состоянии. После выхода узла из строя он начинает немедленно восстанавливаться. Протекающий в системе процесс можно считать марковским. Все узлы однотипны. Это означает, что все они имеют одни и те же значения интенсивностей выхода из строя l и восстановления m.

 

Подготовка инструментария эксперимента.

Выполняется в соответствии с общими правилами.

 

Расчет на аналитической модели.

1. Откройте приложение Microsoft Excel и создайте книгу для промежуточных и итоговых данных по работе.

2. Внесите в таблицу исходные данные для своего варианта, например:

 

 

Число устройств и значения интенсивностей l и m приведены в разделе 0.

3. Постройте размеченный ГСП процесса.

Очевидно, что размеченный ГСП системы представляет собой размеченный ГСП процесса гибели и размножения.

В случае, когда используются однотипные узлы, удобнее пронумеровать состояния системы номерами, соответствующими числу неисправных узлов, т.е., 0,1,2,…n, где n - число узлов. Тогда значения  и  будут определяться выражениями:

 

 

и

 

 

где  есть значения интенсивностей выхода из строя и восстановления узла соответственно.

Используя любой известный графический редактор нарисуйте граф в виде рисунка на Excel – листе (в примере число узлов равно 6):

 

 

В случае затруднений с электронным изображением допускается построение ГСП в рукописном виде.

4. Проведите расчет вероятностей нахождения системы в каждом из своих состояний с помощью аналитических выражений аппарата марковских процессов.

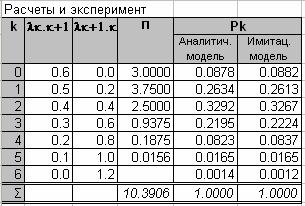
Для проведения расчетов создайте таблицу со структурой

 

 

в которой столбцы 1,2,…6 используются следующим образом:

1- номер состояния,

2- интенсивность перехода из данного состояния в состояние с номером на 1 большим,

3- интенсивность перехода из состояния с номером на 1 большим в данное состояние,

4- значения каждого слагаемого, стоящего в выражении для вычисления Р0 (без 1),

5- аналитически вычисленные значения Рк,

6- найденные с помощью имитационной модели значения Рк.

 

Таблица должна содержать по одной строке для каждого состояния и одну строку для сумм по столбцам 4,5,6.

Точность для первого столбца таблицы установите равной одному десятичному знаку, для второго и третьего – двум десятичным знакам, для четвертого, пятого и шестого – четырем десятичным знакам.

Эксперимент на имитационной модели.

1. Установите режим запусков с экспоненциально распределенным временем обслуживания, задав значение соответствующего параметра равным 1.

2. Найдите значения вероятностей нахождения системы в каждом из своих состояний с помощью имитационной модели. Результаты прогонов занесите в столбец 6.

 

 

Анализ результатов.

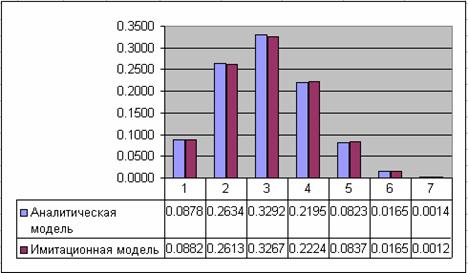
1. Проанализируйте результаты, полученные теоретическим и экспериментальным способами. Сравните результаты между собой.

2. Постройте гистограммы для вероятностей состояний системы.

 

 

Отчет по работе:

Отчет по работе должен включать:

-   Исходные данные работы,

-   Размеченный ГСП процесса,

-   Таблицу с расчетными и экспериментальными данными,

-   Гистограмму предельных вероятностей.

Контрольные вопросы:

1)Дайте определение марковского процесса.

2)Как классифицируются марковские процессы?

3)Что такое граф состояний и переходов (ГСП) Марковской цепи? Какие бывают ГСП?

4)Что понимается под матрицей переходных вероятностей?

5)Как можно найти вероятность нахождения процесса в определенном состоянии после определенного числа шагов?

6)Что такое нестационарная марковская цепь?

7)Дайте определение марковского процесса с непрерывным временем и дискретными состояниями.

8)Что такое предельные вероятности марковского процесса? Каков физический смысл предельных вероятностей?

9)Как найти предельные вероятности системы, имеющей стационарный режим?

10)   Что называется процессами гибели и размножения? Поясните на ГСП.

11)   Запишите выражения для предельных вероятностей процесса гибели и размножения.

 

Задачи.

1)Постройте матрицу переходов и определите вероятности состояний через три шага процесса для системы, описываемой следующим ГСП:

 

 

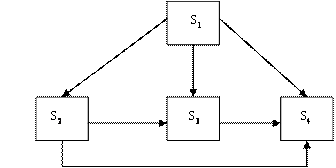
Вероятности переходов имеют следующие значения Р12=0,3; Р13=0,4; Р23=0,1; Р24=0,2; Р25=0,3; Р45=0,3; Р53=0,2.

2)Производятся три выстрела по цели, которая может находиться в четырех состояниях:

-   S1 —невредима;

-   S2 —незначительно повреждена;

-   S3 —получила существенные повреждения;

-   S4 —полностью поражена.

 

Вероятности перехода для трех последовательных выстрелов различны и задаются тремя матрицами:

 

 

В начальный момент система находится в состоянии S1.

Найдите вектор вероятностей Р(3).

 

3)Устройство S состоит из двух узлов A и B, каждый из которых в процессе работы может отказывать. Возможны следующие состояния системы:

-   S1 – оба узла работают;

-   S2 – узел A отказал, B работает;

-   S3 – узел B отказал, A работает;

-   S4 – оба узла отказали.

 

Постройте ГСП системы (для двух случаев: возможность и невозможность одновременного выхода из строя обоих узлов).

4)Система S, как и в задаче 3), представляет собой устройство, состоящее из двух узлов A и B, каждый из которых может в какой-то момент времени отказать. Отказавший узел немедленно начинает восстанавливаться. Возможны такие состояния системы:

-   S1 - оба узла работают;

-   S2 - узел A восстанавливается, узел B - работает;

-   S3 - узел A работает, узел B восстанавливается;

-   S4 - оба узла восстанавливаются.

Постройте ГСП.

5)В условиях задачи 4) каждый узел перед тем, как начать восстанавливаться, подвергается осмотру с целью локализации неисправности. Состояния системы будем теперь нумеровать не одним, а двумя индексами: первый индекс будет означать состояния узла A:

1 — работает,

2 — осматривается,

3 — восстанавливается;

второй индекс будет означать те же состояния для узла B.

(Например, S23 будет означать, что узел A осматривается, а узел B — восстанавливается.)

Постройте ГСП.

6)Измените программу (имитационную модель) таким образом, чтобы она обеспечивала нахождение значений предельных вероятностей для условий задачи 5).

7)Размеченный ГСП системы S имеет вид

 

 

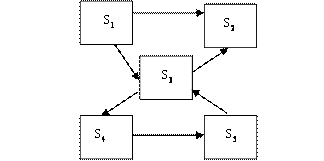
Составьте систему алгебраических уравнений для нахождения предельных вероятностей.

8)Постройте ГСП для нахождения вероятностей состояния системы, узлы которой разнотипны, т.е., характеризуются разными значениями l и m. Число узлов положите равным 3, значения l и m задайте произвольно.

Проведите расчет предельных вероятностей, после чего сверьте его с результатами прогонов на имитационной модели.

9)Осуществите запуски программной модели, задав для своего варианта детерминированный закон распределения времени безотказной работы или времени восстановления. Проанализируйте результаты.

 

Варианты исходных данных

 

Число узлов n=4.

Интенсивности отказов и восстановлений: