2. Пуассоновский поток
(к оглавлению)
Цель работы:
Изучение пуассоновского потока и методов аппроксимации теоретическим распределением данных наблюдения за входящим потоком и потоком обслуживания в системах массового обслуживания.
Теоретические сведения
Поток требований называют однородным, если:
- все требования потока обслуживаются в системе массового обслуживания одинаково;
- рассмотрение требований (событий) потока, которые по своей природе могут быть различными, ограничивается рассмотрением моментов времени их поступления.
Поток называется регулярным, если события в потоке следуют один за другим через интервалы времени одинаковой длительности.
Функция f(х) плотности распределения вероятности случайной величины Т, обозначающей интервал времени между событиями, для регулярного потока имеет вид:
где
- δ - дельта функция,
- - математическое ожидание случайной величины T.
Дисперсия интервала между событиями регулярного потока (моментами поступления требований) D[T] равна 0, а интенсивность наступления событий в потоке (среднее число требований в единицу времени) равна .
Поток называется случайным, если события в потоке следуют один за другим через интервалы времени случайной длительности.
Случайный поток может быть описан как случайный вектор, который, в свою очередь, может быть задан одним из двух способов:
1) Функцией распределения моментов наступления событий
,
где ti – значение моментов наступления Ti(i=1,n),
2) Функцией распределения интервалов между наступлением последовательных событий τ1, τ2,… τn:
где i- значения интервалов между событиями τi(i=1,n),
В последнем случае моменты наступления событий могут при необходимости быть найдены из рекуррентных соотношений:
t1=t0+
t2=t1+
………,
tn=tn-1+
……………
где t0 - момент наступления первого события потока.
Поток называется стационарным, если вероятность попадания того или иного числа событий на элементарный участок времени длиной τ зависит только от длины участка и не зависит от того, где именно на оси t расположен этот участок.
Поток событий называется потоком без последействия, если для любых непересекающихся участков времени число событий, попадающих на один из них, не зависит от того, сколько событий попало на другой.
Поток событий называется ординарным, если вероятность попадания на элементарный участок двух или более событий пренебрежимо мала по сравнению с вероятностью попадания одного события.
Поток событий, обладающий всеми тремя свойствами - стационарностью, отсутствием последействия, ординарностью - называется простейшим, или стационарным пуассоновским потоком.
Пуассоновский поток событий тесно связан с известным из теории вероятностей распределением Пуассона: число событий потока, попадающих на временной интервал некоторой величины, распределено по закону Пуассона.
Если на временной оси t, где наблюдается поток событий, выделить некоторый участок времени длины τ, начинающийся в момент t0 и заканчивающийся в момент t0 + τ, то нетрудно доказать, что вероятность попадания на этот участок ровно m событий выражается формулой:
(0‑1)
где а — среднее число событий, приходящееся на участок τ;
е — основание
натуральных логарифмов (2,71828…),
Для стационарного (простейшего) пуассоновского потока величина а равна интенсивности потока λ, умноженной на длину интервала:
где интенсивность, или плотность потока λ есть среднее число событий, приходящихся на единичный временной интервал. В зависимости от физической природы изучаемой системы интенсивность может иметь различную размерность, например, чел/мин, руб/день, кг/час, запросов/сек, документов/сутки, отправлений/сутки и т.д.
Функция распределения
,
представляющая собой по определению вероятность того, что случайная величина Т (интервал времени между событиями) не превысит значения t, имеет для пуассоновского потока следующий вид:
(0‑2)
Такой закон распределения называется показательным (или экспоненциальным) с плотностью λ. Величина λ называется также параметром показательного закона.
Математическое ожидание случайной величины равна
(0‑3)
а дисперсия составляет
(0‑4)
Среднеквадратическое отклонение случайной величины находится как квадратный корень из дисперсии:
(0‑5)
Как нетрудно видеть, математическое ожидание величины Т равно ее среднеквадратическому отклонению, что является характерной особенностью экспоненциального распределения.
Таким образом, вероятность появления m событий в заданном промежутке времени описывается пуассоновским распределением, а вероятность того, что временные интервалы между событиями потока не превзойдут некоторого наперед заданного значения, описывается экспоненциальным распределением. Это различные описания одного и того же стохастического процесса.
Пример:
По шоссе мимо наблюдателя движется в одном направлении простейший поток машин. Известно, что вероятность отсутствия машин в течение 5 минут равна 0,5. Требуется найти вероятность того, что за 10 минут мимо наблюдателя пройдет не более двух машин.
Решение. Примем за единицу времени 5 мин. В задаче требуется найти
По условию задачи
Откуда
и, подставляя в выражение для , получаем
Весьма распространенными на практике являются случаи, когда нескольких простейших потоков соединяются в один или, наоборот, из одного простейшего потока образуются несколько. При слиянии (объединении, суперпозиции) n независимых простейших потоков с интенсивностями λ1,..., λn образуется простейший поток, имеющий интенсивность λ=λ1+...+λn.
При ветвлении (разъединении) потока интенсивности λ на n направлений так, что вероятности перехода заявки в каждое из направлений равны , образуется n простейших потоков с интенсивностями λр1,..., λрn соответственно.
Любое исследование системы массового обслуживания начинается с изучения того, что необходимо обслуживать, иначе говоря, с изучения характеристик входящего потока заявок. В нетривиальных случаях требуется также обследование самой системы массового обслуживания с целью нахождения характеристик обслуживания, (потока обслуживания). Решение задач анализа и проектирования систем массового обслуживания намного упрощается в случаях, когда входящий поток и поток обслуживания являются простейшими (пуассоновскими).
Пример анализа данных наблюдения входящего потока.
Предположим, что проводилось наблюдение за потоком посетителей в отделении банка в течение 10 дней его работы. Результаты почасового наблюдения представлены в нижеследующей таблице:
|
Часы
Дни |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
2 |
4 |
2 |
3 |
4 |
3 |
5 |
2 |
|
|
2 |
3 |
2 |
3 |
2 |
7 |
2 |
3 |
3 |
|
3 |
1 |
3 |
4 |
3 |
4 |
6 |
4 |
2 |
|
4 |
4 |
4 |
4 |
5 |
9 |
3 |
4 |
4 |
|
5 |
2 |
1 |
3 |
7 |
3 |
6 |
2 |
3 |
|
6 |
3 |
2 |
3 |
4 |
5 |
5 |
3 |
2 |
|
7 |
4 |
3 |
4 |
3 |
8 |
3 |
4 |
3 |
|
8 |
1 |
2 |
2 |
4 |
3 |
4 |
2 |
4 |
|
9 |
3 |
4 |
6 |
3 |
4 |
2 |
4 |
2 |
|
10 |
2 |
2 |
3 |
5 |
6 |
4 |
2 |
5 |
Определим интенсивность входящего потока покупателей
за час работы отделения и, используя критерий Пирсона с уровнем значимости
α=0,05, подвергнем проверке гипотезу о том, что поток описывается пуассоновским
законом распределения.
Решение.
1)
Сгруппируем
данные по числу клиентов банка k,
посетивших отделение в течение часа, а результаты представим в виде Excel -
таблицы:
|
k |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
fk |
3 |
19 |
23 |
21 |
6 |
4 |
2 |
1 |
1 |
Для автоматизированного подсчета частот fk по данным, представленным в исходной таблице, следует
использовать функцию СЧЕТЕСЛИ приложения Excel.
2) Находим интенсивность потока λ:
В приложении Excel удобно вычислять интенсивность,
предварительно подсчитав в ячейках отдельной строки входящие в числитель
выражения для l произведения :
|
k |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
Σ |
|
fk |
3 |
19 |
23 |
21 |
6 |
4 |
2 |
1 |
1 |
80 |
|
k
* fk |
3 |
38 |
69 |
84 |
30 |
24 |
14 |
8 |
9 |
279 |
3)По формуле
где
находим и заносим в строку fт
теоретические значения частот:
|
k |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
Σ |
|
fk |
3 |
19 |
23 |
21 |
6 |
4 |
2 |
1 |
1 |
80 |
|
k * fk |
3 |
38 |
69 |
84 |
30 |
24 |
14 |
8 |
9 |
279 |
|
fт |
8.53 |
14.88 |
17.29 |
15.08 |
10.52 |
6.11 |
3.05 |
1.33 |
0.51 |
|
4)Вычислим и занесем в строку таблицы
значения, стоящие в числителе выражения под знаком
суммы в формуле
для наблюдаемого значения критерия Пирсона:
|
k |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
Σ |
|
fk |
3 |
19 |
23 |
21 |
6 |
4 |
2 |
1 |
1 |
80 |
|
k * fk |
3 |
38 |
69 |
84 |
30 |
24 |
14 |
8 |
9 |
279 |
|
fт |
8.53 |
14.88 |
17.29 |
15.08 |
10.52 |
6.11 |
3.05 |
1.33 |
0.51 |
|
|
|
3.59 |
1.14 |
1.88 |
2.33 |
1.94 |
0.73 |
0.36 |
0.08 |
0.46 |
12,51 |
В результате получаем наблюдаемое значение .
5)По заданному уровню значимости α=0,05 и числу степеней
свободы ν = n-2, где n - число групп
в ряду (в нашем случае n=9) по
таблице значений критических точек распределения находим .
6)Поскольку (12,51 < 14,07) не отвергаем гипотезу о
том, что входящий поток описывается пуассоновским законом распределения с
интенсивностью λ=3,49 час-1.
Вид теоретической и экспериментальной зависимостей для
рассмотренного примера показан на построенной средствами Excel диаграмме:
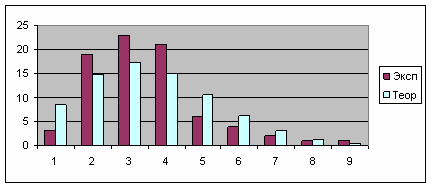
Пример анализа данных
наблюдения потока обслуживания.
Предположим, что проводилось наблюдение за временем
обслуживания клиентов отделения банка кассиром, в результате чего получена
таблица для частот интервалов следующего вида:
|
|
tмин |
tмакс |
f |
|
1 |
0 |
5 |
27 |
|
2 |
5 |
10 |
23 |
|
3 |
10 |
15 |
18 |
|
4 |
15 |
20 |
11 |
|
5 |
20 |
25 |
8 |
|
6 |
25 |
30 |
3 |
Определим среднее время и интенсивность μ обслуживания клиентов банка,
после чего обоснуем с уровнем значимости α=0,05 гипотезу о том, что время распределено по показательному закону,
используя для этого критерий Пирсона.
1)Находим среднее значение каждого временного интервала
по формуле:
Значения заносим в столбец, добавляемый к таблице
справа:
|
|
tмин |
tмакс |
f |
tср |
|
1 |
0 |
5 |
27 |
2.5 |
|
2 |
5 |
10 |
23 |
7.5 |
|
3 |
10 |
15 |
18 |
12.5 |
|
4 |
15 |
20 |
11 |
17.5 |
|
5 |
20 |
25 |
8 |
22.5 |
|
6 |
25 |
30 |
3 |
27.5 |
2)Находим среднее время
и интенсивность μ обслуживания
В приложении Excel среднее время удобно вычислять,
предварительно подсчитав в ячейках отдельного столбца входящие в выражение для
среднего времени произведения :
|
|
tмин |
tмакс |
f |
|
|
|
1 |
0 |
5 |
27 |
2.5 |
67.5 |
|
2 |
5 |
10 |
23 |
7.5 |
173 |
|
3 |
10 |
15 |
18 |
12.5 |
225 |
|
4 |
15 |
20 |
11 |
17.5 |
193 |
|
5 |
20 |
25 |
8 |
22.5 |
180 |
|
6 |
25 |
30 |
3 |
27.5 |
82.5 |
|
Σ |
|
|
90 |
|
|
3)По формуле
находим теоретические частоты:
|
|
tмин |
tмакс |
f |
|
|
fT |
|
1 |
0 |
5 |
27 |
2.5 |
67.5 |
34.82 |
|
2 |
5 |
10 |
23 |
7.5 |
173 |
21.35 |
|
3 |
10 |
15 |
18 |
12.5 |
225 |
13.09 |
|
4 |
15 |
20 |
11 |
17.5 |
193 |
8.03 |
|
5 |
20 |
25 |
8 |
22.5 |
180 |
4.92 |
|
6 |
25 |
30 |
3 |
27.5 |
82.5 |
3.02 |
|
Σ |
|
|
90 |
|
|
|
7)Вычислим и занесем в отдельный столбец таблицы
значения
,
входящие в выражение под знаком суммы в формуле
для наблюдаемого значения критерия Пирсона:
|
|
tмин |
tмакс |
f |
tср |
fT |
|
|
1 |
0 |
5 |
27 |
2.5 |
67.5 |
34.82 |
|
2 |
5 |
10 |
23 |
7.5 |
173 |
21.35 |
|
3 |
10 |
15 |
18 |
12.5 |
225 |
13.09 |
|
4 |
15 |
20 |
11 |
17.5 |
193 |
8.03 |
|
5 |
20 |
25 |
8 |
22.5 |
180 |
4.92 |
|
6 |
25 |
30 |
3 |
27.5 |
82.5 |
3.02 |
|
Σ |
|
|
90 |
|
|
6.75 |
В результате получаем .
4)По заданному уравнению значимости α=0,05 и числу
степеней свободы ν = n-2 , где n - число групп в ряду (в нашем случае n=6) в таблице значений критических
точек распределения находим .
5)Поскольку (6,75 < 9,49) не отвергаем гипотезу о том,
что время обслуживания клиентов описывается экспоненциальным законом
распределения с интенсивностью .
Вид теоретической и экспериментальной зависимостей для
рассмотренного примера показан на диаграмме:
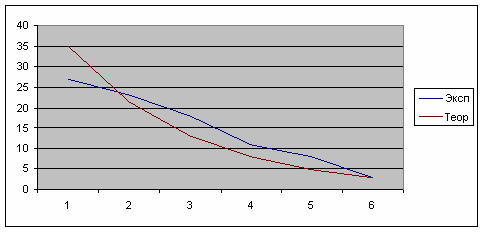
Задание.
В работе требуется:
1)Провести анализ данных наблюдения двух потоков в
системе массового обслуживания:
a) Входящего потока. Данные представляют собой число
появления требований в единицу времени.
b) Потока обслуживания. Данные представляют собой число
требований, обслуженных в интервале наблюдения.
Данные наблюдения входящего потока и потока
обслуживания приводятся в разделах 0 и 0 соответственно. Номером варианта служит порядковый
номер студента в списке группы.
2)Определить параметры потока (плотность и среднее время
интервала поступления или обслуживания заявок).
3)Дать заключение о возможности отнесения потока к
пуассоновскому потоку
Таблица χ2 приводится в разделе Ошибка! Источник ссылки не
найден..
4)Для каждого потока построить диаграммы с
теоретическими и экспериментальными значениями. Для входящего потока строится
гистограмма вероятности появления определенного числа требований в единицу
времени. Для выходящего потока (потока обслуживания) – график функции
распределения длительности обслуживания.
Работа выполняется с помощью табличного редактора
Microsoft Excel.
Отчет по
работе:
Отчет по работе должен включать:
- Исходные данные по каждому потоку,
- Промежуточные данные расчетов,
- Значения показателей потоков,
- Наблюдаемые и табличные значения χ2,
- Вывод о принятии/отбрасывании гипотезы пуассоновского
(экспоненциального) распределения,
- Диаграммы теоретических и экспериментальных значений.
Контрольные
вопросы:
1)Что такое пуассоновский поток?
2)Как записывается и что позволяет найти формула
Пуассона?
3)Как называется и что означает параметр пуассоновского закона?
4)Какому закону распределения подчиняются интервалы
между поступлением отдельных заявок потока?
5)Как найти вероятность того, что в течение
определенного интервала поступит не более определенного числа требований?
6)Чему равно математическое ожидание интервала времени
между событиями в пуассоновском потоке?
7)Чему равно среднеквадратическое отклонение интервала
времени между событиями в пуассоновском потоке?
8)В каких целях проводится аппроксимация
экспериментальных данных относительно потока заявок и времени обслуживания в
системе массового обслуживания теоретической зависимостью?
9)Из каких основных шагов состоит построение
теоретической зависимости?
10) Зачем нужно проводить оценку статистической значимости
результата?
11) Что будет являться результатом слияния двух
пуассоновских потоков?
12) Какие потоки получаются при ветвлении пуассоновского
потока на несколько потоков?
Задачи.
1)В бюро обслуживания поступает в среднем 12 заявок в
час. Считая поток заказов простейшим, определить вероятность того, что:
- за 1 минуту не поступит ни одного заказа,
- за 10 минут поступит не более трех заказов.
2)В ресторан, который начинает работать в 11.00,
прибывает в среднем 20 посетителей в час. Поток посетителей можно считать
простейшим. Требуется определить:
- вероятность того, что в 11.12 в ресторан придет 20
посетителей при условии, что в 11.07 их было 18,
- вероятность того, что между 11.28 и 11.30 в ресторане
окажется новый посетитель, если известно, что предшествующий посетитель прибыл
в 11.25.
3)На взлетно-посадочную полосу аэродрома прибывает
пуассоновский поток самолетов, в среднем 2 самолета за 5 минут. Найти
вероятность того, что в течение 15 минут произведут посадку 3 самолета.
4)Парикмахерская обслуживает в час 12 клиентов. В часы
пик в среднем приходит пять посетителей в час. Считая поток посетителей
простейшим, определить вероятность того, что клиента начнут обслуживать сразу.
5)Дан пуассоновский поток с параметром 2 мин-1. Найти
вероятность того, что длина интервала между соседними требованиями составляет
от 1 до 2 минут.
6)По железной дороге мимо наблюдателя движется в одном
направлении простейший поток поездов. Известно, что вероятность отсутствия
поездов в течение 10 минут равна 0,8. Требуется найти вероятность того, что за
20 мин мимо наблюдателя пройдет не более трех поездов.
7)По автостраде движется поток автомобилей,
подчиняющийся пуассоновскому распределению с параметром 1 мин-1. Найти
вероятность того, что длина интервала между соседними автомобилями составляет
от 2 до 4 минут.
8)В пункт текущего ремонта оргтехники поступают
требования на ремонт. Поток требований можно считать простейшим с
интенсивностью λ=0,307. Найти вероятность того, что за час не поступит ни
одного требования на ремонт.
9)Время обслуживания функциональных узлов некоторой системы
массового обслуживания распределено по показательному закону ,
где t - время в минутах. Найти вероятность того, что обслуживание продлится не
более 15 мин.
10) В пункт текущего ремонта вагонов метро поступают
требования на ремонт. Поток требований можно считать простейшим с
интенсивностью λ=0,617. Найти вероятность того, что за час поступит одно
требование (вагон) на ремонт.
11) Производится наложение (суперпозиция) двух простейших
потоков с интенсивностями и .
Будет ли поток, получившийся в результате наложения, простейшим, и если да, то
с какой интенсивностью?
12) Производится случайное прореживание простейшего потока
событий с интенсивностью ;
каждое событие, независимо от других, с вероятностью p сохраняется в потоке, а с вероятностью 1-р выбрасывается. Каким будет поток, получающийся в результате
прореживания простейшего потока?
13) Поток машин, идущих по шоссе в одном направлении,
представляет собой простейший поток с интенсивностью 2 машины в минуту. Человек
выходит на шоссе, чтобы остановить первую попавшуюся машину, идущую в данном
направлении. Найти закон распределения времени, в течение которого ему придется
ждать машину; математическое ожидание и среднее квадратичное отклонение времени
ожидания.
14) Компьютерный класс связан с каналом Интернет через
10-канальный концентратор. Интенсивности передачи данных по каждому из 10
каналов равны соответственно 540 бит/с, 120 бит/с, 40 бит/с, 170 бит/с, 350
бит/с, 60 бит/с, 742 бит/с, 153 бит/с, 500 бит/с, 100 бит/с. Поток данных
подчиняется пуассоновскому закону распределения. Определить интенсивность
передачи данных в канале Интернет.
15) Производится случайное прореживание простейшего потока
событий с интенсивностью ;
каждое событие, независимо от других, с вероятностью p=0,6 сохраняется в потоке, а с вероятностью 1-р выбрасывается. Каким будет поток, получающийся в результате
прореживания простейшего потока?
16) Поток машин, идущих по шоссе в одном направлении,
представляет собой простейший поток с интенсивностью 8 машин в минуту. Шоссе
имеет развилку в три направления. Вероятность движения машин в первом
направлении равна 0,12, во втором - 0,68, в третьем - 20. Определить
интенсивности движения автомобилей во всех направлениях.
17) Производится случайное прореживание простейшего потока
событий с интенсивностью ;
каждое событие, независимо от других, с вероятностью p=0,75 сохраняется в потоке, а с вероятностью 1-р выбрасывается. Каким будет поток, получающийся в результате
прореживания простейшего потока?
18) Производится разбиение случайного простейшего потока
событий с интенсивностью на три потока. Вероятности попадания событий в
тот или иной поток равны соответственно p1=0,2, p2=0,54, p3=0,26. Определить интенсивности каждого получившегося
потока в результате разбиения.
19) Производится разбиение случайного простейшего потока
событий с интенсивностью на 2 потока. Вероятности попадания событий в тот или иной поток соответственно равны
p1=0,44, p2=0,56.
Определить интенсивности каждого получившегося в результате разбиения потока.
20) Компьютерный класс связан с каналом Интернет через
5-канальный концентратор. Интенсивности передачи данных по каждому из 10
каналов равны соответственно 541 бит/с, 110 бит/с, 44 бит/с, 171 бит/с, 356
бит/с. Поток данных подчинятся пуассоновскому закону распределения. Определить
интенсивность передачи данных в канале Интернет.
Варианты данных наблюдения
Входящий поток.
Вариант №1
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1 |
4 |
5 |
4 |
3 |
5 |
5 |
3 |
7 |
|
2 |
7 |
4 |
3 |
3 |
2 |
4 |
5 |
5 |
|
3 |
7 |
3 |
1 |
5 |
8 |
5 |
6 |
3 |
|
4 |
2 |
7 |
4 |
5 |
6 |
3 |
2 |
3 |
|
5 |
5 |
2 |
5 |
2 |
1 |
3 |
2 |
4 |
|
6 |
4 |
4 |
2 |
2 |
4 |
4 |
2 |
1 |
|
7 |
3 |
4 |
5 |
4 |
1 |
5 |
2 |
4 |
|
8 |
5 |
1 |
5 |
7 |
3 |
4 |
5 |
5 |
|
9 |
7 |
4 |
3 |
4 |
7 |
4 |
4 |
3 |
|
10 |
3 |
5 |
5 |
2 |
4 |
3 |
3 |
5 |
Вариант №2
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1 |
2 |
3 |
6 |
3 |
5 |
11 |
6 |
4 |
|
2 |
3 |
4 |
5 |
4 |
3 |
8 |
4 |
2 |
|
3 |
2 |
3 |
4 |
5 |
4 |
5 |
6 |
5 |
|
4 |
4 |
5 |
3 |
10 |
5 |
3 |
4 |
2 |
|
5 |
3 |
2 |
9 |
5 |
4 |
4 |
5 |
3 |
|
6 |
5 |
3 |
5 |
12 |
5 |
3 |
2 |
7 |
|
7 |
2 |
5 |
8 |
4 |
7 |
5 |
6 |
4 |
Вариант №3
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1 |
1 |
3 |
7 |
3 |
5 |
11 |
6 |
4 |
|
2 |
3 |
5 |
5 |
4 |
10 |
8 |
4 |
2 |
|
3 |
2 |
4 |
4 |
5 |
4 |
5 |
6 |
5 |
|
4 |
5 |
5 |
3 |
10 |
5 |
3 |
4 |
2 |
|
5 |
3 |
2 |
8 |
5 |
4 |
4 |
5 |
3 |
|
6 |
5 |
3 |
5 |
11 |
5 |
4 |
2 |
7 |
|
7 |
2 |
5 |
8 |
4 |
7 |
5 |
6 |
4 |
|
8 |
1 |
4 |
8 |
9 |
7 |
10 |
6 |
5 |
|
9 |
3 |
5 |
2 |
4 |
8 |
5 |
6 |
4 |
Вариант №4
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1 |
3 |
1 |
8 |
3 |
3 |
7 |
5 |
4 |
|
2 |
5 |
3 |
5 |
4 |
9 |
5 |
4 |
2 |
|
3 |
4 |
2 |
3 |
5 |
4 |
4 |
6 |
5 |
|
4 |
5 |
5 |
4 |
10 |
5 |
3 |
4 |
2 |
|
5 |
2 |
3 |
4 |
5 |
4 |
8 |
5 |
3 |
|
6 |
3 |
5 |
5 |
11 |
5 |
5 |
2 |
7 |
|
7 |
5 |
2 |
10 |
4 |
7 |
8 |
6 |
4 |
|
8 |
4 |
1 |
11 |
9 |
7 |
8 |
6 |
5 |
Вариант №5
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1 |
1 |
2 |
0 |
5 |
1 |
1 |
2 |
2 |
|
2 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
|
3 |
1 |
3 |
1 |
2 |
0 |
1 |
1 |
2 |
|
4 |
1 |
0 |
3 |
1 |
0 |
1 |
3 |
4 |
|
5 |
1 |
1 |
2 |
1 |
2 |
6 |
1 |
1 |
|
6 |
0 |
1 |
2 |
1 |
2 |
0 |
1 |
1 |
|
7 |
0 |
0 |
4 |
1 |
0 |
1 |
3 |
4 |
Вариант №6
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1 |
2 |
4 |
6 |
1 |
2 |
2 |
0 |
5 |
|
2 |
1 |
1 |
1 |
1 |
0 |
1 |
2 |
1 |
|
3 |
3 |
1 |
7 |
2 |
5 |
1 |
0 |
1 |
|
4 |
1 |
1 |
1 |
1 |
0 |
1 |
2 |
2 |
|
5 |
1 |
3 |
3 |
1 |
2 |
2 |
2 |
2 |
|
6 |
4 |
4 |
2 |
1 |
3 |
2 |
2 |
1 |
|
7 |
1 |
1 |
2 |
1 |
0 |
0 |
3 |
5 |
Вариант №7
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1 |
0 |
2 |
0 |
2 |
2 |
4 |
2 |
1 |
|
2 |
2 |
3 |
3 |
2 |
1 |
2 |
1 |
4 |
|
3 |
1 |
2 |
1 |
1 |
1 |
5 |
4 |
1 |
|
4 |
3 |
2 |
2 |
1 |
2 |
2 |
0 |
1 |
|
5 |
1 |
4 |
2 |
2 |
0 |
1 |
0 |
2 |
|
6 |
2 |
7 |
2 |
3 |
1 |
0 |
2 |
6 |
|
7 |
1 |
6 |
1 |
1 |
2 |
2 |
1 |
1 |
|
8 |
3 |
3 |
3 |
1 |
2 |
0 |
2 |
2 |
Вариант №8
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1 |
2 |
0 |
4 |
1 |
3 |
2 |
4 |
5 |
|
2 |
2 |
0 |
2 |
3 |
3 |
2 |
1 |
2 |
|
3 |
2 |
5 |
4 |
0 |
5 |
0 |
1 |
2 |
|
4 |
6 |
4 |
1 |
3 |
6 |
5 |
3 |
4 |
|
5 |
8 |
3 |
3 |
2 |
3 |
4 |
0 |
7 |
|
6 |
1 |
2 |
3 |
4 |
3 |
3 |
0 |
2 |
|
7 |
2 |
3 |
4 |
7 |
0 |
2 |
2 |
2 |
|
8 |
4 |
1 |
3 |
5 |
0 |
4 |
3 |
3 |
Вариант №9
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1 |
3 |
2 |
1 |
2 |
0 |
1 |
5 |
2 |
|
2 |
3 |
7 |
3 |
4 |
2 |
7 |
3 |
3 |
|
3 |
2 |
2 |
3 |
6 |
3 |
4 |
3 |
5 |
|
4 |
5 |
4 |
4 |
2 |
6 |
5 |
6 |
2 |
|
5 |
4 |
2 |
1 |
6 |
2 |
3 |
1 |
5 |
|
6 |
3 |
1 |
3 |
6 |
6 |
5 |
3 |
2 |
|
7 |
4 |
3 |
5 |
2 |
5 |
3 |
5 |
1 |
|
8 |
7 |
3 |
8 |
3 |
4 |
8 |
4 |
2 |
Вариант №10
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1 |
3 |
2 |
1 |
2 |
0 |
1 |
5 |
2 |
|
2 |
3 |
7 |
3 |
4 |
2 |
7 |
3 |
3 |
|
3 |
2 |
2 |
3 |
6 |
3 |
4 |
3 |
5 |
|
4 |
5 |
4 |
4 |
2 |
6 |
5 |
6 |
2 |
|
5 |
4 |
2 |
1 |
6 |
2 |
3 |
1 |
5 |
|
6 |
3 |
1 |
3 |
6 |
6 |
5 |
3 |
2 |
|
7 |
4 |
3 |
5 |
2 |
5 |
3 |
5 |
1 |
|
8 |
7 |
3 |
8 |
3 |
4 |
8 |
4 |
2 |
Вариант №11
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1 |
6 |
2 |
4 |
4 |
4 |
5 |
2 |
6 |
|
2 |
1 |
1 |
3 |
4 |
3 |
3 |
3 |
4 |
|
3 |
0 |
1 |
6 |
2 |
3 |
3 |
2 |
3 |
|
4 |
4 |
1 |
5 |
4 |
2 |
5 |
2 |
2 |
|
5 |
4 |
1 |
4 |
4 |
3 |
4 |
3 |
4 |
|
6 |
4 |
4 |
3 |
3 |
2 |
3 |
3 |
3 |
|
7 |
1 |
3 |
6 |
2 |
2 |
1 |
3 |
2 |
|
8 |
3 |
2 |
2 |
3 |
1 |
2 |
2 |
3 |
Вариант №12
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1 |
2 |
1 |
4 |
5 |
1 |
2 |
7 |
2 |
|
2 |
1 |
2 |
3 |
2 |
2 |
5 |
1 |
0 |
|
3 |
2 |
0 |
2 |
3 |
2 |
4 |
1 |
6 |
|
4 |
0 |
4 |
2 |
4 |
6 |
2 |
1 |
1 |
|
5 |
2 |
2 |
2 |
4 |
1 |
5 |
2 |
1 |
|
6 |
4 |
1 |
1 |
2 |
4 |
2 |
1 |
3 |
|
7 |
4 |
2 |
3 |
1 |
2 |
2 |
2 |
1 |
|
8 |
0 |
1 |
1 |
2 |
1 |
0 |
2 |
1 |
Вариант №13
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1 |
1 |
4 |
4 |
5 |
2 |
3 |
5 |
1 |
|
2 |
2 |
5 |
7 |
1 |
1 |
3 |
1 |
5 |
|
3 |
2 |
1 |
6 |
1 |
4 |
1 |
4 |
1 |
|
4 |
3 |
2 |
4 |
1 |
1 |
1 |
3 |
2 |
|
5 |
5 |
2 |
5 |
4 |
1 |
1 |
2 |
3 |
|
6 |
2 |
3 |
5 |
3 |
2 |
2 |
6 |
2 |
|
7 |
1 |
5 |
1 |
2 |
0 |
3 |
1 |
0 |
|
8 |
1 |
3 |
1 |
3 |
3 |
2 |
2 |
2 |
Вариант №14
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1 |
1 |
2 |
2 |
4 |
3 |
1 |
2 |
2 |
|
2 |
2 |
3 |
1 |
1 |
3 |
1 |
2 |
3 |
|
3 |
2 |
2 |
3 |
3 |
4 |
2 |
1 |
2 |
|
4 |
2 |
5 |
1 |
0 |
1 |
1 |
5 |
1 |
|
5 |
2 |
2 |
0 |
2 |
2 |
2 |
2 |
2 |
|
6 |
1 |
3 |
3 |
1 |
0 |
0 |
0 |
1 |
|
7 |
1 |
1 |
3 |
1 |
0 |
0 |
4 |
4 |
|
8 |
1 |
2 |
2 |
2 |
3 |
3 |
2 |
2 |
Вариант №15
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1 |
1 |
2 |
0 |
3 |
2 |
2 |
2 |
0 |
|
2 |
2 |
2 |
3 |
1 |
3 |
0 |
1 |
3 |
|
3 |
3 |
1 |
5 |
3 |
0 |
1 |
0 |
5 |
|
4 |
1 |
2 |
1 |
2 |
1 |
3 |
3 |
1 |
|
5 |
2 |
3 |
1 |
5 |
3 |
5 |
3 |
0 |
|
6 |
1 |
4 |
1 |
1 |
3 |
3 |
2 |
1 |
|
7 |
2 |
1 |
3 |
2 |
1 |
4 |
2 |
3 |
|
8 |
3 |
2 |
2 |
1 |
1 |
0 |
3 |
2 |
Вариант №16
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1 |
2 |
2 |
3 |
5 |
4 |
2 |
5 |
2 |
|
2 |
2 |
0 |
2 |
2 |
2 |
1 |
2 |
1 |
|
3 |
1 |
3 |
1 |
0 |
1 |
2 |
5 |
2 |
|
4 |
2 |
2 |
0 |
4 |
1 |
1 |
1 |
2 |
|
5 |
1 |
0 |
3 |
1 |
3 |
2 |
1 |
0 |
|
6 |
1 |
3 |
2 |
4 |
4 |
2 |
2 |
0 |
|
7 |
2 |
3 |
2 |
3 |
5 |
4 |
0 |
3 |
|
8 |
5 |
2 |
1 |
2 |
3 |
6 |
5 |
1 |
Вариант №17
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1 |
3 |
2 |
1 |
2 |
2 |
4 |
3 |
2 |
|
2 |
0 |
3 |
2 |
2 |
1 |
3 |
3 |
1 |
|
3 |
3 |
2 |
1 |
0 |
2 |
0 |
3 |
1 |
|
4 |
6 |
0 |
1 |
2 |
2 |
0 |
0 |
1 |
|
5 |
0 |
1 |
2 |
1 |
2 |
3 |
0 |
2 |
|
6 |
0 |
1 |
2 |
1 |
2 |
2 |
2 |
0 |
|
7 |
1 |
4 |
1 |
1 |
0 |
1 |
1 |
1 |
|
8 |
6 |
3 |
3 |
3 |
2 |
3 |
2 |
0 |
Вариант №18
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1 |
2 |
6 |
3 |
3 |
1 |
3 |
2 |
1 |
|
2 |
3 |
1 |
5 |
4 |
1 |
4 |
2 |
1 |
|
3 |
1 |
4 |
1 |
2 |
2 |
4 |
1 |
0 |
|
4 |
1 |
2 |
3 |
2 |
0 |
2 |
1 |
2 |
|
5 |
0 |
2 |
2 |
1 |
3 |
4 |
2 |
2 |
|
6 |
2 |
3 |
3 |
2 |
2 |
2 |
7 |
4 |
|
7 |
2 |
1 |
3 |
2 |
4 |
2 |
5 |
1 |
|
8 |
1 |
1 |
1 |
8 |
6 |
1 |
3 |
2 |
Вариант №19
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1 |
3 |
4 |
0 |
3 |
3 |
2 |
4 |
4 |
|
2 |
3 |
2 |
2 |
6 |
6 |
0 |
2 |
1 |
|
3 |
2 |
2 |
6 |
3 |
0 |
2 |
0 |
4 |
|
4 |
2 |
3 |
4 |
1 |
4 |
1 |
2 |
2 |
|
5 |
3 |
2 |
1 |
3 |
2 |
0 |
5 |
4 |
|
6 |
3 |
2 |
2 |
3 |
2 |
0 |
5 |
1 |
|
7 |
2 |
4 |
3 |
2 |
4 |
4 |
7 |
3 |
|
8 |
2 |
3 |
0 |
2 |
8 |
3 |
2 |
1 |
Вариант №20
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1 |
3 |
3 |
5 |
3 |
5 |
3 |
3 |
3 |
|
2 |
3 |
4 |
3 |
2 |
4 |
1 |
5 |
2 |
|
3 |
1 |
4 |
4 |
2 |
2 |
4 |
4 |
4 |
|
4 |
2 |
2 |
4 |
2 |
2 |
1 |
3 |
2 |
|
5 |
1 |
4 |
3 |
1 |
2 |
3 |
2 |
3 |
|
6 |
2 |
3 |
4 |
3 |
4 |
4 |
3 |
4 |
|
7 |
2 |
2 |
2 |
3 |
0 |
5 |
3 |
4 |
|
8 |
6 |
3 |
6 |
4 |
5 |
3 |
4 |
3 |
Вариант №21
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1 |
4 |
3 |
5 |
3 |
5 |
3 |
4 |
1 |
|
2 |
2 |
3 |
4 |
3 |
4 |
3 |
2 |
5 |
|
3 |
6 |
5 |
2 |
2 |
2 |
1 |
5 |
7 |
|
4 |
5 |
7 |
5 |
3 |
2 |
5 |
5 |
3 |
|
5 |
0 |
3 |
9 |
4 |
6 |
3 |
1 |
7 |
|
6 |
1 |
2 |
5 |
7 |
2 |
3 |
4 |
3 |
|
7 |
5 |
5 |
3 |
3 |
3 |
4 |
4 |
8 |
|
8 |
5 |
4 |
6 |
3 |
1 |
9 |
5 |
9 |
Вариант №22
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1 |
3 |
2 |
2 |
5 |
4 |
3 |
1 |
6 |
|
2 |
1 |
2 |
2 |
0 |
1 |
1 |
2 |
2 |
|
3 |
4 |
2 |
1 |
5 |
3 |
1 |
0 |
3 |
|
4 |
7 |
6 |
2 |
4 |
2 |
1 |
4 |
0 |
|
5 |
3 |
2 |
4 |
5 |
2 |
4 |
4 |
5 |
|
6 |
2 |
6 |
1 |
2 |
1 |
3 |
2 |
4 |
|
7 |
4 |
7 |
3 |
1 |
6 |
3 |
2 |
6 |
|
8 |
4 |
1 |
2 |
2 |
1 |
3 |
0 |
4 |
Вариант №23
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1 |
3 |
1 |
2 |
2 |
1 |
1 |
2 |
0 |
|
2 |
1 |
6 |
3 |
1 |
7 |
2 |
1 |
1 |
|
3 |
5 |
3 |
4 |
3 |
3 |
2 |
1 |
3 |
|
4 |
2 |
1 |
3 |
2 |
1 |
4 |
3 |
4 |
|
5 |
3 |
4 |
4 |
1 |
1 |
5 |
0 |
4 |
|
6 |
3 |
1 |
3 |
3 |
2 |
0 |
5 |
3 |
|
7 |
5 |
4 |
5 |
1 |
3 |
0 |
1 |
1 |
|
8 |
6 |
4 |
2 |
4 |
5 |
5 |
1 |
4 |
Вариант №24
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1 |
1 |
3 |
0 |
1 |
3 |
1 |
0 |
0 |
|
2 |
1 |
2 |
1 |
1 |
1 |
4 |
0 |
1 |
|
3 |
5 |
4 |
7 |
1 |
6 |
0 |
2 |
5 |
|
4 |
3 |
1 |
2 |
2 |
1 |
3 |
3 |
2 |
|
5 |
2 |
4 |
5 |
2 |
1 |
0 |
2 |
4 |
|
6 |
2 |
1 |
5 |
2 |
3 |
1 |
0 |
5 |
|
7 |
0 |
2 |
2 |
1 |
4 |
2 |
3 |
2 |
|
8 |
0 |
2 |
6 |
1 |
8 |
1 |
2 |
3 |
Вариант №25
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1 |
2 |
1 |
2 |
3 |
1 |
4 |
3 |
1 |
|
2 |
4 |
5 |
5 |
2 |
2 |
2 |
2 |
0 |
|
3 |
2 |
2 |
5 |
2 |
3 |
0 |
2 |
3 |
|
4 |
5 |
4 |
2 |
1 |
2 |
0 |
3 |
2 |
|
5 |
2 |
5 |
3 |
2 |
1 |
2 |
0 |
0 |
|
6 |
4 |
2 |
1 |
3 |
2 |
2 |
4 |
2 |
|
7 |
2 |
5 |
1 |
3 |
4 |
4 |
3 |
4 |
|
8 |
3 |
0 |
0 |
3 |
2 |
1 |
4 |
2 |
Поток обслуживания.
Вариант №1
|
|
tмин |
tмакс |
f |
|
1 |
0,00 |
1,87 |
50 |
|
2 |
1,87 |
3,74 |
17 |
|
3 |
3,74 |
5,60 |
20 |
|
4 |
5,60 |
7,46 |
8 |
|
5 |
7,46 |
9,32 |
3 |
|
6 |
9,32 |
11,18 |
1 |
Вариант №2
|
|
tмин |
tмакс |
f |
|
1 |
0,00 |
8,60 |
98 |
|
2 |
8,60 |
17,20 |
43 |
|
3 |
17,20 |
25,80 |
5 |
|
4 |
25,80 |
34,40 |
3 |
|
5 |
34,40 |
43,00 |
1 |
|
6 |
43,00 |
51,60 |
1 |
Вариант №3
|
|
tмин |
tмакс |
f |
|
1 |
0,00 |
9,52 |
94 |
|
2 |
9,52 |
19,05 |
38 |
|
3 |
19,05 |
28,57 |
10 |
|
4 |
28,57 |
38,09 |
3 |
|
5 |
38,09 |
47,62 |
2 |
|
6 |
47,62 |
57,14 |
3 |
Вариант №4
|
|
tмин |
tмакс |
f |
|
1 |
0,00 |
5,29 |
170 |
|
2 |
5,29 |
10,58 |
64 |
|
3 |
10,58 |
15,87 |
20 |
|
4 |
15,87 |
21,16 |
6 |
|
5 |
21,16 |
26,45 |
3 |
|
6 |
26,45 |
31,75 |
3 |
Вариант №5
|
|
tмин |
tмакс |
f |
|
1 |
0,00 |
6,35 |
144 |
|
2 |
6,35 |
12,70 |
49 |
|
3 |
12,70 |
19,05 |
14 |
|
4 |
19,05 |
25,40 |
4 |
|
5 |
25,40 |
31,75 |
2 |
|
6 |
31,75 |
38,09 |
3 |
Вариант №6
|
|
tмин |
tмакс |
f |
|
1 |
0,00 |
11,64 |
142 |
|
2 |
11,64 |
23,28 |
44 |
|
3 |
23,28 |
34,92 |
16 |
|
4 |
34,92 |
46,56 |
5 |
|
5 |
46,56 |
58,20 |
3 |
|
6 |
58,20 |
69,84 |
3 |
Вариант №7
|
|
tмин |
tмакс |
f |
|
1 |
0,00 |
12,70 |
224 |
|
2 |
12,70 |
25,40 |
76 |
|
3 |
25,40 |
38,09 |
43 |
|
4 |
38,09 |
50,79 |
8 |
|
5 |
50,79 |
63,49 |
4 |
|
6 |
63,49 |
76,19 |
3 |
Вариант №8
|
|
tмин |
tмакс |
f |
|
1 |
0,00 |
15,87 |
212 |
|
2 |
15,87 |
31,75 |
56 |
|
3 |
31,75 |
47,62 |
29 |
|
4 |
47,62 |
63,49 |
9 |
|
5 |
63,49 |
79,36 |
4 |
|
6 |
79,36 |
95,24 |
3 |
Вариант №9
|
|
tмин |
tмакс |
f |
|
1 |
0,00 |
8,47 |
124 |
|
2 |
8,47 |
16,93 |
70 |
|
3 |
16,93 |
25,40 |
33 |
|
4 |
25,40 |
33,86 |
7 |
|
5 |
33,86 |
42,33 |
3 |
|
6 |
42,33 |
50,79 |
3 |
Вариант №10
|
|
tмин |
tмакс |
f |
|
1 |
0,00 |
4,65 |
39 |
|
2 |
4,65 |
9,31 |
16 |
|
3 |
9,31 |
13,96 |
7 |
|
4 |
13,96 |
18,62 |
1 |
|
5 |
18,62 |
23,27 |
0 |
|
6 |
23,27 |
27,93 |
1 |
Вариант №11
|
|
tмин |
tмакс |
f |
|
1 |
0,00 |
7,94 |
89 |
|
2 |
7,94 |
15,87 |
38 |
|
3 |
15,87 |
23,81 |
10 |
|
4 |
23,81 |
31,75 |
3 |
|
5 |
31,75 |
39,68 |
2 |
|
6 |
39,68 |
47,62 |
3 |
Вариант №12
|
|
tмин |
tмакс |
f |
|
1 |
0,00 |
5,82 |
137 |
|
2 |
5,82 |
11,64 |
49 |
|
3 |
11,64 |
17,46 |
17 |
|
4 |
17,46 |
23,28 |
6 |
|
5 |
23,28 |
29,10 |
3 |
|
6 |
29,10 |
34,92 |
3 |
Вариант №13
|
|
tмин |
tмакс |
f |
|
1 |
0,00 |
6,24 |
142 |
|
2 |
6,24 |
12,49 |
48 |
|
3 |
12,49 |
18,73 |
16 |
|
4 |
18,73 |
24,97 |
4 |
|
5 |
24,97 |
31,22 |
3 |
|
6 |
31,22 |
37,46 |
3 |
Вариант №14
|
|
tмин |
tмакс |
f |
|
1 |
0,00 |
16,72 |
131 |
|
2 |
16,72 |
33,44 |
54 |
|
3 |
33,44 |
50,16 |
31 |
|
4 |
50,16 |
66,88 |
4 |
|
5 |
66,88 |
83,60 |
3 |
|
6 |
83,60 |
100,32 |
3 |
Вариант №15
|
|
tмин |
tмакс |
f |
|
1 |
0,00 |
4,97 |
172 |
|
2 |
4,97 |
9,95 |
51 |
|
3 |
9,95 |
14,92 |
18 |
|
4 |
14,92 |
19,89 |
6 |
|
5 |
19,89 |
24,87 |
4 |
|
6 |
24,87 |
29,84 |
3 |
Вариант №16
|
|
tмин |
tмакс |
f |
|
1 |
0,00 |
14,83 |
42 |
|
2 |
14,83 |
29,66 |
18 |
|
3 |
29,66 |
44,49 |
1 |
|
4 |
44,49 |
59,32 |
1 |
|
5 |
59,32 |
74,15 |
1 |
|
6 |
74,15 |
88,98 |
1 |
Вариант №17
|
|
tмин |
tмакс |
f |
|
1 |
0,00 |
7,93 |
30 |
|
2 |
7,93 |
15,86 |
17 |
|
3 |
15,86 |
23,78 |
10 |
|
4 |
23,78 |
31,71 |
6 |
|
5 |
31,71 |
39,64 |
0 |
|
6 |
39,64 |
47,57 |
1 |
Вариант №18
|
|
tмин |
tмакс |
f |
|
1 |
0,00 |
4,06 |
36 |
|
2 |
4,06 |
8,11 |
16 |
|
3 |
8,11 |
12,17 |
4 |
|
4 |
12,17 |
16,23 |
6 |
|
5 |
16,23 |
20,28 |
1 |
|
6 |
20,28 |
24,34 |
1 |
Вариант №19
|
|
tмин |
tмакс |
f |
|
1 |
0,00 |
8,74 |
34 |
|
2 |
8,74 |
17,47 |
17 |
|
3 |
17,47 |
26,21 |
5 |
|
4 |
26,21 |
34,95 |
4 |
|
5 |
34,95 |
43,69 |
2 |
|
6 |
43,69 |
52,42 |
2 |
Вариант №20
|
|
tмин |
tмакс |
f |
|
1 |
0,00 |
10,14 |
49 |
|
2 |
10,14 |
20,28 |
9 |
|
3 |
20,28 |
30,41 |
6 |
|
4 |
30,41 |
40,55 |
2 |
|
5 |
40,55 |
50,69 |
0 |
|
6 |
50,69 |
60,83 |
1 |
Вариант №21
|
|
tмин |
tмакс |
f |
|
1 |
0,00 |
7,76 |
33 |
|
2 |
7,76 |
15,52 |
12 |
|
3 |
15,52 |
23,28 |
11 |
|
4 |
23,28 |
31,04 |
5 |
|
5 |
31,04 |
38,80 |
2 |
|
6 |
38,80 |
46,56 |
1 |
Вариант №22
|
|
tмин |
tмакс |
f |
|
1 |
0,00 |
9,44 |
37 |
|
2 |
9,44 |
18,89 |
20 |
|
3 |
18,89 |
28,33 |
5 |
|
4 |
28,33 |
37,78 |
0 |
|
5 |
37,78 |
47,22 |
1 |
|
6 |
47,22 |
56,67 |
1 |
Вариант №23
|
|
tмин |
tмакс |
f |
|
1 |
0,00 |
3,55 |
22 |
|
2 |
3,55 |
7,09 |
20 |
|
3 |
7,09 |
10,64 |
12 |
|
4 |
10,64 |
14,18 |
6 |
|
5 |
14,18 |
17,73 |
2 |
|
6 |
17,73 |
21,27 |
2 |
Вариант №24
|
|
tмин |
tмакс |
f |
|
1 |
0,00 |
7,75 |
42 |
|
2 |
7,75 |
15,50 |
12 |
|
3 |
15,50 |
23,25 |
4 |
|
4 |
23,25 |
31,01 |
2 |
|
5 |
31,01 |
38,76 |
0 |
|
6 |
38,76 |
46,51 |
1 |
Вариант №25
|
|
tмин |
tмакс |
f |
|
1 |
0,00 |
2,72 |
28 |
|
2 |
2,72 |
5,44 |
17 |
|
3 |
5,44 |
8,15 |
5 |
|
4 |
8,15 |
10,87 |
6 |
|
5 |
10,87 |
13,59 |
6 |
|
6 |
13,59 |
16,31 |
2 |