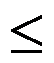1.1. ЭТАПЫ ИССЛЕДОВАНИЯ ОПЕРАЦИЙ

Усложнение производства, техники и организационной структу­ры общества приводит к тому, что принятие решений и эффективное руководство все больше и больше нуждаются в широкой, точной и быстрой информации, количественной оценке и прогнозе результатов, последствий принятых решений. Назначение методов исследования операций - объективно разобраться в каждом явлении, численно оце­нить предлагаемые целенаправленные действия и, возможно, пред­ложить варианты решений, отличные от тех, которые рассматривали хозяйственные или другие руководители.

Несмотря на многообразие задач, возникающих в экономике (задача оптимального планирования инвестиций, формирование минимальной потребительской корзины, организация рекламной деятельности, составление штатного расписания, определение специализации предприятия и т.д.), при их решении можно выделить некоторую общую последовательность этапов, через которые проходит любое операционное исследование.

Как правило, это:

1. Постановка задачи.

2. Построение содержательной (вербальной) модели рассматриваемого объекта (операции, процесса). На данном этапе происходит формализация цели управления объектом, выделение возможных управляющих воздействий, влияющих на достижение сформулированной цели, а также описание системы ограничений на управляющие воздействия.

3. Построение математической модели, т.е. перевод сконструированной вербальной модели в ту форму, в которой для ее изучения может быть использован математический аппарат.

4. Анализ модели или получение решения задачи. 

5. Анализ решения, т.е. получение информации об изменениях решения при изменении условий (неуправляемых переменных) функционированиясистемы. Эту часть исследования обычно называют анализом модели на чувствитель­ность.

6. Проверка полученных результатов на их адекватность природе изучаемой системы, включая исследование влияния так называемых внемодельных факторов, и возможная корректировка первоначальной модели.

Реализация полученного решения на практике.

 

Краткое описание каждого этапа (Л 3, 4, 8)

 

1,2) Постановка задачи является одним из наиболее важных эта­пов исследования операций. При постановке зада­чи исследования операций необходимо определить цель, преследуемую субъектом управления (ЛПР) и установить,значениекаких характеристик (управляемых переменных) исследуемой системы (процесса) можно варьировать, а изменение значений каких перемен­ных (неуправляемых) не зависит от решений ЛПР. Кроме того, на данном этапе необходимо определить требования, условия и ограничения на исследуемую операцию. На этом же этапе должны быть решены проблемы информационного обеспечения будущей модели ИО.

3) Построение модели. На этом этапе необходимо выбрать модель, наиболее подходящую для адекватного описания ИО. При построении модели должны быть установлены количественные соотношения для выражения  целевой функции (ЦФ) и ограничений в виде функций от управляемых переменных.  Наиболее важным типом моделей ИО являются математические модели (ММ). В основеих построения лежитдопущение о том, что все переменные, ограничения,их связывающие, а также целевая функция количественно измеримы. Поэтому если  X_j,  j = 1, n представляют собой  n уп­равляемых переменных, а условия функционирования исследуемой системы (ИС)  характеризуются  m ограничениями, то ММ может быть записана в следующем виде:

¦(x₁, x₂ … x_n) àmax, min       –  целевая функция

g_i(x₁, x₂ … x_n) ≤ b_i, i = 1, m      – ограничения

4) Анализ модели обычно производится с помощью методов математического программирования.

5) Анализ решения или анализ на чувствительность – это процесс, реализуемый после того,  как оптимальное решение задачи получено. В рамках такого анализа выявляется чувствительность оптимального  решения к определенным изменениям исходной модели, т.е. фактически рассматривается совокупность моделей, что придает исследуемой операции определенную динамичность.

6) Решение, полученное при помощи анализа модели, не может, однако, не­посредственно быть рекомендовало для практической реализации. Ма­тематическая модель, как и любая другая модель, лишь частично ото­бражает действительность, акцентирует отдельные ее аспекты. Адек­ватность модели исследуемой операции и, следовательно, качество полученного результата можно проверить, сопоставлял результаты, установленные без использования модели, с результатами, вытекающими из анализа модели.

7) Работы по исследованию операций имеют смысл, если они завер­шаются внедрением результатов исследования в практику. Важность задач координации научной и производственной деятельности и труд­ности, связанные с внедрением научных рекомендаций в производство, заставляют рассматривать эти вопросы как отдельный этап в иссле­довании операций. При этом следует помнить, что задача исследова­теля операции - подготовить решение, а не принять его. Руководи­тель, ответственный за решение, должен учитывать помимо рекомен­даций исследователя операций, основанных на количественных оцен­ках, и другие факторы, не поддающиеся формализации.

В исследовании операций используется разнообразный математи­ческий аппарат. Чаще других методов для анализа моделей операций и подготовки решений используются методы математического програм­мирования, комбинаторного анализа и статистического моделирования.

Математическое программирование - область математики, разраба­тывающая теорию и численные методы решения многомерных экстремаль­ных задач с ограничениями, т.е. задач на экстремум функции многих переменных с ограничениями на область  изменения этих переменных.

Задача математического программирования (ЗМП) имеет вид:

(1)

¦(x₁, x₂ … x_n) àmax, min       –  целевая функция

g_i(x₁, x₂ … x_n) ≤ b_i, i = 1, m      – ограничения

В зависимости от свойств функций ¦ и g_i математическое про­граммирование можно рассматривать как ряд самостоятельных дисциплин, занимающихся изучением и разработкой методов ре­шения определенных классов задач.

Прежде всего, задачи математического программирования делятся на задачи линейного и нелинейного программирования. При этом если все функции ¦ и g_i линейные, то соответствующая задача является задачей линейного программирования. Если же хотя бы одна из указанных функций нелинейная, то соответ­ствующая задача является задачей нелинейного программиро­вания.

Наиболее изученным разделом математического программи­рования является линейное программирование. Для решения задач линейного программирования разработан целый ряд эффективных методов, алгоритмов и программ.

Среди задач нелинейного программирования наиболее глу­боко изучены задачи выпуклого программирования. Это задачи, в результате решения которых определяется минимум выпуклой (или максимум вогнутой) функции, заданной на выпуклом зам­кнутом множестве.

В свою очередь, среди задач выпуклого программирования более подробно исследованы задачи квадратичного программи­рования. В результате решения таких задач требуется в общем случае найти максимум (или минимум) квадратичной функции при условии, что ее переменные удовлетворяют некоторой системе линейных неравенств или линейных уравнений, либо некоторой системе, содержащей как линейные неравенства, так и линей­ные уравнения.

Отдельными классами задач математического программи­рования являются задачи целочисленного, параметрического и дробно-линейного программирования.

В задачах целочисленного программирования неизвестные могут принимать только целочисленные значения.

В задачах параметрического программирования целевая функция или функции, определяющие область возможных изме­нений переменных, либо то и другое зависят от некоторых пара­метров.

В задачах дробно-линейного программирования целевая функция представляет собой отношение двух линейных функ­ций, а функции, определяющие область возможных изменений переменных, также являются линейными.

Выделяют отдельные классы задач стохастического и дина­мического программирования.

Если в целевой функции или в функциях, определяющих об­ласть возможных изменений переменных, содержатся случай­ные величины, то такая задача относится к задаче стохастиче­ского программирования.

Задача, процесс нахождения решения которой является мно­гоэтапным, относится к задаче динамического программирова­ния.

Рассмотрим несколько примеров проведения операционного исследования.

Пример 1.1. Фабрика выпускает продукцию двух видов: П₁ и П₂. Продукция обоих видов поступает в оптовую продажу. Для производства этой продукции используются три исходных продукта - A, B, C. Максимально возможные суточные запасы этих продуктов составляют 6, 8 и 5 т соответственно. Расходы сырья A, B, C на 1 тыс. изделий П₁ и П₂ приведены в табл. 1.1

 

Таблица 1.1

 

 

Изучение рынка сбыта показало, что суточный спрос на изделия П₂ никогда не превышает спроса изделия П₁ более чем на 1 тыс. шт. Кроме того, установлено, что спрос на изделия П₂ никогда не превышает  2 тыс. шт. в сутки.

Оптовые цены 1 тыс. шт. изделий П₁ равны 3 тыс. руб.,    1 тыс. шт. П₂ - 2 тыс. шт.

Какое количество изделий (в тыс. шт.) каждого вида должна производить фабрика, чтобы доход от реализации продукции был максимальным?

Построение математической модели следует начать с идентификации переменных (искомых величин). После этого целевая функция и ограничения выражаются через соответствующие переменные.

В рассматриваемом примере имеем следующее:

Переменные. Так как нужно определить объемы производства каждого вида продукции, переменными являются:

X₁ - суточный объем производства изделия П₁ в тыс. шт.;

X₂ - суточный объем производства изделия П₂ в тыс. шт.

 

Целевая функция. Так как стоимость 1 тыс. изделий П₁ равна 3 тыс. руб., суточный доход от ее продажи составит 3X₁ тыс. руб. Аналогично доход от реализации X₂ тыс. шт. П₂ составит 2X₂ тыс. руб. в сутки. При допущении независимости объемов сбыта каждого из изделий общий доход равен сумме двух слагаемых - дохода от продажи изделий П₁ и дохода от продажи изделий П₂.

Обозначив доход (в тыс. руб.) через , можно дать следующую математическую формулировку целевой функции: определить (допустимые) значения X₁ и X₂ , максимизирующие величину общего дохода:

 ,

 

Ограничения. При решении рассматриваемой задачи должны быть учтены ограничения на расход исходных продуктов A, B и С и спрос на изготовляемую продукцию, что можно записать так:

 

 

Это приводит к трем ограничениям:

 

X₁   +  2X₂  6   (для А),

2X₁   +   X₂   8   (для В),

X₁ + 0.8X₂   5   (для С).

 

Ограничения на величину спроса на продукцию имеют вид:

X₂ - X₁  1  (соотношение величин спроса на изделия П₁ и П₂),

X₂   2  (максимальная величина спроса на изделия П₂).

 

Вводятся также условия неотрицательности переменных, т. е. ограничения на их знак:

X₁  0  (объем производства П₁),

X₂  0  (объем производства П₂).

 

Эти ограничения заключаются в том, что объемы производства продукции не могут принимать отрицательных значений.

Следовательно, математическая модель записывается следующим образом.

Определить суточные объемы производства (Х₁ и Х₂) изделий П₁ и П₂ в тыс. шт., при которых достигается

 

     (целевая функция)                                          

при

 Х₁ +    2Х₂   6

2X₁ +     X₂   8

 X₁ +  0.8X₂  5             ограничения                             (1.1)

      -X₁ + Х₂   1

              X₂   2

X₁  0 ,   X₂  0

 

Пример 1.2. Металлургическому заводу требуется уголь с содержанием фосфора не более 0.03% и с долей зольных примесей не более 3.25%. Завод закупает три сорта угля А, В, С с известным содержанием примесей. В какой пропорции нужно смешивать исходные продукты А, В, С, чтобы смесь удовлетворяла ограничениям на содержание примесей и имела минимальную цену?

Содержание примесей и цена исходных продуктов приведены в табл. 1.2.

 

Таблица 1.2

 

 

Построим математическую модель.

Обозначим:

Х₁ - количество угля сорта А в тонне смеси

Х₂ - количество угля сорта В в тонне смеси             переменные

Х₃ - количество угля сорта С в тонне смеси                 модели

 

 - стоимость 1 т смеси -целевая функция,

0.06Х₁ + 0.04Х₂ + 0.02Х₃  0.03 (%) - ограничение на содержание фосфора в смеси,

2Х₁ + 4Х₂ + 3Х₃   3.25 (%) - ограничение на содержание зольных примесей,

Х₁ + Х₂ + Х₃ = 1 (т) - ограничение на состав 1 т смеси.

Окончательно, математическая модель имеет вид.

Определить количество угля сортов А, В, С (Х₁, Х₂, Х₃) в тонне смеси, при которых достигается

при

0.06Х₁ + 0.04Х₂ + 0.02Х₃  0.03

2Х₁ + 4Х₂ + 3Х₃   3.25                                                   (1.2)

Х₁ + Х₂ + Х₃ = 1

Х_1,2,3   0.

 

Пример1.3. (задача составления кормовой смеси или задача о диете).

Бройлерное хозяйство птицеводческой фермы насчитывает 20 000 цыплят, которые выращиваются до 8-недельного возраста и после соответствующей обработки поступают в продажу. Недельный расход корма в среднем (за 8 недель) составляет 500г = 0.5 кг.

Для того, чтобы цыплята достигли к 8-й неделе необходимого веса, кормовой рацион должен удовлетворять определенным требованиям по питательности. Этим требованиям могут соответствовать смеси различных видов кормов, или ингредиентов.

В табл. 3 приведены данные, характеризующие содержание (по весу) питательных веществ в каждом из ингредиентов и удельную стоимость каждого ингредиента. Смесь должна содержать:

не менее 0.8% кальция

не менее 22% белка                        от общего веса смеси

не более 5% клетчатки

Требуется определить количество (в кг) каждого из трех ингредиентов, образующих смесь минимальной стоимости, при соблюдении требований к общему расходу кормовой смеси и ее питательности.

 

Таблица 1.3

 

 

Математическая формулировка задачи.

Введем следующие обозначения:

Х₁ - содержание известняка в смеси (кг);

Х₂ - содержание зерна в смеси (кг);

Х₃ - содержание соевых бобов в смеси (кг);

Общий вес смеси, еженедельно расходуемый на кормление цыплят:

20 000 ´ 0.5 = 10 000 кг.

 

Ограничения, связанные с содержанием кальция, белка и клетчатки в кормовом рационе, имеют вид:

0.38Х₁ + 0.001Х₂ + 0.002Х₃  0.008 ´ 10 000,

0.09Х₂ +  0.50Х₃   0.22  ´ 10 000,

0.02Х₂ +  0.08Х₃   0.05  ´ 10 000.

 

Окончательный вид математической формулировки задачи:

при ограничениях

Х₁ + Х₂ + Х₃ = 10 000

0.38Х₁ + 0.001Х₂ + 0.002Х₃  80

0.09Х₂ +  0.50Х₃   2200                                      (1.3)

0.02Х₂ +  0.08Х₃   500

Х_j  0,   j = 1, 2, 3. 

Пример 1.4 (задача о раскрое или минимизации отходов (обрезков)). Продукция бумажной фирмы выпускается в виде бумажных рулонов стандартной ширины – по 2 метра. По специальным заказам потребителей фирма поставляет рулоны и других размеров, для чего производится разрезание стандартных рулонов. Типичные заказы на рулоны нестандартных размеров приведены в табл. 1.4.

 

                                                                           Таблица 1.4.

 

 

Требуется найти такие сочетания различных вариантов разрезания стандартных рулонов, чтобы поступившие заказы полностью удовлетворить с минимальными потерями (отходами). Рассмотрим все возможные варианты раскроя стандартного рулона, соответствующие данные сведем в табл. 1.5.

Определим переменные: Х_j – количество стандартных рулонов, разрезаемых по варианту j, j=1,2,…,6.

Ограничения непосредственно связаны с требованием обеспечить изготовление требуемого количества нестандартных рулонов.  Используя данные табл. 1.5, получим:

 

Таблица 1.5

 

 

2Х2+2Х3+4Х4+Х5=150 – количество рулонов шириной 0,5 м,

Х1+Х2+2Х5=200 – количество рулонов шириной 0,7м,

Х1+Х3+2Х6=300 – количество рулонов шириной 0,9м.

Выражение для суммарной величины потерь бумаги (отходы) (в м) имеет вид

0,4Х1+0,3Х2+0,1Х3+0,1Х5+0,2Х6

Таким образом, математическая модель в общем виде имеет вид

=0.4X₁+0.3X₂+0.1X₃+0.1X₅+0.2X₆

 

при ограничениях:

                   2X₂+2X₃+4X₄+X₅=150

                   X₁+X₂+2X₅=200                                                  

                   X₁+X₃+2X₆=300  

         ; X_j– целые;  j=1,...,6.

 

Домашнее задание №1

 

Составить математическую модель задачи.

1. Завод-производитель высокоточных элементов для автомоби­лей выпускает два различных типа деталей: Х и Y. Завод располагает фондом рабочего времени в 4000 чел .-ч. в неделю. Для производства одной детали типа Х требуется 1 чел.-ч, а для производства одной детали типа Y — 2 чел.-ч. Производ­ственные мощности завода позволяют выпускать максимум 2250 деталей типа Х и 1750 деталей типа Y в неделю. Каждая деталь типа Х требует 2 кг металлических стержней и 5 кг листового металла, а для производства одной детали типа Y необходимо 5 кг металлических стержней и 2 кг листового металла. Уровень запасов каждого вида металла составляет 10000 кг в неделю. Кроме того, еженедель­но завод поставляет 600 деталей типа Х своему постоянному заказчику. Существу­ет также профсоюзное соглашение, в соответствии с которым общее число произ­водимых в течение одной недели деталей должно составлять не менее 1500 штук.

Составить математическую модель задачи, если необходимо получить информацию, сколько деталей каждого типа следует производить, чтобы максимизировать общий доход за неделю при том, что доход от производства одной детали типа Х составляет 30 ф. ст., а от производства одной детали типа Y—40 ф. ст.?

 

2. Завод по производству электронного оборудования выпускает персональные компьютеры и системы подготовки текстов. В настоящее время освоены две модели:

а) "Юпитер" — объем памяти 1 Гб, одинарный дисковод;

б) "Марс"   — объем памяти 2 Гб,  двойной дисковод.

В производственный процесс вовлечены три цеха завода — цех узловой сборки, сборочный и испытательный. Распределение времени, требуемого для обработки каждой модели в каждом цехе, а также максимальные производственные мощности цехов приведены в табл.Отдел исследований рынка производит периодическую оценку потребительского спроса на каждую модель. Максимальные прогнозные значения спроса и доходы от реализации единицы продукции каждой модели также содержатся в табл.

Построить математическую модель для изложенной проблемы производства изделий в ассортименте, если цель состоит в максимизации общего ежемесячного дохода.

 

Время, требуемое на обработку каждой модели в каждом цехе

 

 

3. Менеджер по ценным бумагам намерен разместить 100000 ф. ст. капитала таким образом, чтобы получать максимальные годовые проценты с дохода. Его выбор ограничен двумя возможными объектами инвестиций: А и В. Объект А позволяет получать 6% годовых, объект В — 8% годовых. Для всех объектов степень риска и условия размещения капитала различны. Чтобы не подвергать риску имеющийся капитал, менеджер принял решение, что не менее половины инвестиций необходимо вложить в объект А. Чтобы обеспечить ликвидность, не менее 25% общей суммы капитала нужно поместить в объект В. Особенности налоговой политики требуют, чтобы в объект А было вложено не менее 30% капитала. Сформулируем для изложенной проблемы распределения инвестиций математическую модель.

 

4. "PrincetownPaintsLtd" выпускает два основных типа румян —перламутро­вые и матовые — с использованием одинаковых смесеобразующих машин и видов работ. Главному бухгалтеру фирмы было поручено разработать для компании план производства на неделю. Информация о ценах продаж и стоимости 100 л товара приведена в таблице (ф. ст.).

 

 

 

Стоимость 1 чел.-ч составляет 3 ф. ст. а стоимость 1 ч приготовления смеси — 4 ф. ст. Фонд рабочего времени ограничен 8000 чел.-ч. в неделю, а ограничение на фонд работы смесеобразующих машин равно 5900 ч в неделю.

В соответствии с контрактными соглашениями компания должна производить 25000 л матовых румян в неделю. Максимальный спрос на перламутровые румяна — 29000 л в неделю.

Требуется сформулировать математическую модель задачи, позволяющую определить объемы производства матовых и перламутровых румян в неделю, при которых достигается максимальное значение получаемой за неделю прибыли.

 

5. Администрация компании "NemesisCompany", осуществляя рационализаторскую программу корпорации, приняла решение о слиянии двух своих заводов в Аббатс-филде и Берчвуде. Предусматривается закрытие завода в Аббатсфилде и за счет этого — расширение производственных мощностей предприятия в Берчвуде. На настоящий момент распределение рабочих высокой и низкой квалификации, занятых на обоих заводах, является следующим:

 

 

В то же время после слияния завод в Берчвуде должен насчитывать 240 рабочих высокой и 320 рабочих низкой квалификации.

После проведения всесторонних переговоров с привлечением руководителей профсоюзов были выработаны следующие финансовые соглашения:

1. Все рабочие, которые попали под сокращение штатов, получат выходные пособия следующих размеров:

Квалифицированные рабочие       - 2000 ф. ст.;

Неквалифицированные рабочие    - 1500 ф. ст.

2. Рабочие завода в Аббатсфилде, которые должны будут переехать, получат пособие по переезду в размере 2000 ф. ст.

3. Во избежание каких-либо преимуществ для рабочих Берчвудского завода доля бывших рабочих завода в Аббатсфилде на новом предприятии должна совпа­дать с долей бывших рабочих Берчвудского завода.

Требуется построить модель линейного программирования, в которой определяется, как осуществить выбор работников нового предприятия из числа рабочих двух бывших заводов таким образом, чтобы минимизировать общие издержки, свя­занные с увольнением и переменой места жительства части рабочих.

 

6. Компания "BermudaPaint" — частная промышленная фирма, специализирующаяся на производстве технических лаков. Представленная ниже таблица содержит информацию о ценах продажи и соответствующих издержках производства единицы полировочного и матового лаков.

 

 

Для производства 1 галлона матового лака необходимо затратить 6 мин трудозатрат, а для производства одного галлона полировочного лака — 12 мин. Резерв фонда рабочего времени составляет 400 чел .-ч. в день. Размер ежедневного запаса необходимой химической смеси равен 100 унциям, тогда как ее расход на один галлон матового и полировочного лаков составляет 0,05 и 0,02 унции соответственно. Технологические возможности завода позволяют выпускать не более 3000 галлонов лака в день.

В соответствии с соглашением с основным оптовым покупателем компания должна поставлять ему 5000 галлонов матового лака и 2500 галлонов полировочного лака за каждую рабочую неделю (состоящую из 5 дней). Кроме того, существует профсоюзное соглашение, в котором оговаривается минимальный объем производства в день, равный 2000 галлонов. Администрации данной компании необходимо определить ежедневные объемы производства каждого вида лаков, которые позволяют получать максимальный общий доход.

Требуется:

а) Построить линейную модель для производственной проблемы, с которой столкнулась компания.

б) Используя графический метод, определить ежедневный оптимальный план производства и соответствующую ему величину дохода.

7. На мебельной фабрике из стандартных листов фанеры необ­ходимо вырезать заготовки трех видов в количествах, соответственно равных 24, 31 и 18 шт. Каждый лист фанеры может быть разрезан на заготовки двумя способами. Количество получаемых заготовок при данном способе раскроя приведено в таблице. В ней же указана величина отхо­дов, которые получаются при данном способе раскроя одного листа фанеры.

 

 

Определить, сколько листов фанеры и по какому способу следует раскроить так, чтобы было получено не меньше нужного количества заготовок при минимальных отходах.

 

8. В отделе технического контроля (ОТК) некоторой фирмы работают контролеры разрядов 1 и 2. Норма выработки ОТК за 8-часовой рабочий день составляет не менее 1800 изделий. Контролер разряда 1 проверяет 25 изделий в час, причем не ошибается в 98% случаев. Контролер разряда 2 проверяет 15 изделий в час; и его точность составляет 95%.

Заработная плата контролера разряда 1 равна 4 долл. в час, контролер разряда 2 получает 3 долл. в час. При каждой ошибке контролера фирма несет убыток в размере 2 долл. Фирма может использовать 8 контролеров разряда 1 и 10 контролеров разряда 2. Руководство фирмы хочет определить оптимальный состав ОТК, при котором общие затраты на контроль будут минимальными.

 

9. Фирма, специализирующаяся на производстве полуфабрикатов, выпускает три различных продукта, каждый из которых получается путем определенной обработки картофеля. Фирма может закупить картофель у двух различных поставщиков. При этом объемы продуктов 1, 2, 3, которые можно получить из одной тонны картофеля первого поставщика, отличаются от объемов, получаемых из того же количества картофеля второго поставщика. Соответствующие показатели приведены в таблице

 

 

Какое количество картофеля следует купить у каждого из поставщиков?

 

10.  Фирма, имеющая лесопильный завод и фабрику, на которой изготавливается фанера, столкнулась с проблемой наиболее рационального использования лесоматериалов. Чтобы получить 2.5 м³ комплектов пиломатериалов, необходимо израсходовать 2.5 куб. м еловых и 7.5 куб. м пихтовых лесоматериалов. Для приготовления 100 кв.м фанеры требуется 5 куб. м еловых и 10 куб. м пихтовых материалов. Фирма имеет 80 куб. м еловых и 180 куб. м пихтовых лесоматериалов.

Согласно условиям поставок, в течение планируемого периода необходимо произвести по крайней мере 10 куб. м пиломатериалов и 1200 кв. м фанеры. Доход с 1 куб. м пиломатериалов составляет 16 долл., а со 100 кв. м фанеры - 60 долл.

Определить оптимальные объемы производства пиломатериалов и фанеры.

 

ДОМАШНЕЕ ЗАДАНИЕ №2

 

Составить математическую модель задачи:

Из трех сортов бензина образуются две смеси. Первая состоит из А₁ % бензина первого сорта, В₁ % бензина 2-го сорта, С₁ % бензина 3-го сорта; вторая – А₂ % - 1-го, В₂ % - 2-го, С₂ % - 3-го сорта. Цена 1-ой смеси - 305 у.е., второй - 200 у.е. за тонну. Сколько смеси первого и второго вида можно изготовить из “а” тонн 1-го сорта, “в” тонн 2-го сорта и “с” тонн 3-го сорта, чтобы получить максимальный доход?

 

 

ДОМАШНЕЕ ЗАДАНИЕ №3

 

Составить математическую модель задачи.

1. Производитель элементов центрального отопления изготовливает радиаторы 4 моделей (A,B,C,D). Ограничения на производство обусловлены количеством рабочей силы и количеством стальных листов, из которых изготавливают радиаторы.

 

Кол-во стального листа- не более 2500 м², количество человеко-часов- не более 500. Решите задачу с максимезацией прибыли в качестве целевой функции.

 

2. Фирма производит три вида продукции (A, B, C), для выпуска каждого из них требуеться определенное время обработки на всех 4 устройствах I, II, III, IV.

 

 

Пусть время работы на устройствах соответственно 64, 32, 41 и 52 часа. Определите, какую продукцию и в каких количествах следует производить. Рынок сбыта каждого продукта неограничен. Рассмотреть задачу максимизации прибыли.

 

3. Прибыль от изделий A, B ,C составляет, соответственно, 13, 14, 15 единиц. Для каждого изделия требуеться время использования станка I и II, которые доступны, соответственно, 11 и 14 часов в день:

 

	A	B	C
I	2	3	3
II	4	1	2

 

Найдите оптимальный план производства.

 

4. Фирма, выпускающая трикотажные изделия, использует для производства продукции 2 вида сырья.

		Затраты	на единицу	продукции
Сырье	Запас сырья	свитер	палантин	пуловер
Чистая шерсть	160	0,4	0,2	0,8
Полиамид	60	0,2	0,1	0,2
Прибыль за изделие, ден. ед.		160	50	120

 

Найти план выпуска готовой продукции, максимизирующий прибыль.

 

5. В торговом зале необходимо выставить для продажи товары Т1 и Т2. Рабочее время продавцов не превышает 340 часов, а площадь торгового зала, которую можно занять не превышает 120 м². Каждая реализованная единица товара приносит прибыль, соответственно, в 50 и 80 ден. ед. Нормы затрат ресурсов на единицу проданного товара приведены в таблице:

 

Ресурсы	Т1	Т2
Рабочее время, ч	0,4	0,6
Площадь, м2	0,2	0,1

 

Найти оптимальную структуру товарооборота (чем меньше единиц товара, тем лучше), обеспечивающую прибыль не менее 30000 ден. ед.

 

6. Фирма занимается составление диеты, содержащей по крайней мере 20 единиц белков, 30 единиц углеводов, 10 единиц жиров и 40 единиц витаминов. Как дешевле всего достичь этого при указанных в таблице ценах на 1 кг( или 1л) имеющихся продуктов?

 

	Хлеб	Соя	Сушеная рыба	Фрукты	Молоко
Белки	2	12	10	1	2
Углеводы	12	0	0	4	3
Жиры	1	8	3	0	4
Витамины	2	2	4	6	2
Цена	12	36	32	18	10

 

7. Стандартом предусмотрено, что октановое число автомобильного бензина А-76 должно быть не ниже 76, а содержание серы- не более 0,3%. Для изготовления такого бензина на заводе используеться смесь четырех компонентов. Данные о ресурсах приведены в таблице:

 

Характеристика	Компонент	автомобильного	бензина
	№1	№2	№3	№4
Октановое число	68	72	80	90
Содержание серы,  %	0,35	0,35	0,3	0,2
Ресурсы, т	700	600	500	300
Себестоимость, ден. ед./ тонн	40	45	60	90

 

Требуется определить, сколько тонн каждого компонента следует использовать для получения 1000 т автомобильного бензина А- 76, чтобы его себестоимость была минимальной.

 

8. В пекарне для выпечки 4 видов хлеба используются мука двух сортов, маргарин и яйца. Имеющееся оборудование позволяет переработать в сутки не более 250 кг муки I сорта, 200 кг муки II сорта, 60 кг маргарина и 1380 штук яиц.

 

 

 

 

Определить суточный план выпечки хлеба, максимизирующий прибыль.

 

9. Прядильная фабрика для производства 2 видов пряжи использует три типа сырья- чистую шерсть, капрон и акрил.

Тип сырья	Нормы расхода	сырья на 1 т пряжи	Количество сырья
	Вид 1	Вид 2
Шерсть	0,5	0,2	600
Капрон	0,1	0,4	620
Акрил	0,4	0,2	500
Прибыль от реализации пряжи	1100	900

 

Требуется составить план производства пряжи с целью максимизации суммарной прибыли.

 

10. Чаеразвесочная фабрика выпускает чай сорта А и В, смешивая 3 ингредиента: индийский, грузинский и краснодарский чай.

Ингредиенты	Нормы	расхода (т/т)	Объем запасов (т)
Индийский чай	0,5	0,2	600
Грузинский чай	0,2	0,6	870
Краснодарский чай	0,3	0,2	430
Прибыль от реализации 1 т продукции	320	290

 

Требуется составить план производства чая, максимизирующий прибыль.

 

 

К оглавлению

Назад к разделу "ВВЕДЕНИЕ В ИССЛЕДОВАНИЕ ОПЕРАЦИЙ"

Вперед к разделу "2. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ"