6.2. Характеристический многочлен и характеристическое уравнение

 

Рассмотрим квадратную матрицу

 

 

 

Как было показано(6.1.), все матрицы, подобные матрице А, т.е. все матрицы вида А*= Т^-1АТ, где Т – любая невырожденная матрица (квадратная), обладают одним и тем же определителем |A|=|A*|.

Подобные матрицы обладают еще одной общей для всех них характеристикой.

Наряду с матрицей А рассмотрим матрицу

 

,

 

которая образована из А заменой диагональных элементов  элементами , где  - произвольное число. Определитель этой матрицы

 

представляет собой многочлен степени n относительно  (коэффициент при  равен (-1)ⁿ). Многочлен  называется характеристическим многочленом матрицы А.

Покажем, что все подобные матрицы имеют один и тот же характеристический многочлен, т.е. что , где А*=Т^-1АТ.

Для этого воспользуемся тождеством Е*= Т^-1ЕТ. Тогда, заменяя в матрице  матрицы А* и Е соответственно на Т^-1АТ и Т^-1ЕТ, получаем:

 

Таким образом, все подобные матрицы имеют один и тот же характеристический многочлен .

Алгебраическое уравнение n-й степени  называется характеристическим уравнением матрицы А, а его корни – характеристическими числами.

Характеристическое уравнение имеет вид

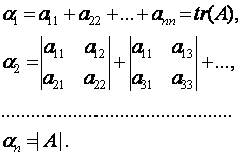
где – след k-го порядка матрицы А.

Следом k-го порядка  называется сумма возможных 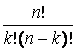 главных миноров k-ого порядка:

 

 

Характеристическое уравнение имеет n не обязательно различных корней . Каждому характеристическому корню соответствует собственный вектор с точностью до постоянного множителя.

Сумма характеристических корней равна следу матрицы А:

,

а произведение характеристических корней равно определителю матрицы А:

Число ненулевых корней совпадает с рангом матрицы линейного оператора.

Одним из методов для нахождения коэффициентов  характеристического уравнения является методом Фаддеева. Пусть линейный оператор  задан матрицей А. Тогда коэффициенты  вычисляются по следующей схеме:

 

 

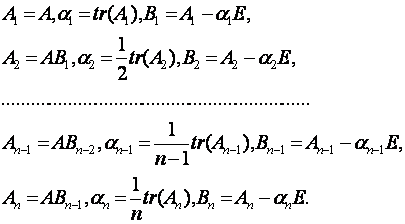
Пример. Найти собственные значения линейного оператора , заданного матрицей

.

 

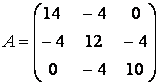Решение. Характеристическое уравнение имеет вид

где

 

 

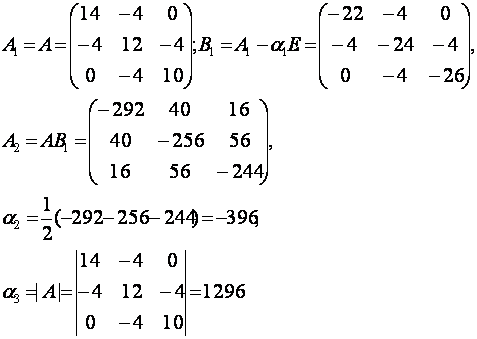
В итоге получаем следующее характеристическое уравнение:

или  откуда  - собственные значения линейного оператора .

 

Теорема Гамильтона-Кэли. Каждая квадратная матрица является корнем своего характеристического многочлена.

Доказательство. Рассмотрим многочлен

.

(6.2.1)

 

Пусть матрица В является присоединенной к матрице . Тогда имеем

.

(6.2.2)

 

Элементами матрицы В являются многочлены от  степени не выше (n-1). Поэтому матрицу В можно представить в следующем виде:

(6.2.3)

 

Подставляя выражения матрицы В из (6.2.3) и многочлена  из (6.2.1) в равенство (6.2.2), получим

или

(6.2.4)

Приравнивая коэффициенты при одинаковых степенях  в обеих частях равенства (6.2.4), получим

 

 

Умножим равенства (6.2.5) соответственно на  и сложим полученные результаты:

 

или

,

 

откуда следует, что . Теорема доказана.

 

Пример. Линейный оператор  задан матрицей

.

 

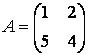Найти  и показать, что .

Решение. Составим матрицу

 

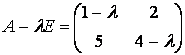
Многочлен  имеет вид

.

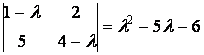Тогда

.

 

 

 

К оглавлению

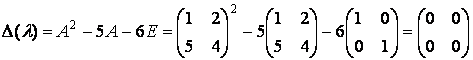Назад к разделу "ГЛАВА 6. ЛИНЕЙНЫЕ ОПЕРАТОРЫ"

Вперед к разделу "6.3. Собственный вектор и собственное число линейного оператора"