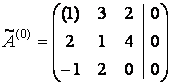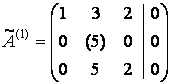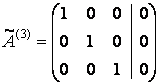5.5. Преобразование координат при изменении базиса

 

Пусть  и  - два базиса пространства R_n. Каждый вектор  можно выразить через векторы :

 

Выражения (5.5.1) показывают, что новые базисные векторы  получаются из старых базисных векторов  с помощью матрицы:

,

 

причем коэффициенты их разложений по старым базисным векторам образуют столбцы этой матрица.

Матрица А называется матрицей перехода от базиса  к базису . Определитель матрицы А отличен от нуля, так как в противном случае ее столбцы, а следовательно, и векторы  были бы линейно зависимы.

 

Рассмотрим, как связаны между собой координаты одного и того же вектора  в старом и новом базисах. Пусть

 

(5.5.2)

 

и в то же время

(5.5.3)

 

Подставим в (5.5.3) вместо  их выражения из (5.5.1):

(5.5.4)

 

Из (5.5.2) и  (5.5.4) в силу единственности разложения вектора  по базису  получаем

,

 

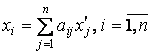или в матричном виде

X=AX',

(5.5.5)

где , .

Уравнение (5.5.5.) показывает связь между координатами  х_j и x'_j вектора  в базиcах  и , .

Из (5.5.5.) получаем:

X'=А^-1Х

Таким образом, при переходе от базиса  к базису  координаты вектора  преобразуются с помощью матрицы А^-1, являющейся обратной к транспонированной матрице, задающей преобразование базисов.

Пример. В базисе , ,  пространства R₃ заданы векторы , , , . Показать, что векторы  образует базис. Найти координаты вектора  в базисе . Выразить связь между базисами  и .

Решение. Векторы  образуют базис пространства R₃, если они линейно независимы. Векторы  линейно независимы если векторное равенство  выполняется тогда и только тогда, когда , , . Найдем решение векторного равенства

 

 

методом Жордана-Гаусса.

 

откуда .

Система векторов   линейно независима и, следовательно, образует базис в R₃.

Выразим каждый вектор  через векторы :

 

 

Матрица А перехода от базиса  к базису  имеет вид:

.

 

 

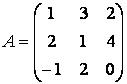Вычислив

,

 

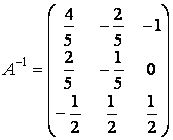определим координаты  вектора  в новом базисе

.

 

 

Таким образом, в базисе  вектор  определяется координатами .

Связь между базисом  и базисом  определяется из следующих соотношений:

 

,

 

,

 

,

 

или в матричном виде:

E=XA,

где

 

.

 

Решение данного матричного уравнения имеет вид X=A^-1, откуда получаем

,

,

,

 

Данные соотношения выражают связь между базисами.

 

 

К оглавлению

Назад к разделу "5.4. Изоморфизм векторных пространств"

Вперед к разделу "5.6. Евклидово пространство"