5.3. Базис векторного пространства

 

Определение. Совокупность n линейно независимых векторов  пространства R_n называется его базисом. Согласно определению n мерного векторного пространства R_n в нем существует n линейно независимых векторов, т.е. существует базис.

 

Теорема. Каждый вектор  векторного пространства можно представить, и притом единственным образом как линейную комбинацию векторов базиса.

Доказательство. Пусть, векторы  образуют базис в R_n. Присоединим к ним произвольный вектор  из R_n. Так как каждая система из (n+1) векторов пространства R_n линейно зависима, то линейно зависима и система , т.е. существуют такие не равные одновременно нулю числа

 что

(5.3.1)

При этом , так как иначе из формулы (5.3.1) следовала бы линейная зависимость векторов . Выражая из (5.3.1) вектор , получим

 

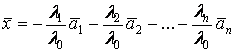
Полагая 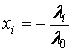, , будем иметь

Данное представление вектора  через векторы  единственно, так как если

 

  и , то

 

. Ввиду линейной независимости векторов , , откуда .

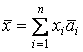Таким образом, если в n-мерном векторном пространстве R_n задан базис , то, используя выражение  можно установить взаимно однозначное соответствие между векторами этого пространства и упорядоченными последовательностями из n чисел . Числа  будем называть координатами вектора  в базисе  и будем писать . Из приведенной теоремы следует, что два вектора  и 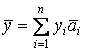 в R_n равны тогда и только тогда, когда их координаты в базисе  равны, т.е. когда .

 

Рассмотрим действия над векторами в координатной форме.

Пусть в пространстве R_n задан базис . Так как любой вектор из R_n можно представить, и притом единственным образом, в виде линейной комбинации базисных векторов, т.е.

 

,

 

то на основании аксиом, которым удовлетворяют операции сложения и умножения на число, имеем

 

,

.

 

Отсюда следует, что если векторы пространства R_n, заданы своими координатами относительно некоторого базиса , то при сложении векторов или умножении их на число  координаты векторов соответственно складываются или умножаются на . Таким образом,

,

 

и если

 

где

,

,

 

…………………….

 

,

,

то

,

,

 

………………………………..

.

 

 

У нулевого вектора  все координата равны нулю, так как из равенства  ввиду линейной независимости векторов , вытекает, что . Вектор, противоположный к  равен  так как .

 

Примеры.

I.                     Для случая трехмерного пространства R₃ определение координат вектора совпадает с имеющимся в аналитической геометрии определением координат вектора в некоторой системе координат.

II.                  Пусть R_n – пространство, векторами которого являются упорядоченные системы  из n чисел.

Очевидно, что n векторов

,

,

 

………………..

 

,

образуют базис этого пространства. Найдем координаты  вектора  в этом базисе:

 

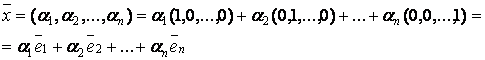
Отсюда следует, что числа  можно рассматривать как координаты вектора  в базисе  пространства .

III.  - пространство, векторами которого являются многочлены степени меньшей либо равной (). Простейшим базисом является совокупность векторов . Тогда координатами многочлена  в этом базисе являются его коэффициенты . Выберем другой базис: . Каждый многочлен по формуле Тейлора может быть представлен в виде 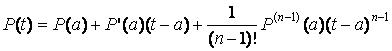. Таким образом, в этом базисе P(t) имеет координаты .

 

 

К оглавлению

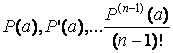Назад к разделу "5.2. Линейная зависимость и независимость векторов"

Вперед к разделу "5.4. Изоморфизм векторных пространств"