2.3. Миноры и алгебраические дополнения
Вычисление определителей на основании данного выше определения представляет некоторые трудности. Существует более простой метод вычисления определителей, основанный на том, что определитель порядка n может быть выражен через определители более низких порядков.
Пусть дана квадратная матрица ![]() .
Будем называть минором элемента
.
Будем называть минором элемента ![]() матрицы А
определитель (n-1)-го порядка, соответствующий
матрице, которая получается из матрицы А вычеркиванием i–ой строки и j–го
столбца. Минор элемента
матрицы А
определитель (n-1)-го порядка, соответствующий
матрице, которая получается из матрицы А вычеркиванием i–ой строки и j–го
столбца. Минор элемента ![]() будем
обозначать символом M
будем
обозначать символом M![]() .
.
Например, 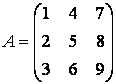 ,
, 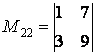 .
.
Алгебраическим дополнением A![]() элемента
элемента ![]() матрицы А
называется его минор, взятый со знаком (-1)
матрицы А
называется его минор, взятый со знаком (-1)![]() ,
т.е.
,
т.е. ![]() .
Например, в предыдущей матрице
.
Например, в предыдущей матрице 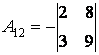 .
.
Теорема.
Произведение любого элемента ![]() на его
алгебраическое дополнение в определителе |A| является алгебраической суммой, слагаемые которой
будут некоторыми членами определителя |A|, причем их знаки в этой сумме совпадают с теми
знаками, с которыми они входят в состав определителя.
на его
алгебраическое дополнение в определителе |A| является алгебраической суммой, слагаемые которой
будут некоторыми членами определителя |A|, причем их знаки в этой сумме совпадают с теми
знаками, с которыми они входят в состав определителя.
Покажем сначала, что произведение ![]() является алгебраической суммой, слагаемые
которой удовлетворяют условию теоремы.
является алгебраической суммой, слагаемые
которой удовлетворяют условию теоремы.
В определителе

М![]() занимает правый нижний угол. Число i+j
является в этом случае четным и поэтому
занимает правый нижний угол. Число i+j
является в этом случае четным и поэтому ![]() .
.
Произвольный член
|
|
(2.3.1) |
![]() имеет в миноре
имеет в миноре ![]() знак
знак ![]() ,
где inv(
,
где inv(![]() ,
,![]() ,...,
,...,![]() )
есть число инверсий в подстановке
)
есть число инверсий в подстановке 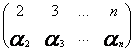 .
.
Умножая ![]() на (2.3.1), получим произведение
на (2.3.1), получим произведение
|
|
(2.3.2) |
элементов, расположенных в разных строках и разных
столбцах определителя |A|. Поэтому каждое такое произведение (2.3.2) будет
членом определителя |A|. Знаки членов (2.3.2) и (2.3.1) совпадают, так как знак
члена (2.3.2) определяется выражением ![]()
![]() =
=![]() .
Такой же знак имеет каждый член (2.2.3) и в определителе |A|, так как четность подстановки
.
Такой же знак имеет каждый член (2.2.3) и в определителе |A|, так как четность подстановки 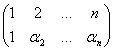 ,
,
составленной из индексов этого члена, определяется
выражением ![]() .
.
Перейдем к рассмотрению общего случая.
Переставляя соседние строки и столбцы определителя |A|, передвинем произвольный элемент ![]() в левый верхний
угол. Для этой цели переставим i–ую строку на (i–1) раз и j–ый столбец на (j–1) раз. Очевидно, что при данной
перестановке взаимное расположение строк и столбцов в миноре M
в левый верхний
угол. Для этой цели переставим i–ую строку на (i–1) раз и j–ый столбец на (j–1) раз. Очевидно, что при данной
перестановке взаимное расположение строк и столбцов в миноре M![]() остается без
изменения. После этих преобразований получим новый определитель |A
остается без
изменения. После этих преобразований получим новый определитель |A![]() | с тем же минором M
| с тем же минором M![]() для элемента
для элемента ![]() , но расположенный в правом нижнем углу определителя |A
, но расположенный в правом нижнем углу определителя |A![]() |.
|.
Как доказано выше, произведение ![]() M
M![]() является суммой
некоторого числа членов определителя |A
является суммой
некоторого числа членов определителя |A![]() |. Однако определитель |A
|. Однако определитель |A![]() | получен из определителя |A| путем (i+j-2) перестановок строк и столбцов, и поэтому
члены определителя |A
| получен из определителя |A| путем (i+j-2) перестановок строк и столбцов, и поэтому
члены определителя |A![]() | отличаются от соответствующих членов определителя |A| лишь знаком
| отличаются от соответствующих членов определителя |A| лишь знаком ![]() .
Отсюда следует, что произведение
.
Отсюда следует, что произведение ![]() состоит из некоторого количества членов
определителя |A|, взятых с такими же знаками, какие они имеют в этом
определителе. Теорема доказана.
состоит из некоторого количества членов
определителя |A|, взятых с такими же знаками, какие они имеют в этом
определителе. Теорема доказана.
Назад к разделу "2.2. Определители и их свойства"
Вперед к разделу "2.4. Вычисление определителей n-го порядка"