Handbook по дисциплине
«Математическое моделирование»
Программа магистерской подготовки

Кафедра Информационных систем и технологий
Прокимнов Н.Н.
Handbook по дисциплине
«Математическое моделирование»
Программа магистерской подготовки
Тема 1. Основные концепции моделирования
Вопрос 1. Основы методологии моделирования.
Вопрос 2. Классификация моделей.
Вопрос 3. Требования, предъявляемые к моделям.
Тема 2. Построение математических моделей
Вопрос 1. Теоретические основы математического моделирования.
Тема 3. Пуассоновский поток и проверка статистических гипотез
Вопрос 1. Постановка задачи проверки гипотез.
Вопрос 2. Пуассоновский поток.
Вопрос 3. Пример проверки гипотез.
Тема 4. Моделирование марковских процессов
Вопрос 1. Понятие марковского процесса.
Вопрос 2. Классификация марковских процессов.
Вопрос 3. Граф состояний и переходов.
Вопрос 4. Марковский процесс с дискретными состояниями и дискретным временем.
Вопрос 5. Предельные вероятности цепи Маркова.
Тема 5. Непрерывные марковские процессы
Вопрос 1. Описание непрерывных цепей Маркова.
Вопрос 2. Уравнения Колмогорова.
Вопрос 3. Процессы гибели и размножения.
Тема 6. Модели систем массового обслуживания
Вопрос 1. Система массового обслуживания.
Вопрос 2. Моделирование одноканальной СМО с отказами.
Вопрос 3. Оптимизация показателей многоканальной СМО с отказами.
Вопрос 4. Обслуживание с очередями.
Вопрос 5. Многоканальная СМО сограниченной очередью.
Тема 7. Модели на основе метода статистических испытаний
Вопрос 1. Метод статистических испытаний.
Вопрос 2. Случайные и псевдослучайные числа.
Вопрос 3. Имитация случайных событий.
Вопрос 4. Пример применения метода Монте-Карло.
Тема 8. Основы имитационного моделирования
Вопрос 1. Концепции имитационного моделирования.
Вопрос 2. Имитация случайных величин с заданными законами распределения.
Вопрос 3. Обработка результатов запусков программной модели.
Тема 9. Моделирующие комплексы
Вопрос 1. Создание имитационных моделей с помощью систем моделирования.
Вопрос 2. Конструкционные элементы модели системы Pilgrim.
Вопрос 3. Средства описания модели в системе Pilgrim.
Тема 10. Программная модель в системе Pilgrim
Вопрос 1. Структура программной модели в системе Pilgrim.
Вопрос 3. Текст программной модели СМО.
Вопрос 4. Сборка и запуск исполнительного модуля модели.
Вопрос 5. Результаты моделирования.
Тема 11. CASE-системы в имитационном моделировании
Вопрос 1. Создание многослойных моделей.
Вопрос 2. Использование узла parent.
Вопрос 3. Использование узлов pay, rent, down.
Вопрос 4. Многослойная модель бизнес-процесса.
Тема 12. Средства и приемы создания имитационных моделей
Вопрос 1. Моделирование замкнутых систем.
Вопрос 2. Определение нестандартных выходных параметров.
Вопрос 4. Построение гистограмм.
Тема 13. Планирование модельных экспериментов
Вопрос 1. Основы теории планирования эксперимента.
Вопрос 2. Отсеивающий эксперимент.
Вопрос 3. Аналитическое описание функции отклика.
Вопрос 4. Поиск оптимальных значений.
Дисциплина посвящена изучению основных принципов, методов и практических правил математического моделирования, проведения анализа, научных исследований и принятия практических рациональных решений применительно к направлению подготовки магистров 230700 – «Прикладная информатика»:
· исследование и оптимизация свойств локальных информационных систем;
· исследование и оптимизация свойств информационных и образовательных сетей;
· исследование и оптимизация свойств систем со сложной (многослойной) функциональной структурой.
Дисциплина формирует общую систему теоретических и концептуальных представлений о методологических основах проведения научных исследований, позволяет освоить ряд практических навыков и умений по применению полученных знаний для решения прикладных задач в своей области деятельности и написанию магистерской диссертации.
Содержание (контент) дисциплины содержит, в первую очередь, те разделы области математическое моделирование, которые наиболее важны магистрам, специализирующимся в области систем информатизации и коммуникаций в вузах инженерно-экономической направленности.
Цели и задачи освоения дисциплины.
Целью дисциплины является изучение математического моделирования сложных систем информационных систем, а также современных наукоёмких компьютерных технологий, используемых как средства моделирования, анализа и оценки систем и проектов, в том числе в условиях неопределённости и рисков.
По завершении освоения данной дисциплины студент должен обладать компетенциями:
общекультурными:
· способен совершенствовать и развивать свой интеллектуальный и общекультурный уровень, самостоятельно обучаться новым методам исследований (ОК-1);
· способен управлять знаниями в условиях формирования и развития информационного общества: анализировать, синтезировать, критически резюмировать и представлять информацию (ОК-6);
общепрофессиональными:
· способен на практике применять новые научные принципы и методы исследований (ПК-3);
научно-исследовательская деятельность:
· способен формализовать задачи в прикладной области, при решении которых возникает необходимость использования количественных и качественных оценок (ПК-6);
· способен ставить и решать прикладные задачи в условиях неопределенности и определять методы и средства их эффективного решения (ПК-7);
· способен проводить научные эксперименты, оценивать результаты исследований (ПК-8);
аналитическая деятельность:
· способен анализировать данные и оценивать требуемые знания для решения нестандартных задач с использованием математических методов и методов компьютерного моделирования (ПК-12);
· способен анализировать и оптимизировать прикладные и информационные процессы (ПК-14);
проектная деятельность:
· способен принимать эффективные проектные решения в условиях неопределенности и риска (ПК-18).
· научить проводить математическое моделирование сложных систем для их анализа и синтеза;
· научить построению математических моделей систем для получения их динамических характеристик;
· научить проводить оценку качества функционирования сложной динамической системы с помощью математической модели;
· научить современным подходам к компьютерному моделированию систем.
В результате изучения дисциплины студенты должны:
знать:
· возможности методологии и основные области ее применения, классификацию моделей и постановку основных задач, решение которых достигается наиболее эффективно с помощью применения математических моделей;
уметь:
· правильно анализировать проблемную ситуацию и формулировать задачи анализа и синтеза систем с ориентацией на применение для решения задач аппарата математического моделирования, рационально планировать экспериментальную работу с моделью, интерпретировать и анализировать результаты моделирования процессов и систем;
иметь представление:
· об особенностях и возможностях основных разновидностей математических моделей, типовых приемах, применяемых для построения моделей и получения необходимых результатов моделирования.
Вопросы отражают тематику разделов тематического плана программы курса «Математическое моделирование» Московского финансово-промышленного универститета «Синергия».
Результаты освоения дисциплины.
В результате освоения учебной дисциплины обучающиеся должны демонстрировать следующие квалификационные навыки:
· динамические оптимизационные модели;
· математические модели управления для оптимизации непрерывных и дискретных процессов, их сравнительный анализ;
· методы и средства создания математических моделей динамических объектов;
· современные подходы к компьютерному моделированию систем.
Уметь:
· осуществлять методологическое обоснование научного исследования;
· выбирать инструментарий для каждого этапа принятия решения; использовать инструментарий мониторинга исполнения решений;
· выбирать методы управления рисками;
· анализировать данные и оценивать требуемые знания для решения нестандартных задач с использованием математических методов и методов компьютерного моделирования.
Владеть:
· методами оптимизации прикладных и информационных процессов;
· методами улучшения параметров исследуемых систем, используя результаты моделирования.
· познакомиться с возможностями и аппаратом моделирования для решения задач анализа и проектирования сложных систем.
· понять особенности методологии;
· понять главные преимущества моделирования;
· более детально познакомиться с математическими моделями.
получите представление о:
· сущности моделирования и классификациях моделей;
· в каких областях наиболее широко используется моделирование;
будете знать:
· какие требования предъявляются к моделям;
· что означает адекватность модели и как она устанавливается;
· из каких шагов состоит процесс моделирования.
1. Основы методологии моделирования.
2. Классификация моделей.
3. Требования, предъявляемые к моделям.
Целью исследования обычно являются либо изучение механизма поведения объекта или явления, либо определение значений параметров исследуемого объекта, удовлетворяющих определенному критерию. Это означает, что в процессе исследования необходимо изменять значения параметров исследуемого объекта и таким образом измерять значения показателя, служащего аргументом критерия. Процесс исследования заканчивается, когда исследователь находит совокупность значений параметров объекта, удовлетворяющую заданному критерию с заданной достоверностью.
Проведение таких исследований называется экспериментом. На практике экспериментирование с реальными объектами, как правило, либо обходится очень дорого, либо вообще невозможно из-за нежелательных последствий эксперимента. Примерами таких задач могут быть задачи изучения социальных и экономических последствий от введения новых законодательных актов, исследование влияния, которое окажет на показатели безопасности воздушного движения оснащение воздушных судов новой системой предупреждения столкновений, или исследование характеристик устойчивости конструкции зданий (сооружений) для сейсмически опасного района.
Поэтому обычно в таких случаях для проведения научных экспериментов реальные объекты заменяются соответствующими им более простыми, безопасными и доступными объектами, свойства которых подобны свойствам исследуемых реальных объектов в своей существенной части. Методологической основой такого подхода является моделирование систем.
Моделирование представляет собой универсальный метод получения, описания и использования знаний и используется в любой профессиональной деятельности. В современной жизни, характеризующейся большим разнообразием и сильной взаимозависимостью явлений и процессов, роль и значение моделирования еще более усиливаются. Моделирование реальных систем живой и неживой природы позволяет исследователю или проектировщику выявлять связи между формальными знаниями и изучаемыми системами или процессами.
Методология моделирования применяется во многих областях человеческой деятельности. Из основных областей применения назовем такие области, как:
· построение теории исследуемой системы;
· управление системой в целом или отдельными ее подсистемами, выработка управленческих решений и стратегий;
· автоматизация системы или отдельных ее подсистем;
· обучение, как в прикладных областях знаний, так и в профессинальной сфере;
· прогнозирование реакции систем (выходных данных) на воздействия, ситуаций, состояний.
Модели и моделирование объединяют специалистов различных областей, работающих над решением междисциплинарных проблем, независимо от того, где эта модель и результаты моделирования будут применены. Вид модели и методы ее исследования больше зависят от информационно-логических связей элементов и подсистем моделируемой системы, ресурсов, связей с окружением, используемых при моделировании, а не от конкретной природы, конкретного наполнения системы.
Модели, в особенности модели математические, обладают и другой важной особенностью, а именно, позволяют развивать у исследователя модельный стиль мышления, что дает возможность вникать в структуру и внутреннюю логику моделируемой системы.
Чтобы получить представление об основной сущности понятия модель будем использовать такое ее определение:
Объект А есть модель объекта В, если:
1) А и В не идентичны друг другу;
2) А отвечает на вопросы относительно В.
Иначе говоря, модель представляет собой некоторый объект, замещающий объект-оригинал в целях его изучения или воспроизведения каких-либо его свойств, и есть, таким образом, результат отображения первого на второй.
Например, отображая объект-оригинал, представляющий собой физическую систему, на математическое описание в виде системы дифференциальных уравнений, получим математическую модель объекта-оригинала.
Построение модели есть системная задача, требующая анализа и синтеза исходных данных, гипотез, теорий, знаний специалистов. Системный подход позволяет не только построить модель реальной системы, но и использовать эту модель для оценки различных системных показателей, например, эффективности управления каким-либо объектом или качественных и количественных показателей деловых процессов, протекающих в некоторой структуре.
Любая модель строится и исследуется при определенных допущениях (гипотезах). Например, физическая система, состоящая из тела массы m, движущегося с ускорением a и находящегося под воздействием силы F, описывается математически уравнением F=ma и представляет собой математическую модель физической системы (второй закон Ньютона). Эта модель построена при таких допущениях относительно объекта-оригинала как:
1) трение отсутствует;
2) сопротивление воздуха ничтожно мало;
3) масса тела не меняется;
4) движение происходит с постоянным ускорением.
Когда же нам необходимо иметь инструмент для более точного количественного описания происходящих явлений (иными словами, получить более адекватную модель), мы будем вынуждены включить в рассмотрение какие-то из тех факторов, которыми до этого пренебрегали.
Под моделированием будем понимать процесс, в результате которого решаются две задачи:
1) создание модели для проведения исследований;
2) проведение на основе созданной модели экспериментов, необходимых для достижения конечной цели исследований.
Важно отметить то обстоятельство, что модель, появляющаяся как итог решения первого этапа моделирования, предназначена для решения с ее помощью конкретной задачи, которая должна формулироваться до начала работ по моделированию, и модель должна, следовательно, создаваться на основе гипотез, вытекающих из специфики и требований конечной цели исследований.
В широком смысле моделирование представляет собой научную дисциплину, в которой изучаются методы построения и использования моделей для познания реального мира.
Классификацию моделей на верхнем уровне (Рис. 1
Рис.) можно провести, выделив два основных класса – моделей натурных и моделей математических.

Рис. 1. Классификация моделей
При натурном моделировании используется либо сама исследуемая система, либо подобная ей. Модели в этих случаях представляют собой материальные объекты. Поэтому они иногда называются материальными моделями.
При исследовании сложных систем, как правило, создать адекватную физическую модель не представляется возможным. В этих случаях ограничиваются созданием и исследованием математических описаний закономерных отношений между значениями параметров оригиналов. Такие описания называются математическими моделями. Математическая модель - это образ исследуемого объекта, умозрительно создаваемый исследователем с помощью определенных формальных (математических) систем с целью изучения или оценивания определенных свойств данного объекта.
Математическое моделирование можно определить как процесс установления соответствия реальной системе математической модели и проведения исследований на этой модели, позволяющий получить характеристики реальной системы.
Применение математического моделирования дает возможность исследовать объекты, реальные эксперименты над которыми затруднены или невозможны в силу связанных с проведением экспериментов больших затрат, опасности для жизни или здоровья. Такие случаи возможны при изучении новой конструкции летательного аппарата, наличия физических (например, большая удаленность объекта от исследователя) или временных (проведение натурных экспериментов невозможно в установленные сроки) ограничений и т.п.
Одним из основных достоинств математического моделирования является их экономичность. По разным оценкам построение и применение математических моделей требует примерно в 10-100 раз меньших затрат по сравнению с затратами на физическое моделирование.
В зависимости от способов, которые используются для математического описания моделируемой системы и нахождения решения с помощью этого описания, различают аналитическое и компьютерное моделирование.
При аналитическом моделировании процессы функционирования элементов описываются в виде математических соотношений (алгебраических, интегральных, дифференциальных, логических и т.д.).
При компьютерном моделировании описание модели составляется либо в виде алгоритма (программы ЭВМ), либо в форме, которая может восприниматься (интерпретироваться) ЭВМ с целью проведения экспериментов. В зависимости от способа, который используется для решения математической модели, различают численное, статистическое и имитационное моделирование.
При численном моделировании для проведения расчетов используются методы вычислительной математики. От аналитического моделирования численное моделирование отличается тем, что возможно задание различных параметров модели.
Статистическое моделирование, или метод Монте-Карло состоит в обработке данных о системе (модели) с целью получения статистических характеристик системы. Его можно считать разновидностью имитационного моделирования, способ исследования процессов поведения вероятностных систем в условиях, когда неизвестны внутренние взаимодействия в этих системах. Он заключается в машинной имитации изучаемого процесса, который как бы копируется на вычислительной машине со всеми сопровождающими его случайностями; используется главным образом при решении задач исследования операций, в анализе производственной деятельности.
Когда внутренние взаимодействия между элементами системы и механизмы протекания процессов исследуемого объекта достаточно хорошо изучены и описаны, то становится возможным непосредственное воспроизведение протекающих процессов с помощью компьютерной программы. Такой подход называют имитационным моделированием, которое позволяет исследователю или аналитику добиться высокой точности результата при относительно невысоких затратах на его получение.
Математические модели, которые являются основным классом моделей изучаемых в настоящем курсе, можно классифицировать и по целому ряду специфических для них признаков. Укажем некоторые из основных классификаций математических моделей.
В зависимости от применяемого аппарата модель может быть отнесена к одному из следующих видов.
Функциональная – состоит из совокупности нескольких функций, описывающих взаимосвязи между различными параметрами моделируемой системы. Примером функциональной модели может быть выраженная вторым законом Ньютона зависимость между массой, силой и ускорением движущегося тела.
Логическая – состоит из логических высказываний (предикатов) относительно моделируемой системы. Например, правила выполнения арифметических действий над двоичными числами в процессоре ЭВМ могут быть описаны с помощью основных логических операций И, ИЛИ, НЕ.
Табличная – описывает структуру и/или поведение моделируемой системы в виде одной или нескольких таблиц. Так, эффективность применения того или иного антивирусного средства можно описать в виде таблицы, строками которой будут применяемые программы, а столбцами – виды вирусных атак.
Графовая – использует математическое понятие графа для представления моделируемых структур и взаимодействий между отдельными элементами структур. Например, с помощью графовой модели можно представить транспортную сеть с целью оптимизации ее структуры или нахождения оптимальных путей передвижения по этой сети (задача коммивояжера и т.п.).
Алгоритмическая – строится как формализованное описание логической последовательности действий, которые необходимо предпринять для достижения требуемой цели в моделируемой системе. Например, для нахождения критического пути в сетевом графе работ используется алгоритм (метод) критического пути, построенный на рекуррентном правиле.
Игровая – описывает поведение системы из нескольких субъектов (групп субъектов) с конфликтом или антагонизмом целей. Формализация осуществляется на основе аппарата теории игр.
Приведенный перечень не является исчерпывающим и отражает лишь наиболее распространенные типы моделей.
Назначение модели.
Если описание модели не содержит временного параметра, то модель называется статической. Примерами статических моделей являются планетарная модель атома и модель ДНК.
Если описание модели включает временной параметр, то модель называется динамической. Примером динамической модели может быть модель для определения величины пройденного пути свободно падающим телом, которая находится из выражения:
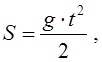
где
g – ускорение свободного падения;
t - время, прошедшее с момента начала движения.
Модель называется моделью с дискретным временем (или просто дискретной), если поведение моделируемой системы описывается только для дискретного набора моментов времени. Например, если рассматривать систему ведения артиллерийского огня, то решение задачи оценивания эффективности стрельбы можно проводить, привязываясь только к определенным временным моментам, а именно, к моментам произведения выстрела.
Модель называется моделью с непрерывным временем (или просто непрерывной), если поведение моделируемой системы описывается для любого момента времени ее функционирования. Например, в ранее приведенном примере свободно падающего тела величину пройденного пути модель позволяет определять в произвольные моменты времени.
Деление систем на непрерывные и дискретные довольно условно и определяется характером решаемой задачи.
По этому признаку принято подразделять модели на две большие группы – линейные и нелинейные.
В линейных моделях математическая связь ее выходных параметров с входными представляется с помощью линейных зависимостей.
В качестве примера можно еще раз использовать второй закон Ньютона, который выражается математически, как хорошо известно, следующим образом:
F=ma.
Другим примером может служить также хорошо известный закон Ома, устанавливающий связь меду величиной напряжения, силой тока и сопротивлением:
U = IR.
Однако довольно часто поведение исследуемой системы не подчиняется линейным зависимостям и для их описания нужно применять функции более сложного вида (степенные, логарифмические, показательные), что приводит к нелинейным моделям.
Построение и использование нелинейных моделей сопряжено со значительными трудностями, поэтому на практике чаще прибегают к кусочно-линейной аппроксимации (линеаризации) нелинейных моделей в целях упрощения задачи.
Определенность поведения.
Различают детерминированные и стохастические в зависимости от возможности или невозможности предсказать их поведение.
В детерминированной модели в каждый момент времени можно основываясь на значениях входных параметров, однозначно предсказать значения выходных параметров. К таким моделям можно отнести многие модели, применяемые в астрономии.
В стохастической (недетерминированной, вероятностной) модели в силу действия недостаточной изученных или вовсе неизвестных случайных факторов предсказать поведение модели однозначно нельзя. Описание и исследование моделируемой системы может быть построено на использовании аппарата теории вероятностей и математической статистики, а также известных законов распределения случайных величин. К стохастическим моделям можно отнести модели систем массового обслуживания (парикмахерская, банк, билетная касса, справочное бюро и т.п.), где момент прихода очередного требования и продолжительность нахождения его в системе однозначно непредсказуемы.
Чтобы соответствовать своему назначению и быть практически полезными модели должны отвечать ряду требований, вытекающих из сущности методологии и определяемых условиями конкретной задачи. Укажем основные из них, которые носят принципиальный и универсальный характер.
Создать модель в точности отображающую все свойства моделируемого объекта невозможно. Модель всегда отображает только некоторые аспекты системы, выбираемые исследователем для включения в модель в зависимости от того, насколько эти аспекты существенны с точки зрения решения основной задачи. Выбор цели, таким образом, определяет характер всей последующей работы, связанной с построением и использованием модели, а также полезность и надежность получаемого результата. Таким образом, основным и обязательным свойством модели является ее целенаправленность.
Свойство адекватности модели определяет ее пригодность в качестве инструмента проведения исследований и является основным ее свойством. Модель считается адекватной, если она отражает заданные свойства моделируемого объекта с приемлемой точностью. Точность определяется как степень близости значений выходных параметров модели к выходным параметрам объекта. Если в процессе построения модели допущены принципиальные ошибки, то говорить о ее точности не имеет смысла.
Реальный объект (Рис. 2а).

Рис. 2. Объект-оригинал (а) и его модель (б)
может быть описан функциональной
зависимостью между показателями его свойств Y и
множествами учтенных ![]() и неучтенных
и неучтенных
![]() факторов и параметров
факторов и параметров ![]() (определение этих терминов будет дано в
следующей теме):
(определение этих терминов будет дано в
следующей теме):
Однако в модели (
Рис.Рис. 2б) отображаются только те факторы и параметры объекта-оригинала, которые имеют существенное значение для решения поставленной задачи. Кроме того, измерения существенных факторов и параметров практически всегда содержат ошибки, обусловленные погрешностью измерительных приборов и незнанием некоторых факторов. В силу этого модель включает в себя только приближенное описание свойств изучаемого объекта, а математическая модель представляет собой еще и абстракцию изучаемого объекта.
Модели обычно отличаются от
своих оригиналов природой внутренних параметров. Подобие заключается в адекватности
реакции Y’ модели реакции Y оригинала на изменение внешних
факторов ![]() . Поэтому в общем случае
математическая модель представляет собой функцию:
. Поэтому в общем случае
математическая модель представляет собой функцию:
где
![]() внутренние
параметры модели, адекватные параметрам оригинала.
внутренние
параметры модели, адекватные параметрам оригинала.
Главным вопросом
математического моделирования является вопрос о том, насколько точно
составленная математическая модель отражает отношения между учитываемыми
факторами, параметрами и выходом (показателем оцениваемого свойства) Y реального
объекта, т.е., в какой степени уравнение ![]() (2) соответствует
уравнению
(2) соответствует
уравнению ![]() . (1).
. (1).
Иногда ![]() (2) можно получить в явном виде, например, в виде системы
дифференциальных уравнений или иных математических соотношений. Однако в более
сложных случаях вид уравнения
(2) можно получить в явном виде, например, в виде системы
дифференциальных уравнений или иных математических соотношений. Однако в более
сложных случаях вид уравнения ![]() (2) неизвестен и задача исследователя состоит, прежде
всего, в том, чтобы найти вид этого уравнения. При этом к числу
варьируемых параметров
(2) неизвестен и задача исследователя состоит, прежде
всего, в том, чтобы найти вид этого уравнения. При этом к числу
варьируемых параметров ![]() , относят все учитываемые
внешние факторы и параметры исследуемого объекта, а к числу искомых параметров
относят внутренние параметры модели
, относят все учитываемые
внешние факторы и параметры исследуемого объекта, а к числу искомых параметров
относят внутренние параметры модели ![]() , связывающие
факторы
, связывающие
факторы ![]() с показателем Y' наиболее
правдоподобным отношением. Решением этой проблемы занимается теория
планирования эксперимента, элементы которой рассматриваются в последней
теме настоящего курса. Положения этой теории применительно к указанной задаче позволяют,
основываясь на выборочных измерениях значений параметров
с показателем Y' наиболее
правдоподобным отношением. Решением этой проблемы занимается теория
планирования эксперимента, элементы которой рассматриваются в последней
теме настоящего курса. Положения этой теории применительно к указанной задаче позволяют,
основываясь на выборочных измерениях значений параметров ![]() и показателя Y', найти параметры
и показателя Y', найти параметры ![]() , при которых функция
, при которых функция ![]() (2) наиболее точно отражает реальную закономерность
(2) наиболее точно отражает реальную закономерность ![]() . (1).
. (1).
Точность модели различна в разных условиях функционирования объекта, которые характеризуются внешними параметрами. В пространстве внешних параметров необходимо выделить область адекватности модели, где погрешность меньше заданной предельно допустимой погрешности. Определение области адекватности моделей является довольно сложной и трудоемкой задачей, решение требующей больших вычислительных и временных ресурсов, которые с увеличением размерности пространства внешних параметров растут нелинейно. Эта задача по объему может значительно превосходить задачу параметрической оптимизации самой модели, поэтому для вновь проектируемых объектов может не решаться.
Универсальность модели определяется в основном числом и составом учитываемых в модели внешних и выходных параметров. Задачей разработчика модели является определение множества этих параметров таким образои, чтобы обеспечить получение нужных результатов в достаточно широкой области исследований.
Экономичность модели характеризуется затратами вычислительных ресурсов для ее реализации - затратами машинного времени и памяти. Для решения достаточно сложных задач это обстоятельство может иметь очень большое значение.
Противоречивость требований к модели - широкая область адекватности, высокая степень универсальности и экономичность - обусловливает необходимость создания для объектов одного и того же типа не одной модели, а некоторого их набора, в котором каждая модель предназначена для решения конкретных, в общем случае непересекающихся, задач.
Степень соответствия модели своему назначению и ее практическая полезность характеризуется также наличием у нее таких свойств как:
· Наглядность, под которой понимается обозримость основных свойств и отношений.
· Управляемость, предполагающая наличие в модели хотя бы одного параметра, изменениями которого можно имитировать поведение моделируемой системы в различных условиях.
· Доступность и технологичность для проведения исследования или воспроизведения поведения.
· Адаптивность, под которой понимается способность модели приспосабливаться к различным входным параметрам и воздействиям окружения.
· Способность к эволюции, т.е., к количественному и качественному развитию.
1. Решение многих научных и практических задач сопряжено с большими трудностями в силу невозможности проведения эксперимента с реальным объектом или связанных с проведением эксперимента большими затратами. Преодолеть эти трудности можно путем моделирования изучаемого объекта.
2. Методология моделирования является универсальной как по отношению к типу изучаемых объектов и явлений, так и в смысле постановок задач исследований, которые могут выходить за границы применимости классических теорий и требовать междисциплинарного подхода.
3. Для правильного выбора подхода к решению задач моделирования, так же как и в других областях науки необходима классификация моделей по различным признакам. Одним из наиболее распространенных классов моделей являются математические модели, дающие возможность получить во многих случаях решение с приемлемой точностью при относительно небольших затратах на построение моделей и проведение с ними экспериментов.
4. Эффективность моделирования зависит от того, насколько полно построенная модель соответствует предъявляемым требованиям. Набор этих требований зависит от специфики решаемой задачи, однако, практически во всех случаях в число этих требований входят требования адекватности, универсальности и экономичности.
1. Что такое модель?
2. Что называется моделированием?
3. Где применяются модели?
4. В чем состоит особенность моделирования как методологии?
5. Каковы основные преимущества моделирования?
6. Как классифицируются модели?
7. В чем состоят преимущества и недостатки математических моделей по сравнению с натурными моделями?
8. Как классифицируются математические модели?
9. Чем объясняется широкое распространение математических моделей?
10. Какие бывают математические модели в зависимости от используемого математического аппарата?
11. В чем заключаются отличия линейных моделей от нелинейных?
12. Чем отличается статистическая модель от динамической?
13. Чем отличается детерминированная модель от стохастической?
14. Как различаются модели по критерию модельного времени?
15. Что такое адекватность?
16. Что такое область адекватности?
17. Как можно обосновать адекватность на основе формального сравнения оригинала и модели?
18. Что понимается под требованием универсальности модели?
1. Емельянов А.А., Власова Е.А., Дума Р.В., Емельянова Н.З. Компьютерная имитация экономических процессов: Учебник / Под ред. А.А. Емельянова. – М.: Маркет ДС, 2010. – 464 с.
2. Теория систем и системный анализ в управлении организациями: Справочник / Под ред. В.Н. Волковой и А.А. Емельянова. – М.: Финансы и статистика, 2009. – 848 с.
· познакомиться с возможностями и аппаратом математического моделирования для решения задач анализа и проектирования сложных систем.
· познакомиться теоретическими основами моделирования;
· выяснить основы построения математического описания исследуемых объектов;
· представить основные этапы построения модели и проведение исследований на ее основе.
получите представление о:
· этапах моделирования и их логической последовательности;
· концепциях построения математического описания;
будете знать:
· перечень основных задач, решаемых в процессе моделирования;
· основные термины и понятия, применяемые для построения математического описания;
· шкалы, применяемые для измерения качественных и количественных применяемых в описании модели показателей.
1. Теоретические основы математического моделирования.
2. Измерение свойств.
3. Шкалы измерений.
Философскую концепцию моделирования составляют теория отражения и теория познания, а формально-методическую основу моделирования составляют теория подобия, теория эксперимента, математическая статистика, математическая логика и научные дисциплины, изучающие те предметные области, которые подлежат исследованию методами моделирования.
Согласно математической теории подобия абсолютное подобие может иметь место лишь при замене одного объекта другим точно таким же. При моделировании большинства систем (за исключением, возможно, моделирования одних математических структур другими) абсолютное подобие невозможно, и основная цель моделирования - модель достаточно хорошо должна отображать функционирование моделируемой системы. Одними из основных понятий, используемых в моделировании, являются понятия изоморфизма и гомоморфизма.
Изоморфизм и гомоморфизм (греч. isos — одинаковый, homoios — подобный и morphe — форма) — понятия, характеризующие соответствие между структурами объектов.
Две системы, рассматриваемые отвлеченно от природы составляющих их элементов, являются изоморфными друг другу, если каждому элементу первой системы соответствует лишь один элемент второй и каждой связи в одной системе соответствует связь в другой и обратно. Такое взаимно-однозначное соответствие называется изоморфизм (Рис. 3).
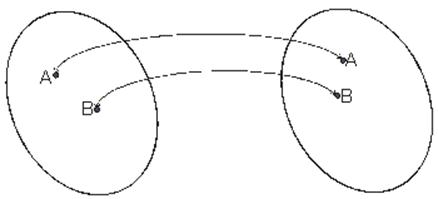
Рис. 3. К понятию изоморфизма
Полный изоморфизм
может быть лишь между абстрактными, идеализированными объектами, например,
соответствие между геометрической фигурой и ее аналитическим выражением в виде
формулы. Например, окружность может быть задана в виде формулы ![]() , или в виде графика в декартовой системе
координат.
, или в виде графика в декартовой системе
координат.
Изоморфизм связан не со всеми, а лишь с некоторыми выбранными в процессе анализа свойствами объектов, которые в других своих отношениях могут отличаться.
Гомоморфизм отличается от изоморфизма тем, что соответствие объектов однозначно лишь в одну сторону. Поэтому гомоморфный образ есть неполное, приближенное отображение структуры оригинала. Примерами гомоморфизма могут служить отношение между картой и местностью или отношение между грамзаписью и ее оригиналом.
Математическая модель представляет собой некоторую абстракцию реального объекта и строится как описание последнего на основе использования основных категорий и понятий. Рассмотрим эти понятия.
Под предметной областью будем понимать мысленно ограниченную область реальной действительности или область идеальных представлений, подлежащую описанию (моделированию) и исследованию. Предметная область состоит из объектов, различаемых по каким-либо признакам (свойствам) и находящихся в определенных отношениях между собой, или взаимодействующих каким-либо образом (Рис. 4).
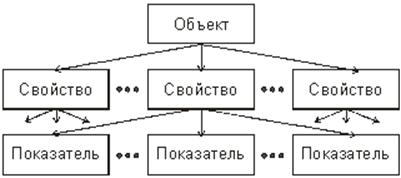
Рис. 4. К понятиям объект, свойство, показатель
Под объектом понимается нечто целое, которое реально существует или возникает в нашем сознании, и обладающее свойствами, значения которых позволяют нам однозначно распознавать это целое. Объект, на котором сосредоточивается внимание субъекта с целью исследования, называется объектом исследования.
Объекты воспринимаются и различаются субъектами лишь постольку, поскольку они обладают характерными свойствами. Свойством называется характерная особенность объекта, которая может быть замечена и оценена субъектом, например, вес, цвет, длина, плотность и тому подобное.
Для оценки исследуемого свойства объекта субъект устанавливает определенную меру называемую показателем свойства. Для каждого показателя определяется множество значений (уровней, или градаций меры свойства), которые присваиваются ему в результате оценивания свойства. Таким образом, свойство объекта является реальностью, а показатель - субъективной мерой этой реальности (если речь идет о реальных объектах).
Показатели всеобщих свойств материальных объектов, таких как пространство и время называются основными показателями. Подавляющее большинство показателей других свойств выражаются через показатели этих основных свойств. Поэтому единицы измерения основных показателей служат основой для построения стандартной системы единиц измерения физических величин и называются основными единицами измерения.
Выражение показателя некоторого свойства через основные единицы измерения, принятые в определенной стандартной системе единиц (мер), называется размерностью данного показателя.
Свойства делятся на внутренние (собственные) свойства объектов, показатели которых называются параметрами, и внешние, представляющие собой свойства среды, связанные некоторыми отношениями с параметрами данного объекта, показатели которых называются факторами.
Свойства объектов выявляются только при их взаимодействии, или при сопоставлении объектов друг с другом. Сопоставление (комбинация) значений показателей, наблюдаемых свойств определенных объектов называется отношением. Говорят, что отношение истинно, если оно подтверждается практическим экспериментом, или логическим выводом. Отношение считается ложным, если оно опровергается практической проверкой, или логическим выводом. В противном случае отношение считается неопределенным. Понятия «истинно», «ложно», «неопределенно» являются логическими значениями любого отношения, результатами субъективной его оценки.
Взаимодействие объектов определяется по результатам измерения значений показателей наблюдаемых свойств этих объектов. Поэтому каждому действию, или взаимодействию присваивается определенный результат. Это может быть значение, или определенная комбинация значений показателей свойств взаимодействующих объектов. Действия над значениями показателей свойств объектов, выполняемые по определенным правилам и приводящие к предполагаемому результату, называются операцией или процедурой.
Значения показателей свойств объектов обозначаются символами из некоторого заранее определенного множества А, называемого алфавитом.
Множество объектов, взаимосвязанных между собой определенными отношениями, и выполняющих определенную общую для них целевую функцию или имеющих общее предназначение, называется системой.
Система, состоящая из алфавита А, строго определенных множеств отношений G, операций Q и предназначенная для символического описания объектов и систем определенного класса, называется формальной системой. Такие системы положены в основу языков математического моделирования.
Энергия является одним из свойств материи, в силу которого все материальные объекты совершают движение в пространстве и времени, находясь в энергетическом взаимодействии и пространственно-временном отношении.
Все материальные объекты существуют в пространстве и во времени, которые также являются всеобщими свойствами материи. Значения показателей пространства и времени входят в состав основных единиц измерения физических свойств объектов.
Так как все свойства объектов изменяются во времени, то любой набор значений показателей этих свойств относится к определенному значению показателя времени. Это отношение называется состоянием объекта.
Значения показателей свойств со временем меняются, в результате чего происходит смена состояний объектов. Акт смены состояний объекта, отнесенный к определенному промежутку времени, называется событием, а последовательность взаимосвязанных событий, происходящих на некотором интервале времени, называется процессом.
Моделирование (в значении «метод», «модельный эксперимент») рассматривается как особая форма эксперимента, эксперимента не над самим оригиналом (это называется простым или обычным экспериментом), а над копией (заместителем) оригинала. В связи с этим одной из основных задач, решаемых в процессе исследований, является задача построения экспериментального образца, т.е., модели исследуемой системы, процесса или явления. Эта задача реализуется в идее совокупности шагов (этапов), целями которых являются сбор данных об исследуемой системе, создание содержательного описания, его формализация, разработка компьютерной программы и обоснование действующей программной модели.
На созданной модели проводится изучение моделируемой системы (оригинала) путем ряда запусков программы (прогонов) на совокупности исходных данных. Собранные сведения анализируются и документируются.
На рис. 5 показаны основные этапы, из которых состоит процесс моделирования.

Рис. 5. Основные этапы математического моделирования
Выполнение шагов описанной процедуры не является в общем случае строго последовательным: в зависимости от получаемых на одном из шагов результатов возможен возврат на предыдущие шаги с целью корректировки их результатов с последующим их повторением. Иначе говоря, процесс моделирования носит итеративный характер.
Понятие измерения было известно в далекой древности, где система товарообмена основывалась на неявной шкале значений. Измерение есть представление свойств (показателей) объекта посредством номеров и чисел.
Номер является материальным или квазиматериальным символом. Номера обладают свойством упорядоченности только благодаря произвольному предписанию или простой договоренности. К номерам неприменимы правила сложения и вычитания.
Число является математическим понятием. Числа обладают свойством упорядоченности благодаря реальным свойствам упорядоченных объектов. В отличие от номеров к числам применимы законы сложения и вычитания.
Номера так же, как и числа, упорядочены; первые — произвольные образом, вторые — на основании двух отношений, существующих между упорядоченными объектами, — отношений, специальное название которых транзитивность и антисимметричность.
Если А находится в некотором отношении к В, а В к С, то А находится в том же отношении к С.
Симметричность.
Если А находится в некотором отношения к В, то В находится в том же отношении к А.
Антисимметричность.
Если А больше В, то В меньше А.
Отношение порядка применимо к свойству твердости: все тела, к которым применимо это понятие, связаны между собой транзитивным и антисимметричным отношением «тверже, чем» или обратным отношением «мягче, чем»; каждое тело, твердость «которого мы хотим определить, либо тверже любого другого тела того же класса, либо мягче него.
Например, отношение «тверже, чем» является транзитивным и антисимметричным. Оно транзитивно потому, что если А оставляет царапину на В, а В — на С, то А оставляет царапину на С. Оно антисимметрично потому, что если А оставляет царапину на В, то В не оставляет царапину на А.
Сложение — это процедура, выполняемая, как правило, над числами и над величинами, характеризующими свойства тел, например вес.
Веса обладают свойством аддитивности. Если тело весом 1 соединить с другим телом того же веса, то образуется тело, вес которого равен сумме весов двух тел, т.е., 2. Можно построить приемлемую процедуру сложения весов, но не удельных весов.
Однако удельный вес не обладает свойством аддитивности: нельзя построить такой процесс соединения двух тел с равным удельным весом, посредством которого было бы образовано тело с удельным весом, большим, чем удельный вес каждого из этих двух тел. Соединяя два тела с равным удельным весом, мы получаем тело с тем же самым удельным весом. Если попытаться применить сложение для удельных весов, то придем к выводу о том, что правило сложения неверно.
Различие между этими двумя характеристиками связано с различием между количеством вещества и его качеством. Количество вещества в теле есть нечто такое, что увеличивается при объединении двух тел, в то время как качеством вещества являются такие признаки, которые посредством объединения двух одинаковых тел вообще не меняются. Поэтому свойства вещества, которые удовлетворяют закону сложения, являются количественной характеристикой, в то время как свойства, для которых закон сложения неверен, есть качественная характеристика вещества.
Цвет является качественной характеристикой, но не количественной, поскольку:
· нельзя подобрать транзитивное и антисимметричное отношения, которые выражали бы различия в цвете;
· для цветов не существует естественной упорядоченности, которая дала бы нам возможность присвоить им номера, если не считать произвольной договоренности.
Произвольной в том смысле, что эта договоренность не следует из эксперимента. Порядковый номер, соответствующий той или иной степени твердости, несет в себе определенные экспериментальные факты, чего нельзя сказать про порядковый номер цвета. Именно поэтому мы считаем, что твердость есть подлежащее измерению свойство в том смысле, в котором свойство цвета не является измеримым.
Таким образом:
· Существует два вида свойств: количественные и качественные.
· Измерение применимо к обоим видам, но количественные свойства допускают измерение более высокого уровня, чем качественные.
· Уровень измерения свойства зависит от характеристик последнего — транзитивности, симметричности, аддитивности и т. п., что определяет выбор используеммой шкалы измерения.
Переменные различаются тем, насколько хорошо они могут быть измерены или, другими словами, как много измеряемой информации обеспечивает шкала их измерений. В каждом измерении присутствует некоторая ошибка, определяющая границы количества информации, которое можно получить в данном измерении.
Другим фактором, определяющим количество информации, которое содержится в переменной, является тип шкалы, в которой проведено измерение. Различают номинальную, порядковую (ординальную), интервальную и относительную шкалы. Соответственно, имеется четыре типа переменных:
1) номинальная;
2) порядковая (ординальная);
3) интервальная;
4) относительная (отношений).
Шкала, содержащая только категории; данные в ней не могут упорядочиваться, с ними не могут быть произведены никакие арифметические действия.
Номинальные переменные используются только для качественной классификации. Это означает, что данные переменные могут быть измерены только в терминах принадлежности к некоторым, существенно различным классам; при этом вы не сможете определить количество или упорядочить эти классы. Например, вы сможете сказать, что два индивидуума различимы в терминах переменной А (например, индивидуумы принадлежат к разным национальностям). Данные, измеренными в этой шкале, не могут упорядочиваться, с ними не могут быть произведены никакие арифметические действия.
Номинальная шкала состоит из названий, категорий, имен для классификации и сортировки объектов или наблюдений по некоторому признаку.
Для номинальной шкалы применимы только операции равно (=) и не равно (≠).
Часто номинальные переменные называют категориальными. Примерами могут служить профессия, город проживания, семейное положение или пол человека.
Шкала, в которой числа присваивают объектам для обозначения относительной позиции объектов, но не величины различий между ними.
Эта шкала дает возможность ранжировать значения переменных. Измерения же в порядковой шкале содержат информацию только о порядке следования величин, но не позволяют сказать насколько одна величина больше другой, или насколько она меньше другой.
Порядковые переменные иногда также называют ординальными.
Для порядковой шкалы применимы операции равно (=), не равно (≠), больше (>), меньше (<).
Само расположение шкал в следующем порядке: номинальная, порядковая, интервальная является примером порядковой шкалы. Другими примерами могут служить:
· место (1, 2, 3…), занятое командой на спортивном соревновании;
· социальный статус семьи (можно утверждать, что верхний средний уровень выше среднего уровня, однако нельзя сказать, что разница между ними составляет, например, 30%).
Шкала, разности, между значениями которой могут быть вычислены, однако их отношения не имеют смысла.
Интервальные переменные позволяют не только упорядочивать объекты измерения, но и численно выразить и сравнить различия между ними. Например, температура, измеренная в градусах Фаренгейта или Цельсия, образует интервальную шкалу. Мы можем не только сказать, что температура 40 градусов выше, чем температура 30 градусов, но и что увеличение температуры с 20 до 40 градусов вдвое больше увеличения температуры от 30 до 40 градусов.
Эта шкала позволяет находить разницу между двумя величинами, обладает свойствами номинальной и порядковой шкал, а также позволяет определить количественное изменение признака.
Номинальная и порядковая шкалы являются дискретными, а интервальная шкала - непрерывной, она позволяет осуществлять точные измерения признака и производить арифметические операции сложения, вычитания, умножения, деления.
Для интервальной шкалы применимы операции равно (=), не равно (≠), больше (>), меньше (<),сложения (+) и вычитания (-).
Например, если температура воды в море утром - 19 градусов, вечером - 24, т.е. вечерняя на 5 градусов выше, то нельзя сказать, что она в 1,26 раз выше.
Шкала, в которой есть определенная точка отсчета и возможны отношения между значениями шкалы. Относительные переменные очень похожи на интервальные переменные. В дополнение ко всем свойствам переменных, измеренных в интервальной шкале, их характерной чертой является наличие определенной точки абсолютного нуля, таким образом, для этих переменных являются обоснованными предложения типа: X в два раза больше, чем Y. Типичными примерами шкал отношений являются измерения времени или пространства. Например, температура по Кельвину образует шкалу отношения, и мы можем не только утверждать, что температура 200 градусов выше, чем 100 градусов, но и что она вдвое выше. Интервальные шкалы (например, шкала Цельсия) не обладают данным свойством шкалы отношения. Заметим, что в большинстве статистических процедур не делается различия между свойствами интервальных шкал и шкал отношения.
Для относительной шкалы применимы операции равно (=), не равно (≠), больше (>), меньше (<), сложения (+), вычитания (-), умножения (*) и деления (/).
Относительные и интервальные шкалы являются числовыми.
Таблица 1 и Таблица 2 поясняют использование шкал в разных задачах.
Таблица 1.
Использование различных шкал для сбора данных о кадровом составе
|
Порядковый номер |
Профессия (номинальная шкала) |
Средний бал (интервальная шкала) |
Образование (порядковая шкала) |
|
1 |
Слесарь |
22 |
Среднее |
|
2 |
Ученый |
55 |
Высшее |
|
3 |
Учитель |
47 |
Высшее |
Таблица 2.
Использование различных шкал для измерений погодных условий
|
Дата измерения |
Облачность (номинальная шкала) |
Температура (интервальная шкала) |
Сила ветра (порядковая шкала) |
|
1 сентября |
Облачно |
22 Сº |
Сильный |
|
2 сентября |
Пасмурно |
17 Сº |
Слабый |
|
3 сентября |
Ясно |
23 Сº |
Очень сильный |
1. Методология моделирования основывается на нескольких фундаментальных философских и математических теориях. Основными понятими, используемыми в моделировании, являются понятия изоморфизма и гомоморфизма, опеределяющих отношение между объектом и моделью.
2. Процесс построения и использования модели состоит из последовательности определенных шагов с четко выраженным результатом выполнения каждого шага. В силу сложности задачи, неполноты сведений и возможной неоднозначности логика выполнения шагов может носить итеративный характер, с возвратом на предыдущие шаги в случае получения неудовлетворительного результата, либо выявления ошибок или неточностей предыдущих шагов.
3. Математическое описание моделируемого объекта разрабатывается на основе взаимосвязанной совокупности характеризующих объект показателей. Модель включает наиболее существенное подмножество этих показателей, которые могут относиться как к количественным, так и качественным.
4. Для измерения показателей используются шкалы. В зависимости от типа показателей и потребностей модели для измерения показателя может выбираться та или иная шкала, позволяющая получить разный объем сведений относительно моделируемого объекта и выполнять над показателями математические операции.
1. Какие теории образуют концептуальный базис моделирования?
2. Что такое изоморфизм? Приведите пример.
3. Что такое гомоморфизм? Приведите пример.
4. Что называется свойством?
5. На какие категории подразделяются свойства?
6. Что такое показатель?
7. Что понимается под отношением?
8. Что понимается под состоянием объекта?
9. Что такое называется событием?
10. Что такое процесс?
11. Назовите основные этапы процесса моделирования.
12. Что называется номером?
13. Что называется числом?
14. В чем заключается различие между номером и числом?
15. Объясните разницу между количественной и качественной характеристикой.
16. Что представляет собой номинальная шкала?
17. Какие операции применимы в номинальной шкале.
18. Что представляет собой порядковая шкала?
19. Какие операции применимы в порядковой шкале.
20. Что представляет собой интервальная шкала?
21. Какие операции применимы в интервальной шкале?
22. Что представляет собой шкала отношений?
23. Какие операции применимы в шкале отношений?
1. Анфилатов В.С., Емельянов А.А., Кукушкин А.А. Системный анализ в управлении / Под ред. А.А. Емельянова. – М.: Финансы и статистика, 2009. – 368 с.
2. Бусленко Н.П. Моделирование сложных систем. – М.: Наука, 1968. – 356 с.
3. Емельянов А.А., Власова Е.А., Дума Р.В., Емельянова Н.З. Компьютерная имитация экономических процессов: Учебник / Под ред. А.А. Емельянова. – М.: Маркет ДС, 2010. – 464 с.
4. Теория систем и системный анализ в управлении организациями: Справочник / Под ред. В.Н. Волковой и А.А. Емельянова. – М.: Финансы и статистика, 2009. – 848 с.
· познакомиться с пуассоновским потоком заявок, имеющим большое значения для моделирования широкого класса систем и процессов;
· изучить математический аппарат проверки гипотез для решения задач этапов сбора данных и обработки результатов моделирования.
· познакомиться с постановкой задачи проверки статистических гипотез применительно к их использованию в моделировании;
· понять какие свойства потока позволяют относить поток к классу пуассоновских;
· овладеть способом определения характеристик потока с помощью формулы Пуассона.
получите представление о:
· постановке и примерах задач проверки гипотез;
· критериях, применяемых при оценивании гипотез;
· подходах к сбору исходных данных и анализу результатов моделирования в системах потоками заявок;
будете знать:
· как практически применить критерий проверки гипотезы к реальной задаче, возникающей при моделировании.
1. Постановка задачи проверки гипотез.
2. Пуассоновский поток.
3. Пример проверки гипотез.
Любое исследование системы методом моделирования основывается на использовании как количественных, так и качественных сведений относительно изучаемой системы. Одним из первых и наиболее важных этапов процесса моделирования является этап сбора исходных данных и приведение их к виду наиболее полно соответствующему требованиям удобства их последующего использования в модели. Например, исследование систем массового обслуживания, о которых будет идти речь далее, начинается с изучения того, что необходимо обслуживать, иначе говоря, с изучения характеристик входящего потока заявок. В нетривиальных случаях требуется также обследование самой системы массового обслуживания с целью нахождения характеристик обслуживания (потока обслуживания).
Для каких-либо свойств или показателей системы часто приходится делать некоторое допущение относительно характера и параметров математической зависимости, описывающей значения показателя, основываясь на результатах наблюдения за значением показателя. После этого принятое допущение подвергается проверке. Решение этой задачи носит название проверки статистических гипотез.
Существуют различные методы проверки статистических гипотез. Наиболее широко на практике используются критерии:
·
Пирсона, или ![]() (хи-квадрат).
(хи-квадрат).
· Крамера-фон Мизеса.
· Колмогорова-Смирнова.
Критерий согласия ![]() предпочтителен в тех случаях, если объемы выборок (число значений,
полученных или измеренных в результате наблюдений) N, в отношении
которых проводится анализ, велики. Это мощное средство, если N > 100
значений.
предпочтителен в тех случаях, если объемы выборок (число значений,
полученных или измеренных в результате наблюдений) N, в отношении
которых проводится анализ, велики. Это мощное средство, если N > 100
значений.
Следует, однако, заметить, что в ряде случаев, в частности, при анализе экономических ситуаций, бывает довольно трудно или невозможно найти 100 одинаковых процессов, развивающихся с различными исходными данными. Сложность заключается не только в том, что не бывает одинаковых объектов экономики, а и втом, что к исходным данным относятся не только исходные вероятностные данные и особенности структуры объекта. Влияние на процесс оказывает также сценарий развития процессов в этом объекте и в тех объектах внешней среды, с которыми он взаимодействует (процессы, протекающие на рынке, указы правительства, принятие новых законов, требования налоговых органов, платежи в бюджеты различных уровней).
Критерий Крамера-фон Мизеса дает хорошие результаты при малых объемах выборок, обычно, для N < 10. Однако для N < 10 независимо от применяемого метода вопрос о доверительной вероятности при проверке статистической гипотезы решается плохо - эта вероятность мала при значительных размерах доверительных интервалов.
Для выборок с объемами в пределах 10 < N < 100 согласно многим исследованиям хорошие результаты дает критерий Колмогорова-Смирнова. Он применяется в тех случаях, когда проверяемое распределение непрерывно и известны среднее значение и дисперсия испытуемой совокупности.
Рассмотрим подробнее методику
использования критерия ![]() на
конкретном примере, предварительно познакомившись с часто встречающимся в моделях
стохастических систем классом потоков, называемым пуассоновским.
на
конкретном примере, предварительно познакомившись с часто встречающимся в моделях
стохастических систем классом потоков, называемым пуассоновским.
Поток требований называют однородным, если:
· все требования потока обслуживаются в системе массового обслуживания одинаково;
· рассмотрение требований (событий) потока, которые по своей природе могут быть различными, ограничивается рассмотрением моментов времени их поступления.
Поток называется регулярным, если события в потоке следуют один за другим через интервалы времени одинаковой длительности.
Функция f(х) плотности распределения вероятности случайной величины Т, обозначающей интервал времени между событиями, для регулярного потока имеет вид:
![]()
где
![]() - дельта функция;
- дельта функция;
![]() - математическое ожидание случайной величины T.
- математическое ожидание случайной величины T.
Дисперсия интервала между событиями регулярного потока
(моментами поступления требований) D[T] равна 0,
а интенсивность наступления событий в потоке (среднее число требований в
единицу времени) ![]() равна
равна ![]() .
.
Поток называется случайным, если события в потоке следуют один за другим через интервалы времени случайной длительности.
Случайный поток может быть описан как случайный вектор, который, в свою очередь, может быть задан одним из двух способов:
1)
Функцией распределения моментов
наступления событий ![]() :
:
![]()
где
ti – значение моментов наступления Ti(i=1, n).
2) Функцией распределения интервалов между наступлением последовательных событий τ1, τ2, … τn:
![]() ,
,
где
![]() i - значения интервалов между событиями τi(i=1, n).
i - значения интервалов между событиями τi(i=1, n).
В последнем случае моменты наступления событий могут при необходимости быть найдены из рекуррентных соотношений:
![]()
![]()
![]()
где
t0 - момент наступления первого события потока.
Поток называется стационарным, если вероятность попадания того или иного числа событий на элементарный участок времени длиной τ зависит только от длины участка и не зависит от того, где именно на оси t расположен этот участок.
Поток событий называется потоком без последействия, если для любых непересекающихся участков времени число событий, попадающих на один из них, не зависит от того, сколько событий попало на другой.
Поток событий называется ординарным, если вероятность попадания на элементарный участок двух или более событий пренебрежимо мала по сравнению с вероятностью попадания одного события.
Поток событий, обладающий всеми тремя указанными свойствами, называется простейшим, или стационарным пуассоновским потоком.
Пуассоновский поток событий тесно связан с известным из теории вероятностей распределением Пуассона: число событий потока, попадающих на временной интервал некоторой величины, распределено по закону Пуассона.
Если на временной оси t, где наблюдается поток событий, выделить некоторый участок времени длины τ, начинающийся в момент t0 и заканчивающийся в момент t0 + τ, то нетрудно доказать, что вероятность попадания на этот участок ровно m событий выражается формулой:
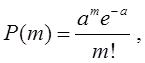 (1)
(1)
где
а — среднее число событий, приходящееся на участок τ;
е — основание натуральных логарифмов (2,71828 … ).
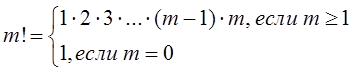
Для стационарного (простейшего) пуассоновского потока величина а равна интенсивности потока λ, умноженной на длину интервала:
![]() ,
,
где интенсивность, или плотность потока λ есть среднее число событий, приходящихся на единичный временной интервал. В зависимости от физической природы изучаемой системы интенсивность может иметь различную размерность, например, чел/мин, руб/день, кг/час, запросов/сек, документов/сутки, отправлений/сутки и т.д.
Функция распределения
![]()
представляющая собой по определению вероятность того, что случайная величина Т (интервал времени между событиями) не превысит значения t, имеет для пуассоновского потока следующий вид:
![]() (2)
(2)
Такой закон распределения называется показательным (или экспоненциальным) с плотностью λ. Величина λ называется также параметром показательного закона.
Математическое ожидание случайной величины
![]() равно:
равно:
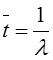 , (3)
, (3)
а дисперсия составляет:
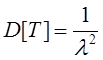 (4)
(4)
Среднеквадратическое отклонение случайной
величины ![]() находится как квадратный корень из
дисперсии:
находится как квадратный корень из
дисперсии:
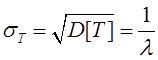 (5)
(5)
Как нетрудно видеть, математическое ожидание величины Т равно ее среднеквадратическому отклонению, что является характерной особенностью экспоненциального распределения.
Таким образом, вероятность появления m событий в заданном промежутке времени описывается пуассоновским распределением, а вероятность того, что временные интервалы между событиями потока не превзойдут некоторого наперед заданного значения, описывается экспоненциальным распределением. Это различные описания одного и того же стохастического процесса.
Решение многих задач анализа и проектирования систем (в частности, систем массового обслуживания) намного упрощается в случаях, когда входящий поток и поток обслуживания являются простейшими (пуассоновскими). Покажем, каким образом можно вынести суждение о принадлежности наблюдаемого потока к пуассоновскому (напомним еще раз, что потоки этого типа имеют очень важное значение для решения практических задач, в чем вы сможете убедиться далее).
Предположим, что проводилось наблюдение за потоком посетителей в отделении банка в течение 10 дней его работы. Результаты (число пришедших в течение часа в банк людей) представлены в таблице:
|
Часы
Дни |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
2 |
4 |
2 |
3 |
4 |
3 |
5 |
2 |
|
|
2 |
3 |
2 |
3 |
2 |
7 |
2 |
3 |
3 |
|
3 |
1 |
3 |
4 |
3 |
4 |
6 |
4 |
2 |
|
4 |
4 |
4 |
4 |
5 |
9 |
3 |
4 |
4 |
|
5 |
2 |
1 |
3 |
7 |
3 |
6 |
2 |
3 |
|
6 |
3 |
2 |
3 |
4 |
5 |
5 |
3 |
2 |
|
7 |
4 |
3 |
4 |
3 |
8 |
3 |
4 |
3 |
|
8 |
1 |
2 |
2 |
4 |
3 |
4 |
2 |
4 |
|
9 |
3 |
4 |
6 |
3 |
4 |
2 |
4 |
2 |
|
10 |
2 |
2 |
3 |
5 |
6 |
4 |
2 |
5 |
Определим интенсивность входящего потока покупателей за час работы отделения и, используя критерий Пирсона с уровнем значимости α=0,05, подвергнем проверке гипотезу о том, что поток описывается пуассоновским законом распределения.
Сгруппируем данные по числу клиентов банка k, посетивших отделение в течение часа, а результаты представим в виде таблицы:
|
k |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
fk |
3 |
19 |
23 |
21 |
6 |
4 |
2 |
1 |
1 |
Предварительно заполнив в
таблице для удобства вычислений дополнительную строку со значениями
произведения ![]()
|
k |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
Σ |
|
fk |
3 |
19 |
23 |
21 |
6 |
4 |
2 |
1 |
1 |
80 |
|
k × fk |
3 |
38 |
69 |
84 |
30 |
24 |
14 |
8 |
9 |
279 |
найдем величину
интенсивности потока ![]() :
:
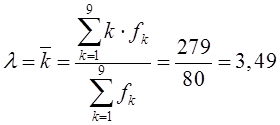 .
.
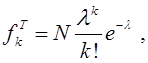
где
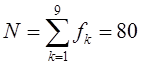 .
.
Находим и заносим в строку fТ теоретические значения частот:
|
k |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
Σ |
|
fk |
3 |
19 |
23 |
21 |
6 |
4 |
2 |
1 |
1 |
80 |
|
k × fk |
3 |
38 |
69 |
84 |
30 |
24 |
14 |
8 |
9 |
279 |
|
fТ |
8,53 |
14,88 |
17,29 |
15,08 |
10,52 |
6,11 |
3,05 |
1,33 |
0,51 |
|
Вычислим и занесем в строку таблицы:
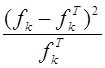 .
.
Значения, стоящие в числителе выражения под знаком суммы в формуле:
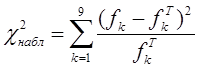 .
.
Для наблюдаемого значения критерия Пирсона:
|
k |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
Σ |
|
fk |
3 |
19 |
23 |
21 |
6 |
4 |
2 |
1 |
1 |
80 |
|
k × fk |
3 |
38 |
69 |
84 |
30 |
24 |
14 |
8 |
9 |
279 |
|
fТ |
8,53 |
14,88 |
17,29 |
15,08 |
10,52 |
6,11 |
3,05 |
1,33 |
0,51 |
|
|
|
3,59 |
1,14 |
1,88 |
2,33 |
1,94 |
0,73 |
0,36 |
0,08 |
0,46 |
12,51 |
В результате получаем
наблюдаемое значение![]() .
.
По заданному уровню значимости α=0,05 и числу степеней свободы:
ν = n-2,
где
n - число групп в ряду (в нашем случае n=9) по
таблице значений критических точек ![]() распределения
находим
распределения
находим ![]() .
.
Поскольку ![]() (12,51 < 14,07) не отвергаем гипотезу о
том, что входящий поток описывается пуассоновским законом распределения с
интенсивностью
(12,51 < 14,07) не отвергаем гипотезу о
том, что входящий поток описывается пуассоновским законом распределения с
интенсивностью ![]() =3,49 час-1.
=3,49 час-1.
Вид теоретической и экспериментальной зависимостей для рассмотренного примера показан на диаграмме рис. 6:
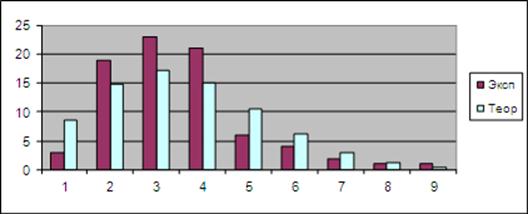
Рис. 6. Графики теоретической и экспериментальной зависимостей частот числа заявок входящего потока
Предположим теперь, что проводилось наблюдение за временем обслуживания клиентов отделения банка кассиром, в результате чего получена таблица для частот интервалов следующего вида:
|
|
tмин |
tмакс |
f |
|
1 |
0 |
5 |
17 |
|
2 |
5 |
10 |
20 |
|
3 |
10 |
15 |
19 |
|
4 |
15 |
20 |
11 |
|
5 |
20 |
25 |
9 |
|
6 |
25 |
30 |
6 |
|
7 |
30 |
35 |
3 |
|
8 |
35 |
40 |
1 |
Определим среднее время ![]() и интенсивность μ обслуживания клиентов,
после чего проверим на уровне значимости α=0,05 гипотезу о том, что время
и интенсивность μ обслуживания клиентов,
после чего проверим на уровне значимости α=0,05 гипотезу о том, что время ![]() распределено по показательному закону,
используя для этого критерий Пирсона.
распределено по показательному закону,
используя для этого критерий Пирсона.
1) Находим среднее значение каждого временного интервала по формуле:
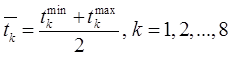 ,
,
Значения заносим в столбец, добавляемый к таблице справа:
|
|
tмин |
tмакс |
f |
|
|
1 |
0 |
5 |
17 |
2,5 |
|
2 |
5 |
10 |
20 |
7,5 |
|
3 |
10 |
15 |
19 |
12,5 |
|
4 |
15 |
20 |
11 |
17,5 |
|
5 |
20 |
25 |
9 |
22,5 |
|
6 |
25 |
30 |
6 |
27,5 |
|
7 |
30 |
35 |
3 |
32,5 |
|
8 |
35 |
40 |
1 |
37,5 |
2)
Находим среднее время обслуживания
![]()
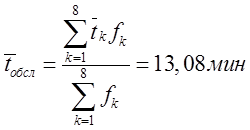 ,
,
и интенсивность μ обслуживания
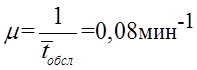 ,
,
Подсчитаем и занесем в
ячейки отдельного столбца произведения![]() ,
входящие в выражение для среднего времени:
,
входящие в выражение для среднего времени:
|
|
tмин |
tмакс |
f |
|
|
|
1 |
0 |
5 |
17 |
2,5 |
42,5 |
|
2 |
5 |
10 |
20 |
7,5 |
150,0 |
|
3 |
10 |
15 |
19 |
12,5 |
238,0 |
|
4 |
15 |
20 |
11 |
17,5 |
193,0 |
|
5 |
20 |
25 |
9 |
22,5 |
203,0 |
|
6 |
25 |
30 |
6 |
27,5 |
165,0 |
|
7 |
30 |
35 |
3 |
32,5 |
97,5 |
|
8 |
35 |
40 |
1 |
37,5 |
37,5 |
|
Σ |
|
|
|
|
|
3) По формуле
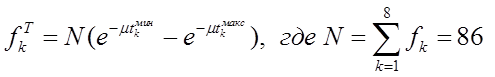 ,
,
находим теоретические частоты:
|
|
tмин |
tмакс |
f |
|
|
fТ |
|
1 |
0 |
5 |
17 |
2,5 |
42,5 |
27,32 |
|
2 |
5 |
10 |
20 |
7,5 |
150,0 |
18,64 |
|
3 |
10 |
15 |
19 |
12,5 |
238,0 |
12,72 |
|
4 |
15 |
20 |
11 |
17,5 |
193,0 |
8,68 |
|
5 |
20 |
25 |
9 |
22,5 |
203,0 |
5,92 |
|
6 |
25 |
30 |
6 |
27,5 |
165,0 |
4,04 |
|
7 |
30 |
35 |
3 |
32,5 |
97,5 |
2,76 |
|
8 |
35 |
40 |
1 |
37,5 |
37,5 |
1,88 |
|
Σ |
|
|
86 |
|
|
|
4)
Вычислим и занесем в отдельный
столбец таблицы значения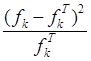 , входящие в
выражение под знаком суммы в формуле
, входящие в
выражение под знаком суммы в формуле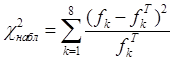 для
наблюдаемого значения критерия Пирсона:
для
наблюдаемого значения критерия Пирсона:
|
|
tмин |
tмакс |
f |
|
fТ |
|
|
1 |
0 |
5 |
17 |
2,5 |
27,32 |
3,90 |
|
2 |
5 |
10 |
20 |
7,5 |
18,64 |
0,10 |
|
3 |
10 |
15 |
19 |
12,5 |
12,72 |
3,10 |
|
4 |
15 |
20 |
11 |
17,5 |
8,68 |
0,62 |
|
5 |
20 |
25 |
9 |
22,5 |
5,92 |
1,60 |
|
6 |
25 |
30 |
6 |
27,5 |
4,04 |
0,95 |
|
7 |
30 |
35 |
3 |
32,5 |
2,76 |
0,02 |
|
8 |
35 |
40 |
1 |
37,5 |
1,88 |
0,41 |
|
Σ |
|
|
86 |
|
|
10,7 |
Просуммировав, получим![]() .
.
5)
По заданному уравнению значимости
α=0,05 и числу степеней свободы ν = n–2 , где n – размер
выборки (число групп в ряду, в нашем случае n=8) в таблице критических чисел
![]() находим
находим ![]() .
.
6)
Поскольку![]() (10,7<12,59), гипотезу о том, что время обслуживания
описывается экспоненциальным законом распределения с интенсивностью
(10,7<12,59), гипотезу о том, что время обслуживания
описывается экспоненциальным законом распределения с интенсивностью![]() , не отвергаем.
, не отвергаем.
Вид теоретической и экспериментальной зависимостей для рассмотренного примера показан на диаграмме:
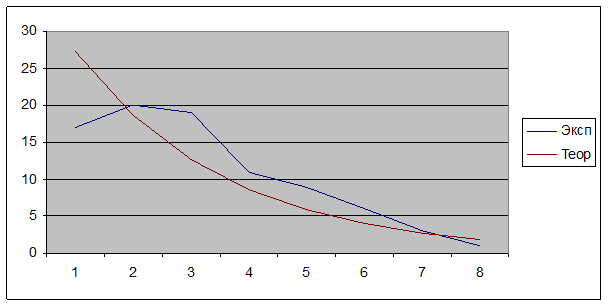
Рис. 7. Графики теоретической и экспериментальной зависимостей частот продолжительности обслуживания заявки
1. Для эффективного решения задач на этапах сбора исходных данных для моделирования и анализа полученных результатов необходимо применять специальные методы. Одним из наиболее распространенных методов описания входных и выходных показателей является метод оценивания статистических гипотез.
2. Существуют несколько критериев, которые могут применяться для проверки гипотез. Выбор конкретного критерия зависит от условий, в которых производится оценивание гипотезы, в первую очередь, от объема выборки используемых для оценивания данных.
3. Для моделирования широкого класса систем и процессов необходимо строить математическое описание циркулирующих потоков объектов различного класса (информационных, материальных). Потоки могут характеризоваться различными свойствами, которые обусловливают тот или иной вид их математического описания.
4. Важным частным случаем потоков в моделируемых системах и процессах является пуассоновский поток. Поэтому в практических задачах целесообразно подвергать проверке гипотезу о принадлежности наблюдаемого потока к пуассоновскому, применяя тот или иной критерий.
1. В чем состоит сущность проверки статистических гипотез, и для каких задач моделирования она применяется?
2. Какие критерии проверки гипотез вы знаете?
3. От чего зависит выбор того или иного критерия проверки гипотез?
4. Что такое пуассоновский поток?
5. Как записывается и что позволяет найти формула Пуассона?
6. Как называется и что означает параметр пуассоновского закона?
7. Какому закону распределения подчиняются интервалы между поступлением отдельных заявок потока?
8. Как найти вероятность того, что в течение определенного интервала поступит не более определенного числа требований?
9. Чему равно математическое ожидание интервала времени между событиями в пуассоновском потоке?
10. Чему равно среднеквадратическое отклонение интервала времени между событиями в пуассоновском потоке?
11. Для чего нужно аппроксимировать экспериментальные данные относительно потока заявок и времени обслуживания в системе массового обслуживания теоретическими зависимостями?
12. Какие шаги нужно выполнить, чтобы построить теоретическую зависимость?
13. Зачем нужно проводить оценку статистической значимости результата?
1. Бусленко Н.П. Моделирование сложных систем. – М.: Наука, 1968. – 356 с.
2. Емельянов А.А., Власова Е.А., Дума Р.В. Имитационное моделирование экономических процессов / Под ред. А.А. Емельянова. – М.: Финансы и статистика, 2009. – 480 с.
3. Теория систем и системный анализ в управлении организациями: Справочник / Под ред. В.Н. Волковой и А.А. Емельянова. – М.: Финансы и статистика, 2009. – 848 с.
Цели изучения темы:
· познакомиться с понятием марковского процесса;
· познакомиться с математическим аппаратом моделирования дискретно протекающих марковских процессов.
Задачи изучения темы:
· изучить способ математического описания марковских процессов;
· научиться определять характеристики марковских процессов с дискретным временем и дискретным множеством состояний.
Успешно изучив тему, Вы:
получите представление о:
· сущности марковских процессов и их классификации;
· как формулируются задача в терминах марковского процесса;
· способах построения математической модели и нахождения с ее помощью значений нужных показателей;
будете знать:
· как описать протекающие процессы с помощью графа состояний и переходов;
· как найти вектор вероятностей состояния процесса на определенном шаге;
· как вычислить предельные вероятности процесса.
Вопросы темы:
1. Понятие марковского процесса.
2. Классификация марковских процессов.
3. Граф состояний и переходов.
4. Марковский процесс с дискретными состояниями и дискретным временем.
5. Предельные вероятности цепи Маркова.
Постановка многих задач анализа и, в особенности, проектирования систем связаны с необходимостью проведения оценивания количественных показателей протекающих в системе процессов. Часто поведение этих развивающихся во времени процессов в силу действия различных случайных факторов не удается исследовать во всех деталях. Следствием этого является невозможность в отличие от детерминированных систем однозначно предсказать поведение системы в какой-то момент в будущем. Такие системы и процессы носят название стохастических (от греческого στοχαστική – умеющий угадывать). Их анализ целесообразно проводить, рассматривая их как случайные процессы, ход и исход которых зависят от ряда случайных факторов, сопровождающих их развитие.
Для нахождения числовых значений нужных параметров применяются как аналитические, так и имитационные модели. В настоящей и следующей теме будет рассмотрен подход на основе аналитических моделей. Построение аналитической модели в случае стохастических процессов означает необходимость построения некоторой вероятностной модели явления, в которой будут учтены обусловливающие его развитие случайные факторы.
Для математического описания многих случайных процессов может быть применен аппарат, разработанный в теории вероятностей для так называемых марковских случайных процессов.
Случайный процесс, протекающий в системе S, называется марковским (или процессом без последействия), если он обладает следующим свойством: для каждого момента времени t0 вероятность любого состояния системы в будущем (при t>t0) зависит только от ее состояния в настоящем (при t= t0) и не зависит от того, когда и каким образом система пришла в это состояние (т.е., как развивался процесс в прошлом).
Другими словами, в марковском случайном процессе будущее развитие зависит только от его настоящего состояния и не зависит от «предыстории» процесса.
Марковские случайные процессы делятся на классы. Основными классифицирующими признаками являются:
· множество состояний, в которых может находиться система;
· моменты времени, в которых происходит изменение состояния системы.
Случайный процесс называется процессом с дискретными состояниями, если возможные состояния системы S1, S2, S3, ... можно перечислить (перенумеровать) одно за другим, а сам процесс состоит в том, что время от времени система S скачком (мгновенно) переходит из одного состояния в другое.
Кроме процессов с дискретными состояниями существуют случайные процессы с непрерывными состояниями: для этих процессов характерен постепенный, плавный переход из состояния в состояние. Например, процесс изменения напряжения в осветительной сети представляет собой случайный процесс с непрерывными состояниями.
Если переходы системы из состояния в состояние возможны только в определенные моменты времени t1, t2, t3, … , то марковский процесс относится к процессам с дискретным временем. В противном случае имеет место процесс с непрерывным временем.
Анализ случайных процессов с дискретными состояниями обычно проводится с помощью графа состояний и переходов (ГСП).
Пусть имеется система S с n дискретными состояниями:
S1, S2, S3 , … , Sn
Каждое состояние изображается окружностью или прямоугольником (вершина), а возможные переходы из состояния в состояние («перескоки») — стрелками (дугами), соединяющими эти вершины (рис. 8а).
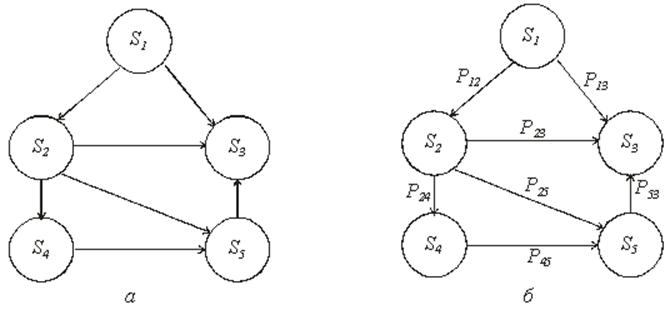
Рис. 8. Пример неразмеченного (а) и размеченного (б) ГСП
Заметим, что стрелками можно отмечать только непосредственные переходы из состояния в состояние; если система может перейти из состояния S1 в S5 только через S2, то стрелками отмечаются только переходы S1—S2 и S2—S5, но не S1—S5.
Удобно также пользоваться размеченным графом, который графически изображает не только возможные состояния системы и возможные переходы из состояния в состояние, но также и значения вероятностей перехода (рис. 8 б), о которых речь будет идти ниже.
Пусть система S может находиться в состояниях:
S1, S2, S3, … , Sn
и изменения состояния системы возможны только в моменты:
t1, t2, t3, … , tn
Будем называть эти моменты шагами, или этапами процесса и рассматривать протекающий в системе S случайный процесс как функцию целочисленного аргумента m = 1, 2, ... k, ... , обозначающего номер шага.
Указанный случайный процесс состоит в том, что в последовательные моменты времени t1, t2, ... , tk, ... система S оказывается в тех или иных состояниях. Процесс, происходящий в системе, можно представить как последовательность (цепочку) событий, например:
![]()
называемую марковской цепью, где для каждого шага вероятность перехода из любого состояния Si в любое Sj не зависит от того, когда и как система пришла в состояние Si .
Марковскую цепь можно описать с помощью вероятностей состояний, в которых находится система на каком-то шаге. Пусть в любой момент времени (после любого шага) система может пребывать в одном из состояний:
S1, S2, S3, … , Sn
т.е., в результате шага k осуществится одно из полной группы несовместных событий:
![]() .
.
Обозначив вероятности этих событий для k -го шага через
![]()
легко видеть, что для каждого шага k
![]()
поскольку ![]() ,
представляют собой вероятности появления полной группы событий.
,
представляют собой вероятности появления полной группы событий.
Вероятности ![]() называются
вероятностями состояния.
называются
вероятностями состояния.
Для любого шага (момента времени t1, t2, ... tk, ... или номера 1, 2, ... , k, ...) существуют некоторые вероятности перехода системы из любого состояния в любое другое (некоторые из них равны нулю, если непосредственный переход за один шаг невозможен), а также вероятность задержки системы в данном состоянии. Эти вероятности называются переходными вероятностями марковской цепи.
Если значения переходных вероятностей не зависят от номера шага, то марковская цепь называется однородной, или стационарной. В противном случае марковская цепь является неоднородной, или нестационарной.
Если из состояния Si не исходит ни одной стрелки (переход из него ни в какое другое состояние невозможен, например, S3 графа рис. 8), соответствующая вероятность задержки Рii равна единице.
Графу системы, содержащему n вершин, можно поставить в соответствие матрицу n×n, элементами которой являются вероятности переходов pij между вершинами графа, называемую матрицей вероятностей переходов:
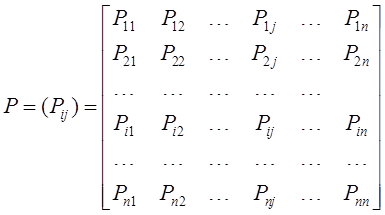 (1)
(1)
Элементы матрицы переходов, означающие вероятности переходов в системе за один шаг, удовлетворяют условиям:
![]() (2)
(2)
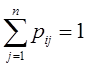 (3)
(3)
Условие (2) выражает ограничение, накладываемое на значение вероятности, а
условие (3) означает, что система S обязательно либо переходит из
какого-то состояния Si в
другое состояние, либо остается в состоянии Si (иначе говоря, события ![]() образуют
полную группу событий).
образуют
полную группу событий).
Обычно на графе вероятности перехода системы из одного
состояния в то же самое не отмечаются, так как каждая
из них дополняет до единицы сумму переходных вероятностей, соответствующих всем
стрелкам, исходящим из данного состояния. Например, для графа рис. 8 б значения
переходных вероятностей ![]() будут равны:
будут равны:
![]()
![]()
![]()
![]()
![]() .
.
При рассмотрении конкретных систем удобно сначала построить граф состояний, затем определить вероятность переходов системы из одного состояния в то же самое (исходя из требования равенства единице суммы элементов строк матрицы), а потом составить матрицу переходов системы.
Имея размеченный ГСП (или, что равносильно, матрицу переходных вероятностей) и зная начальное состояние системы, можно найти вероятности состояний р1(k), р2(k), ... , рn(k) после любого (k-го) шага. Они находятся с помощью следующих рекуррентных соотношений:
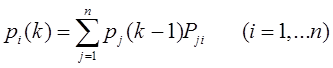 (4)
(4)
или в матричной форме
![]() (5)
(5)
где
![]() ,
, ![]() -
матрицы-строки вероятностей
состояний после k-го и (k-1)-го шагов соответственно;
-
матрицы-строки вероятностей
состояний после k-го и (k-1)-го шагов соответственно;
![]() - матрица переходных вероятностей.
- матрица переходных вероятностей.
Предположим, что в начальный момент (перед первым шагом) система находится в каком-то определенном состоянии, например Sm. Тогда для начального момента (0) будем иметь:
р1(0) =0, р2(0) =0, ..., рm(0) = 1, ... , рn(0) = 0 ,
т. е. вероятности всех состояний равны нулю, кроме вероятности начального состояния Sm, равной единице.
Найдем вероятности состояний после первого шага. Мы знаем, что перед первым шагом система заведомо находится в состоянии Sm. Значит, за первый шаг она перейдет в состояния S1, S2, ... , Sm, ... , Sn с вероятностями
Pm1, Pm2, ... , Pmm, ... , Pmn ,
находящимися в m-ой строке матрицы переходных вероятностей.
Таким образом, вероятности состояний после первого шага будут:
![]() (6)
(6)
Найдем вероятности состояний после второго шага:
![]() .
.
Вычислим их по формуле полной вероятности с гипотезами:
· после первого шага система была в состоянии S1;
· после первого шага система была в состоянии S2;
· после первого шага система была в состоянии Si;
· после первого шага система была в состоянии Sn.
Вероятности гипотез известны (6), условные вероятности перехода в состояние Si - при каждой гипотезе тоже известны и записаны в матрице переходных вероятностей. По формуле полной вероятности получим:
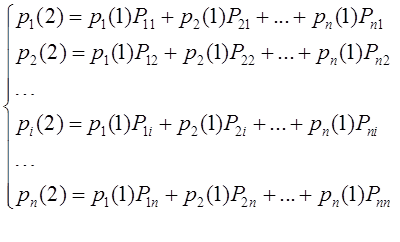 (7)
(7)
или
Данное выражение может быть записано в векторно-матричной форме:
![]() (9)
(9)
В формулах (7) –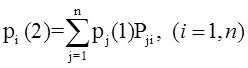 (8) суммирование распространяется формально на все состояния S1, S2, ... , Sm, ... , Sn ; фактически учитывать надо только те из них, для которых переходные
вероятности Pij отличны от нуля, т.е. те состояния, из которых может совершиться
переход в состояние Sl (или задержка в
нем).
(8) суммирование распространяется формально на все состояния S1, S2, ... , Sm, ... , Sn ; фактически учитывать надо только те из них, для которых переходные
вероятности Pij отличны от нуля, т.е. те состояния, из которых может совершиться
переход в состояние Sl (или задержка в
нем).
Таким образом, вероятности состояний после второго шага известны. Очевидно, после третьего шага они определяются аналогично:
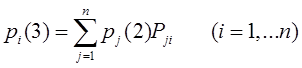 (10)
(10)
И вообще после k-то шага:
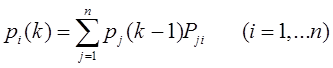 (11)
(11)
Таким образом, вероятности ![]() состояний после k-го шага
определяются рекуррентной формулой
состояний после k-го шага
определяются рекуррентной формулой ![]() (12) через вероятности состояний после (к -
1)-го шага; последние, в свою очередь, — через вероятности состояний после (к
- 2)-го шага, и т. д.
(12) через вероятности состояний после (к -
1)-го шага; последние, в свою очередь, — через вероятности состояний после (к
- 2)-го шага, и т. д.
Например, пусть требуется найти вероятность перехода системы из состояния S1 в состояние S2 за 3 шага для графа на рис. 9.
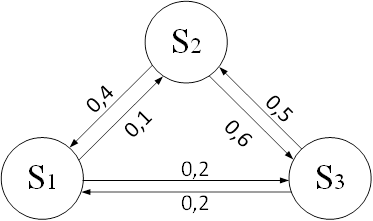
Рис. 9. Пример ГСП
Из
условия следует, что ![]() .
Находим вероятности состояния после первого шага:
.
Находим вероятности состояния после первого шага:
![]()
![]()
![]()
Вероятности состояния после второго шага:
![]()
![]()
![]()
Вероятность состояния S2 после
третьего шага ![]() :
:
![]()
Если обозначить через ![]() матрицу,
элементами которой являются вероятности переходов из Si в Sj за m шагов
матрицу,
элементами которой являются вероятности переходов из Si в Sj за m шагов ![]() ,
то справедлива формула:
,
то справедлива формула:
![]() , (13)
, (13)
где
матрица![]() получается умножением
матрицы P саму на себя m раз.
получается умножением
матрицы P саму на себя m раз.
Пусть исходное состояние системы задается вектором ![]() :
:
![]()
где
pi, i=1, … n есть вероятность того, что в начальный момент система находится в состоянии Si.
Тогда для нахождения вектора вероятностей состояния системы после m шагов можно воспользоваться формулой:
Воспользуемся приведенными формулами для нахождения вектора
состояния системы, изображенной рис. 9, после двух шагов, для случая, когда
исходное состояние системы задается вектором ![]() .
.
С помощью формулы ![]() (12) находим сначала состояние системы после первого шага
(12) находим сначала состояние системы после первого шага ![]() :
:
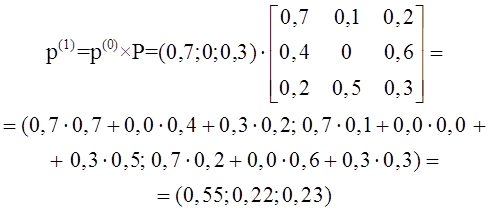
и состояние системы после второго шага ![]() :
:
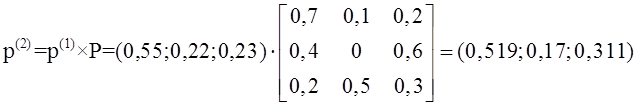
Тот же результат получается с помощью формулы ![]() (14). Вычислив предварительно величину
элементов матрицы
(14). Вычислив предварительно величину
элементов матрицы
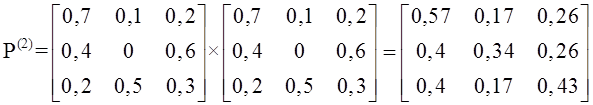
находим:
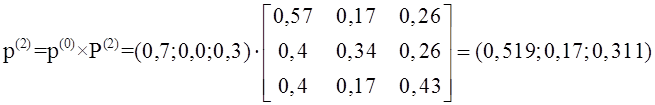
Матрицы, суммы элементов всех строк которых равны единице, называются стохастическими. Если при некотором n все элементы матрицы Р не равны нулю, то такая матрица переходов называется регулярной. Другими словами, регулярные матрицы переходов задают цепь Маркова, в которой каждое состояние может быть достигнуто через n шагов из любого состояния. Такие цепи Маркова так же называются регулярными.
Известно (теорема о предельных вероятностях), что для регулярной цепи Маркова с n состояниями и матрицей вероятностей перехода Р существует предел
![]()
и матрица ![]() имеет вид:
имеет вид:
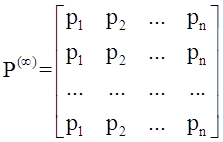
т.е. состоит из одинаковых строк.
Величины p1, p2, … , pn называются предельными вероятностями. Эти вероятности не зависят от исходного состояния системы, и вектор вероятности полностью определяется из условий:
![]() (или
(или 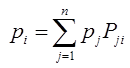 )
)
и условия нормировки
![]()
Пусть требуется найти предельные вероятности для матрицы переходов
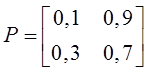
Так как ![]() , то, перемножив матрицы и приравняв строки,
получаем:
, то, перемножив матрицы и приравняв строки,
получаем:
![]()
![]()
![]()
![]()
![]()
и матрица предельных вероятностей:
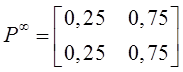
1. Решение многих задач, связанных с анализом процессов и создания систем, основано на рассмотрении протекающих процессов как стохастических. Для оценивания показателей этих процессов и систем применяются аналитические модели.
2. Важным классом случайных процессов является марковский процесс. Марковские процессы протекают в отсутствие предыстории, что значительно упрощает их математическое описание.
3. Для описания процесса с дискретным временем и дискретными состояниями используются граф переходов и состояний, а также связанная с ним матрица переходных вероятностей. На основе этих элементов можно найти вероятности нахождения процесса в каждом из своих состояний после любого шага, для чего применяются рекуррентные или матричные выражения, которые получены на основе формулы полной вероятности.
4. В случае регулярных цепей Маркова процесс обладает предельными вероятностями нахождения в каждом из своих состояний. Эти вероятности не зависят от номера шага и могут быть найдены путем решения системы линейных уравнений, получаемой из выражения для предельных вероятностей и нормировочного условия.
1. Что такое стохастическая система?
2. Какой процесс называется марковским?
3. Как классифицируются марковские процессы?
4. Дайте определение марковского процесса с непрерывным временем и дискретными состояниями.
5. Что такое однородный марковский процесс?
6. Что такое граф состояний и переходов (ГСП) Марковской цепи? Какие бывают ГСП?
7. Что понимается под матрицей переходных вероятностей?
8. Как можно найти вероятность нахождения процесса в определенном состоянии после определенного числа шагов?
9. Что такое нестационарная марковская цепь?
10. Что такое предельные вероятности марковского процесса?
11. Каков физический смысл предельных вероятностей?
12. При каких условиях существуют предельные вероятности состояний марковского процесса?
13. Как найти предельные вероятности системы, имеющей стационарный режим?
1. Емельянов А.А., Власова Е.А., Дума Р.В. Имитационное моделирование экономических процессов / Под ред. А.А. Емельянова. – М.: Финансы и статистика, 2009. – 480 с.
2. Теория систем и системный анализ в управлении организациями: Справочник / Под ред. В.Н. Волковой и А.А. Емельянова. – М.: Финансы.
3. Саати Т.Л. Элементы теории массового обслуживания и её приложения. – М.: Радио и связь, 1965. – 512 с.
· познакомиться с математическим аппаратом аналитического моделирования непрерывных марковских процессов;
· изучить математический аппарат описания марковских процессов;
· научиться находить характеристики процесса с помощью уравнений Колмогорова.
получите представление о:
· как построить математическую модель непрерывного марковского процесса;
· что такое стационарный режим и предельные вероятности;
· как найти вероятности нахождения марковского процесса в своих состояниях;
· что такое процесс гибели и размножения и как он используется для моделирования практических задач.
будете знать:
· как описать непрерывно протекающие процессы с помощью графа состояний и переходов;
· что такое интенсивности перехода процесса;
· как составить уравнения Колмогорова по графу состояний и переходов;
· как применить аппарат теории марковских процессов к практическим задачам построения систем.
1. Описание непрерывных цепей Маркова.
2. Уравнения Колмогорова.
3. Процессы гибели и размножения.
Рассмотрим пример. Пусть имеем систему S, включающую один компьютер, который может находиться в одном из пяти возможных состояний:
S1 — исправен, работает;
S2 — неисправен, ожидает осмотра;
S3 — осматривается;
S4 — ремонтируется;
S5 — списан.
ГСП системы показан на рис. 10.
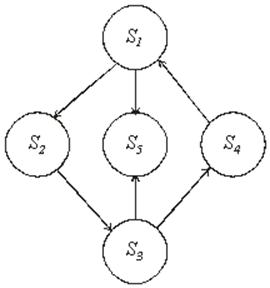
Рис. 10. Граф состояний и переходов процесса поломок и восстановлений
В примере на рис. 10 выход из строя
(отказ) компьютера и окончание его ремонта (восстановление) могут произойти в
заранее неизвестный момент. Для описания таких процессов может быть применена
схема марковского случайного процесса с дискретными состояниями и непрерывным
временем. Процессы такого типа известны как непрерывные цепи Маркова. Непрерывной
цепью Маркова (марковским процессом) называется процесс, для которого при ![]() выполняется:
выполняется:
![]()
Здесь рассматривается ряд дискретных состояний: S1, S2, S3, ..., Sn, однако переход системы S из состояния в состояние может происходить в произвольный момент времени.
Обозначим через pi(t) вероятность того, что в момент t система S будет находиться в состоянии Si (i= 1, ... , n). Очевидно, для любого момента t сумма вероятностей состояний равна единице:
Так как события, состоящие в том, что в момент t система находится в состояниях S1, S2 , ..., Sn , несовместны.
Необходимо определить для любого t вероятности состояний:
Для того чтобы найти эти вероятности, необходимо знать характеристики процесса. Поскольку вероятность перехода системы из состояния в состояние точно в момент t будет равна нулю (так же как вероятность любого отдельного значения непрерывной случайной величины), то в качестве характеристик процесса рассматриваются плотности вероятностей, или интенсивности перехода λij из состояния Si в состояние Sj.
Пусть система S в момент t находится в состоянии Sr. Рассмотрим элементарный промежуток времени Δt, примыкающий к моменту t. Назовем плотностью вероятности перехода λij из состояния i в состояние j предел отношения вероятности перехода системы за время Δt из состояния Si в состояние Sj к длине промежутка Δt:
где
Pij(Δt) — вероятность того, что система, находившаяся в момент t в состоянии Si за время Δt перейдет из него в состояние Sj (плотность вероятностей перехода определяется только для j≠i).
Из (3) следует, что при малом Δt вероятность перехода (с точностью до бесконечно малых высших порядков) равна:
Pij(Δt)=λij Δt
Если все плотности вероятностей перехода λij не зависят от t (от того, в какой момент начинается элементарный участок Δt)
![]() ,
,
то марковский процесс называется однородным, в противном случае - неоднородным.
Предположим, что известны плотности вероятностей перехода λij для всех пар состояний Si,Sj. ГСП системы с проставленными у стрелок плотностями вероятностей перехода называется размеченным графом состояний (рис. 11), на основании которого можно определить вероятности состояний рi(t) как функции времени (2) .
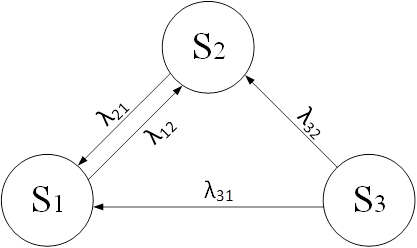
Рис. 11. Пример размеченного графа состояний и переходов
Если протекающий в системе случайный
процесс является марковским процессом с непрерывным временем, то для
вероятностей ![]() можно составить систему линейных
дифференциальных уравнений, называемых уравнениями Колмогорова. Покажем,
как получаются эти уравнения на примере ГСП рис 11.
можно составить систему линейных
дифференциальных уравнений, называемых уравнениями Колмогорова. Покажем,
как получаются эти уравнения на примере ГСП рис 11.
Рассмотрим вначале вершину графа ![]() . Вероятность
. Вероятность ![]() того,
что система в момент времени (t + Δt) окажется в состоянии
того,
что система в момент времени (t + Δt) окажется в состоянии ![]() , определяется на основе рассмотрения
трех возможностей попасть в это состояние:
, определяется на основе рассмотрения
трех возможностей попасть в это состояние:
1)
Система в момент
времени t с вероятностью ![]() находилась
в состоянии
находилась
в состоянии ![]() и за малое время
Δt не перешла в состояние
и за малое время
Δt не перешла в состояние![]() . Из
состояния
. Из
состояния ![]() система может быть выведена
потоком интенсивностью
система может быть выведена
потоком интенсивностью![]() . Вероятность
выхода системы из состояния
. Вероятность
выхода системы из состояния ![]() за время
Δt с точностью до величин более высокого порядка малости по Δt
равна
за время
Δt с точностью до величин более высокого порядка малости по Δt
равна ![]() , а вероятность сохранения состояния
, а вероятность сохранения состояния
![]() будет равна
будет равна ![]() .
.
При этом вероятность того, что система останется в состоянии ![]() , согласно теореме об умножении
вероятностей будет равна
, согласно теореме об умножении
вероятностей будет равна![]() .
.
2)
Система в момент
времени t находилась в состоянии ![]() и
за время Δt под воздействием потока
и
за время Δt под воздействием потока![]() перешла
в состояние
перешла
в состояние ![]() с вероятностью
с вероятностью ![]() . Вероятность того, что система будет
находиться в состоянии
. Вероятность того, что система будет
находиться в состоянии ![]() , равна
, равна![]() .
.
3)
Система в момент
времени t находилась в состоянии ![]() и
за время Δt под воздействием потока
и
за время Δt под воздействием потока ![]() перешла в состояние
перешла в состояние ![]() с цвероятностью
с цвероятностью ![]() . Вероятность того, что система
будет находиться в состоянии
. Вероятность того, что система
будет находиться в состоянии ![]() , равна
, равна![]() .
.
По теореме сложения вероятностей получим:
![]()
![]()
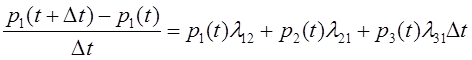
и, переходя к пределу Δt → 0,
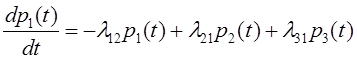
Аналогично, рассматривая вершины графа ![]() и
и
![]() , получим уравнения
, получим уравнения
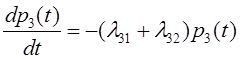
К этим уравнениям необходимо добавить нормировочное условие, которое в данном случае имеет вид
![]()
Решение этой системы уравнений в зависимости от времени можно найти либо аналитически, либо численно с учетом начальных условий.
На основе рассмотренного примера можно сформулировать общее правило составления уравнений Колмогорова:
В левой части каждого уравнения стоит производная вероятности какого-то (j-го) состояния. В правой части - сумма произведений вероятностей всех состояний, из которых идут стрелки в данное состояние, на интенсивности соответствующих потоков, минус суммарная интенсивность всех потоков, выводящих систему из данного (j-го) состояния, умноженная на вероятность данного (j-го) состояния.
Это правило составления дифференциальных уравнений для вероятностей состояний является универсальным и применимо к любому марковскому процессу с непрерывным временем; с его помощью можно без проведения специального рассмотрения условий задачи, записывать дифференциальные уравнения для вероятностей состояний непосредственно по размеченному графу состояний.
Весьма важным является вопрос о том, что
будет происходить с системой при ![]() , а именно,
будут ли функции р(t), р2(t), ... , рn(t) стремиться к каким-то пределам. Эти
пределы, если они существуют, называются предельными (или финальными)
вероятностями состояний.
, а именно,
будут ли функции р(t), р2(t), ... , рn(t) стремиться к каким-то пределам. Эти
пределы, если они существуют, называются предельными (или финальными)
вероятностями состояний.
В самой системе S устанавливается некоторый предельный
стационарный режим: система хоть и меняет случайным образом свои состояния, но
вероятность каждого из них не зависит от времени и каждое из состояний
осуществляется с некоторой постоянной вероятностью, которая представляет собой среднее
относительное время пребывания системы в данном состоянии. Например, если у
системы три возможных состояния: ![]() ,
, ![]() и
и ![]() ,
причем их предельные вероятности равны 0,2; 0,3 и 0,5, то
это означает, что после перехода к установившемуся режиму система в среднем
20% времени будет находиться в состоянии
,
причем их предельные вероятности равны 0,2; 0,3 и 0,5, то
это означает, что после перехода к установившемуся режиму система в среднем
20% времени будет находиться в состоянии ![]() ,
30% — в состоянии
,
30% — в состоянии ![]() и 50% — в
состоянии
и 50% — в
состоянии ![]() .
.
Доказано, что если число состояний системы S конечно и из каждого состояния можно перейти (за то или иное число шагов) в любое другое, то предельные вероятности состояний существуют и не зависят от начального состояния системы. В этом случае в процессе моделирования системы можно ограничиваться для нахождения ее параметров одной достаточно длинной реализацией процесса.
Вычислить все предельные вероятности можно, перейдя от системы дифференциальных уравнений к системе линейных алгебраических уравнений, дополнив ее нормировочным условием.
Найдем финальные вероятности pj системы уравнений для ГСП на рис 11. Полагая dpi/dt = 0 (j=1,2, 3) получаем три алгебраических уравнения, которые являются однородными. Поэтому одно из них можно отбросить. Отбросим, например, второе уравнение и вместо него запишем нормировочное условие. В результате система уравнений для финальных вероятностей примет вид:
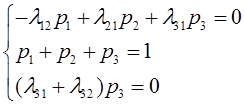
Из последнего уравнения следует, что
p3 = 0
Решая оставшиеся уравнения, получим
p1= 2/3,
p2 = 1/3
Т.е., вектор состояния системы в стационарном режиме равен
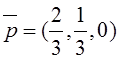
Как мы увидели, имея размеченный ГСП системы, можно сразу написать алгебраические уравнения для предельных вероятностей состояний. Таким образом, если две непрерывные цепи Маркова имеют одинаковые графы состояний и различаются только значениями интенсивностей λij, отсутствует необходимость находить предельные вероятности состояний для каждого из графов в отдельности, достаточно составить и решить уравнения для одного из них, а затем подставить вместо λij соответствующие значения. Для многих часто встречающихся на практике форм графов линейные уравнения без особых затруднений решаются в алгебраическом виде.
Рассмотрим практический пример. Пусть имеется система, состоящая из двух серверов, которая обрабатывает поток поступающих к ней запросов (рис. 12, а).
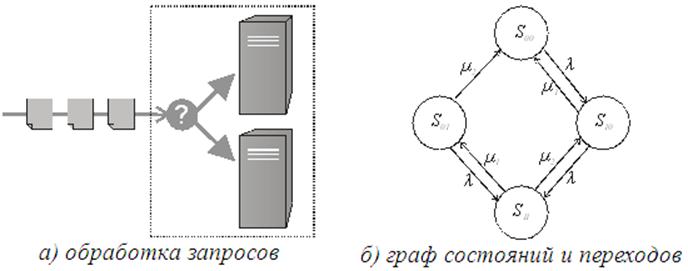
Рис. 12. Система с двумя серверами
Средний интервал между поступлениями
запросов ![]() , производительность серверов
неодинакова: среднее время обработки запроса первым сервером составляет
, производительность серверов
неодинакова: среднее время обработки запроса первым сервером составляет ![]() , второго –
, второго – ![]() ,
,
![]() .
.
Если в момент поступления в систему очередной заявки:
· первый сервер свободен, то заявка берется на обработку первым сервером;
· первый сервер занят обслуживанием, а второй сервер свободен, то заявка берется на обработку вторым сервером;
· оба сервера заняты обслуживанием, то заявка теряется.
В предположении экспоненциального характера
распределения ![]() ,
, ![]() ,
,
![]() требуется найти вероятность отказа в
обслуживании запроса
требуется найти вероятность отказа в
обслуживании запроса![]() .
.
В силу экспоненциального характера распределения временных параметров процесс можно считать марковским. Поэтому решение задачи начинаем с построения ГСП процесса.
Исследуемый процесс может находиться в следующих состояниях:
S00 – оба сервера свободны,
S10 – первый сервер занят, второй свободен,
S01 – первый сервер свободен, второй занят,
S11 – оба сервера заняты.
![]() -
интенсивность потока запросов к системе;
-
интенсивность потока запросов к системе;
![]() -
интенсивность обработки запросов первым сервером;
-
интенсивность обработки запросов первым сервером;
![]() -
интенсивность обработки запросов вторым сервером.
-
интенсивность обработки запросов вторым сервером.
то размеченный ГСП будет иметь вид, показанный на рис. 12, б.
Соответствующие уравнения Колмогорова для установившегося режима:
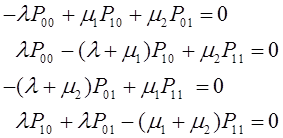
Вероятность отказа в обработке запроса
есть не что иное как вероятность ![]() занятости
обслуживанием обоих серверов. Оставив из имеющихся уравнений три и дополнив их
условием нормировки:
занятости
обслуживанием обоих серверов. Оставив из имеющихся уравнений три и дополнив их
условием нормировки:
![]()
решаем далее полученную систему линейных алгебраических уравнений (например, методом подстановки).
Важной разновидностью непрерывных марковских цепей является процесс гибели и размножения. Происхождение термин берет в биологии, где такая схема описывает процессы изменения численности популяции, распространения эпидемий и т.п.
Марковская непрерывная цепь называется процессом гибели и размножения, если ее ГСП имеет вид, представленный на рис. 13.

Рис. 13. Процесс гибели и размножения
Граф на рисунке
имеет вид цепочки, крайние звенья которой связаны переходами только с одним
соседним звеном, а каждое внутреннее связано прямой и обратной связью с каждым
из соседних. Величины ![]() (интенсивности
переходов системы из состояния в состояние слева направо) можно трактовать как
интенсивности рождения, величины
(интенсивности
переходов системы из состояния в состояние слева направо) можно трактовать как
интенсивности рождения, величины ![]() (интенсивности
переходов системы из состояния в состояние справа налево) - как интенсивности
гибели.
(интенсивности
переходов системы из состояния в состояние справа налево) - как интенсивности
гибели.
Запишем алгебраические уравнения для вероятностей состояний в установившемся режиме. Для каждого состояния поток, втекающий в данное состояние, должен равняться потоку, вытекающему из данного состояния.
Для состояния ![]() :
:
![]()
Для состояния ![]() :
:
![]()
С учетом равенства для состояния S1 равные друг другу члены справа и слева можно сократить, поэтому получаем:
![]()
Аналогично, для ![]() :
:
![]()
Вообще для состояния k, k = 2,..n, имеем:
![]()
Таким образом, предельные вероятности
состояний ![]() ,
,![]() ,
... ,
,
... ,![]() процесса размножения
и гибели можно найти из уравнений:
процесса размножения
и гибели можно найти из уравнений:
![]()
![]()
![]()
![]()
![]()
которые нужно дополнить нормировочным условием:
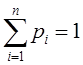
Последовательно выразим из каждого
уравнения переменные через ![]() .
.
Из первого уравнения выразим![]() :
:
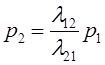
Из второго уравнения с учетом выражения
для ![]() выразим
выразим ![]() :
:
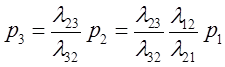
Вообще, для k , k = 2, ... n, имеем:
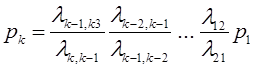
Подставив полученные выражения для ![]() ,
,![]() , ... ,
, ... ,![]() в
нормировочное условие и вынося
в
нормировочное условие и вынося ![]() , получаем:
, получаем:
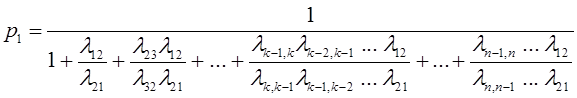
Остальные вероятности легко выражаются
через ![]() .
.
Как показано в
ряде работ, для существования стационарного режима необходимо и достаточно
необходимо и достаточно, чтобы ![]() .
.
Рассмотрим простой практический пример. Пусть небольшой компьютерный класс состоит из трех одинаковых компьютеров, каждый из которых может выходить из строя с интенсивностью l=1 компьютер/сутки. Отказавший компьютер немедленно начинает восстанавливаться, на восстановление уходят в среднем также одни сутки, m=1 сутки -1. Требуется найти вероятности числа неисправных компьютеров.
Определим возможные состояния системы:
![]() - все три компьютера исправны;
- все три компьютера исправны;
![]() - один компьютер восстанавливается, два исправны;
- один компьютер восстанавливается, два исправны;
![]() - два компьютера восстанавливаются, один исправен;
- два компьютера восстанавливаются, один исправен;
![]() - все три компьютера
восстанавливаются.
- все три компьютера
восстанавливаются.
Размеченный ГСП системы показан на рис. 14.
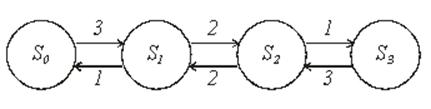
Рис. 14. Процесс поломок и восстановлений компьютерного класса
Из графа видно, что
процесс, протекающий в системе, представляет собой процесс гибели и
размножения. Значения интенсивностей переходов для состояния с номером k определяются
так: интенсивность перехода в состояние с большим номером равна ![]() , поскольку интенсивность поломок кратна
числу исправных компьютеров
, поскольку интенсивность поломок кратна
числу исправных компьютеров ![]() ; интенсивность
перехода в состояние с меньшим номером равна
; интенсивность
перехода в состояние с меньшим номером равна![]() ,
поскольку интенсивность восстановления кратна числу неисправных компьютеров
,
поскольку интенсивность восстановления кратна числу неисправных компьютеров ![]() .
.
Используя выражения для вероятностей состояний процесса гибели и размножения, получаем:
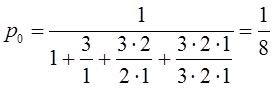
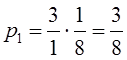
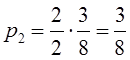
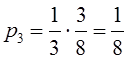
Выводы:
1. В ряде практически важных случаев протекающие в системах процессы могут быть описаны как марковские процессы с дискретным множеством состояний и непрерывным временем. Это позволяет применить для их математического описания аппарат дифференциальных уравнений Колмогорова, с помощью которых можно получить числовые характеристики процессов.
2. Особый интерес во многих прикладных задачах представляет стационарный режим, в который по истечении некоторого времени входит марковский процесс. Если такой режим существует, то предельные вероятности находятся путем решения системы алгебраических линейных уравнений, получаемых из уравнений Колмогорова дополненных нормировочным условием.
3. Важным частным случаем марковских процессов с непрерывным временем являются процессы гибели и размножения. Их обобщенное решение, получаемое на основе уравнений Колмогорова, позволяет решать целый класс практических задач и строить модели многих систем, в частности, систем массового обслуживания, которые будут рассматриваться в следующей теме.
1. Дайте определение марковского процесса с непрерывным временем и дискретными состояниями?
2. Как описывается марковского процесса с непрерывным временем и дискретными состояниями?
3. Что такое интенсивность перехода?
4. Что такое установившийся режим?
5. Каким правилом можно пользоваться для записей уравнений Колмогорова?
6. Что такое предельные вероятности марковского процесса?
7. При каких условиях существуют предельные вероятности состояний марковского процесса?
8. Каков физический смысл предельных вероятностей?
9. Как найти предельные вероятности системы, имеющей стационарный режим?
10. Что называется процессами гибели и размножения? Поясните на ГСП.
11. Запишите выражения для предельных вероятностей процесса гибели и размножения.
12. Приведите практические примеры процессов, описываемых как марковские процессы с непрерывным временем и дискретными состояниями.
1. Емельянов А.А., Власова Е.А., Дума Р.В., Емельянова Н.З. Компьютерная имитация экономических процессов: Учебник / Под ред. А.А. Емельянова. – М.: Маркет ДС, 2010. – 464 с.
2. Саати Т.Л. Элементы теории массового обслуживания и её приложения. – М.: Радио и связь, 1965. – 512 с.
3. Климов Г.П. Теория массового обслуживания. – М.: Издательство МГУ, 2011. – 312 с.
· познакомиться с основными аналитическими моделями систем массового обслуживания.
· научиться применять математический аппарат описания марковских процессов к построению моделей систем массового обслуживания;
· познакомиться с основными показателями, используемыми в моделях систем массового обслуживания.
получите представление о:
· как строятся математические модели систем массового обслуживания на примере системы с отказами;
· как применяются модели систем массового обслуживания;
будете знать:
· как характеризуется пропускная способность систем с отказами и как они рассчитываются;
· какие показатели характеризуют очередь в системе с ожиданием и как они рассчитываются;
· как применить модели к решению экономических и инженерных задач.
1. Система массового обслуживания.
2. Моделирование одноканальной СМО с отказами.
3. Оптимизация показателей многоканальной СМО с отказами.
4. Обслуживание с очередями.
5. Многоканальная СМО сограниченной очередью.
Значительный интерес для практики представляют модели систем массового обслуживания (СМО), к которым сводятся множество задач анализа и проектирования информационных систем. Системы этого класса характеризуются наличием (рис. 15) потока запросов (заявок), поступающих на вход системы (входящим потоком), необязательной очереди ждущих обслуживания заявок, обслуживающим прибором, или каналом и потоком обслуженных заявок (выходящим потоком).
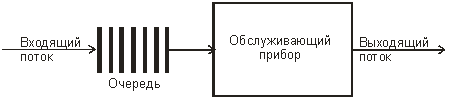
Рис. 15. Элементы СМО
Поток заявок (другие названия: запросы, вызовы, требования и т.д.), исходящий из источника заявок, поступает на вход СМО в случайные моменты времени для обслуживания. Этот входной поток может представлять собой вызовы от абонентов, передаваемые сообщения и т.д. Обслуживание поступившей заявки продолжается некоторое случайное время, после чего канал освобождается и готов к принятию следующей заявки. Случайный характер потока заявок приводит к тому, что в какие-то промежутки времени на входе СМО скапливается излишне большое число заявок (они либо образуют очередь, либо покидают СМО не обслуженными); в другие же периоды СМО будет работать с недогрузкой или простаивать.
Для СМО в рамках теории массового обслуживания разработаны математические модели, которые широко применяются для количественного оценивания системных показателей. Многие модели основаны на уже рассмотренном ранее аппарате марковских процессов. Проиллюстрируем применение теории на нескольких моделях СМО.
Примером одноканальной СМО с отказами, которая является простейшей из моделей, может служить телефонное справочное бюро. В случае незанятой линии происходит соединение с оператором, и абонент получает ответ на заданный вопрос, в противном случае соединение не устанавливается и звонок необходимо повторить. Считая интервалы между звонками и продолжительность разговора случайными величинами, распределенными по экспоненциальному закону, процесс в такой системе можно рассматривать как марковский. Обозначив через l интенсивность входящего потока, m - интенсивность обслуживания, можно построить размеченный ГСП (рис. 16Рис.) .
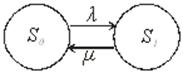
Рис. 16. ГСП одноканальной СМО с отказами
Вероятности состояний системы ![]() (вероятность того, что в системе находится 0 заявок) и
(вероятность того, что в системе находится 0 заявок) и ![]() (вероятность того, что в
системе находится 1 заявка) для стационарного режима определяются из выражений
для вероятностей состояний процесса гибели и
размножения, который был рассмотрен в предшествующей теме:
(вероятность того, что в
системе находится 1 заявка) для стационарного режима определяются из выражений
для вероятностей состояний процесса гибели и
размножения, который был рассмотрен в предшествующей теме:
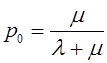
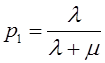
Из этих выражений можно
определить показатели одноканальной СМО. В частности, вероятность отказа
в обслуживании ![]() :
:
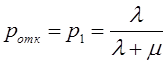 (1)
(1)
поскольку запрос получает
отказ в случае, когда обслуживающий прибор занят, и относительную пропускную
способность ![]() , которая представляет собой
отношение среднего числа обслуженных заявок за единицу
времени к среднему числу всех поступивших заявок за тоже время:
, которая представляет собой
отношение среднего числа обслуженных заявок за единицу
времени к среднему числу всех поступивших заявок за тоже время:
Поскольку![]() есть вероятность
того, что в момент t
канал свободен, или
вероятность того, что заявка, пришедшая в момент t, будет
обслужена.
есть вероятность
того, что в момент t
канал свободен, или
вероятность того, что заявка, пришедшая в момент t, будет
обслужена.
Зная q легко найти абсолютную пропускная способность А, которая определяется как среднее число заявок, которое может обслужить СМО в единицу времени. Эти показатели связаны очевидным соотношением
В
многоканальной СМО имеется n
каналов обслуживания, которые функционируют независимо друг от друга. Очередь отсутствует, т.е., заявки, заставшие все каналы занятыми
обслуживанием, получают отказ, и уходят из системы. Входной поток заявок
и поток обслуживания заявок являются пуассоновскими. Интенсивность поступления
заявок равна ![]() , интенсивность обслуживания
, интенсивность обслуживания ![]() .
.
СМО может находиться в следующих состояниях:
· S0 - в СМО 0 заявок (все каналы свободны);
· S1 - в СМО 1 заявка (один канал занят, остальные свободны);
· Sk - в СМО n заявок (k каналов заняты, остальные свободны);
· Sn - в СМО n заявок (все каналы заняты).

Рис. 171. ГСП многоканальной СМО с отказами
Если система находится в состоянии S1, то поток, переводящий систему в состояние S0, будет иметь интенсивность μ.
Если система находится в состоянии S2, то поток, переводящий систему в состояние S1, будет иметь интенсивность 2μ. (два канала порождают поток с интенсивностью в два раза большей).
Если система находится в состоянии Sk, то поток, переводящий систему в состояние Sk-1, будет иметь интенсивность kμ. (k каналов порождают поток с интенсивностью в k раз большей).
Процесс, показанный на рис. 17, представляет собой частный случай процесса гибели и размножения.
Уравнения Колмогорова для вероятностей состояний системы P0 , P1 , ... , Pn будут иметь следующий вид:
Предельные вероятности имеют вид
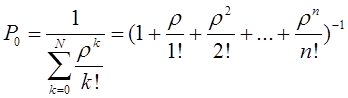
где 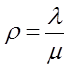 .
.
Соотношения 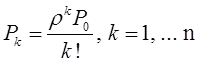 (5)
называются формулами Эрланга. С их помощью можно найти предельные
вероятности в зависимости от значений параметров λ и μ.
Характеристики стационарного режима таковы.
(5)
называются формулами Эрланга. С их помощью можно найти предельные
вероятности в зависимости от значений параметров λ и μ.
Характеристики стационарного режима таковы.
Вероятность отказа. Заявка получает отказ, если все каналы заняты. Вероятность этого равна:
Относительная пропускная
способность есть вероятность того,
что заявка будет принята к обслуживанию и может быть найдена как
дополнение ![]() до 1:
до 1:
Абсолютная пропускная способность находится как
Среднее число заявок в системе (среднее число занятых каналов) можно вычислить через вероятности P0, P1, …, Pk,… Pn, по формуле
![]() (9)
(9)
как математическое ожидание
дискретной случайной величины. Однако, проще выразить среднее число занятых
каналов через абсолютную пропускную способность А, которая уже известна.
Действительно, А есть среднее число заявок, обслуживаемых в единицу
времени; один занятый канал обслуживает в среднем μ заявок в
единицу времени; среднее число занятых каналов получается делением А на ![]()
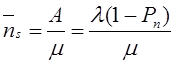
или, переходя к обозначению
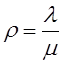 :
:
![]()
Посмотрим, как может применяться описанная модель для решения оптимизационной задачи проектирования системы. Пускай нам требуется определить наиболее предпочтительный (в смысле экономического эффекта) вариант многоканальной СМО с отказами. Для этого необходимо определить число обслуживающих приборов n, при котором достигается максимум функции
где
![]() – величина
получаемой прибыли;
– величина
получаемой прибыли;
![]() – получаемый
в результате эксплуатации системы доход;
– получаемый
в результате эксплуатации системы доход;
![]() – стоимость
эксплуатации приборов (все величины приведены к единице времени).
– стоимость
эксплуатации приборов (все величины приведены к единице времени).
Будем искать решение при таких предположениях:
·
средний интервал времени между
заявками в потоке (![]() ) составляет 5 мин;
) составляет 5 мин;
·
заявка обрабатывается в среднем 5
мин (![]() );
);
·
затраты на эксплуатацию одного
прибора (![]() ) составляют 1 рублей/мин;
) составляют 1 рублей/мин;
·
доход от одной обслуженной заявки (![]() ) равен 80 рублей.
) равен 80 рублей.
Значение функции ![]() находится как произведение величины
абсолютной пропускной способности на величину дохода от обслуживания одной
заявки:
находится как произведение величины
абсолютной пропускной способности на величину дохода от обслуживания одной
заявки:
![]()
Значение функции ![]() находится как произведение затрат на
эксплуатацию одного прибора на число приборов:
находится как произведение затрат на
эксплуатацию одного прибора на число приборов:
![]()
Поэтому,
подставляя в ![]() (10), получаем
(10), получаем
Сначала определим значение ![]() :
:
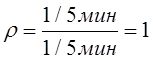
Далее по формуле ![]() (3) находим величину абсолютной пропускной способности для нескольких
значений n:
(3) находим величину абсолютной пропускной способности для нескольких
значений n:
n=1:
По
формуле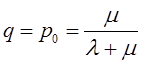 (2) находим q
(2) находим q
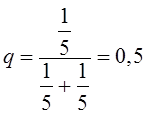
и по формуле ![]() (3)
(3)
![]()
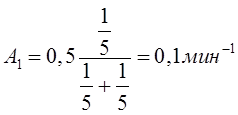
n=2:
По
формулам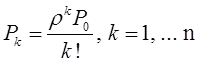 (5)
находим сначала
(5)
находим сначала![]()
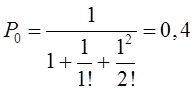
затем по формуле (6) ![]()
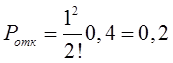
и по формуле ![]() (8)
(8) ![]()
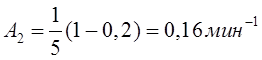
Аналогично получаем:
n=3:
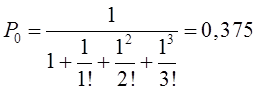
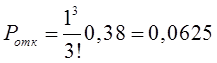
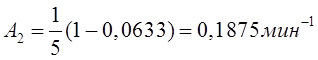
n=4:
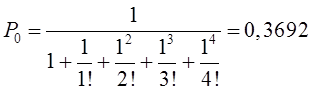
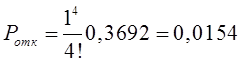
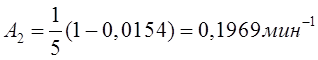
n=5:
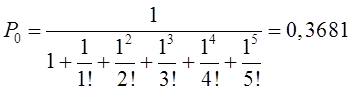
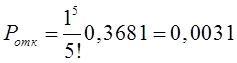
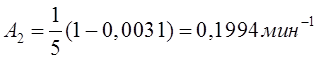
Подставляя найденные
значения в ![]() (11) находим:
(11) находим:
![]()
![]()
![]()
![]()
![]()
График зависимости P от n имеет вид:
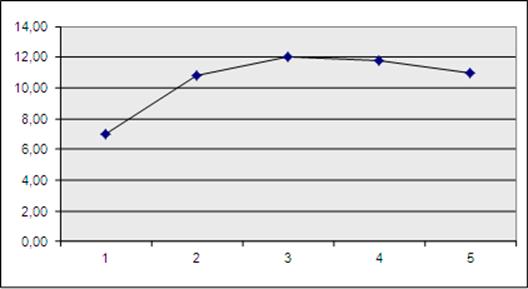
Рис. 18. Зависимость величины приведенной прибыли от числа приборов
Как видим, максимум прибыли в единицу времени достигается для числа обслуживающих приборов равного трем.
В системах с ожиданием заявки, заставшие обслуживающий прибор в момент прихода занятым, в отличие от систем с отказами не покидают систему, а остаются ждать в очереди вместе с другими ждущими заявками (рис. 15).
Для описания таких систем
используются показатели, характеризующие длину очереди и время ожидания
заявками обслуживания. В частности, если временной интервал между появлением
заявок распределен по экспоненциальному закону (пуассоновский поток), то среднее
время ожидания заявки в очереди ![]() можно найти по формуле
Хинчина-Полачека:
можно найти по формуле
Хинчина-Полачека:
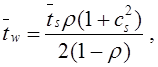 (12)
(12)
где
![]() —
среднее время обслуживания заявки;
—
среднее время обслуживания заявки;
σs — среднеквадратическое (стандартное) отклонение времени обслуживания в приборе;
ρ —
коэффициент использования прибора 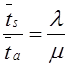 ;
;
![]() — средний интервал времени между
поступлением заявок;
— средний интервал времени между
поступлением заявок;
cs —
коэффициент вариации времени обслуживания ![]() .
.
Число заявок,
ожидающих обслуживания (среднюю длина очереди), можно найти, умножив ![]() на величину λ:
на величину λ:
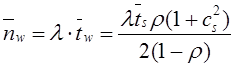 (13)
(13)
что, с учетом равенства
![]()
дает
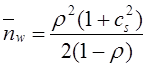 (14)
(14)
Формула Хинчина-Полачека используется для оценивания длин очередей при проектировании информационных систем. Она применяется в случае экспоненциального распределения времени поступления при любом распределении времени обслуживания и любой дисциплине управления, лишь бы выбор очередного сообщения для обслуживания не зависел от времени обслуживания.
При проектировании систем встречаются такие ситуации возникновения очередей, когда дисциплина обслуживания выбирается в зависимости от времени обслуживания. Например, в некоторых случаях для первоочередного обслуживания могут выбираться более короткие сообщения с тем, чтобы получить меньшее среднее время обслуживания (среднее время пребывания в заявки системе). При управлении линией связи (каналом Интернет) можно присвоить входным сообщениям более высокий приоритет, чем выходным, поскольку первые короче. В таких случаях уже необходимо использовать не уравнение Хинчина — Поллачека или производные от него, а более сложные уравнения или использовать метод имитационного моделирования, рассматриваемы далее.
Особый интерес для практических применений представляют два случая.
1) Время обслуживания постоянно.
При
регулярном характере потока рассеяние отсутствует, поэтому среднеквадратическое отклонение ![]() ,
и формулы (12), (13) преобразуются в выражения
,
и формулы (12), (13) преобразуются в выражения
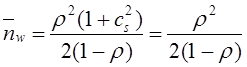 (15)
(15)
и
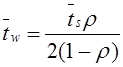 (16)
(16)
2) Время обслуживания имеет экспоненциальное распределение.
В
случае экспоненциального распределения, как известно, среднеквадратическое
отклонение ![]() , поэтому (12), (13) принимают вид:
, поэтому (12), (13) принимают вид:
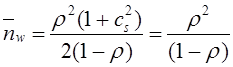 (17)
(17)
и
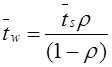 (18)
(18)
Большинство значений времени обслуживания в информационных системах лежит где-то между этими двумя значениями. Времена обслуживания, равные постоянной величине, встречаются редко. Даже время доступа к твердому диску непостоянно из-за различного положения массивов с данными на поверхности. Одним из примеров, иллюстрирующих случай постоянного времени обслуживания может служить занятие линии связи для передачи сообщений фиксированной длины.
С другой стороны, разброс времени обслуживания обычно не так
велик, как в случае произвольного или экспоненциального распределения, т.е., ![]() редко достигает значений
редко достигает значений ![]() . Этот случай иногда считают наихудшим
и потому пользуются формулами, относящимися к экспоненциальному распределению
времени обслуживания. Такой расчет может дать несколько завышенные размеры
очередей и времен ожидания в них, но эта ошибка, по крайней мере, не опасна.
. Этот случай иногда считают наихудшим
и потому пользуются формулами, относящимися к экспоненциальному распределению
времени обслуживания. Такой расчет может дать несколько завышенные размеры
очередей и времен ожидания в них, но эта ошибка, по крайней мере, не опасна.
Экспоненциальное распределение времен обслуживания не наихудший случай, с которым приходится иметь дело в действительности. Однако, если времена обслуживания, полученные при расчете очередей, оказываются распределенными хуже, чем времена с экспоненциальным распределением, то его можно рассматривать как предостережение разработчику. Если стандартное отклонение больше среднего значения, то обычно возникает необходимость в коррекции расчетов.
Покажем, каким образом можно использовать формулу (13) для улучшения характеристик СМО. Пусть имеются шесть типов сообщений, требующих для своего обслуживания соответственно 15, 20, 25, 30, 35, 40 и 300 временных единиц. Число сообщений каждого типа одинаково. Стандартное отклонение указанных времен несколько выше их среднего. Значение последнего времени обслуживания намного больше других. Это приведет к тому, что сообщения будут находиться в очереди значительно дольше, чем, если бы времена обслуживания были одного порядка. В таком случае при проектировании целесообразно принять меры для уменьшения длины очереди. Например, если указанные значения связаны с длинами приходящих сообщений, то, возможно, очень длинные сообщения стоит разделить на части.
Получим количественную оценку системных показателей для первоначального варианта организации информационного обмена и для двух вариантов, в которых длины сообщений передаваемых сообщений выровнены.
Вычислим величины, входящие в формулу для средней длины очереди. Будем считать, что средняя продолжительность для всей группы сообщений составляет 600 временных единиц. Тогда коэффициент загрузки
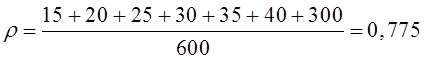
математическое ожидание времени обслуживания
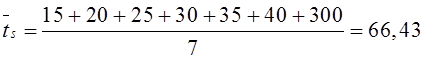
среднеквадратическое отклонение времени обслуживания
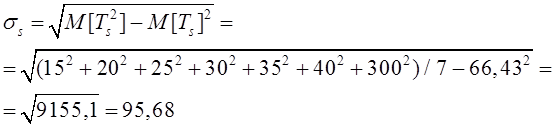
коэффициент вариации времени обслуживания
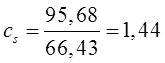
Подставляя в (13) получаем средний размер очереди в первоначальном варианте:
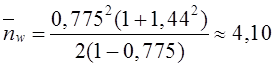
Вычислим теперь этот показатель для случая, когда последнее сообщение разбивается на два сообщения одинаковой длины. Поступая аналогичным образом, будем иметь (очевидно, что значение ρ остается тем же):
![]()
![]()
![]()
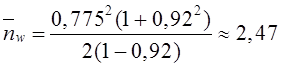
Разбивая длинное сообщение теперь уже на три части, получаем для средней длины очереди значение
![]()
Видим, что прибегая к разбиению длинного сообщения на три сообщения одинаковой длины можно сократить среднюю длину образующейся в системе очереди более чем вдвое.
Помимо моделей теории массового обслуживания для решения задач, связанных с анализом и проектированием информационных систем, структура которых может рассматриваться как СМО, применяются также и имитационные модели, которые рассматриваются далее.
Входящий поток заявок на обслуживание - простейший поток с интенсивностью λ.
Интенсивность потока обслуживания равна μ. Длительность обслуживания – случайная величина, подчиненная показательному закону распределения. Поток обслуживаний является простейшим пуассоновским потоком событий. Размер очереди допускает нахождение в ней m заявок.
СМО может находиться в следующих состояниях:
· S0 - в СМО 0 заявок (все каналы свободны, очереди нет);
· S1 - в СМО 1 заявка (1 канал занят, очереди нет);
· S2 - в СМО 2 заявки (2 канала заняты, очереди нет);
· Sk - в СМО k заявок (k каналов заняты, очереди нет);
· Sn - в СМО n заявок (n каналов занято, очереди нет);
· Sn+1 - в СМО n+1 заявка (n каналов занято, 1 заявка в очереди);
· Sn+r - в СМО n+r заявок (n каналов занято, r заявок в очереди);
· Sn+m - в СМО n+ m заявок (n каналов занято, m заявок в очереди).
ГСП системы показан на рис. 19. ГСП многоканальной СМО с ограниченной очередью:
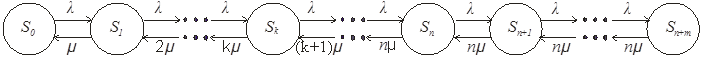
Рис. 19. ГСП многоканальной СМО с ограниченной очередью
ГСП есть схема процесса размножения и гибели, для него можно использовать общее решение для предельных вероятностей.
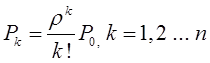
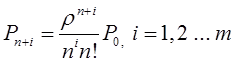
где 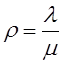 (использовано выражение для суммы
геометрической прогрессии со знаменателем
(использовано выражение для суммы
геометрической прогрессии со знаменателем ![]() ).
).
Вероятность отказа в обслуживании заявки.
Отказ произойдет в случае, если все n каналов заняты и в очереди находятся m заявок:
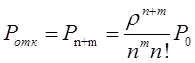 (20)
(20)
Относительная пропускная способность:
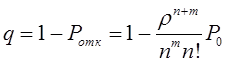
Абсолютная пропускная способность:
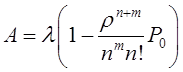
Среднее число занятых каналов.
Для СМО с очередью среднее число занятых каналов не совпадает - в отличие от СМО с отказами - со средним числом заявок в системе. Отличие равно числу заявок, ожидающих в очереди.
Каждый занятый канал обслуживает в среднем μ заявок в единицу времени, а СМО в целом – А заявок в единицу времени. Разделив А на μ получим
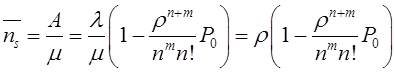
Среднее число находящихся в очереди заявок.
Найдем среднее число ожидающих в очереди заявок:
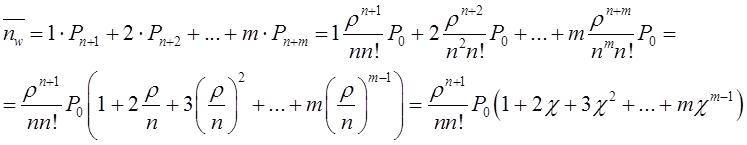 (21)
(21)
где ![]() =
=![]() .
.
Выражение в скобках можно трактовать (как и ранее) как производную по ρ от суммы геометрической прогрессии и получить выражение:
которым можно пользоваться
во всех случаях кроме ![]() =0.
=0.
Среднее число находящихся в системе заявок.
Поскольку
среднее число находящихся в системе заявок ![]()
![]()
Среднее время ожидания заявки в очереди.
Рассмотрим возможные ситуации, в которых пришедшая заявка может застать СМО.
Если заявка приходит в систему в какой-то момент времени и какой-то канал не занят, то она не будет ждать в очереди.
Если заявка приходит в систему в момент, когда заняты все каналы, а очереди нет, то она будет ждать в очереди в среднем 1/nμ (поток освобождения n каналов имеет интенсивность nμ).
Если заявка приходит в систему в момент, когда заняты все каналы, а в очереди одну заявку, то она будет ждать в очереди в среднем 2/nμ (по 1/nμ на каждую впередистоящую заявку).
Если заявка приходит в систему в момент, когда заняты все каналы, а в очереди стоят k заявок, то она будет ждать в очереди в среднем k/nμ.
Если заявка приходит в систему в момент, когда заняты все каналы, а в очереди стоят m заявок, то она не будет ждать, так как покинет систему.
Среднее время ожидания определим из выражения
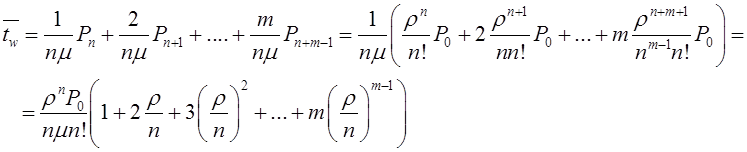 (23)
(23)
Это выражение отличается от выражения для средней длины очереди только множителем 1/ρμ=λ, откуда
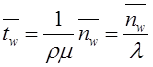
т.е., результат, вытекающий из формулы Литтла, или
Среднее время пребывания заявки в системе.
Так же как и в случае с одноканальной СМО имеем:
Пример 0‑1.
В парикмахерской работают 3 мастера, для очереди посетителямив в зале ожидания предусмотрены 3 места. Клиенты приходят в среднем один раз в 4 минуты, обслуживание длится в среднем 15 мин. Требуется определить относительную и абсолютную пропускные способности парикмахерской, среднее число клиентов, ждущих обслуживани,я, и среднее время нахождения клиента в парикмахерской.
Имеем:
n=3,
m=3,
l=1/4=0,25,
m=1/15,
ρ =15/4=3,75,
χ=ρ /n=1,25.
Находим ![]() :
:
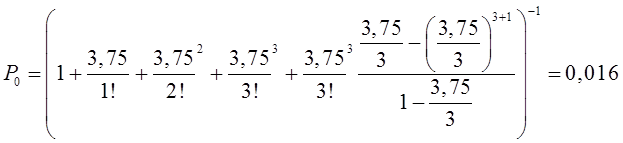
и вероятность отказа в обслуживании.
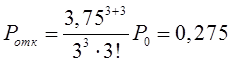
Относительная пропускная способность парикмахерской:
![]()
Абсолютная пропускная способность:
![]()
Среднюю длину очереди
находим на основе формулы 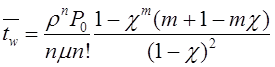 (24):
(24):
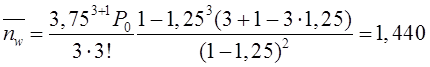
Среднее время нахождения
клиента в парикмахерской определяется с помощью 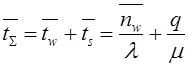 (25):
(25):
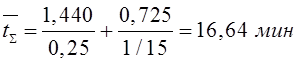
1. Многие задачи анализа и проектирования можно решить с использованием моделей систем массового обслуживания. Это дает возможность применять модели теории с тем же названием, многие из моделей которой получены на основе теории марковских процессов.
2. Основными показателям моделей систем с отказами являются относительная и абсолютная пропускная способность, а также вероятность отказа в обслуживании. Эти показатели для стационарного режима могут быть найдены на основе математических выражений.
3. Важными показателями для системы с ожиданием являются показатели, характеризующие нахождение заявок в очереди. Анализ таких систем может производиться в случае пуассоновского входящего потока на основе формулы Хинчина-Полачека.
4. Модели СМО можно применять для решения разнообразных практических задач. В частности, на примерах данной темы показано, как с помощью модели многоканальной СМО отказами можно решить задачу оптимизации числа каналов по критерию величины прибыли, а с помощью модели СМО с очередью определить требования к размерам заявок для уменьшения размера очереди и связанного с ней размера буферного накопителя.
1. Приведите примеры СМО с отказами.
2. Дайте краткое описание модели СМО с отказами.
3. Как получаются выражения для характеристик СМО с отказами?
4. Что такое относительная пропускная способность СМО с отказами?
5. Что такое абсолютная пропускная способность?
6.
Как рассчитывается вероятность![]() одноканальной СМО?
одноканальной СМО?
7.
Как рассчитывается вероятность![]() одноканальной СМО?
одноканальной СМО?
8. Чему равна вероятность отказа обслуживания заявки в многоканальной СМО с отказами?
9. Как подсчитывается среднее число заявок в многоканальной системе с отказами?
10. Как можно определить структуру (число каналов) многоканальной СМО по критерию максимума получаемой прибыли?
11. Какими показателями характеризуется функционирование одноканальной СМО с неограниченной очередью?
12. Что такое дисциплина обслуживания? Назовите примеры наиболее известных дисциплин.
13. Что позволяет определить формула Хинчина-Полачека? Для каких случаев справедлива формула?
14. Какие распределения времени обслуживания в одноканальной СМО с неограниченной очередью представляют наибольший интерес для практики? Опишите эти случаи.
15. Какие основные факторы влияют на значения показателей одноканальной СМО с неограниченной очередью?
16. Каким образом можно улучшить характеристики функционирования одноканальной СМО с неограниченной очередью?
1. Емельянов А.А. Модели процессов массового обслуживания // Прикладная информатика, 2008, № 5 (17), с. 92-130.
2. Емельянов А.А. Стохастические сетевые модели массового обслуживания // Прикладная информатика, 2009, № 5 (23), с. 103-111.
· изучить сущность моделирования на основе метода статистических испытаний.
· изучить схему и границы применимости метода статистических испытаний;
· изучить основные принципы компьютерной имитации случайных величин;
· изучить способы имитации случайных событий.
получите представление о:
· когда применяется и как практически реализуется модель на основе метода статистических испытаний;
· достоинства и недостатки метода статистических испытаний;
будете знать:
· как практически создаются и реализуются программные модели на основе метода статистических испытаний.
1. Метод статистических испытаний.
2. Случайные и псевдослучайные числа.
3. Имитация случайных событий.
4. Пример применения метода Монте-Карло.
Аналитические модели, рассмотренные ранее, могут с успехом применяться на этапе системного анализа и для решения ряда задач этапа проектирования, когда требования к точности результата не являются слишком строгими. Такими задачами могут быть задачи выбора конфигурации или модели сервера, где требуется определить только класс выбираемого устройства или подсистемы.
Однако в ряде практических ситуаций применение аналитических моделей приводит к большой потере точности получаемого результата из-за того, что модели строятся на слишком приблизительном описании реальных процессов. В этих случаях можно использовать подход на основе имитационного моделирования процессов, который позволяет практически с любой степенью точности описать исследуемые процессы и отличается универсальностью применения.
Рассмотрение имитационных моделей начнем с метода статистических испытаний.
Статистическое моделирование является разновидностью имитационного моделирования и состоит в обработке данных о системе (модели) с целью получения статистических характеристик системы. Чаще всего оно применяется как способ исследования процессов поведения систем в условиях, когда внутренние взаимодействия в системах неизвестны, и построение аналитической модели явления затруднено или вовсе неосуществимо. Метод может применяться и на этапе системного анализа информационных систем, но основными для его применения являются задачи исследования операций, массового обслуживания и многие другие, связанные со случайными процессами. Эти задачи возникают в основном на этапах системного проектирования и разработки.
Смысл метода Монте-Карло состоит в том, что исследуемый процесс моделируется путем многократных повторений его случайных реализаций (рис. 20).
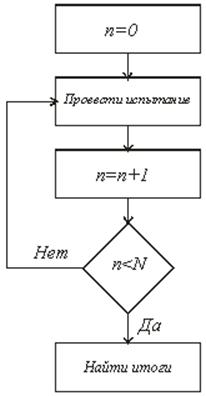
Рис. 20. Блок-схема метода Монте-Карло
Единичные реализации называются статистическими испытаниями, в силу чего метод называется также методом статистических испытаний.
Пусть, например, нам требуется найти значение числа π. Изобразим на декартовой плоскости две фигуры – квадрат и сектор круга, как это показано рис. 21:
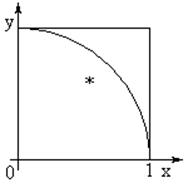
Рис. 21. Нахождение числа π методом Монте-Карло
Предположим, что мы имеем генератор случайных чисел в диапазоне от [0;1], которые будем считать координатами x и y точки декартовой плоскости. Точка будет принадлежать области круга, если выполняется условие
![]()
Тогда после многократно проведенных испытаний значение числа π можно приближенно оценить по формуле
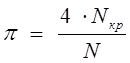
где
![]() - число попаданий точки в область круга;
- число попаданий точки в область круга;
![]() - число
попаданийточки в область квадрата (т.е., общее число реализаций).
- число
попаданийточки в область квадрата (т.е., общее число реализаций).
Метод применяется в тех случаях, когда построение аналитической модели явления затруднено или вовсе неосуществимо, например, при решении сложных задач теории массового обслуживания и ряда других задач исследования операций, связанных с изучением случайных процессов. В зависимости от особенностей решаемых задач метод Монте-Карло имеет ряд разновидностей и модификаций, которые повышают как точность результата, так и вычислительную эффективность процедуры.
Недостатком метода Монте-Карло являются большие затраты машинного
времени, требуемые для достижения большей статистической точности: известно,
что для уменьшения дисперсии результата в k раз, число испытаний
необходимо увеличить в ![]() раз.
раз.
В основе вычислений по методу статистических испытаний лежит случайный выбор чисел из заданного вероятностного распределения. Чисто случайные последовательности выдают аппаратурные средства, например, базирующиеся на усилении и обработке теплового шума электронных схем.
При практических вычислениях эти числа берут из таблиц или получают путем выполнения некоторых операций, результатами которых являются псевдослучайные числа с теми же свойствами, что и числа, получаемые путем случайной выборки. Имеется большое число вычислительных алгоритмов, которые позволяют получить длинные последовательности псевдослучайных чисел (последовательности (имеющие цикл повтора, но очень длительный). Реализующие эти алгоритмы программы называются генераторами случайных чисел.
Имеется большое число вычислительных алгоритмов, которые позволяют получить длинные последовательности псевдослучайных чисел. Один из наиболее простых и эффективных вычислительных методов получения последовательности равномерно распределенных на интервале [0,1] случайных чисел, включающий только одну операцию умножения, разработан Лехмером и известен как метод линейного конгруента.
Алгоритм имеет четыре параметра:
m модуль (основание системы), m > 0
a множитель, 0 ≤ a < m
c приращение, 0 ≤ с < m
![]() начальное
значение,
начальное
значение, ![]()
Последовательность случайных чисел {Xn} получается с помощью следующего итерационного равенства:
![]()
Если m, а и с - целые,
то создается последовательность целых чисел в диапазоне ![]() .
.
Выбор значений а, с и m является критичным для разработки хорошего генератора случайных чисел.
Очевидно, что m должно быть очень большим, чтобы была возможность создать множество случайных чисел. Считается, что m должно быть приблизительно равно максимальному положительному целому числу для данного компьютера. Для 32-х разрядных ЭВМ обычно значение m близко или равно 231.
Значения а, с и m должны быть выбраны таким образом, чтобы эти три критерия выполнялись. В соответствии с первым критерием можно показать, что если m является простым и с = 0, то при определенном значении а период, создаваемый функцией, будет равен m-1. Для 32-битной арифметики соответствующее простое значение m = 231 - 1. Таким образом, функция создания псевдослучайных чисел имеет вид:
![]()
Только небольшое число значений а удовлетворяет всем трем критериям. Одно из таких значений а = 75 = 16807, которое использовалось в семействе компьютеров IBM 360.
Для задания базового значения в программе использовано битовое содержимое таймера компьютера, что обеспечивает случайных характер выбора начальной точки последовательности чисел. Это удобно для проведения экспериментов на модели, но создает сложности в процессе ее отладки, так как не дает возможность обеспечить воспроизводимость запусков. С целью обойти эту проблему следует задавать в качестве начального значения конкретную величину, одну и ту же для всех отладочных тестов.
Программа на языке С++ может быть реализована в виде (начальное значение bx получается путем считывания с компьютерного таймера):
double rundum(void)
{
long static bx = (long)time(NULL);
unsigned long m =2<<31 - 1;
if (bx % 2 == 0) bx++;
bx = (16807 * bx) % m ;
return((long double) bx / (long double)m);
}
В случае, если начальное значение bx четное, оно заменяется на ближайшее большее нечетное для улучшения свойств получаемой последовательности.
Для получения случайной величины y, равномерно распределенной на интервале (a,b), можно воспользоваться выражением
![]()
где
x - случайная величина, равномерно распределенная на интервале (0,1).
Программа на языке С++:
double unifrm (float m , float s)
{
return ( m-s + 2*s*rundum() );
}
Во многих программах, которые реализуют метод Монте-Карло необходимо уметь имитировать наступление некоторых событий, например, нахождение некоторого устройство в рабочем или нерабочем состоянии для решения задачи оценивания надежности системы, которая включает это устройство. Для этого используется следующий метод.
Пусть некоторое событие А происходит с вероятностью РА. Требуется воспроизвести факт наступления события А.
Поставим в соответствие событию А событие В, состоящее в том, что х ≤ РА, где х случайное число с равномерным на интервале (0,1) законом распределения. Вычислим вероятность события В:
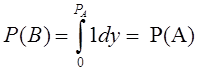
Таким образом, события А и В являются равновероятными. Отсюда вытекает процедура имитации факта появления события А. Она сводится к проверке неравенства х ≤ РА, и алгоритм заключается в следующем:
1) Генерируется случайное число х;
2) Проверяется выполнение неравенства х ≤ Р(А);
3) Если неравенство выполняется, считается, что событие А произошло, если нет – не произошло.
Программа на языке С++:
int event(double P)
{
if (rundum()<= P) return (1); else return (0);
}
Функция event возвращает значение 1 в случае наступления в очередном испытании события с вероятностью Р, и 0 в противном случае.
Рассмотрим теперь, как практически применяется метод Монте-Карло к решению задачи оценивания надежности простой структуры, изображенной на рис 22.
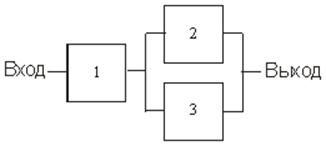
Рис. 22. Пример для метода Монте-Карло
Для каждого из блоков 1, 2, 3 заданы вероятности их нахождения в работоспособном состоянии. Считая, что вся схема находится в работоспособном состоянии в случае, если между входом и выходом существует хотя бы одна цепочка работоспособных блоков, необходимо оценить вероятность ее нахождения в работоспособном состоянии.
Решить эту задачу без особого труда можно с помощью теории вероятностей.
Действительно, сначала заменим блоки 2 и 3 одним блоком с эквивалентной надежностью. Возможными исходами для этого фрагмента схемы будут:
![]()
![]()
![]()
![]()
где
![]() означает работоспособность, а
означает работоспособность, а ![]() -
неработоспособность блока с номером i. Полезными
исходами являются первые три из перечисленных, вероятность наступления одного
из которых находится как сумма вероятностей наступления каждого:
-
неработоспособность блока с номером i. Полезными
исходами являются первые три из перечисленных, вероятность наступления одного
из которых находится как сумма вероятностей наступления каждого:
![]()
Поскольку все перечисленные исходы составляют полную группу событий, то
![]()
и
![]()
Поскольку
события ![]() независимы,
то
независимы,
то
![]()
а так как вероятность
противоположного события ![]() находится как
разность между 1 вероятностью самого события, то
находится как
разность между 1 вероятностью самого события, то
![]()
Вся схема будет работоспособна, если одновременно будут работоспособны блок 1 и «виртуальный» блок 23. Поскольку эти события можно считать независимыми, то вероятность одновременного наступления этих событий найдется как произведение вероятностей каждого из событий, т.е.:
![]() (1)
(1)
![]() есть надежность всей схемы.
есть надежность всей схемы.
Например, для значений вероятностей блоков 1, 2, 3 равных соответственно 0,95; 0,9; 0,85 расчет по формуле (1) (1) дает 0,93575.
Решим теперь эту же задачу, воспользовавшись схемой метода Монте-Карло. Целью каждого испытания будет проверка работоспособности схемы. Смоделировать исход каждого испытания в компьютерной модели можно в два этапа: сначала сымитировать работоспособность или поломку каждого из трех блоков, а затем определить конечный результат.
Первый этап реализуется как имитация наступления события с заданной вероятностью, процедура которой уже была рассмотрена.
Второй этап состоит в
проверке истинности логического условия, которое в данном случае выглядит как: ![]() .
.
Программная модель на языке С++ имеет вид:
|
// Модель надежности // Заголовочные файлы -------------------------------------------------------------------------------------------------------------- |
|
|
#include «stdafx.h» |
//стандартные заголовки |
|
#include <time.h> |
//функции работы с системным временем (time) |
|
#include <io.h> |
//для функции creat() |
|
#include <fstream.h> |
//потоковый класс |
|
#include <sys\stat.h> |
//значения параметров amode |
|
#include <iomanip.h> |
//манипуляторы ввода-вывода |
|
// Параметры запуска модели --------------------------------------------------------------------------------------------------- |
|
|
long N=100; |
//число испытаний |
|
double P1=0.95; |
//надежность блока 1 |
|
double P2=0.9; |
//надежность блока 2 |
|
double P3=0.85; |
//надежность блока 3 |
|
// Равномерное распределение [0,1] (конгруэнтный алгоритм) ------------------------------------------------------------- |
|
|
double rundum (void) { |
|
|
long static bx = (long)time(NULL); |
|
|
unsigned long m =2<<31 - 1; |
|
|
if (bx % 2 == 0) bx++; |
|
|
bx = (16807 * bx) % m ; |
|
|
return((long double) bx / (long double)m); |
|
|
} |
|
|
//Имитация наступления события с заданной вероятностью P int event (double P) { if (rundum()<= P) return (1); else return (0); } |
|
|
------------------------------------------------------------------------------------------------------------------------------------------------ int APIENTRY WinMain(HINSTANCE hInstance,HINSTANCE hPrevInstance, LPSTR lpCmdLine,int nCmdShow) { |
|
|
//Организация вывода результатов------------------------------------------------------------------- int reportfile=creat («D:\\MyResults.txt», S_IWRITE); //создание файла ofstream fileOut; //выводной класс fileOut.attach (reportfile); //включение в поток ==================================================================================== long suml; //накопитель long i; //индекс for(i = 0, suml=0; i < N; i++) if ( event (P1) && (event (P2) || event (P3) ) ) suml++; fileOut << «Всего испытаний =« << N << endl << «Надежность=« << (float)suml/N << endl; //=============================================================================== return(0); } |
|
Значения параметров моделирования задаются в разделе с заголовком (строкой комментария) «Параметры запуска модели». Здесь задаются число повторений экспериментов N и вероятности работоспособности блоков P1, P2, P3.
Значения равномерно распределенного в промежутке [0,1] случайного числа получаются с помощью функции rundum, построенной на основе уже рассмотренного в данной теме конгруентного алгоритма.
Функция event позволяет имитировать наступление события с заданной вероятностью (также рассмотрена ранее).
Оценка вероятности
работоспособного состояния находится как отношение счетчика числа успешных
испытаний ![]() к общему числу испытаний N.
к общему числу испытаний N.
Результаты выводятся в файл, обозначаемый переменной reportfile.
Если провести запуски
программы с числом испытаний ![]() равным 100,
1000 и 1000000, то результатами будут значения надежности 0,93; 0,947 и 0,936093.
равным 100,
1000 и 1000000, то результатами будут значения надежности 0,93; 0,947 и 0,936093.
1. Аналитические модели во многих практических ситуациях не могут обеспечить требуемой точности результатов. Универсальным средством преодолеть эти трудности является методология имитационного моделирования, практически не имеющая ограничений в смысле возможных применений и точности получаемых с ее помощью оценок показателей системы.
2. В случае, когда задача нахождения значений показателей изучаемого процесса не требует воспроизведения процесса в динамике и в модель не включаются описания внутренних механизмов протекания процессов, весьма полезным является применение метода статистических испытаний. Его схема отличается простотой, реализация на компьютере не требует специальных средств, однако для сложных задач сопряжена с большим расходованием времени на проведение машинных экспериментов.
3. Реализация машинных экспериментов в условиях действия случайных факторов требует использования генераторов случайных чисел и имитаторов случайных событий. Для построения генераторов и имитаторов разработаны специальные алгоритмы, обеспечивающие получение с помощью построенных на их основе компьютерных программ необходимых результатов с требуемыми характеристиками.
1. Что такое компьютерное моделирование, и в каких случаях целесообразно его применять?
2. В чем заключается идея метода статистических испытаний?
3. Когда следует применять метод статистических испытаний?
4. Из каких шагов состоит вычислительная процедура метода статистических испытаний?
5. Поясните применение метода статистических испытаний на примере определения надежности схемы.
6. Чем достигается статистическая точность метода статистических испытаний?
7. Как зависит точность результата, полученного на основе метода статистических испытаний, от числа проведенных испытаний?
8. В чем заключаются основные достоинства и недостатки метода статистических испытаний?
1. Емельянов А.А., Власова Е.А., Дума Р.В., Емельянова Н.З. Компьютерная имитация экономических процессов: Учебник / Под ред. А.А. Емельянова. – М.: Маркет ДС, 2010. – 464 с.
· изучить сущность имитационного моделирования систем и процессов.
· изучить принципы построения имитационных моделей;
· изучить способы имитации случайных величин и событий;
· изучить методы обработки результатов имитационного моделирования.
получите представление о:
· когда применяется и как реализуются имитационные модели;
· как имитируется в программной модели параллельное протекание реальных процессов;
· способах преобразования описаний в исполнительные компьютерные программы;
будете знать:
· какие алгоритмы используются для имитации случайных величин с заданным законом распределения;
· как реализуется имитация в программе случайного события с заданной вероятностью;
· как найти математическое ожидание и дисперсию показателя на основе полученных с помощью модели данных.
1. Концепции имитационного моделирования.
2. Имитация случайных величин с заданными законами распределения.
3. Обработка результатов запусков программной модели.
Ранее нами была рассмотрена модель марковских процессов, которую можно с успехом применять для решения многих практических задач оценивания показателей системы с помощью аналитических выражений. Однако условия марковости процесса соблюдаются далеко не всегда. Кроме того, получение аналитических выражений для расчета показателей часто представляет большую трудность. Альтернативным подходом к решению задач оценки показателей является исследование системы на основе имитационной модели, с помощью которой можно получить результаты для случаев произвольных распределений временных интервалов и других случайных величин. Такую модель можно построить с помощью специальной моделирующей системы, что ускоряет процесс создания, улучшает характеристики конечного результата (программной модели) и имеет ряд других достоинств.
Поведение
(процесс функционирования) динамической дискретной системы можно рассматривать
как последовательность состояний ![]() в моменты времени
в моменты времени ![]() . При этом факты смены состояния системой
рассматриваются как события. В основу идеи имитационного моделирования
положен принцип, согласно которому на ЭВМ осуществляется воспроизведение (имитация)
процесса функционирования исследуемой системы в контексте смены ее состояний в
результате происходящих в ней событий. В процессе проведения имитации
собираются данные о состоянии системы или отдельных ее элементов в определенные
моменты времени, что позволяет в конце процесса моделирования провести
агрегирование и обработку собранных данных и получить значения нужных
исследователю показателей.
. При этом факты смены состояния системой
рассматриваются как события. В основу идеи имитационного моделирования
положен принцип, согласно которому на ЭВМ осуществляется воспроизведение (имитация)
процесса функционирования исследуемой системы в контексте смены ее состояний в
результате происходящих в ней событий. В процессе проведения имитации
собираются данные о состоянии системы или отдельных ее элементов в определенные
моменты времени, что позволяет в конце процесса моделирования провести
агрегирование и обработку собранных данных и получить значения нужных
исследователю показателей.
Пусть, например, нам необходимо исследовать работу уже рассматривавшейся выше СМО с очередью и одним обслуживающим прибором (рис. 15.). Заявки, образующие входящий поток, поступают в систему в случайные моменты времени. Если обслуживающий прибор (канал) свободен, заявка принимается на обслуживание, которое продолжается некоторое время (его величина является, как правило, также случайной), после чего она уходит из системы (выходящий поток). Если в момент прихода заявки канал занят, заявка попадает в очередь ждущих заявок.
Решая задачу
нахождения показателей системы, для описания состояния процесса достаточно
использовать один параметр ![]() , который означает число заявок в системе в момент времени
, который означает число заявок в системе в момент времени ![]() . Имитацию
процесса обслуживания заявки в можно провести, определяя моменты ожидаемого
изменения состояния (наступления события), связанных с изменением состояния
. Имитацию
процесса обслуживания заявки в можно провести, определяя моменты ожидаемого
изменения состояния (наступления события), связанных с изменением состояния
![]() . В данном случае, это моменты поступления
очередной заявки в систему и моменты окончания обслуживания заявки, находящейся
в обслуживающем приборе. Моменты наступления будущих событий могут быть найдены
на основе рекуррентных выражений с помощью функций распределения интервалов
времени путём проведения случайных испытаний аналогично тому, как это производилось
в методе статистических испытаний. Это позволяет построить алгоритм имитации,
состоящий из повторения следующей совокупности шагов:
. В данном случае, это моменты поступления
очередной заявки в систему и моменты окончания обслуживания заявки, находящейся
в обслуживающем приборе. Моменты наступления будущих событий могут быть найдены
на основе рекуррентных выражений с помощью функций распределения интервалов
времени путём проведения случайных испытаний аналогично тому, как это производилось
в методе статистических испытаний. Это позволяет построить алгоритм имитации,
состоящий из повторения следующей совокупности шагов:
· находится момент наступления ближайшего события, событие с минимальным временем — наиболее раннее событие;
· стрелки модельных часов передвигаются на этот момент времени;
· определяется тип происшедшего события;
· в зависимости от типа события модифицируются значения переменных, описывающих состояние системы (в данном случае, число находящихся в системе заявок), и определяются следующие моменты наступления событий.
Логика построения мехнизма моделирования показана на рис. 23.
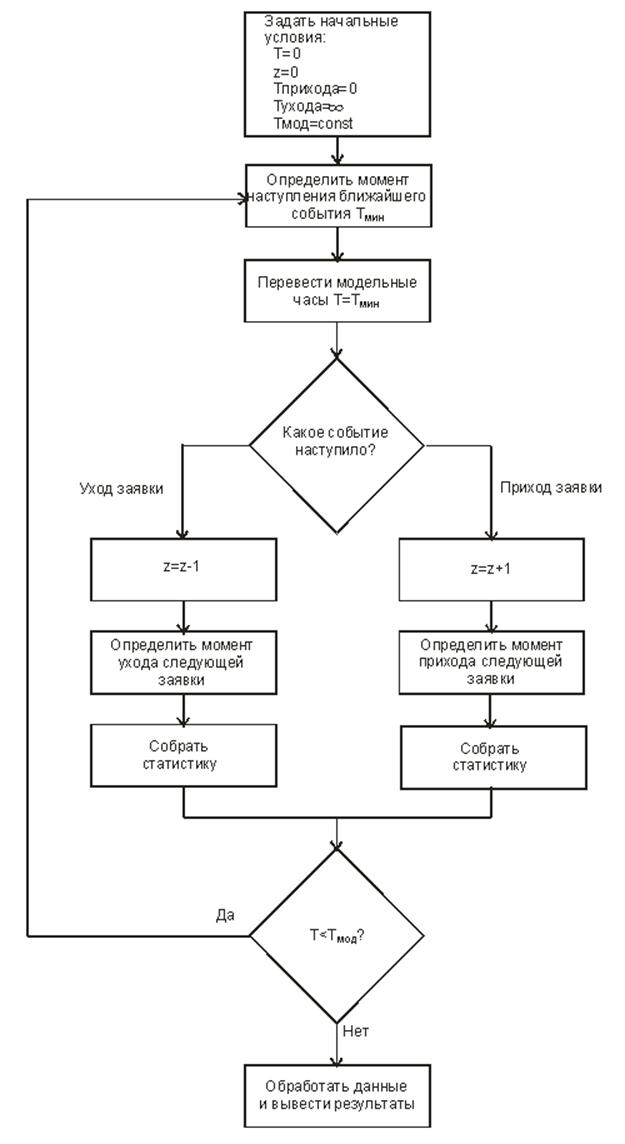
Рис. 23. Блок-схема имитации работы одноканальной СМО с очередью
В процессе выполнения алгоритма производится накопление значений существенных параметров моделируемой системы. По окончании моделирования осуществляется статистическая обработка полученных величин и выдача результатов. Описанный алгоритм носит название событийного алгоритма.
Альтернативным способом построения алгоритма имитационного моделирования является перемещение по временной оси с фиксированным интервалом (шагом). После каждого перехода на новую временную отметку проводится сканирование всех протекающих в моделируемой системе процессов и выявление всех свершившихся на данный момент существенных событий. Такой алгоритм носит название пошагового алгоритма.
Преимуществом пошагового алгоритма является простота его программной реализации. Вместе с тем, в условиях, когда наступление событий, обусловленных разными процессами, происходит с сильно отличающимися интервалами, то значительное время моделирования оказывается затраченным впустую (например, при моделировании производственного процесса на предприятии, работающем в односменном режиме, все вечернее и ночное время программная модель не будет выполнять никакой содержательной работы). Поэтому большинство программных реализаций имитационных моделей использует событийный алгоритм имитации.
Имитационное моделирование представляет собой процесс, реализуемый с помощью средств вычислительной техники, что позволяет автоматизировать решение таких задач как:
а) Создание или модификация имитационной модели.
б) Проведение модельных экспериментов и интерпретация получаемых результатов.
В случаях разработки сложных моделей, предназначенных для проведения большого объема экспериментов, для решения этих задач используются моделирующие комплексы (системы).
Имитационное моделирование как информационная технология включает несколько основных этапов.
На этапе структурного анализа процессов проводится формализация реального процесса, его декомпозиция на подпроцессы, которые могут также подвергаться декомпозиции. Задачи, решаемые на этом этапе, соответствуют задачам создания модели деловых процессов, вместе с тем, в зависимости от применяемых средств моделирования результат может потребовать преобразования формы представления в вид, наиболее полно соответствующий задачам, решаемым на дальнейших шагах.
Описание модели в вербальном, графическом или полуформализованном виде должно быть представлено на специальном (формальном) языке для ввода в моделирующую систему. При этом могут применяться:
· Ручной способ. Описание составляется на языке какой-либо системы моделирования, например, GPSS, Pilgrim или алгоритмическом языке, например, Visual Basic (размер результирующего текста в последнем случае будет многократно превосходить размер текста на языке специальных систем).
· Автоматизированный способ. Текст на формальном языке получается в результате автоматической генерации описания, которое строится в интерактивном режиме с помощью высокоуровневого графического конструктора. Такой конструктор, которым оснащена, в частности, система Pilgrim, позволяет фактически совместить этап разработки программной модели с этапом системного анализа.
Созданное формальное описание далее преобразуется в компьютерную программу, способную воспроизводить реальные процессы. Преобразование, которое обычно представляет собой трансляцию и редактирование связей, осуществляется в некоторой программной среде, может проводиться в двух режимах.
· Интерпретация. В этом режиме специальная программа-интерпретатор осуществляет всю процедуру имитации, непосредственно выполняя инструкции формального описания. Примером системы, где предусмотрен режим интерпретации, является система GPSS.
· Компиляция. В этом режиме на основе формального описания создается отдельная программа (исполнительный модуль), который может запускаться независимо от программной среды, в которой он был создан. Примером системы, где предусмотрен режим интерпретации, является система Pilgrim.
Целью следующего этапа является обоснование модели, заключающегося в демонстрации пригодности модели для получения нужных показателей, т.е., обеспечение необходимых точности и надежности получаемых на ее основе результатов.
Основной, последний этап моделирования сводится к проведению машинных экспериментов с программной моделью, сбору, накоплению, обработке и анализу собранных данных.
Значительную роль в программных средствах и системах имитационного моделирования играют методы и процедуры получения случайных величин, подчиняющихся тому или иному закону распределения. Рассмотрим основные из этих методов, а также приемы обработки результатов, получаемых с помощью имитационных моделей.
Пусть непрерывная случайная
величина ![]() задана законом распределения:
задана законом распределения:
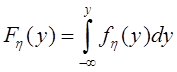
где
![]() –
плотность распределения вероятностей,
–
плотность распределения вероятностей,
![]() - функция распределения вероятностей. Тогда случайная
величина
- функция распределения вероятностей. Тогда случайная
величина ![]() .
.
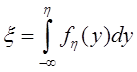
распределена равномерно на интервале (0,1).
Отсюда следует, что искомое значение y может быть определено из уравнения:
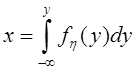
которое эквивалентно уравнению:
![]()
где
y – значение случайной величины ![]() ,
,
x – значение случайной величины ![]() .
.
Решение уравнения можно
записать в общем виде через обратную функцию ![]() :
:
![]()
Основной недостаток метода заключается в том, что интеграл не всегда является берущимся, а уравнение не всегда решается аналитическими методами.
Имитация величины, распределенной по показательному закону.
Для ряда весьма важных случаев решение уравнения для нахождения значения случайной величины можно найти. В частности, в соответствии с методом обратной функции существует преобразование, позволяющее вычислить значения случайной величины η, распределенной по показательному закону, который особенно часто используется для исследования систем массового обслуживания и определения показателей надежности систем.
Функция плотности для показательного закона имеет вид:
![]()
Воспользуемся методом обратной функции, вычислим интеграл и получим уравнение вида
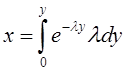
или
![]()
Тогда ![]() и, прологарифмировав и разрешив уравнение
через y, будем иметь:
и, прологарифмировав и разрешив уравнение
через y, будем иметь:
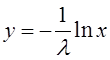
Получая значение х с помощью датчика равномерно распределенных на интервале (0,1) случайных чисел, можно получить значения y в соответствии с полученным выражением.
Программа на языке С++:
float expont(float m )
{
return(m*(-log(rundum()) ) );
}
Имитация случайного числа по данным наблюдения.
Довольно часто значения случайной величины доступны в виде данных наблюдения, которые можно непосредственно использовать для модельных экспериментов без аппроксимации теоретическим распределением.
Предположим, что в банке регистрировалось число обращений k его клиентов за получением обслуживания в часовом интервале, на основе чего получены частоты fk появлений в течение часа к клиентов:
|
k |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
fk |
3 |
19 |
23 |
21 |
6 |
4 |
2 |
1 |
1 |
Вычислим значение 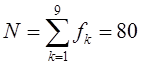 и дополним таблицу строкой со значениями
и дополним таблицу строкой со значениями 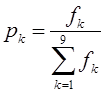 :
:
|
k |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
fk |
3 |
19 |
23 |
21 |
6 |
4 |
2 |
1 |
1 |
|
pk |
0,0375 |
0,2375 |
0,2875 |
0,2625 |
0,0750 |
0,0500 |
0,0250 |
0,0125 |
0,0125 |
и строкой ![]() , в первой ячейке
, в первой ячейке ![]() которой
будет записано значение
которой
будет записано значение ![]() , а в оставшихся
– значения
, а в оставшихся
– значения ![]() :
:
|
k |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
fk |
3 |
19 |
23 |
21 |
6 |
4 |
2 |
1 |
1 |
|
pk |
0,0375 |
0,2375 |
0,2875 |
0,2625 |
0,0750 |
0,0500 |
0,0250 |
0,0125 |
0,0125 |
|
Pk |
0,0375 |
0,2750 |
0,5625 |
0,8250 |
0,9000 |
0,9500 |
0,9750 |
0,9875 |
1,0000 |
Если считать, что значения ![]() хранятся в массиве P[9] (с индексом
первого элемента равным 1), то построенный на основе метода обратной функции
алгоритм получения случайной величины k для
данного примера можно записать в таком виде:
хранятся в массиве P[9] (с индексом
первого элемента равным 1), то построенный на основе метода обратной функции
алгоритм получения случайной величины k для
данного примера можно записать в таком виде:
a=x
k=0
ЦИКЛ-ПОКА a ≤ P[k+1] И k≤8
k=k+1
ВСЕ-ЦИКЛ
где
x – значение псевдослучайного числа, равномерно распределенного на интервале 0,1.
Приводимый ниже текст программы на языке С++ обеспечивает генерацию случайной величины с произвольными значениями, которые задаются элементами массива vals. Массив nums задает значения частот появления значений (обозначены в примере как fk). Аргумент parts – число значений случайной величины (в примере - 9).
float partval(int parts, int nums[], float vals[])
{
int i;
float sum, bleft,rnd=rundum();
for (i=0,sum=0; i<parts; i++) sum+=nums[i];
for (i=0, bleft=0; i<parts && rnd>=bleft; bleft+=(float)nums[i]/sum, i++) ;
return(vals[i-1]);
}
В процессе имитационного моделирования формируется большое количество реализаций, являющихся исходным статистическим материалом для нахождения приближенных значений (оценок) показателей эффективности. Основные результаты моделирования включают, как правило, функцию распределения (наиболее информативное описание) какого-то состояния системы или процесса (события, явления) и/или числовые характеристики, такие как оценка вероятности, математическое ожидание и дисперсия случайной величины.
Оценка вероятности.
В качестве оценки вероятности используется частота
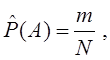
где
m - число случаев наступления события А в экспериментах,
N - число проведенных экспериментов.
Для получения оценки вероятности обычно организуют на программном уровне два счетчика, в которых накапливаются:
· общее количество проведенных экспериментов N;
· общее количество экспериментов с положительным исходом m.
В ряде случаев в качестве характеристики исследуемой системы выступает закон распределения (плотности распределения). Его приближенно можно представить с помощью гистограммы.
Для этого
интервал изменения случайной величины разбивается на отрезки ![]() , каждому из них сопоставляется счетчик,
где накапливаются mi –
количество попаданий значений этой величины
, каждому из них сопоставляется счетчик,
где накапливаются mi –
количество попаданий значений этой величины ![]() .
.
На основании
полученных значений счетчиков для ![]() можно
построить гистограмму - набор прямоугольников с высотами
можно
построить гистограмму - набор прямоугольников с высотами ![]() . Практический прием сбора данных и
построения графика вместе с текстом компьютерной программы будет рассмотрен
далее.
. Практический прием сбора данных и
построения графика вместе с текстом компьютерной программы будет рассмотрен
далее.
Оценка математического ожидания.
Оценку
математического ожидания ![]() получают как среднее
арифметическое значение случайной величины yi:
получают как среднее
арифметическое значение случайной величины yi:
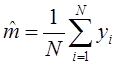
Для получения суммы в программных моделях обычно используется переменная, значение которой получает приращение после каждого проведенного испытания.
Оценка дисперсии получается с помощью формулы:
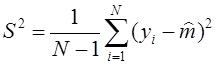
1. Применение метода статистических испытаний дает хорошие результаты в случаях, когда требуется найти статические характеристики системы. Для моделей динамических систем и, в первую очередь, для стохастических моделей мощным инструментом решения задач является имитационное моделирование, воспроизводящее с помощью ЭВМ протекание реальных процессов.
2. Для реализации программных моделей применяются стандартные механизмы имитации событий. В случае, когда необходимо добиться наиболее быстрого выполнения алгоритма обычно применяется событийный алгоритм имитации.
3. Создание имитационных моделей требует выполнения ряда задач в определенной последовательности. Непосредственная реализация программы может осуществляться на основе интерпретации или компиляции. Каждый из этих вариантов имеет свои достоинства и недостатки, выбор подхода обусловлен требованиями конкретной задачи.
4. В имитационных моделях стохастических систем широко используются случайные величины, распределенные по определенным законам. Для получения таких величин используются различные методы и приемы, одним из наиболее распространенных является метод обратной функции.
5. Данные, полученные в результате прогона имитационных моделей, необходимо обрабатывать. В зависимости от типа результатов используются свои методы обработки. Типичными случаями обработки данных запусков стохастических моделей являются получение средних значений и дисперсии какого-либо показателя, для вычисления которых по собранным данным применяются соответствующие математические выражения.
1. Что такое имитационное моделирование?
2. Для решения каких задач используется имитационное моделирование?
3. Что такое пошаговый алгоритм имитации протекания процессов?
4. Что такое событийный алгоритм имитации протекания процессов?
5. Каковы сравнительные достоинства и недостатки пошагового и событийного алгоритмов?
6. Из какие основных этапов состоит процесс моделирования?
7. В чем заключается задача этапа структурного анализа процессов?
8. Какие способы используются для формализации содержательного описания модели?
9. Какие способы используются для получения программного кода по формальному описанию модели?
10. Как реализуется метод обратной функции для имитации случайной величины, распределенной по показательному закону?
11. Как оценить величину вероятности наступления события по результатам моделирования?
12. Как оценить математическое ожидание случайной величины по результатам моделирования?
13. Как оценить дисперсию случайной величины по результатам моделирования?
1. Емельянов А.А., Власова Е.А., Дума Р.В. Имитационное моделирование экономических процессов / Под ред. А.А. Емельянова. – М.: Финансы и статистика, 2009. – 480 с.
· изучить сущность подхода на основе методологии имитационного моделирования к анализу и синтезу информационных процессов и систем.
· изучить сущность и границы применимости метода статистических испытаний;
· изучить основные принципы компьютерной имитации стохастических процессов;
· понять возможности моделирующих комплексов для создания и применения имитационных моделей.
получите представление о:
· когда применяется и как практически реализуется модель на основе метода статистических испытаний;
· принципах построения и механизме программной имитации стохастических процессов;
будете знать:
· как можно создавать модели с помощью систем имитационного моделирования;
· из чего состоят и как следует анализировать результаты прогонов программной модели.
1. Создание имитационных моделей с помощью систем моделирования.
2. Конструкционные элементы модели системы Pilgrim.
3. Средства описания модели в системе Pilgrim.
Имитационную модель нужно создавать. Для этого необходимо специальное программное обеспечение - система моделирования (simulation system). Специфика такой системы определяется технологией работы, набором языковых средств, сервисных программ и приемов моделирования.
Имитационная модель должна отражать большое число параметров, логику и закономерности поведения моделируемого объекта во времени (временная динамика) и в пространстве (пространственная динамика). Моделирование объектов экономики связано с понятием финансовой динамики объекта.
Имитационное моделирование представляет собой процесс, реализуемый с помощью средств вычислительной техники, позволяющий автоматизировать решение таких задач как:
1) Создание или модификация имитационной модели.
2) Проведение модельных экспериментов и интерпретация получаемых результатов.
В случаях разработки сложных моделей, предназначенных для проведения большого объема экспериментов, для решения этих задач используются моделирующие комплексы (системы).
К числу основных требований, предъявляемых к моделирующим системам, относятся следующие:
1) Рациональный состав функциональных возможностей, обеспечивающий баланс между высокой эффективностью разработки моделей, с одной стороны, и простотой овладения этими функциями пользователями системы, с другой стороны.
2) Открытость системы с точки зрения возможностей подключения других ресурсов (в частности, результаты моделирования, используемые для принятия управленческих решений, могут передаваться из моделирующей системы в базы данных экономической информационной системы, например, через интерфейс ODBC - если моделирование проводится в среде Windows - либо в процессе моделирования обращаться к данным, хранящимся в базе данных).
3) Оптимальный баланс между уровнем общности используемых в системе средств, обеспечивающих сокращение времени разработки модели, и универсальностью в смысле возможности использования системы для разработки моделей достаточно широкого класса.
4) Экономическая целесообразность, означающая, что эффект от применения системы к решению практических задач в течение периода ее промышленной эксплуатации существенно превысит затраты на создание системы, ее сопровождение и освоение пользователями.
С началом развития средств вычислительной техники и обусловленным им прогрессом теории и практики имитационного моделирования создано более 300 языков моделирования дискретных систем и процессов. Примером одной из наиболее старых систем моделирования является система GPSS, которая была разработана сотрудником компании IBM Джеффри Гордоном в 1961 году (он же был и создателем описанного выше событийного алгоритма). Система и по сей день остается в числе наиболее распространенных и в своей несколько усеченной версии доступна для свободного применения.
Другой распространенной в России системой является система Pilgrim, представляющая собой программный продукт, созданный на объектно-ориентированной основе и учитывающий основные достоинства ряда других моделирующих систем. К достоинствам системы следует отнести:
1) Возможность имитации в одной модели процессов, связанных с движением материальных, информационных и финансовых потоков;
2) Наличие развитой CASE-оболочки, позволяющей конструировать многоуровневые модели в режиме структурного системного анализа;
3) Наличие интерфейсов с базами данных;
4) Возможность для конечного пользователя моделей непосредственно анализировать результаты благодаря формализованной технологии создания функциональных окон наблюдения за моделью с помощью Visual C++, Delphi или других средств;
5) Возможность управления моделями непосредственно в процесс выполнения с помощью специальных окон диалога.
С помощью системы Pilgrim можно создавать дискретно-непрерывные модели. Разрабатываемые модели обладают свойством коллективного управления процессом моделирования. В текст модели можно вставлять блоки на языке C++. Различные версии этой системы работали на IBM-совместимых и DEC-совместимых компьютерах под операционными системами семейств Unix или Windows.
Система Pilgrim обладает свойством мобильности, т.е. переноса на любую другую платформу при наличии компилятора C++.
Поскольку выполняемый код модели в системе Pilgrim является результатом компиляции описания модели, то программные модели отличаются высоким быстродействием. Это позволяет эффективно их применять для решения задач оценивания, принятия управленческих решений и адаптивного выбора вариантов.
Полученный в результате компиляции объектный код можно встраивать в программные комплексы или применять на любом объекте, так как для запусков разработанных программных моделей средства системы Pilgrim не требуются.
Рассматриваемые далее подходы и методические приемы ориентированы на систему Pilgrim, однако в полной мере сохраняют свою общность и могут использоваться в других моделирующих системах.
Для построения моделей в системе Pilgrim используются следующие концептуальные и конструкционные элементы.
Структурной средой протекания всех моделируемых процессов, независимо от количества уровней структурного анализа, является ориентированный граф.
Представляет собой формальный запрос на какое-либо обслуживание. Транзакт в отличие от обычных заявок, которые рассматривались при анализе модели массового обслуживания в теме по стохастическим системам, имеет набор динамически изменяющихся свойств и параметров.
Транзакт является динамической единицей любой модели, работающей под управлением имитатора, и может выполнять следующие действия:
· порождать группы (семейства) других транзактов;
· поглощать другие транзакты конкретного семейства;
· захватывать ресурсы, использовать их в течение некоторого времени, а затем - освобождать;
· определять времена обслуживания, накапливать информацию о пройденном пути и иметь информацию о своем дальнейшем пути и о путях других транзактов.
К основным параметрам транзактов относятся:
· уникальный идентификатор транзакта;
· идентификатор (номер) семейства, к которому принадлежит транзакт;
· наборы различных ресурсов, которые транзакт может захватывать и использовать какое-то время;
· время жизни транзакта;
· приоритет - неотрицательное число; чем больше приоритет, тем приоритетнее транзакт (например, в очереди);
· параметры обслуживания в каком-либо обслуживающем устройстве (включая вероятностные характеристики).
Транзактами могут быть:
· требование на перечисление денег;
· заказ услуг в какой-либо компании;
· телеграмма, поступающая на узел коммутации сообщений;
· сигнал о загрязнении какого-либо пункта местности;
· приказ руководства;
· покупатель магазина;
· пассажир самолета;
· ожидающая анализа проба загрязнения почвы.
Пути перемещении транзактов по графу стохастической сети определяются логикой функционирования компонентов модели в узлах сети.
Узлы графа модели представляют собой центры обслуживания транзактов (но необязательно массового обслуживания). В узлах транзакты могут задерживаться, обслуживаться, порождать семейства новых транзактов, уничтожать другие транзакты. С точки зрения вычислительных процессов в каждом узле порождается независимый процесс. Вычислительные процессы выполняются параллельно и координируют друг друга. Они протекают в едином модельном времени, в одном пространстве, учитывают временную, пространственную и финансовую динамику. В системе Pilgrim имеется 17 типов узлов, реализующих специальные функции обслуживания.
Нумерация и присвоение имен узлам стохастической сети производится разработчиком модели. Транзакт всегда принадлежит одному из узлов графа и независимо от этого относится к определенной точке пространства или местности, координаты которой могут изменяться.
Каждый узел имеет графическое обозначение, функциональное наименование, произвольный уникальный номер и произвольное название. Пути следования транзактов обозначаются дугами - сплошными линиями со сплошной стрелкой на одном конце. Возможные воздействия одних узлов на другие узлы изображаются пунктирными линиями со стрелкой на одном конце.
Примерами узлов могут служить:
· счет бухгалтерского учета;
· бухгалтерия предприятия;
· производственный (ремонтный) участок;
· транспортное средство, которое перемещает ресурсы из одной точки пространства в другую;
· передвижная лаборатория;
· компьютерный центр коммутации сообщений (или пакетов сообщений);
· склад ресурсов.
Событием называется факт выхода из узла одного транзакта. События всегда происходят в определенные моменты времени. Они могут быть связаны и с точкой пространства. Интервалы между двумя соседними событиями в модели - это, как правило, случайные величины. Так, если в момент времени t произошло какое-то событие, а в момент времени t+d должно произойти ближайшее следующее (но не обязательно в этом же узле) и если в модель включены непрерывные компоненты, то очевидно, что передать управление таким компонентам модели можно только на время в пределах интервала (t, t+d).
Разработчик модели не может управлять событиями (например, из программы). Поэтому функция управления событиями отдана специальной управляющей программе - координатору, входящей в состав модели.
Независимо от своей природы ресурс в процессе моделирования может характеризоваться тремя параметрами: мощностью, остатком и дефицитом.
Мощность ресурса - это максимальное число ресурсных единиц, которые можно использовать для различных целей.
Остаток ресурса - число незанятых на данный момент единиц, которые можно использовать для удовлетворения транзактов.
Дефицит ресурса - количество единиц ресурса в суммарном запросе транзактов, стоящих в очереди к данному ресурсу.
При решении задач динамического управления ресурсами можно выделить три основных типа ресурсов: материальные, информационные и денежные.
Географическое, декартова плоскость (можно ввести и другие). Узлы, транзакты и ресурсы могут быть привязаны к точкам пространства и перемещаться в нем.
Примером графа модели в системе Pilgrim может служить граф модели рассмотренной ранее одноканальной СМО с неограниченной очередью (рис. 24):

Рис. 24. Граф модели одноканальной СМО
Граф модели включает следующие узлы (транзакты в имитационной модели означают запросы к системе массового обслуживания).
|
|
Узел ag (AG) представляет собой генератор транзактов имитационной модели. Транзакты генерируются по одному через промежутки времени, величина которых определяется по правилу, заданному пользователем через параметры узла. |
|
|
Узел Queue (Q) моделирует очередь транзактов. |
|
|
Узел Serv (S) имитирует прибор, или сервер, осуществляющий какое-либо обслуживание транзактов в течение модельного времени, отличного от нуля. С точки зрения имитационной модели обслуживание заключается в задержке транзакта на заданный промежуток времени. Сервер - это одно- или многоканальный обслуживающий прибор, работающий по правилам абсолютных приоритетов или без них и имеющий стек для «прерванных» транзактов (правило относительных приоритетов реализуется в узле типа Queue). Аналогично узлу ag время нахождения транзакта в узле (продолжительность обслуживания) определяется по правилу, заданному пользователем через параметры узла. |
|
|
Узел Term (T) представляет собой уничтожитель транзактов (терминатор). Он удаляет из программной модели входящие в него транзакты. Одновременно узел фиксирует время существования транзакта, начиная с момента выхода последнего из генератора. |
Для автоматизации составления описания модели и получения на его основе исходного текста программной модели в моделирующей системе Pigrim предусмотрен специальный конструктор Gem. На рис. 25 показано окно конструктора с построенным в его рабочей плоскости графом модели СМО.
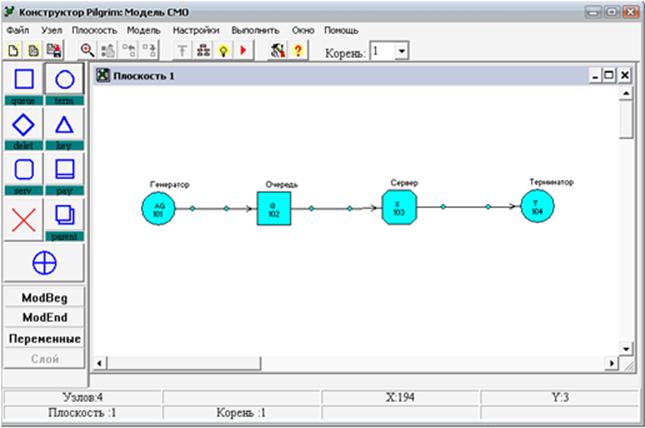
Рис. 25. Граф модели СМО на рабочей плоскости конструктора Gem
Рассмотрим основные возможности и правила работы с конструктором.
Результаты проектирования/корректировки модели.
Описание модели конструктор сохраняет в файле с расширением pgf (Pilgrim graf file), выполняя команду Сохранить (Сохранить как) меню Файл.
Для законченной версии модели разработчик может сгенерировать программный файл модели с расширением cpp, который будет далее скомпилирован в среде Visual C++ и вместе с подключенными библиотеками и ресурсами Pilgrim использован для сборки исполнительного модуля программной модели. Файл с исходным текстом программы создается командой Генерировать С++-файл меню Выполнить.
Установка параметров моделирования.
Задание основных параметров модели производится с помощью инструмента ModBeg (рис. 26):
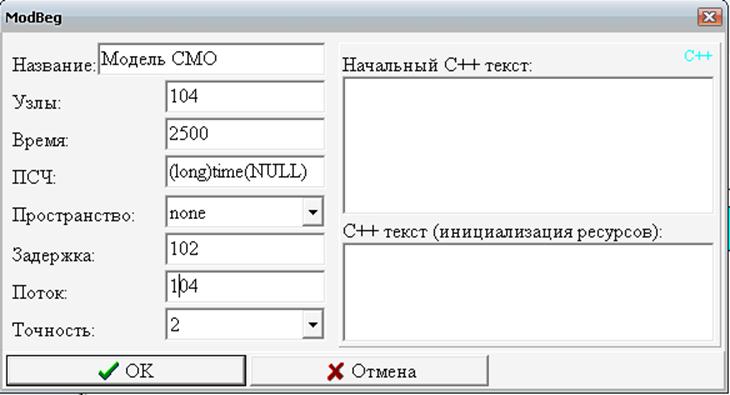
Рис. 26. Окно задания параметров моделирования
В строку Название вводится имя модели, которое будет указано в таблице результатов моделирования.
В строке Время указывается время моделирования.
В строке ПСЧ указывается начальное значение для генератора псевдослучайных чисел, необходимых для имитации случайных процесов. По умолчанию в качестве начального значения берется показание компьютерного таймера.
Строки Задержка и Поток предназначены для задания номеров контролируемых узлов: очереди (Queue) и терминатора (Term) соответственно. Для указанных узлов в процессе моделирования будут строиться графики времени задержки в узле типа Queue и динамики выходного потока в узле типа Term.
В правой верхней части окна записывается начальный текст на С++, если он необходим. Программный текст делится на две части: начальный текст используется для подключения внешних библиотек и настройки глобальных параметров; текст инициализации ресурсов подготавливает параметры конкретных узлов типов attach и send. Другие поля окна позволяют редактировать переменные, стандартные для оператора modbeg.
Параметры файла, содержащего результаты моделирования, задаются с помощью инструмента ModEnd (рис. 27):
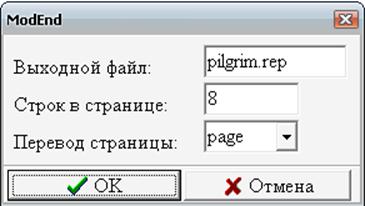
Рис. 27. Окно задания параметров файла-отчета
При определении новой переменной модели (рис. 28) обязательными параметрами в окне ввода (вызывается с помощью инструмента Переменные на панели инструментов) являются имя и тип, значение пользователь может задавать или не задавать по своему усмотрению.
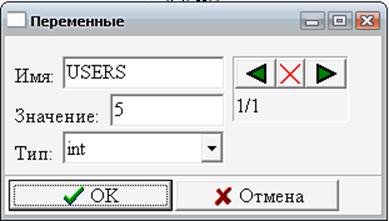
Рис. 28. Окно задания переменных модели
В процессе редактирования графа модели можно выполнять следующие действия:
· добавлять новые узлы;
· перемещать узлы в области построения;
· удалять существующие узлы;
· определять маршруты переходов транзактов.
Для редактирования графа модели в конструкторе используется технология «перетаскивания и бросания» объекта, обозначающего тип требуемого узла или действия, из панели инструментов в область построения графа. Панель инструментов в левой части окна редактора содержит значки, обозначающие узлы системы. Изображения узлов перетаскиваются при нажатой левой кнопке мыши. На панели представлены группы узлов, поэтому в отдельных случаях (в тех, когда на панели указан другой класс узла) для указания класса узла потребуется выполнить дополнительное действие. Задать класс можно:
1) Перетаскиванием графического символа какого-либо узла из группы на рабочую плоскость и последующим изменением свойства Класс узла (окно свойств может быть вызвано выбором опции Параметры контекстного меню, отображаемого нажатием правой клавиши мыши, или двойным щелчком левой кнопки по изображению узла). Например, узел term можно задать, поместив на рабочую плоскость узел ag и поменяв его класс со значения AG на значение Terminator.
2) Одним или несколькими нажатиями клавиши под значком узла на панели инструментов до момента появления узла нужного класса.
Узлы нумеруются автоматически (первая цифра номера означает номер плоскости, так как в системе Pilgrim есть возможность иерархического построения графа моделей.
Для удаления узла нужно:
·
захватить инструмент ![]() левой кнопкой мыши;
левой кнопкой мыши;
· не отпуская кнопку, поместить указатель мыши на удаляемый узел;
· подтвердить необходимость удаления.
Для проведения стрелки нужно:
·
захватить инструмент ![]() левой кнопкой мыши;
левой кнопкой мыши;
· не отпуская кнопку, поместить указатель мыши на узел-источник стрелки;
· отпустить кнопку, что будет означать привязку начала стрелки к данному узлу;
· поместить указатель мыши на узел-приемник стрелки и щелкнуть левой кнопкой мыши.
Для удаления стрелки нужно:
· войти в окно описания узла-источника стрелки;
· пометить мышкой соответствующий Выход из узла;
· нажать кнопку Удалить.
Номер узла присваивается конструктором при его создании. Обычно первые 100 номеров зарезервированы для узлов send - бухгалтерских счетов. Нумерация создаваемых узлов осуществляется последовательно, с номера 101. Смена номера узла возможна с помощью соседнего с номером диалогового поля, но не рекомендуется для узлов, созданных ранее.
Каждый узел модели характеризуется множеством параметров:
· типом;
· порядковым номером;
· именем;
· принадлежностью к плоскости;
· ссылками;
· условиями переходов;
· встроенным программным текстом;
· параметрами, определяемыми спецификой типа узла, такими, как закон - распределения для узла типа serv, приоритет для queue и т.п.
Для описания узла необходимо открыть окно его свойств (рис. 29).
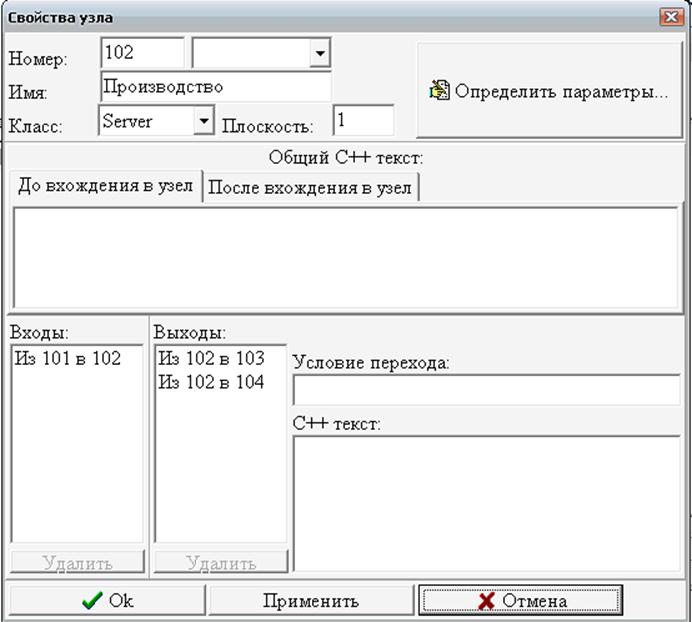
Рис. 29. Окно задания свйств узла
Для вызова окна необходимо дважды щелкнуть по изображению узла левой кнопкой мыши либо один раз щелкнуть по узлу правой кнопкой и после появления всплывающего меню выбрать в нем пункт Параметры узла.
Узел может содержать несколько ссылок на узлы, в которые может перейти транзакт из данного узла. Выбор маршрута должен осуществляться в соответствии с условиями, которые формулируются в правой нижней части окна определения параметров транзакта (поле Условие перехода). Для каждого из маршрутов выхода транзакта могут определяться действия, выполняемые после выхода, в виде операторов на языке С++.
Выбор исходящей ссылки осуществляется щелчком мыши в диалоговом поле Выходы. Любой вход и любой выход можно удалить, нажав кнопку Удалить под списком. На Рис. показан пример задания условий (для окна на рис. 29), при которых транзакт переходит из узла 102 в узел 103, и действий, выполняемых в этом случае.
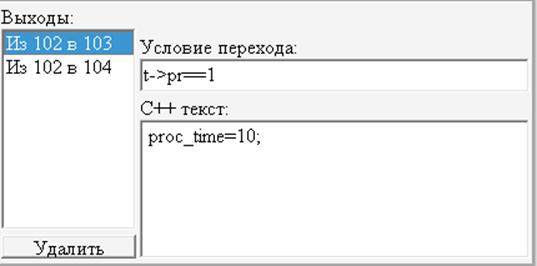
Рис. 30. Спецификация условий и действий
Панель Общий С++ текст позволяет включить в процедуру обработки узла произвольный текст на языке С++. Текст имеет две части: одна выполняется до выполнения узлового оператора, другая - после. До вхождения транзакта в узловой оператор могут формироваться значения параметров, необходимых для выполнения оператора, например, величина среднего времени обслуживания транзакта в узле serv. После выхода транзакта из узлового оператора могут стоять конструкции, предназначенные для управления логикой работы модели (сигнальные функции - см. далее) или осуществляющие сбор (накопление) статистики для подсчета итогов.
Поле Имя содержит имя узла, отображаемое на схеме и в таблице с результатами моделирования. Имена, назначаемые по умолчанию, можно (и целесообразно) изменять.
Значение поля Класс выбирается из списка, который состоит из типов узлов, имеющих одинаковый графический символ. Например, узел типа send можно сменить на attach (при этом изменяется набор и смысл параметров узла).
Нажатие кнопки Определить параметры приведет к появлению окна, вид которого зависит от типа узла. Так, для узла serv окно будет иметь вид, показанный на рис 31:
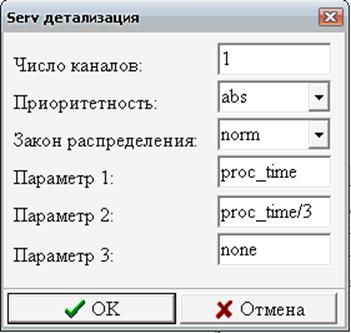
Рис. 31. Окно установки параметров узла
Смысл параметров Параметр 1, Параметр 2, Параметр 3 зависит от значения, указанного в поле ввода параметра Закон распределения. В частности, Параметр 1 для экспоненциального и нормального законов распределения представляет собой математическое ожидание (среднее), а Параметр 2 для нормального законов распределения - среднеквадратическое отклонение времени нахождения транзакта в узле.
Поле Плоскость показывает, к какой плоскости принадлежит узел, и доступно только для просмотра.
Построенная с помощью конструктора модель подвергается проверке. Предусмотрено два типа проверок:
· автоматическая в процессе построения модели (заведомо ложные действия блокируются);
· полная проверка графа (запускается командой меню).
Результат проверки графа выдается в окне в виде списка возможных и явных ошибок (рис. 32), не позволяющих сгенерировать программный Рilgrim-файл (к явным ошибкам относятся отсутствие выходов или входов узла и неопределенные вход/выход плоскости – см. далее).
Рис. 32. Окно сообщений об ошибках в графе модели
Проверка корректности графа производится автоматически в момент, непосредственно предшествующий генерации программного Рilgrim-файла, а также может быть вызвана явно указанием пункта Выполнить основного меню.
1. Для исследования стохастических систем применяется имитационное моделирование. Механизм машинной реализации этой методологии основан на агрегатном описании моделируемых процессов, при котором программным образом воспроизводится последовательность смен моделируемой системой своих состояний.
2. Эффективность применения подхода на основе имитационного моделирования к решению сложных задач можно значительно повысить путем использования моделирующих комплексов. Их применение позволяет значительно сократить затраты на создание модели проведение на ней машинных экспериментов.
3. Повысить эффективность и автоматизировать процессы создания и применения моделей в моделирующих комплексах можно путем построения концептуальной основы, позволяющей получать формализованное описание моделируемого объекта и генерировать на его основе программный код. Основными элементами описание модели в системе Pilgrim являются граф, транзакт, узел, ресурс, событие, пространство.
4. Использование стандарта для описания модели в моделирующих комплексах позволяет автоматически получать исходный текст программной модели с помощью специальных компонентов. В системе Pilgrim таким компонентом является конструктор моделей Gem.
1. Решение каких задач можно автоматизировать при помощи моделирующих комплексов?
2. Поясните на блок-схеме логическую последовательность действий по имитации работы одноканальной СМО с очередью.
3. Какие требования предъявляются к моделирующим комплексам?
4. Каковы основные достоинства моделирующей системы Pilgrim?
5. Что представляет собой модель в системе Pilgrim?
6. Что называется транзактом в модели системы Pilgrim?
7. Что такое узел в системе Pilgrim?
8. Какие узлы системы Pilgrim нужны для моделирования одноканальной системы массового обслуживания?
9. Что такое ресурс в системе Pilgrim?
10. Что является событием в модели системы Pilgrim?
1. Емельянов А.А., Власова Е.А., Дума Р.В. Имитационное моделирование экономических процессов / Под ред. А.А. Емельянова. – М.: Финансы и статистика, 2009. – 480 с.. Емельянова. – М.: Маркет ДС, 2010. – 464 с.
· познакомиться с технологией создания Pilgrim -модели;
· выяснить состав результатов моделирования;
· изучить правила выполнения основных этапов технологии создания и использования модели.
· понять назначение языковых средств системы Pilgrim;
· выяснить состав, структуру и форматы выходных параметров моделирования.
получите представление о:
· основных языковых средствах системы Pilgrim;
· структуре и форматах разделов программной Pilgrim-модели;
· составе узловых операторов модели;
будете знать:
· как прочитать текст программной модели на исходном языке;
· как внести изменения модель минуя этап описания ее графа;
· как собрать исполнительный модуль модели;
· как запустить модель;
· как прочитать результаты моделирования;
· семантику и синтаксис основных узлов.
1. Структура программной модели в системе Pilgrim.
2. Узловые операторы.
3. Текст программной модели СМО.
4. Сборка и запуск исполнительного модуля модели.
5. Результаты моделирования.
Все узлы имитационных моделей являются процессами в системе Pilgrim. Стохастическая сеть, в виде которой представляется модель, не является вычислительным алгоритмом. Попытки представить имитационную модель в виде набора алгоритмов приводят к написанию больших (и сложных) моделирующих программ. Такой подход называется алгоритмическим моделированием; он не всегда доступен прикладному специалисту, даже имеющему подготовку в области программирования.
Модель реальной системы может состоять из очень большого числа узлов. Поэтому нужны специальные языковые средства, не являющиеся языком программирования, которые бы позволили в лаконичном (по сравнению с текстом компьютерной программы) виде описать модель. Эти средства должны учитывать особенности узлов, жизненных циклов транзактов, условий прохождения транзактов по дугам, их размножения и гибели, а также функциональные особенности взаимодействия процессов, связанных с финансовыми, материальными и информационными ресурсами.
Набор языковых средств, предназначенных для описания имитационных моделей процессов, обеспечивает выполнение следующих задач:
1) Инициализацию объектов и структур данных при запуске программной модели.
2) Описание узлов с помощью общих операторов управления транзактами, событиями и узлами модели.
3) Функциональное описание процессов управления материальными и денежными ресурсами.
4) Управление переходами между слоями модели при многоуровневой декомпозиции.
5) Описание сигнальных управляющих функций.
Данные средства по форме записи являются функциями, через параметры которых реализуются синтаксические связи между объектами (узлами, транзактами, ресурсами и событиями) имитационной модели. Форма записи различных условий и условных действий соответствует языку C++.
Ниже представлен перечень основных разделов программного модуля на языке C++, на основе которого формируется исполнительный модуль для реализации модельных экспериментов (названия необязательных разделов заключены в квадратные скобки).
|
#include <Pilgrim.h> |
|
[Глобальные переменные и функции] |
|
forward |
|
{ |
|
[Локальные переменные модели] |
|
modbeg (p1,p2,p3,p4, p5,p6,p7,p8,p9) |
|
ag (p1,p2,p3,p4, p5,p6,p7,p8) ………………………… ag (p1,p2,p3,p4, p5,p6,p7,p8) |
|
[Сигнальные функции] |
|
network (p1,p2) |
|
{ |
|
Узел 1 …….. Узел N |
|
} |
|
modend (p1,p2,p3,p4) |
|
return 0; |
|
} |
#include <Pilgrim.h>
подключает моделирующую среду имитатора к модели.
Оператор modbeg (Р1, Р2, Р3, Р4, Р5, Р6, Р7, Р8, Р9) осуществляет первоначальную настройку моделирующих программ и инициализацию в памяти ЭВМ графа модели. Аргументы этой функции имеют следующий смысл:
Р1 – символическое имя узла: строка длиной до 14 символов (типа char);
Р2 – максимальный номер узла модели (типа int), причем 2≤p2≤mmax, где mmax – некоторое граничное значение, задаваемое при установке имитатора на ЭВМ (обычно mmax =1024);
Р3 – модельное время, в течение которого необходимо производить моделирование (типа float);
Р4 – произвольное целое число, используемое для настройки датчиков псевдослучайных величин (long). В каждом узле есть свой независимый датчик. В качестве этого числа полезно использовать значение таймера ЭВМ, обращение к которому имеет следующий вид p4=(long)time(NULL). В этом случае результаты разных прогонов модели будут разными, имеющими случайные отклонения. При отладке лучше использовать постоянную комбинацию цифр, например, p4=(long)2013456789.
Р5 – признак режима пространственной имитации (типа int); возможные значения:
· earth –поверхность Земли (сферические географические координаты широта и долгота);
· plane –декартова плоскость (прямоугольная система координат);
· cosmos –произвольное пространство (ответственность за правильность его представления возлагается на разработчика модели);
· none – если пространственная имитация в модели не используется.
Р6 – номер (типа int) одной из очередей (узел типа queue, attach или send), которую необходимо контролировать во времени для анализа динамики задержек в этой очереди с графическим отображением результатов.
Р7 – номер (типа int) одного из процессов (узла типа proc), который необходимо контролировать как в пространстве, так и во времени с графическим отображением результатов. Если нет необходимости в графической интерпретации, то указывается none.
Р8 – номер (типа int) терминатора (узел типа term), на входе которого необходимо наблюдать интенсивность потока транзактов во время моделирования. Если такой необходимости нет, то указывается none.
Р9 – точность (типа int). Если Р9=1..6, то имитатор будет использовать от 1 до 6 знаков после запятой при выводе результатов; если Р9=none, то результаты будут округляться до целых значений.
Оператор network (Р1, Р2) представляет собой координатор процессов модели. Он осуществляет диспетчеризацию транзактов в узлах модели, планирует события в едином модельном времени и активизирует дискретные или непрерывные компоненты модели, имитирующие внешнюю среду. Аргументы Р1 и Р2- это имена (адреса) соответствующих программных функций моделирования внешней среды, производящих интегрирование, решение разностных уравнений, вычисление по формулам и т.д. Функции float Р1 (d) и float Р2 (d), если они необходимы, пишутся пользователем. Если процессы Р1 (d) и Р2 (d) не моделируются, то в качестве Р1 и Р2 записывается dummy.
Оператор modend (Р1, Р2, Р3, Р4) выполняется по окончании моделирования. Он позволяет просмотреть на экране монитора графические результаты и выводит итоговые результаты в файл-отчет. Аргументами оператора являются:
Р1 – символическое имя файла-отчета (сhar);
Р2 – номер первой страницы отчета (int);
Р3 – число строк на каждой странице (int);
Р4 – флаг символа перевода страницы в файле-отчете; возможные значения:
· page символ ставится;
· none символ не ставится.
Узел в тексте программы состоит из шести компонентов (необязательные компоненты заключены в квадратные скобки):
|
top(i): |
|
[Описание условий] |
|
Узловой оператор |
|
[Сигнальные функции] |
|
[Блок операторов С++] |
|
place; |
Описание узла начинается с метки-функции top (i), где i - номер этого узла (записывается с двоеточием).
Начиная с метки top(i) транзакт проходит все операторы узла i без временных задержек и попадает в оператор place, где находится до тех пор, пока не появятся условия для перехода в следующий узел.
В некоторых узлах одновременно могут находиться несколько транзактов и все они содержатся в операторе place.
Не следует путать поток транзактов в модели с потоком управлений в обычной программе. Задержка транзакта в place - это и есть время пребывания в узле.
После метки top(i) можно анализировать условия продвижения транзактов по графу модели, при этом используются операторы if или switch. Для динамического изменения направления движения транзактов, законов распределения, значений времени обслуживания и других параметров можно использовать операцию присваивания.
Например, если в узле 3 нужно изменить значение переменной b в зависимости от значения переменной а, то следует записать:
top(3): if (a < 0)
b =4;
else
b =3*а+5;
key («Переключатель», b);
place;
где
key - оператор, определяющий узел типа клапан.
Основным обязательным оператором, который стоит после двоеточия метки-функции, является оператор определения типа узла (узловой оператор). Этот оператор имеет условное наименование, совпадающее с типом узла. Сводка и краткая характеристика всех узлов, имеющихся в системе Pilgrim приводится в Приложении.
В качестве узловых операторов могут использоваться все типы узлов кроме ag и parent.
После узлового оператора могут размещаться сигнальные функции и операторы С++, образуя конструкцию:
clcode
{
<операторы>
}
Эти операторы могут задавать различные действия по управлению работой модели, например, по сбору статистики или трассировке, которые будут обсуждаться далее.
Последним оператором узла является оператор place;
Описание узла иногда состоит только из метки-функции top(i), узлового оператора и оператора place. Например:
top(i): key ( «Переключатель», j );
place;
На рис. 33 показан текст программы, который был сгенерирован на основании описания модели в конструкторе Gem для ранее рассмотренной модели СМО.
#include <Pilgrim.h>
forward
{
int fw;
modbeg («СМО», 105, 2500, (long)time(NULL), none, 102, none,104, 2);
ag («Генератор», 101, none, expo, 12.0, none, none, 102);
network (dummy, dummy)
{
top (102):
queue(«Очередь», none, 103);
place;
top (103):
serv(«Сервер», 1, none, expo, 9.0, none, none, 104);
place;
top (104):
term(«Терминатор 104»);
place;
fault (123);
}
modend («pilgrim.rep», 1, 8, page);
return 0;
}
Рис. 33. Исходный текст программной модели СМО
Для лучшего понимания сгенерированного текста приведем описание присутствующих в программе узловых операторов.
Функция ag (Р1, Р2, Р3, Р4, Р5, Р6, Р7, Р8) описывает узел, порождающий в соответствии с заданным правилом в процессе моделирования транзакты и направляющий их в указанную точку (узел) модели.
Функция имеет следующие параметры:
Р1- символическое имя узла (строка длиной до 14 символов типа char);.
Р2- номер узла-генератора (типа int);
Р3- число (типа int в диапазоне 1-32767), обозначающее приоритет, который присваивается сгенерированному транзакту, или none, если приоритет не присваивается;
Р4- тип функции распределения интервала времени между генерируемыми транзактами, имеющий значения:
· norm - нормальное распределение;
· unif - равномерное распределение;
· expo - экспоненциальное распределение;
· erln - обобщенное распределение Эрланга;
· beta - треугольное распределение;
· none -если интервал обслуживания является детерминированной величиной.
Р5- величина (типа float), зависящая от типа функции распределения Р4:
· математическое ожидание интервала времени обслуживания транзакта (при Р4= norm, unif, expo);
· математическое ожидание одного слагаемого этого интервала (при Р4= erln);
· минимальное значение интервала (при Р4= beta);
· постоянная величина этого интервала (при Р4= попе).
Р6 – величина (типа float), зависящая от типа функции распределения Р4:
· среднеквадратичное отклонение времени обслуживания (Р4= norm);
· максимальное отклонение от среднего времени обслуживания (Р4= unif);
· значение zero (Р4 = expo, none);
· число слагаемых, распределенных по экспоненциальному закону и входящих в случайный интервал обслуживания (если Р4= erln, то Р6 > 0);
· наиболее вероятное значение интервала времени обслуживания транзакта (при Р4=beta).
Р7- величина (типа float), зависящая от типа функции распределения Р4:
· максимально возможное значение интервала времени обслуживания транзакта (Р4=beta);
· значение zero (Р4= norm, unif, expo, erln, ш).
Р8- номер узла (типа int), в который поступает сгенерированный транзакт (узел-приемник).
Функция queue (Р1,Р2,Р3) описывает узел, моделирующий очередь транзактов.
Функция имеет следующие параметры.
Р1 – символическое имя узла (строка длиной до 14 символов типа char);
Р2 – тип организации очереди (типа int):
Р2 – ргtу, если очередь с приоритетами,
Р2 – none, если очередь без приоритетов.
Р3 – номер узла (типа int), в который переходит транзакт из очереди (узел-приемник).
Если в качестве параметра Р6 оператора modbeg поставить номер узла-очереди, то можно автоматически получать график изменения среднего времени нахождения транзактов в этой очереди.
Функция serv (Р1, Р2, Р3, Р4, Р5, Р6, Р7, Р8) описывает узел, имитирующий одно- или многоканальный обслуживающий прибор. Может использовать или не использовать дисциплину обслуживания на основе абсолютных приоритетов. Имеет стек для хранения прерванных транзактов.
Функция имеет следующие параметры:
Р1- символическое имя узла (строка длиной до 14 символов типа char);
Р2- число обслуживающих каналов, l < Р2<32767;
Р3- дисциплина обслуживания; возможные значения:
· abs, используется приоритетная дисциплина, с прерыванием обслуживания менее приоритетного транзакта более приоритетным; при этом после ухода приоритетного транзакта возможно одно из двух:
· дообслуживание прерванного транзакта с прерванного места;
· возобновление обслуживания прерванного транзакта заново.
· none, используется бесприоритетная дисциплина.
Р4 - тип функции распределения интервала времени обслуживания транзакта в канале узла, возможные значения:
· norm - нормальное распределение;
· unif - равномерное распределение;
· expo - экспоненциальное распределение;
· erln - обобщенное распределение Эрланга;
· beta - треугольное распределение;
· none -если интервал обслуживания является детерминированной величиной.
Р5- величина (типа float), зависящая от типа функции распределения:
· математическое ожидание интервала времени обслуживания транзакта (при Р4= norm, unif, expo);
· математическое ожидание одного слагаемого этого интервала (при Р4= erln);
· минимальное значение интервала (при Р4= beta);
· постоянная величина этого интервала (при Р4= none).
Р6 – величина (типа float), зависящая от типа функции распределения:
· среднеквадратичное отклонение времени обслуживания (Р4= norm);
· максимальное отклонение от среднего времени обслуживания (Р4= unif);
· значение zero (Р4 = expo, none);
· число слагаемых, распределенных по экспоненциальному закону и входящих в случайный интервал обслуживания (если Р4= erln, то Р6 > 0);
· наиболее вероятное значение интервала времени обслуживания транзакта (при Р4=beta).
Р7- величина (типа float), зависящая от типа функции распределения:
· максимально возможное значение интервала времени обслуживания транзакта (Р4=beta);
· значение zero (Р4= norm, unif, expo, erln, none).
Р8- номер узла (типа int), в который передается обслуженный транзакт (узел-приемник).
Функция term (Р1) описывает узел-терминатор, который удаляет из модели входящий в него транзакт и фиксирует время его существования начиная с момента выхода этого транзакта из генератора.
Функция имеет один параметр:
Р1- символическое имя узла (строка длиной до 14 символов типа char).
Если в качестве параметра Р8 подставить в modbeg номер узла-терминатора, то можно автоматически получать график потока транзактов, поступающих на его вход.
Сгенерированный в результате описания модели файл с исходным текстом (<имя модели>.cpp) используется в качестве основы для получения работающей программы. Для этого необходимо выполнить следующую последовательность шагов.
1) Создать на жестком диске рабочую папку для будущего проекта.
2) Перенести в рабочую папку файл модели <имя модели>.cpp.
3) Открыть приложение Microsoft Visual С++.
4) Создать проект:
· File à Newà Projects à Win32 Application.
·
В окне Locaton посредством кнопки ![]() (Browse) указать
путь к файлу модели <модель>.cpp.
(Browse) указать
путь к файлу модели <модель>.cpp.
· В окне Project name указать имя проекта (латинскими буквами) и нажать кнопку OK.
· В открывшемся окне оставить неизменными установку по умолчанию для типа проекта (Empty application) и нажать кнопку OK.
5) Внести в проект файлы, необходимые для построения объектного кода модели (в таблице указаны папки, в которых обычно хранятся файлы):
|
Файл |
Папка |
Примечание |
|
Comctl32.lib |
Visual Studio/VC98/Lib |
Стандартная папка С++ |
|
Pilgrim.lib |
Visual Studio/VC98/Lib |
Стандартная папка С++ |
|
Pilgrim.res |
Visual Studio/VC98/ Projects |
Стандартная папка С++ |
|
<имя модели>.cpp |
папка с файлом исходного текста программной модели |
Должно соответствовать имени проекта, указанного в окне Location (файл модели); |
Вставка выполняется
командой Add Files To Folder / Add Files To Project контекстного меню, вызываемого правым щелчком мыши
после установки курсора на имя проекта (предварительно должна быть выбрана
вкладка ![]() в окне проектов).
в окне проектов).
6) Построить исполняемый файл модели.
· Выполняется одним из следующих способов:
o Build à Rebuild All главного меню Visual Studio.
o Нажатием функциональной клавиши F7.
o Нажатием значка ![]() панели
инструментов.
панели
инструментов.
Если в окне отчета о процессе построения появится сообщение 0 errors, можно запустить программную модель с помощью одного из следующих способов:
· Build à Execute ModelPro.exe.
· Нажатием комбинации функциональных клавиш Ctrl + F5.
·
Нажатием значка ![]() панели инструментов.
панели инструментов.
Установка параметров запуска модели и сам запуск производятся с помощью окна запуска. В частности, если требуется наблюдать график задержки по выбранной при построении графа модели очереди в динамике, то перед запуском программной модели нужно выбрать в меню Результаты пункт Динамика задержек в очереди (рис. 34Рис.).
Рис. 34. Задание динамического отображения очереди
Можно также выбрать режим динамического построения графика потока в транзактов в терминаторе (меню Результаты пункт Динамика потока).
После установки всех необходимых значений параметров в меню Моделирование нужно выбрать пункт Запуск модели (рис. 35).
Рис. 35. Запуск имитационной модели
Из общего меню модельного окна осуществляется также управление режимами трассировки, которая может помочь в отладке модели. В частности, имеется возможность (рис. 35):
· выйти в режим трассировки после наступления конкретного события;
· перейти в трассировку, если какой-то транзакт входит в определенный - узел или выходит из него;
· отслеживать путь определенного транзакта по графу модели;
· выйти в режим трассировки по показанию модельного таймера.
Основные результаты запуска программной модели помещаются в таблицу, которая содержится в файле с параметрами задаваемыми оператором modend. На рис. 36 приводится пример таблицы с результатами моделирования для модели СМО:
|
НАЗВАНИЕ МОДЕЛИ: |
СМО |
||||||||||
|
ВРЕМЯ МОДЕЛИРОВАНИЯ: |
15029.83 |
Лист: 1 |
|||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
№ узла |
Наименование узла |
Тип узла |
Точка |
Загрузка(%=), Путь(км) |
M [t] среднее время |
C [t] квадрат коэф.вар. |
Счетчик входов и hold |
Кол. кан. |
Оcт. тр. |
Состояние узла в этот момент |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
101 |
Генератор |
ag |
- |
- |
12.20 |
0.95 |
1229 |
1 |
1 |
открыт |
|
|
102 |
Очередь |
queue |
- |
- |
23.89 |
1.36 |
1229 |
1 |
1 |
открыт |
|
|
103 |
Сервер |
serv |
- |
%= 73.0 |
8.94 |
0.91 |
1228 |
1 |
0 |
открыт |
|
|
104 |
Терминатор |
term |
- |
- |
32.82 |
0.77 |
1228 |
0 |
0 |
открыт |
|
Рис. 36. Результаты моделирования для модели СМО
Строки таблицы представляют собой узлы модели, а столбцы – входные и выходные её параметры. В столбцах записываются:
|
№ узла |
Номер узла модели. |
|
Наименование |
Имя узла модели. |
|
Тип узла |
Тип узла. |
|
Точка |
Номер последней точки пространства, в которой находится узел типа creat, delet или proc на момент окончания моделирования. |
|
Загрузка (%), Путь (км) |
Для узлов типа serv или proc - коэффициент использования транзактами типа в процентах. Для узла типа key – доля времени пребывания в закрытом состоянии; Если производятся пространственные перемещения узлов типа proc, creat или delet, то подсчитывается пройденный путь. Для пространства типа GEO путь считается в километрах. |
|
М[t] среднее время |
Среднее значение времени задержки транзакта в узле или иной интервал времени, зависящий от типа узла: · для serv - это среднее время пребывания в узле (оно может быть больше времени обслуживания у неприоритетных транзактов при рз=аbs, т.е. при наличии приоритетных транзактов и правила абсолютных приоритетов); · для queue - среднее время задержки в очереди; · для ag - среднее время между двумя сгенерированными транзактами; · для term или delet - среднее время существования транзакта; · для key - среднее время пребывания в закрытом состоянии; · для creat и dynam - всегда нулевое значение; · для proc при p4=none, p4=поrm, p4=ехро или p4=unif - среднее время пребывания в узле (оно может быть больше времени обслуживания транзакта при переводе узла в пассивное состояние); · для proc при p4=earth, p4=plane или p4=cosmos -суммарное время пребывания транзакта в узлах dynam и proc с учетом возможных возвратов транзактов из proc в dynam. |
|
C2[t] квадрат коэф.вариации |
Отношение дисперсии временного интервала к квадрату его среднего значения. |
|
Счетчик входов и hold |
Число транзактов: · прошедших через узел; · сгенерированных транзактов (для ag или creat); · уничтоженных (для term или delet); · выполнивших операцию hold из другого узла в отношении узла key. |
|
Кол.каналов |
Число каналов в узле. |
|
Ост.тр. |
Количество транзактов, которые остались в узле на момент завершения моделирования. |
|
Состояние узла в этот момент |
Состояние узла в момент окончания прогона модели: · открыт/закрыт для входа очередного транзакта, активен/пассивен (proc); · положительное (денежная сумма с буквой S) /отрицательное (денежная сумма с буквой D) сальдо (send); · остаток (денежная сумма с буквой S) / дефицит (сумма с буквой D) ресурса (attach) ; · количество переходов транзактов на нижние слои-уровни модели (pay, rent). |
После окончания процесса моделирования можно посмотреть график, а также выходные параметры всех узлов модели (также с помощью меню Результаты).
Пример отображения графика, построенного в процессе имитации, показан на рис. 37, на котором синим цветом показано среднее время задержки в очереди за все время моделирования.
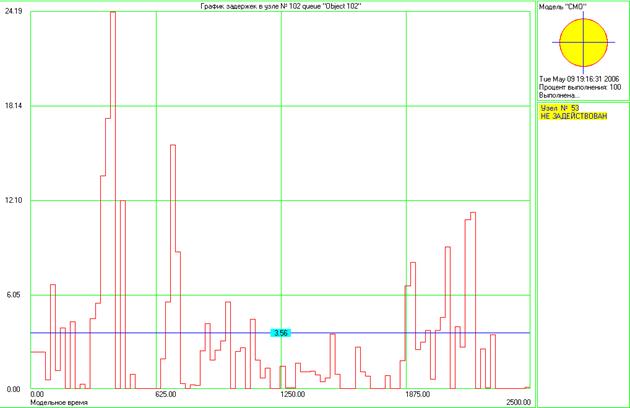
Рис. 37. Окно результатов запуска модели
Если после запуска модели требуется внести в нее какие-либо изменения, то перед очередным построением исполняемого файла необходимо закрыть окно модели.
Изменения можно вносить, минуя стадию создания с помощью конструктора файла .pgf непосредственно в файл .cpp,. Следует иметь в виду, однако, что эти изменения не будут отражены в файле .pgf.
1. Имитационные модели сложных систем могут содержать много узлов со сложными взаимосвязями между ними и сложной логикой протекания процессов. Для описания этих объектов и свойств оригинала в моделирующих комплексах применяются высокоуровневые средства, позволяющие создавать модель прикладным специалистам и не требующих специальных знаний в области программирования.
2. Вместе с тем, эффективность работ по созданию и последующей модификации программной модели можно существенно повысить в случае, когда разработчику предоставлена возможность внесения изменений непосредственно в исходный текст программной модели. В моделирующих системах типа системы Pilgrim структура программного текста стандартизована и содержится в описании системы, обеспечивая легкую модификацию и исправления.
3. Основные конструкции языка описания моделей в системе Pilgrim имеют унифицированный формат. Настройку моделей можно осуществлять заданием значений параметров узловых операторов и внесением логических конструкций в виде операторов языка С++ или Pascal, обеспечивающих маршрутизацию и управление перемещением транзактов.
4. В моделирующих комплексах типа Pilgrim модель представляет собой скомпилированный модуль. Для этого необходимо произвести сборку исполнительного модуля, которая в системе реализуется стандартной процедурой в среде пакета Visual Studio с включением в проект необходимых компонентов (модулей) системы Pilgrim.
5. Конечной целью имитационного моделирования является получение выходных данных. Моделирующие комплексы включают в себя средства для сбора, обработки и вывода стандартной набора параметров, которые в случае системы Pilgrim имеют специфицированный формат и выводятся в файл с отчетом о результатах моделирования.
1. Какие взаимосвязанные задачи реализуют языковые средства моделирующих комплексов?
2. Из каких основных разделов состоит программная модель системы Pilgrim на исходном языке?
3. Какую функцию выполняет предложение #include <Pilgrim.h>?
4. Каково назначение оператора modbeg?
5. Каково назначение оператора modend?
6. Как можно пронаблюдать в динамике задержки в узлах типа queue?
7. Как можно пронаблюдать в динамике задержки в узлах типа term?
8. Как запустить процесс имитации?
1. Емельянов А.А., Власова Е.А., Дума Р.В. Имитационное моделирование экономических процессов / Под ред. А.А. Емельянова. – М.: Финансы и статистика, 2009. – 480 с.
· познакомиться с понятием и назначением CASE-систем, применяемым в имитационном моделировании;
· получить представление о концепциях и технологии создания модели в среде конструктора Gem.
· познакомиться с концепцией CASE-систем;
· выяснить назначение и функции CASE-систем, применяемых для моделирования процессов и систем;
· познакомиться с концепциями конструктора Gem моделирующего комплекса Pilgrim.
получите представление о:
· функциональных возможностях конструктора Gem;
· особенностях пользовательского интерфейса конструктора Gem;
· способах настройки и модификации программного модуля модели;
будете знать:
· структуру текста исходного модуля программной модели;
· как строится работа в среде конструктора Gem;
· как задаются параметры модели;
· как описываются узлы на графе модели, параметры узлов и связи между узлами;
· из чего состоит результат прогона модели и какова его структура.
1. Создание многослойных моделей.
2. Использование узла parent.
3. Использование узлов pay, rent, down.
4. Многослойная модель бизнес-процесса.
Для создания имитационной модели в отсутствие вспомогательных средств разработчику нужно написать программный код, использующий языковые средства системы моделирования Pilgrim. Модель имеет стандартную структуру. Внутри текста модели содержатся обращения к функциям Pilgrim, но может быть и произвольный C++ код. Текст Pilgrim-модели обрабатывается препроцессором и стандартным компилятором C++ (Microsoft, Borland и др.). При этом требуется:
· знать элементы языка C++;
· представлять структуру программы, использующей библиотеку Pilgrim;
· знать синтаксис и семантику функций описания узлов и их параметров;
· находить и исправлять возможные ошибки в указании параметров (включая ошибки синтаксически верных конструкций, но нарушающие правила модели, что может проявиться в неверных результатах работы модели);
· преодолевать сложность составления моделей с большим числом узлов и нетривиальной логикой.
Конструктор имитационных Pilgrim-моделей Gem позволяет автоматизировать процесс создания модельного графа и автоматически генерировать код Pilgrim-программы. Тем самым отмеченные выше проблемы значительно упрощаются или снимаются вовсе. При использовании конструктора обеспечиваются:
· автоматическая генерация программного кода, что позволяет пользователю не задумываться о структуре и синтаксисе программы, уделяя все внимание структуре и параметрам самой модели и ее узлов;
· генерация функций описания узлов конструктором, что исключает ошибки, связанные с неправильной последовательностью указания позиционных параметров или пропуском некоторых из них;
· блокировка заведомо неверных действий пользователя, а также вывод предупреждений о возможных ошибках;
· поддержка разработки иерархических моделей, что может быть очень удобно при выполнении моделей с большим количеством узлов.
Широко применяемые при создании и использовании имитационных моделей CASE-средства (Computer Aided Software Engineering), к которым по своему типу и назначению относится конструктор Gem, активно используют методологию структурного анализа, предусматривающую наглядное и эффективное проектирование системы путем выделения ее составляющих и их последовательного рассмотрения. Описание системы начинается с общего обзора и выделения основных ее компонентов или процессов. Сначала создается первый уровень или слой, на котором отображаются выделенные процессы и их взаимосвязи. Далее для ряда процессов может быть проведена детализация, в свою очередь, выделяющая новые процессы в их структуре. Так, последовательным усложнением описания объекта и его процессов разработчик достигает необходимой детализации. Глубина детализации определяется как необходимой точностью, так и набором исходных данных. В процессе структурного анализа выявляется иерархическая структура модели.
С помощью конструктора Gem системы Pilgrim можно строить многоуровневые модели, организуя иерархию плоскостей построения модели. Иерархические модели устроены следующим образом: верхний уровень модели содержит ряд узлов, среди которых есть такие, которые детализируются на нижних уровнях. При этом, создавая детализирующий уровень, пользователь вновь может поместить на нее узлы, которые могут быть детализированы на нижележащих уровнях. Таким образом, граф модели примет иерархическую структуру. Число уровней вложенности конструктором не ограничено, т.е. пользователь может сколько угодно подробно детализировать и обобщать процессы модели.
Итак, процесс построения графа имитационной модели сопровождается структурным анализом исследуемого процесса. При структурном анализе возникает задача перехода между слоями: нижние слои модели содержат декомпозицию узлов, расположенных выше. Декомпозиция - это детализация одного узла с помощью совокупности других узлов.
Существуют четыре разновидности декомпозиции процессов:
1) общий случай декомпозиции сложного процесса с помощью узлов типа down;
2) декомпозиция процессов перечисления денег (платежей, бухгалтерских проводок и др.) с помощью узлов типа pay;
3) декомпозиция процессов выделения ресурсов с помощью узлов типа rent;
4) абстрактное объединение группы процессов в один псевдопроцесс с помощью виртуального (мнимого, не существующего в реальности) узла parent без образования нового узла.
Обратим внимание на то, что представленный методологический прием аналогичен методологическому приему, применяемому для построения функциональных моделей в процессе проведения системного анализа. Вместе с тем, важно понимать, что цель создания функциональных моделей отлична от целей создания имитационных моделей. Функциональная модель показывает, каким образом выходные элементы системы получаются из входных без рассмотрения логики преобразований. Модель создается, в первую очередь, для выявления основных подсистем (функций) рассматриваемого объекта и состоит из набора диаграмм потока данных.
В противоположность функциональной модели имитационная модель отображает все существенные действия в процессе их выполнения и создается для изучения поведения исследуемого объекта и параметров его функционирования.
При создании новой модели пользователь начинает работу с корневого уровня, поэтому некоторые процессы модели с целью дальнейшей детализации могут быть представлены в общем виде. Для выполнения структурной декомпозиции в системе Pilgrim определяется особый тип узла parent, использующийся исключительно как средство создания наглядных многоуровневых моделей. Узел типа parent содержит ссылку на плоскость, его детализирующую, т.е. используется для описания процессов, которые можно рассмотреть на отдельной плоскости. Узел parent не выполняет никаких действий по обработке транзакта и при генерации программного кода просто заменяется своей декомпозицией, т.е. порождаемым им слоем.
Например, если пользователь создал узел типа parent с номером 4, то в программном файле узел с таким номером сгенерирован не будет. С точки зрения генератора программного файла узел parent представляет собой маршрутизатор, который может иметь любое количество входов, ссылку на детализирующий уровень и единственный выход. На рис. 38 в плоскости 1 имеется последовательность узлов Клапан 101àДействие 102àОчередь 103.
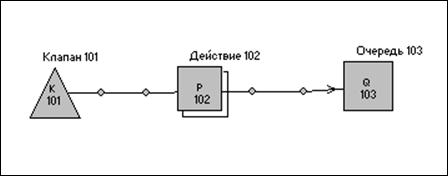
Рис. 38. Использование узла parent
Узел Действие 102 является узлом типа parent и содержит детализирующую плоскость с цепочкой Очередь 104 à Сервер 105 (рис. 39):
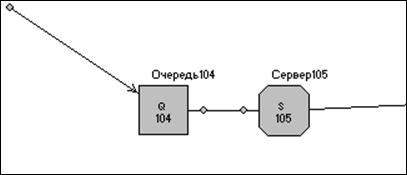
Рис. 39. Узлы на детализирующей плоскости
В этой плоскости стрелка, направленная из левого верхнего угла экрана в узел Очередь 104, обозначает, что этот узел является входом на плоскость, а стрелка из узла Сервер 105 в правый верхний угол - выходом с плоскости. При генерации программного файла получим следующую цепочку:
Клапан 101 à Очередь 104 à Сервер 105 à Очередь 103,
т. е. узел Действие 102 является лишь средством реализации (виртуальным узлом) и будет обработан генератором как узел Pilgrim.
Иногда при построении модели может возникнуть необходимость выделения некоторых типовых действий по обработке данных. Это могут быть запросы на выполнение бухгалтерской проводки, требования выделения моделируемого ресурса или какие-либо другие действия. При возникновении такой задачи удобно обозначить подпрограммы, обращение к которым было бы возможно из любого места модели. Для этого используются узлы типа pay, rent, down. Такие узлы, так же как и parent, содержат переход на более низкий уровень модели, однако имеют несколько иной механизм действия и область применения. Если с помощью узла типа parent можно создавать иерархические модели, имеющие на любой сколько угодно глубоко вложенной плоскости новые узлы parent, то с помощью узлов типа pay, rent, down возможно лишь реализовать подпрограммы на двух слоях модели и невозможно построить общую иерархию уровней.
Рассмотрим принцип работы таких узлов на примере узла pay. На плоскости 1 находится узел типа pay, содержащий обращение к подпрограмме, расположенной в плоскости 2 (рис. 40):
Входом плоскости 2 является узел с названием «Р/счет», а выходом - узел с именем «Бухгалтерия». При генерации программного файла в узле «Бухгалтерия» в качестве параметра, определяющего номер следующего узла, на который переходит транзакт, будет указано не конкретное значение, а специальный параметр транзакта updown. При этом предполагается, что каждый транзакт, попадающий в выходной узел плоскости, содержит в параметре updown номер узла, на который следует выполнить переход. Параметр транзакта updown инициализируется в узле типа pay, т.е. в данном случае в узле с названием «Плата поставщику».
Аналогичным образом реализуется переход на подпрограмму с использованием узлов типа rent и down. Они также инициализируют переменную транзакта updown. Таким образом, использовать узлы типа pay, rent и down для реализации иерархических моделей нельзя: на уровне подпрограммы для узла одного из этих типов нельзя размещать никакой из узлов типа pay, rent, down, поскольку каждый из этих узлов заново выполнит инициализацию параметра updown. Т.е., значение updown, установленное уровнем выше, заменится, организуя циклическую ссылку, что приведет к семантической ошибке.
Чтобы защитить пользователя от совершения таких ошибок, конструктор не позволяет создавать в текущей плоскости узлы типа pay, rent, down, если управление передано с более высокого уровня через узел перечисленного типа. Однако узлы обращения к подпрограмме имеют одно важное преимущество перед узлом parent, а именно: транзакт сам «помнит», куда ему необходимо вернуться. Поэтому из нескольких узлов или слоев можно обращаться к общей плоскости, содержащей детальное выполнение типового действия.
Предположим, что в последнем примере имеется некоторая организация, имеющая собственный расчетный счет и выполняющая ряд операций по перечислению средств; часть операций необходимо смоделировать. В плоскости 2 создана подпрограмма «Плата поставщику», выполняющая бухгалтерскую проводку по перечислению средств со счета фирмы. Если возникает необходимость смоделировать аналогичную ситуацию с перечислением средств (например, возврат кредита), то можно создать новый узел типа pay и указать ему в качестве подпрограммы плоскость 2.
В процессе работы с конструктором, при создании нового узла обращения к подпрограмме, появляется диалоговое окно с просьбой указать номер плоскости, на которой должна размещаться подпрограмма. По умолчанию это номер новой пустой плоскости, однако, пользователь самостоятельно может задать номер уже существующей плоскости.
Иногда в модели можно выделить ряд процессов, независимых на уровне транзактов, но пересекающихся на уровне моделируемых ресурсов. Например, это может быть моделирование процесса производства с участием нескольких независимых торговых компаний, приобретающих товар у производителя и имеющих свой финансовый резерв и рынок сбыта. Тогда можно выделить как независимые процессы торговых компаний и процесс функционирования производителя. Для разработчика модели неудобно располагать в одной корневой плоскости несколько параллельных процессов, поэтому конструктор предоставляет возможность содержать несколько корневых плоскостей с целью размещения в них непересекающихся на уровне транзактов процессов.
Проиллюстрируем применение описанного механизма на примере модели функционирования производственного предприятия. Пример является также хорошей иллюстрацией другого уже отмеченного ранее достоинства системы Pilgrim – возможности имитации протекания материальных, финансовых и информационных потоков в рамках одной и той же модели.
Моделируемый объект (небольшое предприятие) занимается выпуском товара малыми партиями, размер которых известен. Произведенная продукция реализуется на рынке, количество единиц реализуемой на рынке продукции в одной партии является случайной величиной, распределенной по равномерному закону.
Структурная схема бизнес-процесса содержит три слоя. На двух из них представлены независимо протекающие процессы производства (рис. 41).
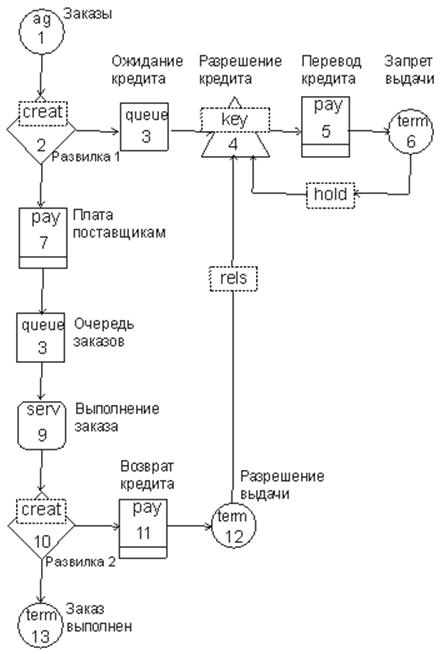
Рис. 41. Модельный граф процесса производства
и сбыта (рис. 42)
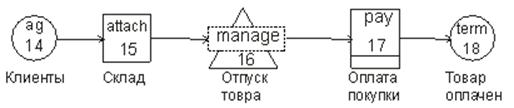
Рис. 42. Модельный граф процесса сбыта
продукции предприятия. Независимость протекания процессов означает, что транзакты могут перемещаться только внутри каждого из фрагментов графа модели на каждом слое. Взаимодействие процессов осуществляется только через ресурсы: материальные (в виде готовой продукции) и денежные (в основном через расчетный счет предприятия).
На третьем слое имитируется выполнение финансовых операций, связанных с работой предприятия (рис. 43):
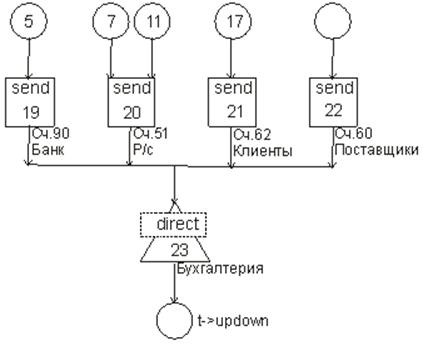
Рис. 43. Слой финансовых операций
Если время задержки платежей с расчетного счета моделируемого предприятия (обозначив эту величину через Трс) считать критическим выходным параметром, то модель можно использовать для минимизации этой величины. Основными входными параметрами моделирования будут служить цена единицы продукции, объем выпускаемой партии и сумма кредита, запрашиваемого в банке. Зафиксировав все остальные параметры (время выпуска партии, число производственных линий, интервал поступления заказа от покупателей, разброс размеров продаваемой партии, стоимость комплектующих изделий и материалов для выпуска партии, стартовый капитал на расчетном счете), можно минимизировать Трс для конкретной рыночной ситуации. Минимум Трс достигается при одном из максимумов среднего размера денежной суммы на расчетном счете. Причем вероятность рискового события - неуплаты долгов по кредитам - близка к минимуму (это можно доказать во время статистического эксперимента с моделью).
В модели первого слоя (процесс производства) имитируются следующие действия (рис. 41).
Узел 1 имитирует поступления распоряжений на изготовление партий продукции от руководства компании.
Узел 2 инициирует запрос на получение кредита, порождая для этого вспомогательный транзакт (запрос в банк).
В узле 3 запрос ожидает наступления условий, при которых кредит может быть выдан (новый предоставляется, если предыдущий кредит возвращен).
Узел 4 фиксирует наступление этих условий (переводом своего состояния в открытое) и имитирует разрешение на выдачу кредита.
Узел 5 осуществляет перечисление кредита на расчетный счет компании.
В узле 6 вспомогательный запрос уничтожается и выдается сигнал блокировки на выдачу следующего кредита (с помощью сигнальной функции hold).
Основной транзакт-распоряжение проходит через узел 2 без задержки.
В узле 7 производится оплата комплектующих, если на расчетном счете есть достаточная сумма (даже если кредит не получен). В противном случае транзакт будет ожидать поступления на расчетный счет предприятия либо кредитных денег, либо денег за проданную продукцию.
В узле 8 транзакт становится в очередь, если все производственные линии заняты.
Узел 9 (конвейерная линия) имитирует изготовление партии продукции.
В узле 10 порождается дополнительный транзакт, имитирующий заявку на возврат взятого кредита.
Эта заявка поступает в узел 11, имитирующий перечисление денег с расчетного счета предприятия в банк (если нужной суммы на счету предприятия нет, заявка ожидает).
После возврата кредита заявка уничтожается в узле 12; в банке появилась информация о том, что кредит возвращен, и компании можно выдать следующий кредит (с помощью сигнальной функции rels).
Транзакт-распоряжение проходит узел 10 без задержки и в узле 13 уничтожается. Далее считается, что партия изготовлена и поступила на склад готовой продукции.
В модели второго слоя (процесс сбыта произведенной продукции) имитируются следующие действия (рис. 42).
Узел 14 является генератором транзактов - покупателей продукции, которые обращаются на склад. Если склад располагает запрошенным количеством товара, то товар отпускается покупателю, в противном случае покупатель (транзакт) ждет.
Узел 16 имитирует отпуск товара и контроль очереди. После получения товара покупатель перечисляет деньги на расчетный счет предприятия (узел 17).
В узле 18 транзакт уничтожается (покупатель обслужен).
В модели третьего слоя (денежные операции) имитируются проводки в бухгалтерии предприятия (рис. 43).
Запросы на проводки поступают с первого слоя (рис. 41) из узлов 5, 7, 11 и из узла 17 (рис. 42). Пунктирными линиями показано движение денежных сумм по счетам 51 (Расчетный счет, узел 20), 60 (Поставщики, подрядчики, узел 22), 62 (Покупатели, заказчики, узел 21) и 90 (Банк, узел 19). Условные номера примерно соответствуют плану счетов бухгалтерского учета.
Узел 23 имитирует работу финансового директора. Обслуженные транзакты после бухгалтерских проводок попадают обратно в узлы, откуда они поступили; номера этих узлов находятся в параметре транзакта t->updown.
Ниже приводится текст программной модели:
#include <Pilgrim.h>
forward
{
float T_cust=7; /* интервал поступления заказов */
float T_work=14; /* время изготовления партии товаров */
float S_bank=10000.00; /* сумма кредита в банке */
float S_supp=10000.00; /* сумма платы поставщику */
float The_price=90.00; /* цена единица продукции */
float Mod_time=730; /* время моделирования */
int N_work=2; /* производственная мощность */
int Max=1200; /* размер производимой партии продукции*/
modbeg («Company», 23, Mod_time, (long)1234567890, none, 20, none, 18, none);
ag («Заказы»,1,none,norm,T_work,T_work/3,zero,2);
ag («Клиенты»,14,none,norm,T_cust,T_cust/3,zero,15);
assign (19,add,10000000.00); /* фонд банка */
assign (20,add,0.00); /* фонд фирмы */
assign (21,add,10000000.00); /* фонд покупателей */
network(dummy, dummy)
{
//ПРОИЗВОДСТВО ======================================
top( 2):
creat («Развилка_1», 0, 1, none, 3, 7);
place;
top( 3):
queue («ЖдемКредит», none, 4);
place;
top( 4):
key («РазрешКредита», 5);
place;
top( 5):
pay («ПереводКредита», 20, S_bank, 19, none, 19, 6); //на слой 3
place;
top( 6):
term («ЗапретВыдачи»);
hold(4);
place;
top( 7):
pay («ПлатаПоставщикам», 22, S_supp, 20, none, 20, 8); //на слой 3
place;
top( 8):
queue («ОчередьЗаказов», none, 9);
place;
top( 9):
serv («ВыполнениеЗаказов», N_work, none, norm, T_work, T_work/3, zero, 10);
place;
top(10):
creat («Развилка_2», 0, 1, none, 11, 13);
place;
top(11):
pay («ВозвратКредита», 19, S_bank, 20, none, 20, 12); //на слой 3
place;
top(12):
term («РазрешВыдачи»);
rels(4);
place;
top(13):
term («ЗаказВыполнен»);
clcode
supply(15, none, Max);
place;
///СБЫТ ================================================
top(15):
t->powr=1+rundum()*99; //объем закупаемой партии
t->summ=t->powr*The_price; //стоимость закупаемой партии
attach («СкладГотПродукции», t->powr, prty, 16);
place;
top(16):
manage («ОтпускТовара», 17);
place;
top(17):
pay («ОплатаПокупки», 20, t->summ, 21, none, 21, 18);//на слой 3
place;
top(18):
term («ТоварОплачен»);
place;
///ДЕНЕЖНЫЕ ОПЕРАЦИИ ==================================
top(19):
send («Банк_90», t->k1, t->summ, t->dpr, 23);
place;
top(20):
send («РасчСчет_51», t->k1, t->summ, t->dpr, 23);
place;
top(21):
send («Клиент_62», t->k1, t->summ, t->dpr, 23);
place;
top(22):
send («Поставщиик_60», t->k1, t->summ, t->dpr, 23);
place;
top(23):
direct («Бухгалтерия», t->updown); //на верхний слой
place;
/// ==================================================
fault (123);
}
modend («Run_061010_01.rep»,1,30,page);
return (0);
}
Пример результата запуска показан на рис. 44.
|
НАЗВАНИЕ МОДЕЛИ: |
Company |
|||||||||
|
ВРЕМЯ МОДЕЛИРОВАНИЯ: |
731 |
Лист: 1 |
||||||||
|
№ узла |
Наименование узла |
Тип узла |
Точка |
Загрузка (%=), Путь(км) |
M [t] среднее время |
C [t] квадрат коэф.вар. |
Счетчик входов и hold |
Кол. кан. |
Оcт. тр. |
Состояние узла в этот момент |
|
1 |
Заказы |
ag |
- |
- |
14 |
0.16 |
54 |
1 |
1 |
открыт |
|
2 |
Развилка_1 |
creat |
- |
- |
0 |
1.00 |
53 |
0 |
1 |
закрыт |
|
3 |
ЖдемКредит |
queue |
- |
%= 73.0 |
7 |
1.86 |
53 |
1 |
0 |
открыт |
|
4 |
РазрешКредита |
key |
- |
%= 74.4 |
12 |
1.40 |
47 |
1 |
0 |
закрыт |
|
5 |
ПереводКредита |
pay |
- |
- |
0 |
1.00 |
53 |
1 |
0 |
530000.00 P |
|
6 |
ЗапретВыдачи |
term |
- |
- |
7 |
1.86 |
53 |
0 |
0 |
открыт |
|
7 |
ПлатаПоставщика |
pay |
- |
- |
0 |
1.00 |
53 |
1 |
0 |
530000.00 P |
|
8 |
ОчередьЗаказов |
queue |
- |
%= 40.7 |
0 |
37.51 |
51 |
1 |
0 |
открыт |
|
9 |
ВыполнениеЗаказ |
serv |
- |
- |
13 |
0.10 |
51 |
2 |
1 |
открыт |
|
10 |
Развилка_2 |
creat |
- |
- |
0 |
1.00 |
50 |
0 |
0 |
открыт |
|
11 |
ВозвратКредита |
pay |
- |
- |
0 |
1.0 |
50 |
1 |
0 |
500000.00 P |
|
12 |
РазрешВыдачи |
term |
- |
- |
15 |
0.58 |
49 |
0 |
0 |
открыт |
|
13 |
ЗаказВыполнен |
term |
- |
- |
24 |
0.20 |
50 |
0 |
0 |
открыт |
|
14 |
Клиенты |
ag |
- |
- |
7 |
0.12 |
104 |
1 |
1 |
открыт |
|
15 |
СкладГотПродукц |
attach |
- |
%= 3.7 |
0 |
43.13 |
103 |
1 |
0 |
1057 S |
|
|
|
|
|
|
|
|
|
|
|
0 D |
|
16 |
ОтпускТовара |
manage |
- |
- |
0 |
1.00 |
103 |
1 |
0 |
открыт |
|
17 |
ОплатаПокупки |
pay |
- |
- |
0 |
1.00 |
103 |
1 |
0 |
476910.00 P |
|
18 |
ТоварОплачен |
term |
- |
- |
0 |
43.13 |
103 |
0 |
0 |
открыт |
|
19 |
Банк_90 |
send |
- |
- |
0 |
88.67 |
53 |
1 |
0 |
9960000.00 S |
|
|
|
|
|
|
|
|
|
|
|
0.00 D |
|
20 |
РасчСчет_51 |
send |
- |
- |
13 |
0.68 |
103 |
1 |
0 |
6910.00 S |
|
|
|
|
|
|
|
|
|
|
|
30000.00 D |
|
21 |
Клиент_62 |
send |
- |
- |
0 |
125.10 |
103 |
1 |
0 |
9523090.00 S |
|
|
|
|
|
|
|
|
|
|
|
0.00 D |
|
22 |
|
send |
- |
- |
0 |
1.0 |
|
0 |
0 |
510000.00 S |
|
|
|
|
|
|
|
|
|
|
|
0.00 D |
|
23 |
Бухгалтерия |
direct |
- |
- |
0 |
1.00 |
256 |
1 |
0 |
открыт |
Рис. 44. Отчет запуска модели бизнес-процесса
1. Для создания имитационных моделей могут применяться CASE-средства, в которых предусмотрены специальные возможности для анализа и моделирования сложных систем на основе применения методологии структурного анализа. В системе Pilgrim эта возможность реализуется с помощью конструктора Gem.
2. Структурный анализ исследуемого процесса и построение графа имитационной модели возникает задача перехода между слоями, отображающими различную степень детализации описаний. Переходы между слоями в системе Pilgrim реализуются с помощью специальных узлов модели.
3. В случаях, когда необходимо обеспечить концептуальную декомпозицию описания, используется узел parent. Этот узел не выполняет никаких действий по обработке транзакта и при генерации программного кода просто заменяется своей декомпозицией.
4. В случаях, когда необходимо осуществить декомпозицию процессов с возможностью многократного использования детального описания процесса используются узлы типа pay, rent, down. С их помощью можно создать унифицированные фрагменты модели, которые могут использоваться узлами вышележащей плоскости модели.
1. В чем состоит основное назначение конструктора Gem?
2. Какая методология положена в основу конструктора Gem?
3. Какие модели можно строить с помощью конструктора Gem?
4. Что такое декомпозиция?
5. Какие существуют разновидности декомпозиции?
6. Какую декомпозицию можно провести с помощью узла parent?
7. Какую декомпозицию можно провести с помощью узлов типа pay, rent, down?
1. Емельянов А.А., Власова Е.А., Дума Р.В. Имитационное моделирование экономических процессов / Под ред. А.А. Емельянова. – М.: Финансы и статистика, 2009. – 480 с.
· познакомиться с понятием и примерами замкнутой системы;
· получить представление о методике и приемах создания моделей замкнутой системы.
· изучить определение замкнутой системы;
· рассмотреть задачу моделирования замкнутой системы на примере корпоративной информационной системы;
· познакомиться с приемами, применяемыми для создания моделей замкнутых систем;
· освоить приемы сбора данных с помощью имитационной модели.
получите представление о:
· том, что называется замкнутой системой;
· почему важно знать способы построения моделей замкнутых систем;
· способах инициализации моделируемых процессов;
· способах отладки имитационной модели;
будете знать:
· типовые схемы «зарядки» моделей замкнутых систем;
· узлы и сигнальные функции системы Pilgrim, применяемые в схемах «зарядки» моделей замкнутых систем;
· приемы моделирования на примере модели корпоративной информационной системы.
1. Моделирование замкнутых систем.
2. Определение нестандартных выходных параметров.
3. Отладка модели.
4. Получение гистограмм.
Под моделью замкнутой системы понимается модель, в которой транзакты, будучи единожды сгенерированы, циркулируют в пределах графа модели, не погибая в терминаторах.
Такой моделью, например, может быть модель работы, группы пользователей корпоративной информационной системы с компьютерной сетью в диалоговом режиме. Транзакт в этом случае имитирует запрос пользователя. Выйдя из узла, имитирующего работу пользователя, транзакт проходит по графу модели, имитируя обработку в системе, возвращается к пользователю (узел), имитируя сформированный ответ, после чего вновь преобразуется в запрос того же пользователя.
Моделировать каждый новый запрос отдельным транзактом нельзя, так как нельзя рассчитать заранее время обработки запроса системой (это случайная величина) и, следовательно, нельзя задать частоту генератора.
В этом случае модель может быть построена следующим образом:
· Пользователи (или группы пользователей, в зависимости от сложности моделируемой системы) представляются одно- или многоканальными узлами типа serv (серверы).
· Число каналов сервера соответствует числу пользователей, время обработки транзакта сервером соответствует времени подготовки пользователями запроса.
· Конкретное состояние транзакта (запрос – ответ) фиксируется значением одного из его параметров.
· Для зарядки транзактами серверов пользователей, принадлежащих к одному классу, используется единственный генератор, порождающий всего один транзакт. Далее транзакты размножаются с помощью узлов типа creat.
Так, если требуется смоделировать работу за терминалами (клиентскими компьютерами) нескольких пользователей, причем работа каждого пользователя описывается своими временными характеристиками, то это может быть сделано следующим образом (рис. 45):
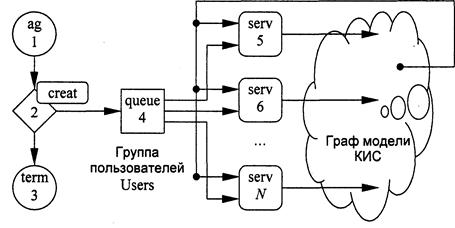
Рис. 45. Схема «зарядки» замкнутой модели
В этом графе каждый пользователь имитируется одним узлом модели типа serv. Текст программы на языке Pilgrim будет выглядеть так:
ag («Старт»,1,none, none,1.О,zero,zero,2);
top (2): creat («Размножитель», none, Users, none, 4, 3);
place;
top (3): term («Терминатор»);
cheg (1, none, none, modtime, zero, zero,3);
place;
top (4): t->ft = addr[4]->na + 5;
t->ru0 = Think_time [addr[4]->na];
t->ru1 = Query_time [addr[4]->na];
queue («Распределитель», none, t->ft) ;
place;
Значения переменных Users, modtime задают соответственно число пользователей и время моделирования, массивы Think_time и Query_time среднее время обдумывания пользователем запроса и среднее время реакции системы на запрос (значения могут устанавливаться в начале программы вместе с описаниями переменных). Конструкция реализует следующую последовательность инициализирующих действий.
Запрос, сгенерированный узлом ag (узел 1), попадает в узел creat (узел 2), который генерирует Users транзактов (по числу пользователей), не присваивая им номер семейства. Далее эти транзакты попадают в очередь (узел 4), где каждому из них присваивается свой номер семейства, равный номеру сервера, в который этот транзакт должен будет попасть после выхода из узла 2. Присваивание производится с помощью системной переменной addr[4]->na, в которой в каждый момент модельного времени хранится значение числа транзактов, прошедших через узел (в данном примере, через узел 4). Таким образом будет обеспечено автоматическое присвоению системной переменной) t->ft нужной последовательности номеров узлов-приемников.
В параметр транзакта t->ru0 заносится значение среднего времени задержки в сервере, моделирующем работу пользователя. Этот параметр используется при описании серверов пользователей (узлы с номерами из диапазона [5, Users + 4], где Users - число серверов). Кроме того, в параметр транзакта t->ru1 заносится значение среднего времени задержки запроса (обработки) в сервере, моделирующем процессор системы.
Транзакт, вышедший из узла ag и покинувший узел 2, переходит далее в терминатор (узел 3). В этом узле он инициирует выполнение сигнальной функции cheg, которая переустанавливает параметр узла ag, задающей средний интервал между двумя генерируемыми транзактами в modtime (что, по сути, означает отключение узла ag), и уничтожается.
В ряде моделей помимо выходных данных, собираемых автоматически системой Pilgrim относительно каждого из узлов графа модели, необходимо оценить также и ряд других. В частности, для систем замкнутого типа может представлять интерес время реакции моделируемой системы на пользовательский запрос. Наиболее информативным описанием случайной величины (каковой является в данном примере время реакции), как это известно из теории вероятностей, является ее распределение. Однако во многих случаях оказывается вполне достаточно ограничиться выяснением среднего значения (математического ожидания) этого параметра. Для оценивания среднего времени реакции системы на пользовательский запрос в замкнутой системе можно воспользоваться такими приемами.
1)
Значение среднего
времени реакции![]() можно рассчитать на
основании стандартного отчета с результатами моделирования системы Pilgrim. Для
этого можно воспользоваться следующим выражением:
можно рассчитать на
основании стандартного отчета с результатами моделирования системы Pilgrim. Для
этого можно воспользоваться следующим выражением:
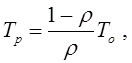
где
![]() означает среднее время обдумывания
пользователем ответа системы перед выдачей нового ей очередного запроса (вывод
этого выражение весьма несложен).
означает среднее время обдумывания
пользователем ответа системы перед выдачей нового ей очередного запроса (вывод
этого выражение весьма несложен).
2)
Значенииt ![]() можно
получить в явном виде как среднее значение нахождения узла key в
закрытом состоянии, если прибегнуть к приему, который поясним на примере
модели, рассмотренной выше.
можно
получить в явном виде как среднее значение нахождения узла key в
закрытом состоянии, если прибегнуть к приему, который поясним на примере
модели, рассмотренной выше.
Для получения нужного результата в модель нужно добавить дополнительные узлы типа key вместе с соответствующей логикой (рис. 46):
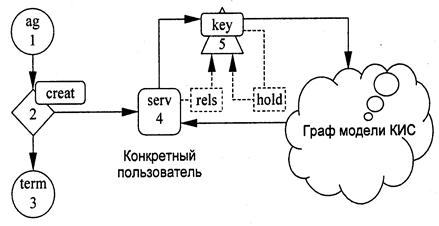
Рис. 46. Узел key как средство сбора данных
При использовании первого подхода каждому пользователю, который имитируется одним узлом типа serv, придается дополнительный узел key, который служит только для целей измерений. Транзакт (запрос к КИС) сначала попадает в узел key и запирает его с помощью сигнальной функции hold (5) (для примера выше). После обработки запроса, когда транзакт возвращается из модели КИС сервер, имитирующий пользователя, при входе в узел serv он открывает соответствующий узел key с помощью сигнальной функции rels(5) (для примера выше). В программной модели автоматически измеряется средний интервал нахождения узла key в закрытом состоянии, что и есть не что иное, как математическое ожидание, а также среднеквадратичное отклонение этой величины.
Рассмотрим следующий пример упрощенной модели КИС, граф которой включает схему зарядки, описанную ранее в настоящей теме, а граф, имитирующий обработку, состоит из одного узла типа queue, имитирующего очередь на обработку, и одного узла типа serv, имитирующего собственно обработку (Рис.):
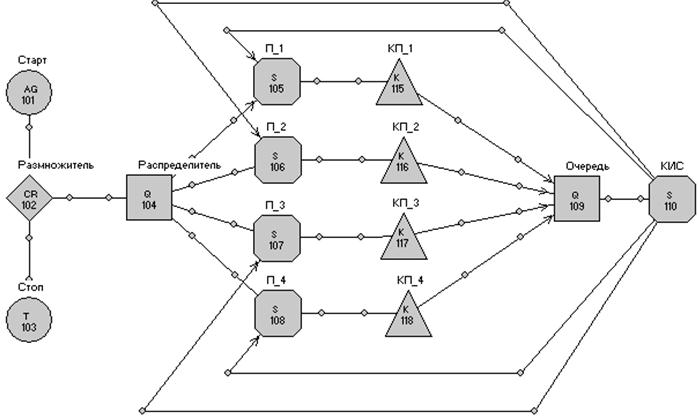
Рис. 47. Пример модели КИС
В модели присутствуют четыре пользователя, представленные узлами П_1, П_2, П_3, П_4 типа serv. Для сбора данных о времени реакции системы на запрос пользователя в модель встроены узлы КП_1, КП_2, КП_3, КП_4 типа key. Узлы 101, 102, 103 обеспечивают первоначальную зарядку транзактами узлов П_1, П_2, П_3, П_4 модели. Для некоторой совокупности параметров модели (см. значения параметров в тексте программы следующего вопроса настоящей темы) можно получить следующий результат (рис. 48):
|
НАЗВАНИЕ МОДЕЛИ: |
КИС |
|||||||||
|
ВРЕМЯ МОДЕЛИРОВАНИЯ: |
50001.00 |
Лист: 1 |
||||||||
|
№ узла |
Наименование узла |
Тип узла |
Точка |
Загрузка(%=), Путь(км) |
M [t] среднее время |
C [t] квадрат коэф.вар. |
Счетчик входов и hold |
Кол. кан. |
Оcт. тр. |
Состояние узла в этот момент |
|
|
|
|
|
|
|
|
|
|
|
|
|
101 |
Старт |
ag |
- |
- |
1.00 |
0.00 |
2 |
1 |
1 |
открыт |
|
102 |
Размножитель |
creat |
- |
- |
0.00 |
1.00 |
4 |
0 |
1 |
закрыт |
|
103 |
Стоп |
term |
- |
- |
0.00 |
1.00 |
1 |
0 |
0 |
открыт |
|
104 |
Распределитель |
queue |
- |
- |
0.00 |
1.00 |
4 |
1 |
0 |
открыт |
|
105 |
П_1 |
serv |
- |
%= 29.8 |
68.06 |
0.12 |
220 |
1 |
1 |
открыт |
|
106 |
П_2 |
serv |
- |
%= 36.9 |
93.10 |
0.14 |
198 |
1 |
0 |
открыт |
|
107 |
П_3 |
serv |
- |
%= 42.8 |
118.23 |
0.12 |
182 |
1 |
1 |
открыт |
|
108 |
П_4 |
serv |
- |
%= 48.8 |
143.59 |
0.12 |
170 |
1 |
0 |
открыт |
|
109 |
Очередь |
queue |
- |
- |
92.64 |
0.28 |
768 |
1 |
1 |
открыт |
|
110 |
КИС |
serv |
- |
%= 99.2 |
64.76 |
0.11 |
767 |
1 |
1 |
закрыт |
|
115 |
КП_1 |
key |
- |
%= 70.2 |
160.18 |
0.12 |
219 |
1 |
0 |
открыт |
|
116 |
КП_2 |
key |
- |
%= 63.4 |
160.10 |
0.12 |
198 |
1 |
0 |
закрыт |
|
117 |
КП_3 |
key |
- |
%= 56.9 |
157.26 |
0.10 |
181 |
1 |
0 |
открыт |
|
118 |
КП_4 |
key |
- |
%= 51.3 |
150.94 |
0.11 |
170 |
1 |
0 |
закрыт |
Рис. 48. Результаты запуска модели КИС
Если теперь провести сопоставление значений параметров, полученных для каждого из четырех пользователей непосредственно с помощью узлов типа key и рассчитанных по приведенной выше формуле, то результаты будут следующими (рис. 49):
|
П |
Тобд |
ρ×100% |
Треакции |
|
|
Тобд×(1-ρ)/ρ |
Key |
|||
|
1 |
68,06 |
29,8% |
160,33 |
160,18 |
|
2 |
93,10 |
36,9% |
159,20 |
160,10 |
|
3 |
118,23 |
42,8% |
158,01 |
157,26 |
|
4 |
143,59 |
48,8% |
150,65 |
150,94 |
Рис. 49. Время реакции КИС
Как видим, наблюдаемые расхождения в значениях параметров оказываются крайне незначительными.
Обязательным этапом процесса моделирования является этап обоснования модели, или подтверждения адекватности. К одному из типовых приемов, используемых для этой цели, принадлежит трассировка программной модели. Целью трассировки является построения временной диаграммы имитируемых процессов и сопоставления ее с ожидаемой. Рассмотрим возможный вариант реализации трассировки на примере упрощенной модели КИС (см. предыдущий вопрос настоящей темы),.
Ниже приводится текст программной модели, имеющей дополнительные конструкции С++, которые обеспечивают отслеживание во времени состояние транзактов модели:
/****************************************************************************/
#include <Pilgrim.h>
//Для вывода результатов трассировки ---------------------------------------------------------------------
#include <io.h> //для функции creat()
#include <fstream.h> //потоковый класс
#include <sys\stat.h> //значения параметров amode
//----------------------------------------------------------------------------------------------------------------------
forward
{
int USERS=4;
float Q_time[]={57.6,67.2,72,64.8};
float T_time[]={72, 96, 120, 144};
float modtime=50000.0;
//Выводной файл--------------------------------------------------------------------------------------------------
int fileNumb=creat («C:\\MyResults.txt», S_IWRITE); // файла для вывода
ofstream fileOut;
fileOut.attach (fileNumb);
//----------------------------------------------------------------------------------------------------------------------
modbeg («КИС», 120, modtime, (long)1234567890, none, 109, none, none, 2);
ag («Старт», 101, none, none, 1, none, none, 102);
network (dummy, dummy)
{
top (102):
creat («Размножитель», none, USERS, none, 104, 103);
place;
top (103):
term («Стоп»);
clcode
{
cheg (101,none,none,modtime,zero,zero,102);
}
place;
top (104):
t->ft=addr[104]->na + 105;
t->ru0=T_time[addr[104]->na];
t->ru1=Q_time[addr[104]->na];
queue («Распределитель», none, t->ft);
place;
top (105):
rels (115);
serv («П_1», 1, none, norm, t->ru0, t->ru0/3, none, 115);
clcode
{
fileOut << «\n» << t->ft << « Тотв=« << timer ;
}
place;
top (106):
rels (116);
serv («П_2», 1, none, norm, t->ru0, t->ru0/3, none, 116);
clcode
{
fileOut << «\n» << t->ft << « Тотв=« << timer ;
}
place;
top (107):
rels (117);
serv («П_3», 1, none, norm, t->ru0, t->ru0/3, none, 117);
clcode
{
fileOut << «\n» << t->ft << « Тотв=« << timer ;
}
place;
top (108):
rels (118);
serv («П_4», 1, none, norm, t->ru0, t->ru0/3, none, 118);
clcode
{
fileOut << «\n» << t->ft << « Тотв=« << timer ;
}
place;
top (115):
key («КП_1», 109);
hold (115);
place;
top (116):
key («КП_2», 109);
hold (116);
place;
top (117):
key («КП_3», 109);;
hold (117);
place;
top (118):
key («КП_4», 109);
hold (118);
place;
top (109):
queue («Очередь», none, 110);
clcode
{
fileOut << «\n» << t->ft << « Tвыд=« << timer ;
}
place;
top (110):
serv(«КИС», 1, none, norm, t->ru1, t->ru1/3, none, t->ft);
clcode
{
fileOut << «\n» << t->ft << « Tобс=« << timer;
}
place;
fault (123);
}
modend («КИС.rep», 1, 28, page);
return 0;
}
В программной модели присутствуют операторы, которые выводят в fileOut (описан в начальной части программы) моменты появления транзактов в основных узлах модели: Тотв (получение пользователем ответа от системы), Tвыд (выдача пользователем запроса системе), Tобс (начало обработки пользовательского запроса). Операторы записываются в блоках clcode, что гарантирует их выполнение точно в моменты вхождения транзакта в соответствующий узел.
Ниже приведен начальный фрагмент трассировки (содержимого файла C:\\MyResults.txt) без первых строк, в которой содержатся моменты первоначального занесения транзактов, сгенерированных схемой зарядки:
105 Tобс=49.9005
106 Tвыд=70.7441
107 Tвыд=93.8595
105 Тотв=121.851
106 Tобс=121.851
108 Tвыд=167.247
105 Tвыд=178.985
106 Тотв=181.122
107 Tобс=181.122
106 Tвыд=265.4
107 Тотв=274.487
108 Tобс=274.487
108 Тотв=349.432
105 Tобс=349.432
105 Тотв=370.114
106 Tобс=370.114
107 Tвыд=389.957
106 Тотв=420.103
107 Tобс=420.103
105 Tвыд=464.913
107 Тотв=476.97
105 Tобс=476.97
106 Tвыд=494.919
108 Tвыд=500.144
105 Тотв=523.164
Анализируя полученные записи можно оценить, насколько корректно воспроизводятся в имитационной модели процессы, протекающие в реальной системе.
В ряде задач результат в виде средних значений и среднеквадратичных отклонений показателей исследуемой системы бывает недостаточно информативен и требуется более подробное описание показателя, которое получается в этом случае в виде гистограмм, отображающих частоты распределения значений показателя. Собрать необходимые сведения для построения гистограммы можно непосредственным включением операторов языка С++ в текст исходного модуля pilgrim-модели. Поясним возможный прием на примере модели СМО, рассматривавшейся в предыдущих темах.
Пусть необходимо получить детальную информацию о времени нахождения заявки (транзакта) в системе. Будем собирать эти сведения в виде массива частот counts, описание которого приведем в тексте программной модели:
/* ЗАГОЛОВОЧНЫЕ ФАЙЛЫ***********************************************************/
#include <Pilgrim.h> //Pilgrim
#include <io.h> //для функции creat()
#include <fstream.h> //потоковый класс
#include <sys\stat.h> //значения параметров amode
#include <iomanip.h> //манипуляторы ввода-вывода
#include <float.h> //константы предельных значений
/*Вывод данных гистограммы ************************************************************/
void printhist (char hdr[] /* заголовок отчета */,
int fileNumb /* выводной файл */,
int dim /* размерность массивов*/,
float bounds[] /* границы значений */,
int counts[] /* частоты значений */)
{
ofstream fileOut;
int i;
float sum, mn;
fileOut.attach (fileNumb);
for ( i=0,sum=0; i<dim; sum+=counts[i++]); //сумма всех частот
for ( i=0,mn=0; i<dim; i++) //подсчет среднего
if (bounds[i]!=FLT_MIN)
if (bounds[i+1]!=FLT_MAX) mn+=counts[i]*(bounds[i]+bounds[i+1])/2/ sum;
else mn+=counts[i]* bounds[i-1] / sum;
else
if (bounds[i+1]!=FLT_MAX) mn+=counts[i]*bounds[i+1] / sum;
else mn+=counts[i] / sum;
fileOut << hdr << setprecision(4);
fileOut << «\n---------------------------------------------»
<< «\n» << setw(5)<<«MIN»<< setw(10)<<«MAX»<<setw(10)<< «N»<<setw(10)<<« % «
<< «\n---------------------------------------------»;
for ( i=0; i<dim; i++)
{
if (bounds[i]==FLT_MIN) fileOut << «\n» << setw(5) << «<<<«;
else fileOut << «\n» << setw(5) << bounds[i];
if (bounds[i+1]==FLT_MAX) fileOut <<setw(10) << «>>>«;
else fileOut <<setw(10) << bounds [i+1];
fileOut << setw(10) << counts[i] << « « << static_cast<float> (counts[i])/sum; }
fileOut << «\n---------------------------------------------»;
fileOut << «Среднее= « << mn << endl;
}
/***********************************************************************************/
forward
{
/********* ИНИЦИАЛИЗАЦИЯ СРЕДСТВ СБОРА СТАТИСТИКИ **************************/
int fileNumb=creat («C:\\MyResults.txt», S_IWRITE); // выводной файл
float bounds[]={ 0.0, 10.0, 20.0, 30.0, 40.0, 50.0, // границы интервалов
60.0, 70.0, 80.0, 90.0, 100.0, FLT_MAX }; // границы интервалов
int const dim = sizeof bounds / sizeof (float)-1; // число интервалов
int counts [dim]={ 0 }; // счетчики
ofstream fileOut; // выводной файл
fileOut.attach (fileNumb); // присоединение
int i; // индекс
//--------------------------------------------------------------------------------------------------------------------------------
modbeg («СМО», 105, 15000, (long)time(NULL), none, 102, none,104, 2);
ag («Генератор», 101, none, expo, 12.0, none, none, 102);
network (dummy, dummy)
{
top (102):
t->ru0 = timer; //Запоминание момента входа в систему
queue («Очередь «, none, 103);
place;
top (103):
serv («Сервер», 1, none, expo, 9.0, none, none, 104);
place;
top (104):
term («Терминатор»);
clcode /* Выход из системы - сбор статистики */
{
for (i=0;i<dim;i++)
if (timer-t->ru0>bounds[i] & timer-t->ru0<=bounds[i+1]) counts[i]++;
}
place;
fault(123);
}
printhist («Тпребывания «, fileNumb, dim, bounds, counts); // вывод собранной статистики
modend («pilgrim.rep», 1, 8, page);
return 0;
}
Границы интервалов изменения исследуемого показателя задаются в программе в массиве bounds, верхней границей которого являются максимально возможное значение чисел типа float (FLT_MAX).
Вывод собранных в массиве counts частот осуществляет функция printhist, в которой подсчитывается и выводится также среднее значение показателя Тср
Примером полученных статистических данных может быть (рис. 50):
Тпребывания
|
MIN |
MAX |
N |
% |
|
0 |
10 |
299 |
0.2435 |
|
10 |
20 |
240 |
0.1954 |
|
20 |
30 |
167 |
0.136 |
|
30 |
40 |
118 |
0.09609 |
|
40 |
50 |
107 |
0.08713 |
|
50 |
60 |
80 |
0.06515 |
|
60 |
70 |
81 |
0.06596 |
|
70 |
80 |
43 |
0.03502 |
|
80 |
90 |
29 |
0.02362 |
|
90 |
100 |
29 |
0.02362 |
|
100 |
>>> |
35 |
0.0285 |
Рис. 50. Пример вывода статистических данных
Используя любое доступное средство (например, построитель диаграмм Excel) числовые данные можно представить графически (рис. 51):
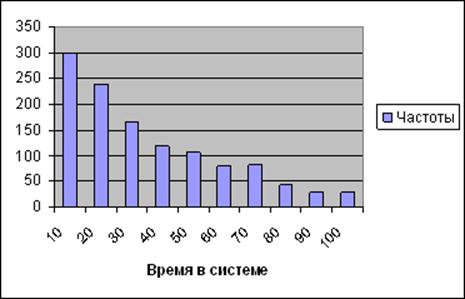
Рис. 51. Статистические данные в виде диаграммы
В необходимых случаях результат можно аппроксимировать теоретическим распределением, применяя подход, который рассматривался ранее.
Выводы:
1. Важным классом систем, для анализа и проектирования которых используется аппарат имитационного моделирования, являются замкнутые системы, в которых отсутствуют потоки между ними и внешней средой. Для создания моделей таких систем используются специальные приемы, называемые в системе Pilgrim схемами зарядки.
2. Задачами схемы зарядки являются внесение в программную модель необходимого числа транзактов, которые имитируют в случае моделирования информационной системы, пользователей системы. Для различных случаев, зависящих от характера работы и численности пользователей, разработаны специальные типовые приемы для решения этой задачи.
3. В ряде задач требуется получить результаты, не входящие в стандартный перечень, выдаваемый моделирующей системой. В таких ситуациях в моделях необходимо предусмотреть специальные средства для сбора и выдачи результатов. Эти средства реализуются применительно к специфике используемой моделирующей системы.
4. Важным этапом моделирования является этап ее отладки и обоснования адекватности модели. Для эффективной реализации этой задачи необходимо использовать различные методы и приемы. Одним из наиболее часто применяемых подходов является трассировка модели.
1. Что такое замкнутая система (модель)?
2. Почему в замкнутой модели нельзя моделировать каждый новый запрос отдельным транзактом?
3. Какие узлы используются для моделирования замкнутых систем?
4. Какие показатели могут потребоваться помимо автоматически получаемых системой Pilgrim?
5. Какими приемами можно воспользоваться для получения значения дополнительных показателей?
1. Емельянов А.А., Власова Е.А., Дума Р.В. Имитационное моделирование экономических процессов / Под ред. А.А. Емельянова. – М.: Финансы и статистика, 2009. – 480 с.
· получить представление о задачах и методиках теории планирования эксперимента и ее приложениях к имитационному моделированию.
· познакомиться с основными понятиями теории планирования эксперимента;
· рассмотреть типовые постановки задач модельных экспериментов с точки зрения теории планирования эксперимента;
· изучить подходы к решению основных задач.
получите представление о:
· области применения теории планирования эксперимента;
· задачах, решаемых теорией планирования эксперимента;
будете знать:
· как правильно формулировать задачу к исследованиям на имитационных моделях и организовывать процесс экспериментов;
· какими методами следует пользоваться для рациональной организации экспериментирования на имитационной модели;
· как отбирать существенные факторы для экспериментов на модели.
1. Основы теории планирования эксперимента.
2. Отсеивающий эксперимент.
3. Аналитическое описание функции отклика.
4. Поиск оптимальных значений.
Исследования, проводимые на имитационной модели, представляют собой частный случай научного эксперимента. Обычный подход к проведению экспериментов связан с большими временными и трудовыми затратами, поскольку сводится к последовательному варьированию отдельных совокупностей входных переменных при сохранении значений остальных неизменными, и измерению значений выходных переменных, получающихся для каждой совокупности значений входных переменных.
Эксперименты на имитационной модели являются, как правило, многофакторными и связаны с поиском рациональной структуры и оптимизацией параметров моделируемой системы, отысканием оптимальных условий ее функционирования и т.д. Степень сложности исследуемой системы и, соответственно, используемой для исследований имитационной модели в очень многих случаях не позволяет провести ее всестороннее теоретическое изучение в разумные сроки. Поэтому, несмотря на значительный объем проведенных на модели экспериментов достаточно полный анализ объекта исследования оказывается невозможным и окончательное решение получается весьма приблизительным.
Под экспериментом понимают совокупность операций, совершаемых над объектом исследования с целью получения информации о его свойствах.
Если исследователь не может самостоятельно изменять условия его проведения, а лишь регистрирует их, то это случай пассивного эксперимента.
Эксперимент, в котором исследователь по своему усмотрению может изменять условия его проведения, называется активным экспериментом. Объект, на котором возможен активный эксперимент, называется управляемым.
Опытом называется отдельная часть эксперимента.
Целью планирования эксперимента является нахождение таких условий и правил проведения опытов, при которых удается получить надежную и достоверную информацию об объекте с наименьшей затратой труда, а также представить эту информацию в компактной и удобной форме с количественной оценкой точности.
Планирование эксперимента есть процесс выбора плана эксперимента, удовлетворяющего заданным требованиям, совокупность действий направленных на разработку стратегии экспериментирования (от получения априорной информации до получения работоспособной математической модели или определения оптимальных условий). Это целенаправленное управление экспериментом, реализуемое в условиях неполного знания механизма изучаемого явления.
Результатом планирования эксперимента является план эксперимента, который представляет собой совокупность данных, определяющих число, условия и порядок проведения опытов.
Проведение исследований на основе планирования эксперимента требует выполнения некоторых требований. Основными из них являются требования управляемости (см. выше) и воспроизводимости результатов эксперимента. Воспроизводимость характеризуется разбросом значений результата определенных опытов, проводимых через неравные промежутки времени: если разброс не превышает некоторой заданной величины, то объект исследования считается удовлетворяющим требованию воспроизводимости результатов.
Хорошо составленный план эксперимента обеспечивает:
· минимизацию общего число опытов;
· одновременное варьирование всеми входными переменными;
· использование математического аппарата, формализующего многие действия экспериментатора;
· наличие четкой стратегии, позволяющей принимать обоснованные решения после каждой серии экспериментов.
Объект исследования в теории планирования эксперимента обычно представляется в виде «черного ящика» (рис. 55):

Рис. 55. Модель «черного ящика»
Входы «черного ящика» (стрелки слева), обозначенные Х1, Х2,… Хn и представляющие собой воздействия на «черный ящик», называются факторами. Кроме того, на объект воздействуют возмущающие факторы, которые являются случайными и не поддаются управлению.
Факторы, выбранные для эксперимента, должны отвечать требованиям:
· однозначности;
· независимости: факторы не должны оказывать влияния друг на друга;
· совместимости: все комбинации факторов должны быть реализуемы и не приводить к абсурду;
· управляемости: значение фактора можно задавать по усмотрению экспериментатора (предполагается активный эксперимент);
· полноты: если какой-либо существенный фактор пропущен, это приведёт к неправильному определению оптимальных условий и появлению большой ошибки опыта.
Факторы в эксперименте бывают количественными и качественными.
Количественные факторы представляются в виде значения шкалы действительных чисел. Например, число обслуживающих приборов в системе массового обслуживания.
Качественным факторам, значения которых не могут быть представлены числом, можно поставить в соответствие числовые обозначения, перейдя тем самым к количественным. Например, дисциплину обслуживания в обслуживающем приборе можно кодировать числами натурального ряда: «Первый пришел – первый обслужен»(FIFO) - 1, «Последний пришел – первый обслужен» (LIFO) - 2 и т.д.
Для каждого из факторов указывают граничные значения.
![]()
Диапазоны изменения факторов задают область определения Y. Если принять, что каждому фактору соответствует координатная ось, то полученное пространство называется факторным пространством. При n=2 область определения Y представляет собой прямоугольник, при n=3 – куб, при n >3 - гиперкуб.
Факторы могут иметь разные размерности (Мбайт, ГГц, операций/с) и различные диапазоны изменения. В теории планирования эксперимента используют кодирование факторов. Переход к кодированным (безразмерным) значениям задается преобразованием
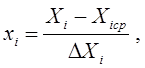
где
Хi – натуральное (абсолютное) значение фактора;
Хiср – именованное (абсолютное) значение фактора, соответствующее нулю в безразмерной шкале;
DХi – интервал варьирования фактора;
xi – кодированное значение фактора;
Если фактор является качественным, то каждому уровню этого кодированного фактора присваиваются числа в диапазоне от +1 до –1. Так при двух уровнях это +1 и –1, при трех уровнях +1, 0, -1 и т.д.
Совокупность основных уровней всех факторов представляет собой точку в пространстве параметров, называемую центральной точкой плана или центром эксперимента (Рис.).
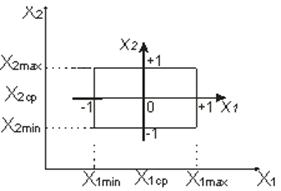
Рис. 53. Пространство параметров
С геометрической точки зрения нормализация факторов равноценна линейному преобразованию пространства факторов, при котором проводятся две операции:
1) перенос начала координат в точку, соответствующую значениям основных уровней факторов в точку с координатами Х1сp, Х2сp … , Хnсp;
2) сжатие–растяжение пространства в направлении координатных осей таким образом, что минимальное значение кодированных факторов соответствует «-1», а максимальное значение «+1».
Выходы «черного ящика называются откликом, а функция Y=F(Х1, Х2, …, Хn) – функцией отклика. Геометрическое представление функции отклика в факторном пространстве Х1, Х2, … , Хn называется поверхностью отклика (рис. 54):
|
|
|
|
Рис. 54. Поверхность отклика многофакторного эксперимента
|
Рис. 55. Поверхность отклика однофакторного эксперимента
|
Если исследуется влияние на Y лишь одного фактора Х1, то нахождение функции отклика сложностей не вызывает. Задав несколько значений фактора, в результате опытов получаем соответствующие значения Y и график Y=F(X) (рис. ):
Если факторов два, то необходимо провести опыты при разных соотношениях этих факторов. Функцию отклика в трехмерном пространстве можно графически представить в виде «контурной карты», которую можно считать видом сверху на трехмерную поверхность отклика, описывающую функцию Y (рис. 56 а), или же ее можно анализировать, проводя ряд сечений с фиксированными значениями второго (рис. 56,б) или первого факторов (рис. 56, в):
Рис. 56. Представление поверхности отклика двухфакторного эксперимента
Если уверенности в том, что опыты хорошо воспроизводятся, нет, то опыты повторяют несколько раз и получают зависимость с учетом разброса опытных данных.
По виду полученной функции отклика можно подобрать для нее математическое выражение. Подход к решению этой задачи рассмотрен в следующем вопросе темы.
Когда число факторов превышает семь, особую остроту приобретает задача выявления факторов, незначительно влияющих на показатель качества системы (функцию отклика). Планирование и проведение отсеивающего эксперимента позволяет выделить из всей совокупности факторов только наиболее существенные, подлежащие дальнейшему детальному изучению. Соответствующие планы применяют на начальных этапах исследования, когда нет конкретных сведений о влиянии тех или иных параметров. Отсеивание несущественных факторов снижает трудоемкость решения задач оптимизации или приближенного аналитического описания системы.
При проведении отсеивающих экспериментов все факторы варьируются на двух уровнях. Нижний и верхний уровень каждого фактора выбираются из технологических соображений и предшествующего опыта. Общее число опытов должно быть не меньше числа исследуемых факторов. Комбинация уровней факторов определяется матрицей планирования - таблицей, показывающей, на каком уровне устанавливается каждый конкретный фактор в каждом опыте. В этой таблице «+1» (или просто «+») означает, что фактор берется на верхнем уровне, «-1» (или «-») - на нижнем. Для качественных факторов эти понятия условны, например, «дисциплина обслуживания» на нижнем уровне может быть LIFO, на верхнем – FIFO. Важно, чтобы отличие между уровнями было как можно больше в рамках допустимых пределов работоспособности исследуемой системы. В каждом конкретном опыте уровни факторов в отсеивающем эксперименте должны быть выбраны так, чтобы матрица планирования обладала следующими свойствами (свойства ортогональности):
· сумма чисел в каждом столбце кроме первого равнялась нулю;
· сумма произведений элементов, относящихся к одному опыту, для двух любых столбцов равнялась нулю.
Примером матрицы планирования может быть следующая таблица (рис. 57):
|
Номер опыта i |
ФАКТОРЫ |
Отклик |
|||||||
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
||
|
1 |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
95 |
|
2 |
+ |
- |
+ |
- |
+ |
- |
+ |
- |
98 |
|
3 |
+ |
+ |
- |
- |
+ |
+ |
- |
- |
87 |
|
4 |
+ |
- |
- |
+ |
+ |
- |
- |
+ |
105 |
|
5 |
+ |
+ |
+ |
+ |
- |
- |
- |
- |
83 |
|
6 |
+ |
- |
+ |
- |
- |
+ |
- |
+ |
81 |
|
7 |
+ |
+ |
- |
- |
- |
- |
+ |
+ |
91 |
|
8 |
+ |
- |
- |
+ |
- |
+ |
+ |
- |
86 |
|
ΣFi+ |
|
356 |
357 |
369 |
385 |
349 |
370 |
372 |
|
|
ΣFi- |
|
370 |
369 |
357 |
341 |
377 |
356 |
354 |
|
|
ΔFi |
|
14 |
12 |
12 |
44 |
28 |
14 |
18 |
|
|
Ранг |
|
4 |
6 |
6 |
1 |
2 |
4 |
3 |
|
Рис. 57. Пример матрицы планирования отсеивающего эксперимента
Измерялась пропускная способность отделения банка в числе обслуженных клиентов в течение рабочего дня в зависимости от таких факторов как:
1 - день недели,
2 – качество помещения,
3 - район города,
4 - вид банковской операции,
5 - время (период) дня,
6 - категория клиента,
7 - квалификация кассира;
Столбец с обозначением «0» не отвечает никакому фактору, он появился вследствие правила формирования матрицы, которое поясняется ниже.
Собственно план эксперимента содержится в ячейках таблицы, заполненных символами серого цвета. Например, в опыте 5 первые три фактора берутся на верхнем уровне, а остальные четыре - на нижнем.
Чтобы
построить матрицу, обладающую свойствами ортогональности, за основу берутся так
называемые матрицы Адамара. Матрица Адамара размерности ![]() строится из матриц размерности
строится из матриц размерности ![]() по правилу:
по правилу:
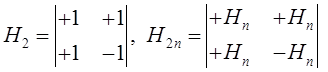
Матрица
планирования в примере рис. 57 образована матрицей ![]() ,
отсюда столбец с номером 0. С такой матрицей можно проверить влияние не более
семи факторов. Если их больше (от 8 до 15) , то следует строить матрицу
,
отсюда столбец с номером 0. С такой матрицей можно проверить влияние не более
семи факторов. Если их больше (от 8 до 15) , то следует строить матрицу![]() . Число опытов в этом случае равно 16, если
же факторов меньше 15, то просто отбрасываются последние столбцы матрицы
. Число опытов в этом случае равно 16, если
же факторов меньше 15, то просто отбрасываются последние столбцы матрицы![]() .
.
После выполнения эксперимента по данному плану анализируем его результат следующим образом.
Для каждого фактора j, j=1,…7 находится сумма значений выходного параметра по всем опытам, где j-ый фактор был на верхнем уровне (+):
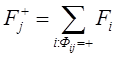
и сумму значений выходного параметра по всем опытам, где j-ый фактор был на нижнем уровне (-):
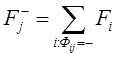
![]()
и
вносим результаты в соответствующие столбцы таблицы. Теперь ранжируем факторы
по убыванию ![]() в предположении того, что более
сильно влияющие факторы характеризуются большим значением абсолютной величины
разности. Ранг фактора вносится в нижнюю строку таблицы.
в предположении того, что более
сильно влияющие факторы характеризуются большим значением абсолютной величины
разности. Ранг фактора вносится в нижнюю строку таблицы.
Это предположение, однако, нуждается в проверке, поскольку влияние может быть вызвано как случайным сочетанием уровней других факторов, так и тем, что максимальное влияние фактора проявляется не обязательно тогда, когда он находится на верхнем или нижнем уровнях, а тогда, когда он находится на каком-то промежуточном.
Традиционные методики проведения экспериментов из-за зависимости компонентов восстанавливаемого аналитического описания не позволяют определить раздельное влияние каждого фактора на результирующий показатель, т. е. эти методики обеспечивают получение аналитических зависимостей, пригодных лишь для решения интерполяционных задач. В отличие от них теория планирования эксперимента дает возможность оценить вклад каждого параметра в значение показателя, т.е. приближенно восстановить закон функционирования объекта по экспериментальным данным. Полученное аналитическое описание объекта можно использовать для предварительного исследования вариантов построения системы или в интересах построения модели старшей системы, включающей данный объект на правах элемента. Эксперименты, направленные на раскрытие механизма исследуемого явления и определяющие аналитическую зависимость, называют интерполяционными или регрессионными.
Модель объекта представляет собой аналитическую зависимость отклика от факторов. Чаще всего эта зависимость неизвестна, известными являются факторы xi и выходные величины отклика yi. Часто встречается задача исследования одной выходной величины у как функции нескольких факторов:
yj = Fj (x1, x2, ... ,xn)
Вид этой зависимости определяется из физической сущности, а численные значения коэффициентов вычисляются в соответствии с результатами эксперимента. Поэтому модель называют также эмпирической. Модель объекта может быть построена и на основе теоретически описания происходящих процессов. В этом случае модель называется теоретической.
Одним из основных является требование простоты модели. При планировании эксперимента предполагается, что этому требованию отвечают алгебраические полиномы вида:
Y=В0 + B1Х1 + … + BnХn + В12Х1Х2 + … Вnn-1ХnХn-1 + В11Х12 + … + ВnnXn2 +….
Разложение функции в степенной ряд возможно в том случае, если сама функция является непрерывной и гладкой. На практике обычно ограничиваются числом членов степенного ряда и аппроксимируют функцию полиномом некоторой степени.
Функция отклика может быть выражена через кодированные факторы Y=f(x1,…, хn) и записана в полиномиальном виде
Y=b0 + b1x1 + b2x2 … + bnxn + b12x1x2 + … bnn-1xnxn-1 + b11x12 + … + bnnxn2 +…
Очевидно, что Bi≠bi, но
Y=F(X1,…, Xi,…, Xn) = f(x1,…, xi,…, хn)
Для полинома, записанного в кодированных факторах, степень влияния факторов или их сочетаний на функцию отклика определяется величиной их коэффициента bi.
При определении общего числа членов степенного ряда количество парных сочетаний для n факторов в полиноме, тройных сочетаний, i-ых сочетаний при n>i находится по соотношению
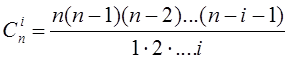
Например, для набора четырех чисел (n=4) - 1, 2, 3, 4 число тройных сочетаний составляет
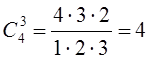 (123,
134, 124, 234)
(123,
134, 124, 234)
Если считать, что существует фактор х0 всегда равный 1, то
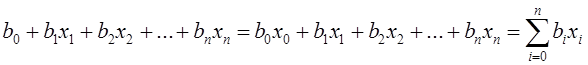
Если дополнительно все двойные, тройные и т.д. сочетания факторов, а также квадраты факторов и все соответствующие им коэффициенты для i=n+1,…m, обозначить через хi и bi, то степенной ряд можно записать в виде
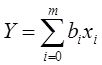
Здесь m+1 общее число рассматриваемых членов степенного ряда. Для линейного полинома с учетом всех возможных сочетаний факторов
![]()
Полный квадратичный полином будет иметь вид:
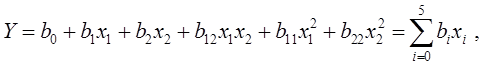
где
х0=1, х3=х1х2, х4=х12, х5=х22, b3=b12, b4=b11, b5=b22.
При использовании методов планирования эксперимента для решения задачи построения математической модели объекта необходимо найти ответы на такие вопросы:
· Какие сочетания факторов и сколько таких сочетаний необходимо взять для определения функции отклика?
· Как найти коэффициенты В0, В1, … , Bm?
· Как оценить точность представления функции отклика?
· Как использовать полученное представление для поиска оптимальных значений Y?
Математический аппарат планирования экспериментов позволяет проводить активный эксперимент и получать только необходимую информацию отдельно о каждом факторе или сочетании факторов. В частности, коэффициенты регрессии, которые являются основными характеристиками каждого фактора, определяются независимо друг от друга. Управляемость процесса получения информации заключается в том, что в процессе исследований ставятся эксперименты не по всем возможным сочетаниям факторов, а только по сочетаниям (значениям факторов в каждом эксперименте), которые обеспечат получение нужной информации. Это позволяет:
1) резко сократить количество опытов и облегчает обработку и анализ полученных результатов;
2) целенаправленно проводить исследования, четко обосновывая условия и количество экспериментов.
Если высказывается гипотеза
о линейной зависимости исследуемого процесса, то минимальное значение числа
уровней факторов в экспериментах равно двум (-1 и +1), так как прямую линию
можно построить по двум точкам. При количестве факторов равном n,
количество экспериментов N будет равно ![]() .
План, построенный таким образом, получил название полного факторного
эксперимента (ПФЭ).
.
План, построенный таким образом, получил название полного факторного
эксперимента (ПФЭ).
При многофакторном
эксперименте, особенно когда число факторов больше шести, число опытов планов
ПФЭ становится слишком большим. Если нам не требуется определение всех
коэффициентов неполного квадратичного полинома, то переходят к дробному
факторному эксперименту (ДФЭ). Они представляют собой части полного
факторного эксперимента (половину, четверть и т.д.) и называются дробными
репликами ПФЭ, в которых количество опытов N уменьшается до значения
![]() .
.
Часто возникающей на практике задачей является задача поиска значений параметров системы, обеспечивающих достижение оптимального значения показателя качества исследуемого объекта при известных ограничениях на значения параметров.
Полный перебор всех допустимых
сочетаний значений параметров системы с целью поиска оптимального варианта
нерационален с точки зрения затрат необходимых ресурсов. Например, имея всего
три фактора с пятью уровнями, потребуется провести ![]() экспериментов
для нахождения оптимальной комбинации значений.
экспериментов
для нахождения оптимальной комбинации значений.
Для нахождения оптимума может быть использован подход, называемый классическим, или методом Гаусса-Зейделя, который можно пояснить с помощью графического представления зависимости функции отклика одновременно от двух факторов в виде «контурной карты» (рис. 58Рис.):
|
|
|
|
Рис. 58. Нахождение оптимума функции отклика методом Гаусса-Зейделя |
Рис. 59. Пример некорректного результата применения метода Гаусса-Зейделя |
В методе Гаусса-Зейделя сначала находится и фиксируется наилучшее значение x1max фактора x1, и далее проводится серия экспериментов с последовательным изменением второго фактора x2 при фиксированном (найденном) значении x1.
Однако в случаях, когда кривые равного значения откликов сильно отличаются от окружностей и являются вытянутыми эллипсами, использование метода может привести и к ошибочному решению, что поясняется следующим примером (рис. 59).
Очевидно, что полученный результат (красная точка) не является оптимальным значением.
Для решения указанной задачи теория планирования эксперимента предлагает такую последовательность проведения опытов, которая позволяет применить градиентные методы поиска при априорно неизвестной функции, связывающей показатель качества с параметрами системы (функции отклика), когда варьируются одновременно все факторы, и движение на очередном шаге осуществляется в направлении наибольшего возрастания функции (рис. 60):
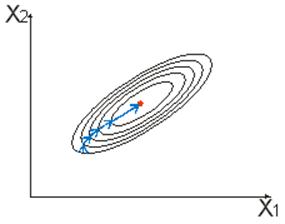
Рис. 60. Пошаговое нахождение оптимума
Метод, основанный на шаговом принципе (метод наискорейшего спуска), позволяет получать значения оптимума наиболее эффективно.
Для решения задачи поиска максимума (минимума) функции отклика используется метод факторного планирования эксперимента, который позволяет получить максимально точное решение за минимальное количество измерений.
1. Проведение экспериментов на модели направлено на решение сложных задач и может быть сопряжено с расходованием значительных ресурсов. Для эффективной организации экспериментов с моделью следует использовать методы, предлагаемые теорией планирования эксперимента и позволяющие достичь поставленной цели при минимальных требованиях к ресурсам.
2. Методы теории планирования эксперимента используют специальные понятия, стандарты и правила, предусматривающие специальную форму представления исходных данных для задачи планирования и специальную форму математического представления плана.
3. Одной из задач планирования эксперимента является задача выбора существенных факторов. Эффективным способом решения нахождения таких факторов является отсеивающий эксперимент.
4. Стратегическими целями эксперимента с моделью могут быть построение функции отклика, нахождение оптимальных значений факторов, определение существенных факторов и другие. Соответственно каждой цели моделирования должен выбираться план эксперимента, который формируется с помощью специальных методов теории планирования эксперимента.
1. Что понимают под экспериментом?
2. Какие бывают эксперименты?
3. К какому типу экспериментов относятся эксперименты на имитационной модели?
4. Почему для проведения модельных экспериментов нужно применять специальные методики?
5. Что есть планирование эксперимента?
6. При каких условиях возможно проводить исследования на основе планирования эксперимента?
7. Какие выгоды можно получить при проведении исследований на основе плана эксперимента?
8. Что называется фактором?
9. Какие бывают факторы?
10. Что такое факторное пространство?
11. В чем суть кодирования факторов?
12. Какие задачи решаются за счет кодирования факторов?
13. Что относится к типовым задачам планирования эксперимента?
14. Какие основные методы применяются для планирования эксперимента?
15. Какая из двух матриц не является матрицей планирования и почему?
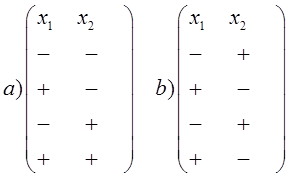
1. Емельянов А.А., Власова Е.А., Дума Р.В. Имитационное моделирование экономических процессов / Под ред. А.А. Емельянова. – М.: Финансы и статистика, 2009. – 480 с.
Узловые операторы системы Pilgrim
|
Имя/ |
Функция |
Описание |
|
ag |
Генератор транзактов с бесконечной емкостью |
Создает новые транзакты и направляет их в другие узлы модели. Параметры генератора в случае необходимости можно изменить посредством воздействия из другого узла с помощью сигнала cheg. Сигнал – специальная функция, выполненная транзактом, находящимся в одном узле, в отношении другого узла). |
|
|
||
|
queue |
Очередь с относительными приоритетами или без приоритетов |
Если приоритеты не учитываются, транзакты упорядочиваются в очереди в порядке поступления. Если приоритеты учитываются, транзакт попадает не в «хвост» очереди, а в конец своей приоритетной группы. Приоритетные группы упорядочиваются от «головы» очереди к её «хвосту» в порядке уменьшения приоритета. Если в момент прихода транзакта в очереди нет группы для приоритета пришедшего транзакта, то такая группа создается. |
|
|
||
|
serv |
Многоканальный обслуживающий узел |
Если обслуживание осуществляется без приоритетов, то транзакты попадают в первый из освободившийся каналов в порядке их поступления. Если обслуживание осуществляется по правилу абсолютных приоритетов, то в случае появления в «голове» очереди на обслуживание транзакта с ненулевым приоритетом при полностью занятых каналах и нахождении в одном из каналов транзакта с более низким приоритетом: · обслуживание неприоритетного транзакта прерывается; · неприоритетный транзакт удаляется из канала в стек временного хранения; · канал занимает более приоритетный транзакт.
После овобождения канала прерванный транзакт возвращается в канал и дообслуживается столько времени, сколько оставалось на момент прерывания. Реально возможны прерывания в прерываниях, когда на вход узнают все более приоритетные транзакты, а обслуживание происходит медленно. Глубина стека временного хранения не ограничена. |
|
|
||
|
term |
Терминатор (уничтожитель транзактов) |
Транзакт, поступающий в терминатор, уничтожается. В терминаторе фиксируется время жизни транзакта. |
|
|
||
|
creat |
Управляемый генератор (размножитель) транзактов |
Позволяет создавать новые семейства транзактов. Транзакты, создаваемые обычными генераторами принадлежат семейству с номером 0 (номер семейства - один из параметров транзакта). Если возникает необходимость создать семейство с ненулевым номером, то соответствующее требование содержится в порождающем транзакте, поступающем на вход creat. Далее за нулевое модельное время: · порождающий транзакт выходит из узла creat; · из этого же узла выходит группа новых транзактов, принадлежащих семейству с заданным номером. |
|
|
||
|
delet |
Управляемый терминатор (уничтожитель транзактов) |
Используется при необходимость уничтожить (поглотить) заданное число транзактов, принадлежащих конкретному семейству. Требование на такое действие содержится в уничтожающем транзакте, поступающем на вход узла delet. Этот транзакт ждет поступления в узел N транзактов указанного семейства и уничтожает их; время жизни при этом регистрируется. После поглощения заданного количества транзактов (или по специальному сигналу freed другого узла) уничтожающий транзакт покидает узел |
|
|
||
|
key |
Клапан (ключ) |
Если на клапан воздействовать сигналом hold из какого-либо узла, он закрывается и блокирует транзакты. Если на клапан воздействовать сигналом rels из другого узла, он открывается для прохода транзактов. Используется для синхронизации или моделирования работы с информационными ресурсами. |
|
|
||
|
dynam |
Очередь с пространственно-зависимыми приоритетами |
Транзакты, попадающие в такую очередь привязаны к точкам пространства. Очередь обслуживается специальным узлом ргос, работающим в режиме пространственных перемещений. Смысл обслуживания транзактов заключается в том, чтобы посетить все точки пространства, с которыми связаны (или из которых поступили) транзакты. При поступлении каждого нового транзакта, если он не единственный в очереди, происходит переупорядочение очереди таким образом, чтобы суммарный путь посещения точек был минимальным. В отличие от задачи коммивояжера, для решения которой в нулевой момент времени имеется вся информация о точках пространства, информация о новых точках поступает во время движения, когда некоторые точки уже посещены. Алгоритм работы узла dynam носит название алгоритма скорой помощи. |
|
|
||
|
ргос |
Управляемый процесс {непрерывный или пространственный) |
Узел работает в трех взаимоисключающих режимах: 1) моделирование управляемого непрерывного процесса (например, процесса в химическом реакторе); 2) моделирование доступа к оперативным информационным pесурсам; 3) моделирование пространственных перемещений (например, вертолета или корабля по поверхности Земли).
В первом режиме после входа транзакта в узел запускается непрерывная модель, являющаяся функцией на языке C++, имеющая параметр «время». Такой моделью могут быть математическая формула или разностное уравнение, или другое. Модель синхронизирована с другими узлами имитационной модели. Выполнением (активностью) непрерывной модели можно управлять из других узлов. Сигнал passiv вытесняет транзакт из узла ргос в стек, после чего очередные элементарные интервалы времени перестают поступать в непрерывную модель, а расчет по формуле или интегрированного разностного уравнения прекращается. Сигнал activ возвращает транзакт в узел и восстанавливает расчет по непрерывной модели. После выхода транзакта из узла выполнение непрерывной модели прекращается. Чистое время пребывания транзакта без учета вытеснения его в стек - это и время обслуживания транзакта, и время выполнения непрерывной модели. Второй режим отличается от первого тем, что непрерывные процессы в узле не моделируются, так как они не нужны для моделирования доступа к информационным ресурсам. В третьем режиме обслуживание каждого нового транзакта заключается в имитации перемещения узла ргос в новую точку пространства, координаты которой - параметры транзакта. Перемещение осуществляется с заданной скоростью. |
|
|
||
|
|
||
|
send |
Счет бухгалтерского учета («проводка») |
Транзакт, который входит в такой узел, является запросом на перечисление денег со счета на счет или на бухгалтерскую проводку. Правильность работы со счетами регулируется специальным узлом direct, который имитирует работу бухгалтерии, Транзакт, вошедший в узел send, далее может перейти только в узел direct. Если в узле send остаток денег достаточен, чтобы выполнить перевод на другой счет (в другой узел send), то узел direct выполняет перечисление и выпускает обслуженный транзакт. В противном случае в узле send возникает дефицит средств и очередь не обслуженных транзактов. |
|
|
||
|
direct |
Распорядитель финансов («главный бухгалтер») |
Управляет работой узлов типа send. Для правильной работы модели достаточно одного узла direct; он обслужит все счета без нарушения логики модели. Однако не будет ошибкой, если счет send будет обслуживаться отдельным бухгалтером. Поэтому, чтобы разделить статистику по разным участкам моделируемой бухгалтерии, можно использовать несколько узлов direct. Если при обслуживании какого-либо счета возникает дефицит ресурсов, то в этом случае возможны дисциплины обслуживания: · в хронологическом порядке поступления транзактов, · по статическим приоритетам, · по динамическим приоритетам (чем меньшую сумму нужно перечислить, тем приоритетнее транзакт). |
|
|
||
|
|
||
|
attach |
Склад перемещаемых ресурсов |
Хранилище какого-то количества однотипного ресурса (например, гаражное хозяйство, имеющее 25 грузовиков). Единицы pecypcoв в нужном количестве выделяются транзактам, поступающим в узел attach, если остаток (количество единиц, имеющихся в наличии)позволяет выполнить такое обслуживание. В противном случае возникает очередь не обслуженных транзактов и соответственно дефицит ресурса. Транзакты, получившие ресурсы, вместе с ними перемещаются по графу модели и возвращают их по мере возможности и необходимости разными способами: · все единицы вместе, · небольшими партиями, · поштучно.
На один и тот же склад транзакт может обращаться несколько раз, не возвращая ранее полученные с этого склада ресурсы. Корректность работы склада обеспечивает менеджер - узел manage. |
|
|
||
|
manage |
Менеджер (распорядитель ресурсов) |
Управляет работой узлов типа attach. Для правильной работы модели достаточно иметь один узел-менеджер; он обслужит все склады без нарушения логики модели. Однако не будет ошибкой, если склад будет обслуживаться отдельным менеджером. Поэтому, чтобы разделить статистику по разным складам перемещаемых ресурсов, можно использовать несколько узлов-менеджеров. Если при обслуживании какого-либо склада возникает дефицит ресурсов, то в этом случае возможны те же дисциплины обслуживания, которые использовались в узле direct. |
|
|
||
|
pay |
Структурный узел финансово-хозяйственных платежей |
Упрощает моделирование работы бухгалтерии. Обращения к счетам бухгалтерского учета для имитации проводок или перечислений, находящиеся в различных местах модели, усложняют граф и порождают семантические ошибки, которые очень трудно обнаруживаются. Вместо этого можно разместить граф с описанием работы бухгалтерии на одном структурном слое модели и производить обращения на этот слой в нужные входы-узлы из узла pay автоматически без графического объединения с помощью дуг. |
|
|
||
|
rent |
Структурный узел выделения ресурсов |
Применяется для упрощения графа и всей модели при работе со многими складами и с различных уровней структурной схемы точно так же, как узел pay |
|
|
||
|
down |
Произвольный структурный узел |
Необходим для упрощения сложного слоя модели путем разнесения графа по двум разным уровням (или слоям). Обеспечивает те же преимущества, что и узлы pay и rent. |
|
|
||
|
parent |
Виртуальный структурный узел |
Виртуальный узел (в тексте модели он отсутствует), используемый как средство структурного анализа при создании модели. Узел позволяет объединить множество любых узлов модели и поместить их на более низкий слой, оставив на исходном слое только значок parent. Работа с такими узлами возможна только в режиме CASE-технологии создания имитационных моделей при использовании графического конструктора. |
|
|
ID:1162918