Интернет-курс по дисциплине
«Математические методы защиты информации»

Кафедра Информационной безопасности
Шептура С.В.
Интернет-курс по дисциплине
«Математические методы защиты информации»
Содержание
Вопрос 1. История криптографии.
Вопрос 2. Основные этапы становления криптографии как
науки.
Вопрос 3. Термины и определения.
Перечень литературы и Интернет-ресурсов:
Тема 2. Характеристика информационных ресурсов,
подлежащих криптографической защите
Вопрос 1. Виды информации, подлежащие закрытию, их модели
и свойства.
Вопрос 2. Частотные характеристики открытых сообщений.
Вопрос 3. Критерии на открытый текст.
Вопрос 4. Особенности нетекстовых сообщений.
Перечень литературы и Интернет-ресурсов:
Тема 3. Криптосистема и её основные составляющие
Вопрос 1. Понятие криптосистемы.
Вопрос 2. Блочные и поточные системы.
Вопрос 3. Ключевая система шифра.
Вопрос 4. Основные требования к шифрам и криптосистемам.
Перечень литературы и Интернет-ресурсов:
Тема 4. Криптографическая стойкость шифров
Вопрос 1. Криптографическая стойкость шифров.
Вопрос 2. Ненадежность ключей и сообщений.
Вопрос 4. Безусловно, стойкие и вычислительно стойкие
шифры.
Перечень литературы и Интернет-ресурсов:
Вопрос 1. Имитация и подмена сообщения.
Вопрос 2. Характеристики имитостойкости.
Вопрос 3. Методы обеспечения имитостойкости шифров.
Вопрос 4. Совершенная имитостойкость. Коды
аутентификации.
Перечень литературы и Интернет-ресурсов:
Тема 6. Практическая реализация симметричных
криптографических алгоритмов
Вопрос 1. Криптографические стандарты. DES, AES.
Вопрос 2. Алгоритм шифрования данных, определяемый ГОСТ
28147-89.
Вопрос 3. Достоинства и недостатки симметричных систем
шифрования.
Перечень литературы и Интернет-ресурсов:
Тема 7. Асимметричные криптографические системы
(криптосистемы с открытым ключом)
Вопрос 3. Достоинства и недостатки асимметричных систем
шифрования.
Перечень литературы и Интернет-ресурсов:
Тема 8. Хэширование сообщений. Электронная цифровая
подпись
Вопрос 1. Криптографические хэш-функции. Характеристики и
алгоритмы выработки хэш-функций.
Вопрос 2. Хэширование по алгоритму ГОСТ Р 34.11-94.
Вопрос 3. Понятие электронной цифровой подписи. Стандарты
электронной цифровой подписи.
Вопрос 4. Стандарт цифровой подписи ГОСТ Р 34.10-94.
Перечень литературы и Интернет-ресурсов:
Тема 9. Протоколы обмена ключами
Вопрос 1. Понятие криптографического протокола. Основные
примеры.
Вопрос 2. Классификация криптографических протоколов.
Протоколы сертификации ключей.
Вопрос 3. Протоколы предварительного распределения
ключей.
Вопрос 4. Открытое распределение ключей Диффи-Хеллмана и
его модификации.
Перечень литературы и Интернет-ресурсов:
Курс «Математические методы защиты информации» направлен
на развитие информационных компетенций, необходимых будущим специалистам в
области информационной безопасности.
Проблема защиты информации: надежное обеспечение её
сохранности и установленного статуса использования – является одной их
важнейших проблем современности.
Среди различных методов защиты информации особое место
занимает криптография. Эпоха всепроникающих массовых коммуникаций, Интернета,
небывалой информатизации многих финансовых институтов и электронного бизнеса
привела к резкому возрастанию потребности в квалифицированных специалистах в
области криптографии.
Цели и задачи курса
Целью курса «Математические
методы защиты информации» (ММЗИ)
является ознакомление студентов с основополагающими принципами защиты
информации с помощью криптографических методов и примерами реализации этих
методов на практике.
Связь с другими дисциплинами. Для изучения дисциплины требуется знания и навыки
студентов по базовым курсам и дисциплинам специальности (предметная область), таким
как: «Информационная безопасность», «Программные и аппаратные средства
информационной безопасности» и «Безопасность и управление доступом в
информационных системах». Знания по дисциплине «Математические методы защиты
информации» могут использоваться в курсах, связанных с обоснованием, поддержкой
и принятием управленческих решений по обеспечению информационной безопасности,
а также в курсах, «Программные и аппаратные средства информационной
безопасности», «Защита и обработка конфиденциальных документов», «Прикладная
информатика» и др.
Требования к уровню освоения содержания
курса
Успешно изучив курс, студент должен:
иметь представление:
·
об основных задачах и
понятиях криптографии;
·
об этапах развития
криптографии;
·
о видах информации,
подлежащей шифрованию;
·
о классификации шифров:
·
о методах
криптографического синтеза и анализа;
·
о применениях
криптографии в решении задач аутентификации, построения систем цифровой
подписи;
·
о методах криптозащиты
компьютерных систем и сетей;
·
о государственных
стандартах в области криптографии;
знать:
·
типовые шифры замены и
перестановки;
·
частотные характеристики
языков и их использование в криптоанализе;
·
требования к шифрам и
основные характеристики шифров;
·
принципы построения
современных шифрсистем:
·
типовые поточные и
блочные шифры, системы шифрования с открытыми ключами, криптографические
протоколы;
уметь:
·
формализовать
поставленную задачу по использованию ММЗИ;
·
• выполнить постановку
задач криптоанализа и указать подходы к их решению;
·
использовать основные
математические методы, применяемые в анализе типовых криптографических алгоритмов;
·
применять полученные
знания к различным предметным областям;
обладать навыками:
·
владения
криптографической терминологией;
·
использования основных
типов шифров и криптографических алгоритмов;
·
криптоанализа простейших
шифров:
·
математического
моделирования в криптографии;
·
использования современной
научно-технической литературы в области криптографической защиты.
Основные
виды занятий. Самостоятельное
изучение. Проведение практических занятий с использованием программных средств
защиты информации. Для получения более полных прикладных (касающихся
специальности) и обзорных знаний о применении технологий защиты информации
предлагается подготовка докладов и коротких сообщений по предмету.
Цель:
Получить представление о криптографии, как об одном из
основных способов защиты информации, общих подходах к защите информации,
посредством ее математического преобразования, сформированных за всю историю
человечества.
Задачи:
1.
Изучить:
·
Формы и способы
защиты криптографической информации, принципы работы простейших аппаратных
устройств защиты информации;
·
Историю развития
методологии защиты информации с использованием математических методов.
2. Приобрести компетенции:
·
использования
терминологии криптографической защиты информации.
Содержание темы:
1.
История криптографии.
2.
Основные этапы становления криптографии как науки.
3.
Термины и определения.
История криптографии
насчитывает не одно тысячелетие. Уже в исторических документах древних
цивилизаций — Индии, Египте, Китае, Месопотамии — имеются сведения о системах и
способах составления шифрованного письма. Видимо, первые системы шифрования
появились одновременно с письменностью в четвертом тысячелетии до нашей эры.
В древнеиндийских
рукописях приводится более шестидесяти способов письма, среди которых есть и
такие, которые можно рассматривать как криптографические. Имеется описание
системы замены гласных букв согласными, и наоборот. Один из сохранившихся
шифрованных текстов Месопотамии представляет собой табличку, написанную
клинописью и содержащую рецепт изготовления глазури для гончарных изделий. В
этом тексте использовались редко употребляемые значки, игнорировались некоторые
буквы, употреблялись цифры вместо имен. В рукописях Древнего Египта шифровались
религиозные тексты и медицинские рецепты. Шифрование использовалось в Библии.
Некоторые фрагменты библейских текстов зашифрованы с помощью шифра, который
назывался атбаш.
В Древней Греции
криптография уже широко использовалась в разных областях деятельности, в особенности
в государственной сфере. Плутарх сообщает, что жрецы, например, хранили в форме
тайнописи свои прорицания. В Спарте в V — IV вв. до н. э. использовалось одно
из первых шифровальных приспособлений — Сцитала. Это был жезл
цилиндрической формы, на который наматывалась лента пергамента. Кроме жезла
могли использоваться рукоятки мечей, кинжалов копий и т.д. Вдоль оси цилиндра
на пергамент построчно записывался текст, предназначенный для передачи. После
записи текста лента сматывалась с жезла и передавалась адресату, который имел
точно такую же Сциталу. Ясно, что такой способ шифрования осуществлял перестановку
букв сообщения. Ключом шифра служит диаметр Сциталы. Известен также и метод
вскрытия такого шифра, приписываемый Аристотелю. Предлагалось заточить на конус
длинный брус и, обернув вокруг него ленту, начать сдвигать ее по конусу от
малого диаметра до самого большого. В том месте, где диаметр конуса совпадал с
диаметром Сциталы, буквы текста сочетались в слоги и слова. После этого
оставалось лишь изготовить цилиндр нужного диаметра.
Подобные шифровальные
приспособления с небольшими изменениями просуществовали до эпохи военных
походов Юлия Цезаря. Положение меняется в эпоху расцвета Рима, который
первоначально представлял собой лишь небольшую гражданскую общину, со временем
он разросся, подчинив себе сначала Италию, а затем и все Средиземноморье.
Особую роль в
сохранении тайны сыграл способ шифрования, предложенный Юлием Цезарем и
изложенный им в "Записках о галльской войне" (I в. до н.э.). Вот что
пишет о нем Гай Светоний: «...существуют и его письма к Цицерону и письма к
близким о домашних делах: в них, если нужно было сообщить что-нибудь негласно,
он пользовался тайнописью, то есть менял буквы так, чтобы из них не
складывалось ни одного слова. Чтобы разобрать и прочитать их, нужно читать
всякий раз четвертую букву вместо первой, например, D вместо А и
так далее». Таким образом, Цезарь заменял буквы в соответствии с подстановкой,
нижняя строка которой представляет собой алфавит открытого текста, сдвинутый
циклически на три буквы влево.
Со времен Цезаря до XV
в. шифровальное дело претерпело много изменений, однако нам мало известно о
методах и системах шифрования, применяемых в этот период времени. В мрачные
годы средневековья практика шифрования сохранялась в строжайшей тайне. Так, в
годы крестовых походов шифровальщики, служившие у Папы Римского, после года
работы подлежали физическому уничтожению.
В эпоху Возрождения в
итальянских городах-государствах параллельно с расцветом культуры и науки
активно развивается криптография. Нередко ученые зашифровывали научные
гипотезы, чтобы не прослыть еретиками и не подвергнуться преследованиям
инквизиции.
В последующее время в
Европе получили широкое распространение шифры, называемые номенклаторами, объединявшие
в себе простую замену и код. В простейших номенклаторах код состоял из
нескольких десятков слов или фраз с двухбуквенными кодовыми обозначениями. Со
временем списки заменяемых слов в номенклаторах увеличились до двух или трех
тысяч эквивалентов слогов и слов. В царской России XVIII в. закодированное
открытое сообщение шифровалось далее простой заменой.
Во второй половине XIX
в. появился весьма устойчивый способ усложнения числовых кодов — гаммирование.
Он заключался в перешифровании закодированного сообщения с помощью
некоторого ключевого числа, которое и называлось гаммой. Шифрование с
помощью гаммы состояло в сложении всех кодированных групп сообщения с одним и
тем же ключевым числом. Эту операцию стали называть «наложением гаммы».
XX в. «прославился»
двумя мировыми войнами. Эти войны оставили свой отпечаток на всех процессах,
происходивших в человеческом обществе. Они не могли не сказаться и на развитии
криптографии. В период первой мировой войны в качестве полевых шифров широко
использовались ручные шифры, в первую очередь шифры перестановки с различными
усложнениями.
Во второй половине XX
в., вслед за развитием элементной базы вычислительной техники, появились электронные
шифраторы, разработка которых потребовала серьезных теоретических
исследований во многих областях прикладной и фундаментальной математики, в
первую очередь алгебре, теории вероятностей и математической статистике.
Сегодня именно электронные шифраторы составляют подавляющую долю средств
шифрования. Они удовлетворяют все возрастающим требованиям по надежности и
скорости шифрования. Прогресс в развитии вычислительной техники сделал
возможными программные реализации криптографических алгоритмов, которые
все увереннее вытесняют во многих сферах традиционные аппаратные средства.
Идея Диффи и Хеллмана,
связанная с гипотетическим понятием однонаправленной (или односторонней)
функции с секретом, позволила появиться «кандидату» на такую функцию и
реально осуществить шифрсистему RSA с открытым ключом. Такая система была
предложена в
Наряду с идеей
открытого шифрования Диффи и Хеллман предложили идею открытого распределения
ключей, позволяющую избавиться от защищенного канала связи при рассылке
криптографических ключей. Их идея основывалась на сложности решения задачи дискретного
логарифмирования, то есть задачи, являющейся обратной для задачи возведения
в степень в конечном поле большого порядка.
Научные методы в
криптографии впервые появились, по-видимому, в арабских странах. Арабского
происхождения и само слово шифр. О тайнописи и ее значении говорится
даже в сказках "Тысячи и одной ночи". Первая книга, специально
посвященная описанию некоторых шифров, появилась в
В XIV в. появилась
книга о системах тайнописи, написанная сотрудником тайной канцелярии Папы
Римского Чикко Симонетти. В этой книге приводятся шифры замены, в которых
гласным буквам соответствуют несколько значковых выражений. Такие шифры позже
стали называться шифрами многозначной замены или омофонами.
Значительный шаг
вперед криптография сделала благодаря труду Леона Альберти. Известный философ,
живописец, архитектор, он в
Богатым на новые идеи
в криптографии оказался XVI в. Многоалфавитные шифры получили развитие в
вышедшей в
Еще одно важное
усовершенствование многоалфавитных систем, состоящее в идее использования в
качестве ключа текста самого сообщения или же шифрованного текста, принадлежит
Джероламо Кардано и Блезу де Виженеру. Такой шифр был назван самоключом. В
книге Виженера «Трактат о шифрах» самоключ представлен следующим образом. В
простейшем случае за основу бралась таблица Тритемия с добавленными к ней в
качестве первой строки и первого столбца алфавитами в их естественном порядке.
Позже такая таблица стала называться таблицей Виженера. Подчеркнем, что
в общем случае таблица Виженера состоит из циклически сдвигаемых алфавитов,
причем первая строка может быть произвольным смешанным алфавитом
Несколько слов о русской
криптографии. Уже с XIV в. в Новгороде существовала техника тайного письма.
Использовались в основном шифры простой замены. Благодаря торговым связям
Новгорода с Германией в России становятся известными многие западные
разработки, в том числе новые системы шифрования. Учреждение постоянной
почтовой связи России с Европой дало возможность развитию шифрованной
переписки. Благодаря привлечению Петром I для разработки проектов развития
образования и государственного устройства России знаменитого Готфрида
Вильгельма Лейбница, который известен и как криптограф, в Петербурге появилась
цифирная палата, задачами которой было развитие и использование систем
шифрования.
В истории криптографии
XVII — XVIII в. называют эрой «черных кабинетов». В этот период во
многих государствах Европы, в первую очередь во Франции, получили развитие
дешифровальные подразделения, названные "черными кабинетами". Первый
из них образован по инициативе кардинала Ришелье при дворе короля Людовика
XIII. Его возглавил первый профессиональный криптограф Франции Антуан
Россиньоль. Следует отметить, что некоторые оригинальные идеи, возникшие в криптографии
в этот период, связаны с именем самого Ришелье, который использовал, например,
для секретной переписки с королем оригинальный шифр перестановки с переменным
ключом.
Много новых идей в
криптографии принес XIX в. Изобретение в середине XIX в. телеграфа и других
технических видов связи дало новый толчок развитию криптографии. Информация
передавалась в виде токовых и бестоковых посылок, то есть представлялась в
двоичном виде. Поэтому возникла проблема "рационального"
представления информации, которая решалась с помощью кодов. Коды позволяли
передать длинное слово или целую фразу двумя-тремя знаками. Появилась
потребность в высокоскоростных способах шифрования и в корректирующих кодах,
необходимых в связи с неизбежными ошибками при передаче сообщений.
Весомый вклад в
развитие криптографии внес голландец Керкгоффс. В его книге «Военная
криптография» сформулированы 6 конкретных требований к шифрам, два из которых
относятся к стойкости шифрования, а остальные — к эксплуатационным качествам.
Одно из них («компрометация системы не должна причинять неудобств
корреспондентам») стало называться «правилом Керкгоффса». Суть этого
правила состоит в том, что стойкость (или надежность) шифра определяется
лишь секретностью ключа. Другими словами, оценка качества шифра (на основе
некоторого шифрованного текста) должна проводиться при условии, что о данном
шифре известно все, кроме использованного ключа.
Выдающиеся результаты
в применении математических методов в криптографии принадлежат Клоду Шеннону. В
В данной работе
излагается теория так называемых секретных систем, служащих фактически
математической моделью шифров. Помимо основных алгебраических (или
функциональных) свойств шифров, постулируемых в модели, множества сообщений и
ключей наделяются соответствующими априорными вероятностными свойствами, что
позволяет формализовать многие постановки задач синтеза и анализа шифров. Так,
и сегодня при разработке новых классов шифров широко используется принцип
Шеннона рассеивания и перемешивания, состоящий в использовании при
шифровании многих итераций "рассеивающих" и
"перемешивающих" преобразований.
Разработанные К.
Шенноном концепции теоретической и практической секретности (или
стойкости) позволяют количественно оценивать криптографические качества шифров
и пытаться строить в некотором смысле идеальные или совершенные
шифры. Особое место в истории криптографии XX в. занимают телефонные
шифраторы, которые были разработаны в 30-х годах и стали широко использоваться
во время второй мировой войны. В России разработка телефонного шифратора велась
под руководством В.А.Котельникова, ставшего впоследствии академиком, ученым с
мировым именем. Ему принадлежит знаменитая теорема дискретизации (или теорема
отсчетов), лежащая в основе теории цифровой обработки сигналов.
В семидесятых годах
произошло два события, серьезно повлиявших на дальнейшее развитие криптографии.
Во-первых, был принят (и опубликован!) первый стандарт шифрования данных (DES),
"легализовавший" принцип Керкгоффса в криптографии. Во-вторых, после
работы американских математиков У.Диффи и М.Хеллмана родилась "новая
криптография" — криптография с открытым ключом. Оба этих события
были рождены потребностями бурно развивающихся средств коммуникаций, в том
числе локальных и глобальных компьютерных сетей, для защиты которых
потребовались легко доступные и достаточно надежные криптографические средства.
Криптография стала широко востребоваться не только в военной, дипломатической,
государственной сферах, но также в коммерческой, банковской и других сферах.
В переводе
с греческого языка слово криптография означает тайнопись. Смысл этого термина выражает
основное предназначение криптографии –
защитить или сохранить в тайне необходимую информацию.
Криптография
дает средства для защиты информации, и поэтому она является частью деятельности
по обеспечению безопасности информации.
Традиционной
задачей криптографии является проблема обеспечения конфиденциальности
информации при передаче сообщений по контролируемому противником каналу связи.
В простейшем случае эта задача описывается взаимодействием трех субъектов
(сторон). Владелец информации, называемый обычно отправителем, осуществляет преобразование
исходной (открытой) информации (сам процесс
преобразования называется шифрованием) в форму передаваемых получателю по открытому каналу связи шифрованных сообщений с целью ее защиты от
противника.
Под противником понимается любой субъект, не
имеющий права ознакомления с содержанием передаваемой информации. В качестве
противника может выступать криптоаналитик, владеющий методами раскрытия
шифров. Законный получатель информации осуществляет расшифрование полученных сообщений.
Противник пытается овладеть защищаемой информацией (его действия обычно
называют атаками). При этом он может совершать
как пассивные, так и активные действия. Пассивные атаки связаны с прослушиванием, анализом трафика,
перехватом, записью передаваемых шифрованных сообщений, дешифрованием, т. е. попытками
"взломать" защиту с целью овладения информацией.
Подчеркнем
разницу между терминами «расшифрование» и «дешифрование». При расшифровании действующий
ключ считается известным, в то время как при дешифровании ключ неизвестен. Тем
самым расшифрование должно осуществляться столь же просто, как и зашифрование;
дешифрование представляет собой значительно более сложную задачу. Именно в этом
и состоит смысл шифрования.
При
проведении активных атак противник может прерывать процесс передачи
сообщений, создавать поддельные (сфабрикованные) или модифицировать
передаваемые шифрованные сообщения. Эти активные действия называют попытками имитации и подмены соответственно.
Под шифром обычно понимается семейство
обратимых преобразований, каждое из которых определяется некоторым параметром,
называемым ключом, а также порядком применения данного преобразования,
называемым режимом
шифрования. Ключ — это важнейший компонент шифра, отвечающий за выбор
преобразования, применяемого для зашифрования конкретного сообщения. Обычно
ключ представляет собой некоторую буквенную или числовую последовательность.
Эта последовательность как бы "настраивает" алгоритм шифрования.
Каждое
преобразование однозначно определяется ключом и описывается некоторым криптографическим
алгоритмом. Один
и тот же криптографический алгоритм может применяться для шифрования в
различных режимах. Тем самым реализуются различные способы шифрования (простая
замена, гаммирование и т. п.). Каждый режим шифрования имеет как свои преимущества,
так и недостатки. Поэтому выбор режима зависит от конкретной ситуации.
1.
А.П. Алферов, А.Ю. Зубов, А.С. Кузьмин, А.В. Черемушкин. Основы криптографии:
Учебное пособие. – М.: Гелиос АРВ, 2005. стр. 9 – 25.
2.
В.М. Фомичев. Дискретная математика и криптология Курс лекций. – М.:
ДИАЛОГ-МИФИ, 2003. стр. 100 – 110.
3.
Шаньгин В.Ф. Защита компьютерной информации. Эффективные методы и средства. –
М.: ДМК Пресс, 2008. стр. 115 – 117.
Цель:
Рассмотреть информацию, как
объект защиты. Определить основные параметры информации, способы оценки этих
параметров с точки зрения криптографической защиты.
Задачи:
1.
Изучить:
·
основные
математические модели информационных ресурсов;
·
особенности
формализации речевой информации;
·
принципы
формирования количественных характеристик сообщения.
2.
Приобрести компетенции:
·
использования
критериев оценки информационных ресурсов
·
построения
частотных характеристик сообщений.
Содержание
темы:
1.
Виды информации, подлежащие закрытию,
их модели и свойства.
2.
Частотные характеристики открытых
сообщений.
3.
Критерии на открытый текст.
4.
Особенности нетекстовых сообщений.
Математическая
модель шифра содержит вероятностные распределения Р(Х) и Р(К) на множествах открытых текстов
и ключей соответственно. Если Р(К) определяется свойствами
устройств, служащих для генерации ключей (которые могут быть случайными или
псевдослучайными), то Р(Х) определяется частотными
характеристиками самих текстов, подлежащих шифрованию. Характер таких текстов
может быть различный: это могут быть обычные литературные тексты,
формализованные данные межмашинного обмена и т. д. Так или иначе, открытые
тексты обладают многими закономерностями, некоторые из которых наследуются
шифрованными текстами. Именно это является определяющим фактором, влияющим на
надежность шифрования.
Потребность
в математических моделях открытого текста продиктована, прежде всего,
следующими соображениями. Во-первых, даже при отсутствии ограничений на
временные и материальные затраты по выявлению закономерностей, имеющих место в
открытых текстах, нельзя гарантировать того, что такие свойства указаны с
достаточной полнотой. Например, хорошо известно, что частотные свойства текстов
в значительной степени зависят от их характера. Поэтому при математических
исследованиях свойств шифров прибегают к упрощающему моделированию, в
частности, реальный открытый текст заменяется его моделью, отражающей наиболее
важные его свойства. Во-вторых, при автоматизации методов криптоанализа,
связанных с перебором ключей, требуется "научить" ЭВМ отличать
открытый текст от случайной последовательности знаков. Ясно, что
соответствующий критерий может выявить лишь адекватность последовательности
знаков некоторой модели открытого текста.
Модели открытого
текста более высоких приближений учитывают зависимость каждого знака от
большего числа предыдущих знаков. Ясно, что, чем выше степень приближения, тем
более "читаемыми" являются соответствующие модели. Проводились
эксперименты по моделированию открытых текстов с помощью ЭВМ.
Криптография
занимается защитой сообщений, содержащихся на некотором материальном носителе.
При этом сами сообщения представляют собой последовательности знаков (или слова)
некоторого алфавита. Различают естественные алфавиты,
например русский или английский, и специальные алфавиты (цифровые,
буквенно-цифровые), например двоичный алфавит, состоящий из символов 0 и 1. В
свою очередь, естественные алфавиты также могут отличаться друг от друга даже
для данного языка.
Наиболее привычны
буквенные алфавиты, например русский, английский и т. д. Приведем сведения об
алфавитах некоторых естественных европейских языков. Полный русский алфавит
состоит из 33 букв:
А Б В Г Д Е Ё Ж З И
Й К Л М Н О П Р
С Т У Ф Х Ц Ч Ш Щ Ъ
Ы Ь Э Ю Я
Вместе с тем
используются и сокращенные русские алфавиты, содержащие 32, 31 или 30 букв.
Можно отождествить буквы Е и Ё, И и Й, Ь и Ъ. Часто бывает удобно включить в
алфавит знак пробела между словами, в качестве которого можно взять, например,
символ #.
Английский алфавит
состоит из 26 букв:
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
Иногда используется
сокращенный 25-буквенный алфавит, в котором отождествлены буквы I и J.
В вычислительной
технике распространены 128-битовые и 256-битовые алфавиты, использующие
представление знаков алфавита в виде 7- или 8-значных двоичных комбинаций.
Таблица
1.
|
Символ |
Восьмеричная запись |
Двоичная запись |
|
A |
101 |
01000001 |
|
B |
102 |
01000010 |
|
C |
103 |
01000011 |
|
D |
104 |
01000100 |
|
E |
105 |
01000101 |
|
F |
106 |
01000110 |
|
1 |
061 |
00110001 |
|
2 |
062 |
00110010 |
|
3 |
063 |
00110011 |
|
4 |
064 |
00110100 |
|
& |
046 |
00100110 |
|
- |
056 |
00101110 |
|
# |
043 |
00100011 |
|
. |
054 |
00101100 |
Наиболее известен код ASCII (American
Standart Code for Information Interchange)
— американский стандартный код информационного обмена. Фрагмент этого кода
приведен в Таблице 1.
В практике передачи
сообщений по техническим каналам связи используется множество других кодов,
основанных на двоичном кодировании. Буквенный алфавит, в котором буквы расположены
в их естественном порядке, обычно называют нормальным алфавитом. В
противном случае говорят о смешанных алфавитах. В свою очередь,
смешанные алфавиты делят на систематически перемешанные алфавиты и случайные
алфавиты. К первым относят алфавиты, полученные из нормального на основе
некоторого правила, ко вторым — алфавиты, буквы которых следуют друг за другом
в хаотическом (или случайном) порядке.
Криптоанализ любого
шифра невозможен без учета особенностей текстов сообщений, подлежащих
шифрованию. Глубинные закономерности текстовых сообщений исследуются в теории
информации. Наиболее важной для криптографии характеристикой текстов является
избыточность текста, введенная К. Шенноном. Именно избыточность открытого
текста, проникающая в шифртекст, является основной слабостью шифра.
Более простыми
характеристиками текстов, используемыми в криптоанализе, являются такие
характеристики, как повторяемость букв, пар букв (биграмм) и
вообще т-ок (т-грамм), сочетаемость букв друг с другом, чередование
гласных и согласных и некоторые другие. Такие характеристики изучаются на
основе эмпирических наблюдений текстов достаточно большой длины.
Для установления
статистических закономерностей проводилась большая серия экспериментов по
оценке вероятностей появления в открытом тексте фиксированных m-грамм (для небольших значений m).
Таблица
2.
| Буква алфавита | Французский язык | Немецкий язык | Английский язык | Испанский язык | Итальянский язык |
| A | 7.68 | 5.52 | 7.96 | 12.90 | 11.12 |
| B | 0.80 | 1.56 | 1.60 | 1.03 | 1.07 |
| C | 3.32 | 2.94 | 2.84 | 4.42 | 4.11 |
| D | 3.60 | 4.91 | 4.01 | 4.67 | 3.54 |
| E | 17.76 | 19.18 | 12.86 | 14.15 | 11.63 |
| F | 1.06 | 1.96 | 2.62 | 0.70 | 1.15 |
| G | 1.10 | 3.60 | 1.99 | 1.00 | 1.73 |
| H | 0.64 | 5.02 | 5.39 | 0.91 | 0.83 |
| I | 7.23 | 8.21 | 7.77 | 7.01 | 12.04 |
| J | 0.19 | 0.16 | 0.16 | 0.24 | - |
| K | - | 1.33 | 0.41 | - | - |
| L | 5.89 | 3.48 | 3.51 | 5.52 | 5.95 |
| M | 2.72 | 1.69 | 2.43 | 2.55 | 2.65 |
| N | 7.61 | 10.20 | 7.51 | 6.20 | 7.68 |
| O | 5.34 | 2.14 | 6.62 | 8.84 | 8.92 |
| P | 3.24 | 0.54 | 1.81 | 3.26 | 2.66 |
| Q | 1.34 | 0.01 | 0.17 | 1.55 | 0.48 |
| R | 6.81 | 7.01 | 6.83 | 6.95 | 6.56 |
| S | 8.23 | 7.07 | 6.62 | 7.64 | 4.81 |
| T | 7.30 | 5.86 | 9.72 | 4.36 | 7.07 |
| U | 6.05 | 4.22 | 2.48 | 4.00 | 3.09 |
| V | 1.27 | 0.84 | 1.15 | 0.67 | 1.67 |
| W | - | 1.38 | 1.80 | - | - |
| X | 0.54 | - | 0.17 | 0.07 | - |
| Y | 0.21 | - | 1.52 | 1.05 | - |
| Z | 0.07 | 1.17 | 0.05 | 0.31 | 1.24 |
В Таблице 2 приведена
частота букв (в процентах) ряда европейских языков.
Некоторая разница
значений частот в приводимых в различных источниках таблицах объясняется тем
обстоятельством, что частоты существенно зависят не только от длины текста, но
и от его характера. Так, в технических текстах редкая буква Ф может
стать довольно частой в связи с частым использованием таких слов, как функция,
дифференциал, диффузия, коэффициент и т. п.
Еще большие отклонения
от нормы в частоте употребления отдельных букв наблюдаются в некоторых
художественных произведениях, особенно в стихах. Поэтому для надежного
определения средней частоты буквы желательно иметь набор различных текстов,
заимствованных из различных источников. Вместе с тем, как правило, подобные
отклонения незначительны, и в первом приближении ими можно пренебречь. В связи
с этим подобные таблицы, используемые в криптографии, должны составляться с
учетом характера переписки.

Рис. 1. Частоты букв английского языка (в процентах)
Наглядное
представление о частотах букв дает диаграмма встречаемости. Так, для
английского языка, в соответствии с табл. 2, такая диаграмма изображена на рис.
1.
Для русского языка
частоты (в порядке убывания) знаков алфавита, в котором отождествлены Е с Ё, Ь
с Ъ, а также имеется знак пробела (-) между словами, приведены в Таблице 3.
Таблица 3.
|
0,175 |
О 0,090 |
Е,Ё 0,072 |
А 0,062 |
|
И 0,062 |
Т 0,053 |
Н 0,053 |
С 0,045 |
|
Р 0,040 |
В 0,038 |
Л 0,035 |
К 0,028 |
|
М 0.026 |
Д 0,025 |
П 0,023 |
У 0,021 |
|
Я 0,018 |
Ы 0,016 |
З 0,016 |
Ь,Ъ 0,014 |
|
Б 0,014 |
Г 0,013 |
Ч 0,012 |
Й 0,010 |
|
Х 0,009 |
Ж 0,007 |
Ю 0,006 |
Ш 0,006 |
|
Ц 0,004 |
Щ 0,003 |
Э 0,003 |
Ф 0,002 |

Рис. 2. Диаграмма частот букв русского языка
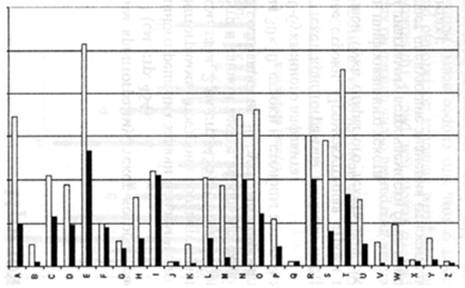
Рис. 3. Частоты
символов ASCII (буквы) (светлым — в статье по компьютерной тематике;
темным — в тексте программы на языке Паскаль)
На основании табл. 3
получаем следующую диаграмму частот.
Имеется мнемоническое
правило запоминания десяти наиболее частых букв русского алфавита. Эти буквы
составляют нелепое слово СЕНОВАЛИТР. Можно также предложить аналогичный способ
запоминания частых букв английского языка, например, с помощью слова
TETRIS-HONDA
Приведенные выше
закономерности имеют место для обычных "читаемых" открытых текстов,
используемых при общении людей. Как уже отмечалось ранее, эти закономерности
играют большую роль в криптоанализе. В частности, они используются при
построении формализованных критериев на открытый текст, позволяющих применять
методы математической статистики в задаче распознавания открытого текста в
потоке сообщений. При использовании же специальных алфавитов требуются
аналогичные исследования частотных характеристик "открытых текстов",
возникающих, например, при межмашинном обмене информацией или в системах
передачи данных. В этих случаях построение формализо-ванных критериев на
"открытый текст" — задача значительно более сложная.
В качестве примера
приведем частотные характеристики букв английского алфавита, входящих в состав
кода ASCII.
Помимо криптографии
частотные характеристики открытых сообщений существенно используются и в других
сферах. Например, клавиатура компьютера, пишущей машинки или линотипа — это
замечательное воплощение идеи ускорения набора текста, связанное с оптимизацией
расположения букв алфавита относительно друг друга в зависимости от частоты их
применения.
Заменив
реальный открытый текст его моделью, мы можем теперь построить критерий
распознавания открытого текста. При этом можно воспользоваться либо
стандартными методами различения статистических гипотез, либо наличием в
открытых текстах некоторых запретов, таких, например, как биграмма ЪЪ в русском
тексте. Проиллюстрируем первый подход при распознавании позначной модели
открытого текста.
Итак,
согласно нашей договоренности, открытый текст представляет собой реализацию
независимых испытаний случайной величины, значениями которой являются буквы
алфавита А
= {ах,...,ап}, появляющиеся в соответствии с распределением
вероятностей Р(А) = (р(ах),...,р(ап)). Требуется определить, является
ли случайная последовательность схс2...с, букв алфавита А открытым текстом или нет.
Пусть Н0
— гипотеза, состоящая в том, что данная последовательность — открытый текст, Н1
— альтернативная гипотеза. В простейшем случае последовательность c1c2...ct можно рассматривать при
гипотезе Н1 как случайную и равновероятную. Эта альтернатива
отвечает субъективному представлению о том, что при расшифровании криптограммы
с помощью ложного ключа получается «бессмысленная» последовательность знаков. В
более общем случае можно считать, что при гипотезе Н, последовательность c1c2...cs представляет собой реализацию независимых испытаний
некоторой случайной величины, значениями которой являются буквы алфавита А = {ах,...,ап}, появляющиеся в соответствии
с распределением вероятностей Q(A)i = (q(ax),..., q(an)). При таких договоренностях можно применить,
например, наиболее
мощный критерий различения двух простых гипотез, который дает лемма Неймана-Пирсона.
В силу
своего вероятностного характера такой критерий может совершать ошибки двух
родов. Критерий может принять открытый текст за случайный набор знаков. Такая
ошибка обычно называется ошибкой первого рода, ее вероятность равна а = P{Н1/Н0}.
Аналогично вводится ошибка второго рода и ее вероятность b =
P{Н0/Н1}. Эти ошибки определяют
качество работы критерия. В криптографических исследованиях естественно
минимизировать вероятность ошибки первого рода, чтобы не «пропустить» открытый
текст. Лемма Неймана-Пирсона при заданной вероятности первого рода минимизирует
также вероятность ошибки второго рода.
Критерии
на открытый текст, использующие запретные сочетания знаков, например к-граммы подряд идущих букв,
будем называть критериями запретных к -грамм. Они устроены чрезвычайно просто. Отбирается некоторое
число 5 редких к-грамм,
которые объявляются запретными. Теперь, просматривая последовательно к -грамму за к-граммой анализируемой
последовательности c1,c2…ci, мы объявляем ее случайной, как
только в ней встретится одна из запретных к - грамм, и открытым текстом в
противном случае. Такие критерии также могут совершать ошибки в принятии
решения. В простейших случаях их можно рассчитать. Несмотря на свою простоту,
критерии запретных к -грамм являются весьма эффективными.
Существуют два класса
систем связи: цифровые и аналоговые. Все наши предыдущие
исследования были связаны с цифровыми сигналами, то есть сигналами, имеющими
конечное число дискретных уровней. Аналоговые сигналы являются
непрерывными. Типичным примером такого сигнала является речевой сигнал,
передаваемый по обычному телефону. Информацию, передаваемую аналоговыми
сигналами, также необходимо защищать, в том числе и криптографическими
методами.
Имеются два различных
способа шифрования речевого сигнала. Первый состоит в перемешивании (скремблировании)
сигнала некоторым образом. Это делается путем изменения соотношений между
временем, амплитудой и частотой, не выводящих за пределы используемого
диапазона. Второй способ состоит в преобразовании сигнала в цифровую форму, к
которой применимы обычные методы дискретного шифрования.
Зашифрованное
сообщение далее передается по каналу с помощью модема. После расшифрования
полученной криптограммы вновь восстанавливается аналоговая форма сигнала.
Прежде чем перейти к деталям, необходимо остановиться на некоторых особенностях
речевых сигналов.
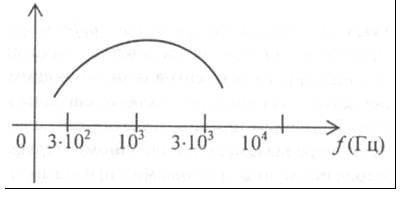
Рис. 4.
Непрерывные сигналы
характеризуются своим спектром. Спектр сигнала — это эквивалентный ему
набор синусоидальных составляющих (называемых также гармониками или частотными
составляющими). Спектр сигнала получается разложением функции, выражающей
зависимость формы сигнала от времени, в ряд Фурье. Спектр периодического
сигнала— линейчатый (дискретный), он состоит из гармоник с кратными частотами.
Спектр непериодического сигнала — непрерывный. Типичный спектр речевого сигнала
показан на рис. 4.
Частотные составляющие
в диапазонах 3-4 кГц и менее 300 Гц быстро убывают. Таким образом, очень
высокие частотные компоненты имеют существенно меньший вклад в сигнал, чем
частоты в диапазоне 500-3000 Гц. Если ограничиться частотами, не превышающими 3
кГц, и использовать высокочувствительный анализатор, то спектр, производимый
некоторыми звуками, имеет вид зубчатой кривой приблизительно следующего вида
(см. рис. 5). Мы видим несколько пиков графика, называемых формантами.
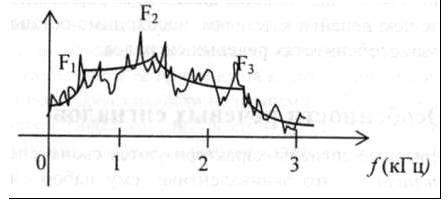
Рис. 5.
Речевой сигнал
является переносчиком смысловой информации. Эта информация при прослушивании
речевого сигнала может быть записана в виде текста сообщения. Слуховое
восприятие речевого сигнала более богато и несет как основную текстовую
информацию, так и дополнительную в виде ударений и интонаций. Элементарными
единицами слуховой информации являются элементарные звуки — фонемы, а
смысловыми единицами — звучащие слоги, слова и фразы. Для каждого языка имеется
свой набор фонем. Например, в русском и английском языках имеется около 40
фонем.
Множество фонем разбивается
на три класса. Гласные образуют одно семейство, согласные и некоторые другие
фонетические звуки (для английского языка — это, например, звуки ch, sh) образуют
два класса, называемые взрывными звуками и фрикативными звуками.
Гласные производятся движением голосовых связок под воздействием потоков
воздуха. Проходя через гортань, они превращаются в серию вибраций. Затем
воздушный поток проходит через некоторое число резонаторов, главными из которых
являются нос, рот и горло, превращаясь в воспринимаемые человеческим ухом
фонемы. Возникающие звуки зависят от формы и размеров этих резонаторов, но в
значительной степени они характеризуются низкочастотными составляющими.
Гласные звуки
производятся в течение длительного времени. Как правило, требуется около 100 мс
для достижения его пиковой амплитуды. Взрывные звуки производятся путем
«перекрытия» воздушного потока с последующим его выпусканием с взрывным
эффектом. Блокирование воздушного потока может осуществляться различными
способами — языком, нёбом или губами. Например, звук «п» произносится при
блокировании воздушного потока губами. Взрывные звуки характеризуются их
высокочастотными составляющими. До 90% их пиков амплитуды имеют длительность,
не превышающую 5 мсек. Фрикативные звуки производятся частичным перекрытием
воздушного потока, что дает звук, похожий на «белый шум». Этот звук затем
фильтруется резонаторами голосового тракта. Фрикативный звук обычно богат
пиками амплитуды длительностью 20-50 мс и сконцентрирован по частоте от 1 до 3
кГц. Пример фрикатива — звук «ссс...».
Другой важной
характеристикой человеческой речи является частота основного тона. Это —
частота вибраций голосовых связок. Среднее значение этой частоты колеблется у
разных людей, и у каждого говорящего имеется отклонение в пределах октавы выше
или ниже этой центральной частоты. Обычно у мужчины частота основного тона
колеблется около 1300 Гц, у женщины она выше.
Речевые сигналы не
только передают информацию, но и дают сведения о голосовых характеристиках
говорящего, что позволяет идентифицировать его по голосу. Можно использовать
высоту, форманты, временную диаграмму и другие характеристики речевого сигнала,
чтобы попытаться сформировать сигнал, схожий с оригиналом. Это воспроизведение
может быть в некоторой степени неестественным, и некоторые индивидуальные
характеристики говорящего будут утеряны.
1.
А.П. Алферов, А.Ю. Зубов, А.С. Кузьмин, А.В. Черемушкин. Основы криптографии:
Учебное пособие. – М.: Гелиос АРВ, 2005. стр. 25-32.
2.
В.М. Фомичев. Дискретная математика и криптология. Курс лекций. – М.:
ДИАЛОГ-МИФИ, 2003. стр. 110-115.
3.
Шаньгин В.Ф. Защита компьютерной информации. Эффективные методы и средства. –
М.: ДМК Пресс, 2008. стр. 117-122.
Цель:
Рассмотреть криптосистему, как совокупность
взаимосвязанных элементов, совместное функционирование которых обеспечивает
защиту информации. Получить представление об основных критериях классификации
шифров.
Задачи:
1.
Изучить:
·
основные элементы
криптосистемы, их функциональное назначение;
·
принципы работы
блочных и поточных шифров, достоинства и недостатки;
·
предназначение,
способы генерации и использования ключей;
·
требования к
криптосистемам и шифрам.
2.
Приобрести компетенции:
·
классификации и
выбора криптоалгоритма для практического использования;
·
оценки
эффективности криптоалгоритма, с точки зрения общепринятых требований.
Содержание темы:
1.
Понятие криптосистемы.
2.
Блочные и поточные шифры.
3.
Ключевая система шифра.
4.
Основные требования к шифрам.
В настоящие время
вместо понятия шифра используется понятие криптографической системы с секретным
ключом, которая задается следующими пятью компонентами:
1. M- пространство
открытых текстов;
3. K - пространство
ключей;
4. Ek ( k Î K ) множество преобразований зашифрования:
Ek :
M →
C (k Î K)
5. Dk (k Î K) -
множество преобразований расшифрования:
Dk :
C →
M (k Î K)
Преобразования Ek и Dk для всех (k Î K) и любого
открытого текста mÎM должны
удовлетворять условию:
Dk [Ek (m)] = m
Обобщенная схема криптосистемы шифрования
показана на рис. 6. Исходный текст передаваемого сообщения (или хранимой
информации) М зашифровывается с помощью криптографического преобразования
Еk1 с
получением в результате шифртекста
С:
С = Ek1(М),

Рис. 6. Обобщенная схема криптосистемы шифрования
где k1 — параметр функции Е, называемый ключом шифрования.
Шифртекст С, называемый
еще криптограммой, содержит исходную информацию М в
полном объеме, однако последовательность знаков в нем внешне представляется
случайной и не позволяет восстановить исходную информацию без знания ключа
шифрования k1.
Ключ шифрования является тем элементом, с помощью которого можно
варьировать результат криптографического преобразования. Данный элемент может
принадлежать конкретному пользователю или группе пользователей и являться для
них уникальным. Зашифрованная с использованием конкретного ключа информация
может быть расшифрована только его владельцем (или владельцами).
Обратное
преобразование информации выглядит следующим образом:
М’ = Dk2(С).
Функция D является
обратной к функции Е и производит расшифрование шифртекста. Она также имеет
дополнительный параметр в виде ключа k2. Ключ
расшифрования k2 должен
однозначно соответствовать ключу k1, в
этом случае полученное в результате расшифрования сообщение М будет
эквивалентно М. При отсутствии верного ключа k2 получить исходное сообщение М’ = М с
помощью функции D невозможно.
Преобразование шифрования может быть
симметричным или асимметричным относительно преобразования расшифрования.
Соответственно, различают два основных класса криптосистем:
· симметричные криптосистемы;
· асимметричные криптосистемы.
Известно несколько классификаций криптографических
алгоритмов. Одна из них подразделяет КА в зависимости от числа ключей,
применяемых в конкретном алгоритме:
· бесключевые КА - не используют
в вычислениях никаких ключей;
· одноключевые КА - работают с
одним ключевым параметром (секретным ключом);

Рис. 7. Классификация криптографических алгоритмов
·
двухключевые КА - на различных стадиях работы в них
применяются два ключевых параметра: секретный и открытый ключи.
Существуют более детальные классификации,
например, показанная на рис. 7.
Согласно основному
правилу Керкгоффса множества Ek и Dk могут быть известны не
только криптографу, но и криптоаналитику. Секретность же сообщения
обеспечивается сокрытием того факта, какое именно преобразование из известного
множества используется для зашифрования.
Современные
криптосистемы с секретным ключом подразделяются на блочные и потоковые
(поточные).
Блочное шифрование характеризуется
тем, что информация предварительно разбивается на блоки фиксированной длины
(например, 64 или 128 бит). При этом в различных криптографических алгоритмах
или даже в разных режимах работы одного и того же алгоритма блоки могут
шифроваться как независимо друг от друга, так и «со сцеплением» - когда
результат шифрования текущего блока данных зависит от значения предыдущего
блока или от результата шифрования предыдущего блока.
Блочные шифры являются той основой, на
которой реализованы практически все симметричные криптосистемы. Симметричные
криптосистемы позволяют кодировать и декодировать файлы произвольной длины.
Практически все алгоритмы используют для преобразований определенный набор
обратимых математических преобразований.
Методика создания цепочек из
зашифрованных блочными алгоритмами байтов позволяет шифровать ими пакеты
информации неограниченной длины. Отсутствие статистической корреляции между
битами выходного потока блочного шифра используется для вычисления контрольных
сумм пакетов данных и в хэшировании паролей. На сегодняшний день разработано
достаточно много стойких блочных шифров.
Криптоалгоритм считается идеально
стойким, если для прочтения зашифрованного блока данных необходим перебор всех
возможных ключей до тех пор, пока расшифрованное сообщение не окажется
осмысленным. В общем случае стойкость блочного шифра зависит только от длины
ключа и возрастает экспоненциально с ее ростом.
К. Шеннон предложил для получения стойких
блочных шифров использовать два общих принципа: рассеивание и перемешивание.
Рассеивание представляет собой распространение влияния одного знака
открытого текста на много знаков шифртекста, что позволяет скрыть
статистические свойства открытого текста.
Перемешивание предполагает использование таких шифрующих преобразований,
которые усложняют восстановление взаимосвязи статистических свойств открытого и
шифрованного текстов. Однако шифр должен не только затруднять раскрытие, но и
обеспечивать легкость зашифрования и расшифрования при известном пользователю
секретном ключе.
Распространенным способом достижения
эффектов рассеивания и перемешивания является использование составного шифра,
то есть такого шифра, который может быть
реализован в виде некоторой последовательности простых шифров, каждый из
которых вносит свой вклад в значительное суммарное рассеивание и перемешивание.
В составных шифрах в качестве простых
шифров чаще всего используются простые перестановки и подстановки. При
перестановке просто перемешивают символы открытого текста, причем конкретный
вид перемешивания определяется секретным ключом. При подстановке каждый символ
открытого текста заменяют другим символом из того же алфавита, а конкретный вид
подстановки также определяется секретным ключом. Следует заметить, что в
современном блочном шифре блоки открытого текста и шифртекста представляют
собой двоичные последовательности обычно длиной 64 или 128 бит. При длине 64
бит каждый блок может принимать 264 значений. Поэтому подстановки выполняются в очень большом
алфавите, содержащем до 264 = 1019 «символов».
При многократном чередовании простых
перестановок и подстановок, управляемых достаточно длинным секретным ключом,
можно получить стойкий шифр с хорошим рассеиванием и перемешиванием.
Все действия, производимые блочным
криптоалгоритмом над данными, основаны на том факте, что преобразуемый блок
может быть представлен в виде целого неотрицательного числа из диапазона,
соответствующего его разрядности. Например, 32-битовый блок данных можно
интерпретировать как число из диапазона 0-4294 967 295. Кроме того, блок,
разрядность которого представляет собой «степень двойки», можно трактовать как
сцепление нескольких независимых неотрицательных чисел из меньшего диапазона
(указанный выше 32-битовый блок можно также представить в виде сцепления двух
независимых 16-битовых чисел из диапазона 0-65 535 или в виде сцепления
четырех независимых 8-битовых чисел из диапазона 0-255).
Характерным признаком блочных алгоритмов
является многократное и косвенное использование материала ключа. Это
определяется в первую очередь требованием невозможности обратного декодирования
в отношении ключа при известных исходном и зашифрованном текстах. Для решения
этой задачи в приведенных выше преобразованиях чаще всего используется не само
значение ключа или его части, а некоторая, иногда необратимая функция от
материала ключа. Более того, в подобных преобразованиях один и тот же блок или
элемент ключа используется многократно. Это позволяет при выполнении условия
обратимости функции относительно величины X сделать
функцию необратимой относительно ключа К.
В шифрах потока (поточных шифрах) шифрование делается в один момент
времени над одним символом (таким, как буква или бит). Пусть имеется поток
исходного текста, поток зашифрованного текста и поток ключей. Обозначим
исходный поток Р, поток зашифрованного текста – С и поток ключей – К. Тогда
работу поточной криптосистемы можно формализовать следующим образом:
Р = Р1Р2Р3,…
С = С1С2С3,….
К = (k1,k2,k3)
C1 = Ek1(P1),
C2 = Ek2(P2),
C3 = Ek3(P3)…
Символы исходного текста принимаются
алгоритмом шифрования по одному. Символы зашифрованного текста также создаются
по одному в один и тот же момент времени. Ключевой поток может быть определен
многими способами. Это может быть только одно значение, используемое
алгоритмом. Значения могут зависеть от исходного текста или символов
зашифрованного текста. Значения могут также зависеть от предыдущих ключевых
значений.
Потоковые
криптосистемы широко используются в военных и других системах близких к ним по
назначению для шифрования данных и преобразованных в цифровую форму речевых
сигналов. Это связано, прежде всего, с относительной простотой конструирования
и реализации генераторов псевдослучайных, шифрующих последовательностей на базе
теории линейных рекуррентных последовательностей над конечными полями и других
математических дисциплин. Однако главным фактором такого применения поточных
криптосистем является отсутствие размножения ошибок. Так как при передаче
данных и речевых сообщений в стратегической связи используются каналы
недостаточно высокого качества, то любая криптосистема, которая увеличивает и
без того нередкие ошибки, неприменима. Кроме указанных приложений поточные
криптосистемы используются и при передаче данных в локальных и глобальных сетях
ЭВМ, где их непрерывное действие препятствует эффективному криптоанализу.
Главное свойство
блочных криптосистем состоит в том, что каждый бит текста шифровки является
функцией почти всех бит соответствующего блока открытого текста, и никакие два
блока открытого текста не могут быть представлены одним и тем же блоком
шифротекста. Основное их преимущество состоит в том, что даже небольшие
изменения открытого текста или ключа вызывают большие и непредсказуемые
изменения в шифротексте. Однако существенным их недостатком является
распространение (размножение) ошибки внутри блока. Результатом изменения одного
бита в принятом блоке будет неправильное расшифрование всего блока.
Возможно образование
комбинированных криптосистем поточного и блочного типа с использованием лучших
свойств каждой из них. В таких системах поточное шифрование комбинируется с
перестановками бит в блоках. Открытый текст сначала шифруется на основе шифра
замены, а затем полученный шифротекст разбивается на блоки фиксированного
размера и в каждом блоке дополнительно реализуется под управлением ключа шифр
перестановки. В результате получается шифр, не размножающий ошибки, в котором
неизвестно, какому биту открытого текста соответствует бит шифровки, что
существенно повышает стойкость криптосистемы.
Ключ — это важнейший компонент шифра, отвечающий за выбор
преобразования, применяемого для зашифрования конкретного сообщения. Обычно
ключ представляет собой некоторую буквенную или числовую последовательность.
Эта последовательность как бы "настраивает"
алгоритм шифрования. Ключ шифрования является тем элементом, с помощью которого
можно варьировать результат криптографического преобразования. Данный элемент
может принадлежать конкретному пользователю или группе пользователей и являться
для них уникальным. Зашифрованная с использованием конкретного ключа информация
может быть расшифрована только его владельцем (или владельцами).
В целом при построении шифров могут использоваться
ключи разных типов: долговременные, суточные и сеансовые (для передачи каждого
конкретного сообщения).
Более детально характеристики ключей (ключевых систем)
будут рассмотрены ниже для каждой криптосистемы.
При проведении любой
криптоатаки обычно пользуются общепринятым в криптографии правилом
Керкгоффса. В книге «Военная криптография», изданной в
1) система должна быть
нераскрываемой, если не теоретически, то практически;
2) компрометация системы не
должна причинять неудобств ее пользователям;
3) секретный ключ должен
быть легко запоминаемым без каких-либо записей;
4) криптограмма должна быть
представлена в такой форме, чтобы ее можно было передать по телеграфу;
5) аппаратура шифрования
должна быть портативной и такой, чтобы ее мог обслуживать один человек;
6) система должна быть
простой. Она не должна требовать ни запоминания длинного перечня правил, ни
большого умственного напряжения.
Второе из этих правил
и стало называться правилом Керкгоффса. Суть его состоит в том, что при
проведении криптоанализа можно считать известной систему шифрования. Стойкость
(или надежность) шифрования должна определяться лишь секретностью ключа
шифрования.
Для современных криптографических систем защиты информации сформулированы
следующие общепринятые требования:
·
зашифрованное
сообщение должно поддаваться чтению только при наличии ключа;
·
число
операций, необходимых для определения использованного ключа шифрования по
фрагменту шифрованного сообщения и соответствующего ему открытого текста,
должно быть не меньше общего числа возможных ключей;
·
число
операций, необходимых для расшифровывания информации путем перебора
всевозможных ключей должно иметь строгую нижнюю оценку и выходить за пределы
возможностей современных компьютеров (с учетом возможности использования
сетевых вычислений);
·
знание
алгоритма шифрования не должно влиять на надежность защиты;
·
незначительное
изменение ключа должно приводить к существенному изменению вида зашифрованного
сообщения даже при использовании одного и того же ключа;
·
структурные
элементы алгоритма шифрования должны быть неизменными;
·
дополнительные
биты, вводимые в сообщение в процессе шифрования, должен быть полностью и
надежно скрыты в шифрованном тексте;
·
длина
шифрованного текста должна быть равной длине исходного текста;
·
не
должно быть простых и легко устанавливаемых зависимостью между ключами,
последовательно используемыми в процессе шифрования;
·
любой
ключ из множества возможных должен обеспечивать надежную защиту информации;
·
алгоритм
должен допускать как программную, так и аппаратную реализацию, при этом
изменение длины ключа не должно вести к качественному ухудшению алгоритма
шифрования.
1.
А.П. Алферов, А.Ю. Зубов, А.С. Кузьмин, А.В. Черемушкин. Основы криптографии: Учебное
пособие. – М.: Гелиос АРВ, 2005. стр. 32-39.
2.
В.М. Фомичев. Дискретная математика и криптология Курс лекций. – М.:
ДИАЛОГ-МИФИ, 2003. стр. 115-121.
3.
Шаньгин В.Ф. Защита компьютерной информации. Эффективные методы и средства. –
М.: ДМК Пресс, 2008. стр. 122-131.
Цель:
Получить представление о
криптографической стойкости шифров – основной характеристике данного
математического преобразования, методах ее формирования, а также классификации
криптоалгоритмов по различным критериям стойкости.
Задачи:
1.
Изучить:
·
методические
подходы к оценке криптостойкости шифров;
·
проблемные вопросы,
возникающие при генерации ключей и подготовке сообщений к шифрованию;
·
практическую
реализацию идеального (совершенного) способа шифрования.
2.
Приобрести компетенции:
·
анализа
представленных на рынке криптоалгоритмов;
·
выбора
криптоалгоритмов по критерию «эффективность/стоимость».
Содержание темы:
1.
Криптографическая стойкость шифров.
2.
Ненадежность ключей и сообщений.
3.
Совершенные шифры.
4.
Безусловно, стойкие и вычислительно стойкие шифры.
Надежность или
стойкость шифров определяется объемом работы криптоаналитика, необходимой для
их вскрытия. Шифрсистема может служить объектом нападения противника,
располагающего разного уровня интеллектуальным и вычислительным потенциалом.
Нападающий может быть одиночкой хакером, имеющим персональный компьютер. Задача
криптоанализа может интересовать некую фирму, обладающую солидным персоналом и
оборудованием. Наконец, речь может идти о работе по добыванию информации мощной
государственной организацией типа АНБ США. Возможности потенциального
противника определяют требования, предъявляемые к надежности шифрования.
Исходная информация и
цели криптоаналитика могут быть разными. Несомненно, основная цель состоит в
получении конфиденциальной информации. Целью нападения может служить также
примененный секретный ключ, с помощью которого криптоаналитик может вскрывать
другие криптограммы. Шифрсистема может быть надежно защищенной от одних угроз и
быть уязвимой по отношению к другим. Попытки противника по добыванию зашифрованной
информации называют криптоатаками.
Шифры, используемые
специальными службами, всемерно охраняются. Это обусловлено необходимостью
дополнительного запаса прочности, поскольку до сих пор создание шифров с доказуемой
стойкостью является очень сложной проблемой. Обоснование надежности
шифрсистем осуществляется, как правило, теоретически и экспериментально при
моделировании криптоатак с привлечением группы высококвалифицированных
специалистов, которым предоставляются благоприятные условия для работы и необходимая
техника. На государственном уровне гарантию надежности криптографической защиты
дают уполномоченные для этой цели организации.
Рассмотрение вопросов
надежности шифрования невозможно без введения качественной и количественной
мер. В криптографии рассматривают два подхода к стойкости — теоретическую
стойкость и практическую (или вычислительную) стойкость. Но
прежде рассмотрим основной элемент шифра – ключ.
Длина ключа почти ничего не определяет в безопасности.
Внутри замка на входной двери вашего дома есть множество штырьков. Для каждого
из них существуют различные возможные положения. Когда кто-то вставляет ключ в
замочную скважину, все штырьки перемещаются в определенные позиции. Если
положение, в которое ключ ставит штырьки, как раз то, которое необходимо, чтобы
замок открылся, то он открывается. Если нет — не открывается.
У замков, наиболее часто используемых в жилых домах,
пять штырьков, каждый из которых может располагаться в одном из десяти
различных положений. Это означает, что существует 100 000 возможных ключей.
Взломщик с огромной связкой ключей может перебрать все ключи один за другим и,
в конце концов, попасть внутрь. Ему лучше набраться терпения, поскольку если
даже он тратит на один ключ 5 секунд, ему потребуется примерно 69 часов, чтобы
найти подходящий ключ.
Однако ни один взломщик не стал бы стоять перед вашей
дверью 69 часов. Он, скорее всего, откроет замок отмычкой, просверлит его,
вышибет дверь, разобьет окно или просто спрячется в кустах до тех пор, пока вы
не отправитесь на прогулку. Замок с большим количеством штырьков и положений не
обеспечит вашему дому большую безопасность, поскольку атака, которая таким
образом затрудняется — перебором еще большего количества ключей — не та атака, о
которой стоит задумываться особо. До тех пор пока количества штырьков
достаточно, чтобы сделать недопустимой такую атаку, вам не следует о ней
беспокоиться. То же самое справедливо для криптографических ключей. Если они
достаточно длинные, то лобовые атаки просто лежат за пределами человеческих
возможностей.
Но здесь следует позаботиться о двух вещах. Во-первых,
о качестве алгоритма шифрования, а во-вторых, о качестве ключа. Какой ключ
является «достаточно длинным», зависит от обеих этих вещей.
Но в первую очередь нужно разъяснить понятие энтропии.
Энтропия — мера беспорядка или, более конкретно в
контексте криптографии мера неопределенности. Чем больше неопределенность, тем
больше энтропия. Например, случайно выбранный человек из обычной популяции
является или мужчиной, или женщиной, в этом случае переменная «пол» составляет
один бит энтропии. Если случайный человек сообщает, кто из четырех «Битлз» ему
больше нравится, и все варианты равновероятны, этому соответствуют два бита
энтропии. Пол члена женской олимпийской команды по бегу — это величина, у
которой нет энтропии — они все женщины. Энтропия предпочтений одного из «Битлз»
на собрании фан-клуба Джона Леннона существенно меньше двух битов, поскольку
наиболее вероятно, что выбранный наугад человек предпочитает Джона. Чем больше
определенность переменной, тем меньше энтропия.
То же самое верно для криптографических ключей. То,
что алгоритм использует 128-битовый ключ, не означает, что у него 128 бит
энтропии для ключа. Или точнее, лучший способ сломать данную реализацию
128-битового алгоритма шифрования может состоять не в том, чтобы перебрать все
ключи. «128 бит» — это просто мера максимального количества работы, которая
потребуется, чтобы восстановить ключ; но про минимум ничего не сказано.
Затем следует позаботиться о происхождении ключа. Все
вычисления, касающиеся длины ключа, производились, исходя из предположения, что
каждый ключ имеет при создании максимальную энтропию. Другими словами, все
варианты ключа равновероятны, что генератор случайных чисел, создавший ключ,
работает идеально. Это допущение не совсем верно.
Многие ключи создаются на основе паролей и ключевых
фраз. Система, принимающая пароль из 10 ASCII-символов, предоставляет для него
80 бит, но ее энтропия будет значительно меньше 80 бит. Некоторые символы ASCII
никогда не появляются, а пароли, которые представляют собой реальные слова (или
что-то похожее на слова), гораздо вероятнее, чем произвольные строки символов.
Оценки энтропии для английского языка, меньшие 1,3 бит
на символ; у пароля энтропия меньше, чем 4 бит на символ. Это значит, что
пароль из 8 символов будет приблизительно соответствовать 32-битовому ключу, а
если вы захотите 128-битовый ключ, вам нужен пароль из 98 символов (на базе
английского алфавита). Видите ли, разумный взломщик не будет перебирать все
возможные пароли по порядку. Он сначала испробует наиболее вероятные, а затем
проверит остальные — в порядке убывания вероятности. Он проверит тривиальные
пароли (типа «пароль» или «1234»), после этого — весь английский словарь, а
затем различные заглавные буквы, цифры и т. п. Это называют словарной атакой.
Второй предмет заботы — это качество алгоритма
шифрования. Все предыдущие расчеты предполагали, что алгоритм получал ключи при
помощи вычислений и использовал их совершенным образом. Если в алгоритме есть
слабые места, доступные для атаки, это существенно снижает энтропию
ключей. Например, алгоритм А5/1,
используемый европейской сетью сотовых телефонов GSM, имеет 64-битовый ключ, но
может быть взломан за время, требующееся для взлома 30-битового ключа при
помощи атаки «в лоб». Это значит, что хотя у алгоритма имеется ключ с
64-битовой энтропией, он задействует для ключа только 30 бит энтропии.
Вы можете с тем же успехом использовать хороший
алгоритм с 30-битовым ключом. По этой причине проходит довольно много времени,
прежде чем шифровальщики начинают доверять новому алгоритму. Когда кто-то
предлагает новый алгоритм, у него есть определенная длина ключа. Но
обеспечивает ли алгоритм реально ту энтропию, которая заявлена? Может потребоваться
несколько лет анализа, прежде чем мы поверим, что он это делает. И даже тогда
мы можем легко ошибиться: возможно, кто-то придумает новые математические
подходы, которые понизят энтропию алгоритма и сломают его. Поэтому рекламу
программ, в которых обещаются тысячебитовые ключи, трудно воспринимать серьезно
— ее создатели не имеют понятия, как работают ключи и энтропия.
Рассмотрим идеальный способ шифрования. Он называется одноразовым
блокнотом и был изобретен в 1917 году Мэйджором Джозефом Моборном ( Major Joseph Mauborgne) и Гилбертом Вернамом (Gilbert Vernam)
из AT&T. В классическом понимании одноразовый блокнот является большой
неповторяющейся последовательностью символов ключа, распределенных случайным
образом, написанных на кусочках бумаги и приклеенных к листу блокнота.
Первоначально это была одноразовая лента для
телетайпов. Отправитель использовал каждый символ ключа блокнота для шифрования
только одного символа открытого текста. Шифрование представляет собой сложение
по модулю 26 символа открытого текста и символа ключа из одноразового блокнота.
Каждый символ ключа используется только единожды и для единственного
сообщения. Отправитель шифрует сообщения и уничтожает использованные страницы
блокнота или использованную часть ленты. Получатель, в свою очередь, используя
точно такой же блокнот, дешифрирует каждый символ шифротекста. Расшифровав
сообщение, получатель уничтожает соответствующие страницы блокнота или часть
ленты. Новое сообщение - новые символы ключа. Например, если сообщением
является:
ONЕTIMHPAD а
ключевая последовательность в блокноте:
TBFRGKARFM то шифротекст будет выглядеть как:
IPKLPSFHGQ так как
Q + T mod 26 = I
N
+ В mod
26 = Р
Е + F mod 26 = К
и т. д.
В предположении, что злоумышленник не сможет получить
доступ к одноразовому блокноту, использованному для шифрования сообщения, эта
схема совершенно безопасна. Данное шифрованное сообщение на вид соответствует
любому открытому сообщению того же размера.
Так как все ключевые последовательности совершенно одинаковы (помните,
символы ключа генерируются случайным образом), у противника отсутствует
информация, позволяющая подвергнуть шифротекст криптоанализу. Кусочек
шифротекста может быть похож на:
POYYAEAAZX, что
дешифрируется как:
SALMONEGGS или на:
ВXНСIВMTVI,
что
дешифрируется как:
GREENFLUID
Повторю еще раз: так как все открытые тексты равновероятны, у
криптоаналитика нет возможности определить, какой из открытых текстов является
правильным. Случайная ключевая последовательность, сложенная с неслучайным
открытым текстом, дает совершенно случайный шифротекст, и никакие
вычислительные мощности не смогут это изменить.
Необходимо напомнить, что символы ключа должны генерироваться случайным
образом. Любые попытки вскрыть такую схему сталкиваются со способом, которым
создается последовательность символов ключа. Использование генераторов
псевдослучайных чисел не считается, у них всегда неслучайные свойства. Если вы
используете действительно случайный источник - это намного труднее, чем кажется
на первый взгляд,- это совершенно безопасно. Другой важный момент ключевую
последовательность никогда нельзя использовать второй раз. Даже если вы
используете блокнот размером в несколько гигабайт, то если криптоаналитик
получит несколько текстов с перекрывающимися ключами, он сможет восстановить
открытый текст. Он сдвинет каждую пару шифротекстов относительно друг друга и
подсчитает число совпадений в каждой позиции. Если шифротексты смещены
правильно, соотношение совпадений резко возрастет - точное значение зависит от
языка открытого текста. С этой точки зрения криптоанализ не представляет труда.
Не используйте ключевую последовательность повторно.
Идея одноразового блокнота легко расширяется на двоичные данные. Вместо
одноразового блокнота, состоящего из букв, используется одноразовый блокнот из
битов. Вместо сложения открытого текста с ключом одноразового блокнота
используйте XOR. Для дешифрирования примените
XOR к шифротексту с тем же одноразовым блокнотом. Все
остальное не меняется, и безопасность остается такой же совершенной.
Все это хорошо, но существует несколько проблем. Так как ключевые биты
должны быть случайными и не могут использоваться снова, длина ключевой
последовательности должна равняться длине сообщения. Одноразовый блокнот удобен
для нескольких небольших сообщений, но его нельзя использовать для работы по
каналу связи с пропускной способностью 1,544 Мбит/с. Вы можете хранить 650
Мбайт случайных данных на CD-ROM,
но и тут есть проблемы. Во-первых, вам нужно только две копии случайных битов,
но CD-ROM экономичны только при больших
тиражах. И во-вторых, вам нужно уничтожать использованные биты. Для CD-ROM
нет другой возможности удалить информацию кроме как физически разрушить весь
диск. Гораздо больше подходит цифровая лента.
Даже если проблемы распределения и хранения ключей решены, вам придется
точно синхронизировать работу отправителя и получателя. Если получатель
пропустит бит (или несколько бит пропадут при передаче), сообщение потеряет
всякий смысл. С другой стороны, если несколько бит изменятся при передаче (и ни
один бит не будет удален или добавлен - что гораздо больше похоже на влияние
случайного шума), то лишь эти биты будут расшифрованы неправильно. Но
одноразовый блокнот не обеспечивает проверку подлинности.
При рассмотрении
вопроса о теоретической стойкости шифров отвлекаются от реальных временных и
стоимостных затрат по вскрытию шифра (что определяет подход к практической
стойкости). Во главу угла ставится принципиальная возможность получения
некоторой информации об открытом тексте или использованном ключе. Впервые такой
подход исследовал К. Шеннон. Он рассматривал уже знакомую нам модель шифра и
единственную криптоатаку на основе шифртекста. Проследим за его рассуждениями.
Как мы указывали, конечной целью работы криптоаналитика является текст
сообщения или ключ шифрования. Однако весьма полезной может быть даже некоторая
вероятностная информация об открытом тексте. Например, уже предположение о том,
что открытый текст написан по-английски, предоставляет криптоаналитику
определенную априорную информацию об этом сообщении даже до того, как он увидит
шифртекст. Так, например, он заранее знает, что слово "hello"
является более вероятным началом сообщения, чем, скажем, набор букв
"abcde". Поэтому первая цель криптоанализа состоит в том, чтобы
увеличить количество этой априорной информации, относящейся к каждому
возможному открытому тексту таким образом, чтобы истинный открытый текст
сделать более вероятным после получения шифртекста, хотя, конечно, и не
обязательно точным. Пусть, например, криптоаналитик перехватил текст
"abccd" и знает (или предполагает), что он был зашифрован при помощи
шифра простой замены. Этот шифртекст говорит ему о том, что открытый текст
состоит из пяти букв, третья и четвертая из которых являются одинаковыми, а
остальные отличными от этой буквы и разными. Хотя он не может быть уверенным,
что этим словом является "hello" (это может быть еще
"lessy" или что-то подобное), тем не менее апостериорные
вероятности таких открытых текстов возрастают относительно их априорных
вероятностей. Криптоаналитик, кроме того, полностью уверен (в предположении,
что использовалась именно простая замена) в том, что этот открытый текст не
может быть ни словом "after", ни словом "catch", и, таким
образом, апостериорная вероятность обоих этих открытых априорных вероятностей.
Шеннон назвал шифр совершенным,
если для любого открытого текста знания, которые могут быть получены из
соответствующего ему шифртекста, не раскрывают никакой информации об открытом
тексте, за исключением, возможно, его длины. Другими словами, для совершенных
шифров апостериорные вероятности открытых текстов (вычисленные после получения
криптограммы) совпадают с их априорными вероятностями.
Рассматривая практическую стойкость шифров
предполагается, что для рассматриваемого шифра, обычно будет существовать
единственное решение (х или к) криптограммы. Задача дешифрования и
состоит в нахождении этого единственного решения, имеющего высокую вероятность
(р(х/у) или р(к/у)). До того как объем перехвата достигнет
расстояния единственности, задача состоит в нахождении всех решений, имеющих
большую вероятность (по сравнению с остальными решениями), и, конечно, в
определении вероятностей этих решений.
Несмотря на то, что
эти решения можно в принципе найти, поочередно перебирая, например, все ключи
при расшифровании, для различных шифров нужно будет затратить для этого весьма
различающиеся объемы работы. Средний объем работы W(N), необходимый для
определения ключа по криптограмме, состоящей из N букв, измеренный в
удобных элементарных операциях, К.Шеннон предложил назвать рабочей
характеристикой шифра. Это среднее значение берется по всем сообщениям и
всем ключам с соответствующими им вероятностями. Функция W(N) характеризует
средние затраты (временные и материальные), необходимые для практического
дешифрования криптограммы. Подобную характеристику можно рассматривать не
только для одной конкретной криптоатаки, но и для других постановок задач
криптоанализа простой замены, сопоставив ее с неопределенностью шифра по
открытому тексту (как функцией длины сообщения).
Наибольший интерес представляет предельное значение
W(N) при N →∞ (то есть W(∞)), которое можно рассматривать как
среднюю работу по дешифрованию при неограниченном объеме шифртекста.
Практическое вычисление W(∞) представляет собой весьма сложную задачу. В
связи с этим практическую стойкость шифра обычно оценивают с помощью величины
W(∞), которую можно назвать достигнутой оценкой рабочей характеристики.
Она определяется средней трудоемкостью наилучшего из известных методов вскрытия
данного шифра. Если значение W(∞) вычисляет криптоаналитик, которому
известны все имеющиеся в настоящее время методы анализа шифров, то полученная
оценка практической стойкости шифра заслуживает доверия, особенно если
вычисления сделаны с достаточным «запасом». Имеется в виду правильный выбор
нижнего порога сложности выделяющий практически стойкие шифры.
Большое значение имеет математическая модель
вычислений, используемая при оценке практической стойкости шифра. По сути, речь
идет о модели гипотетической ЭВМ, которой располагает потенциальный противник и
которая способна реализовать крупный фрагмент алгоритма вскрытия как одну
элементарную операцию. Например, опробование одного ключа и проверку результата
расшифрования по критерию открытого текста
1.
А.П. Алферов, А.Ю. Зубов, А.С. Кузьмин, А.В. Черемушкин. Основы криптографии:
Учебное пособие. – М.: Гелиос АРВ, 2005. стр. 39-45.
2.
В.М. Фомичев. Дискретная математика и криптология Курс лекций. – М.:
ДИАЛОГ-МИФИ, 2003. стр. 121-128.
3.
Шаньгин В.Ф. Защита компьютерной информации. Эффективные методы и средства. –
М.: ДМК Пресс, 2008. стр. 131-140.
Цель:
Рассмотреть имитостойкость,
как характеристику шифра наиболее полно отражающую способность криптосистемы
противостоять наиболее опасным атакам со стороны неавторизованных лиц, а также
методы обеспечения имитостойкости.
Задачи:
1.
Изучить:
·
формы и способы
действий неавторизованных лиц направленных на нарушение целостности и
достоверности информации;
·
параметры,
характеризующие имитостойкость криптосистемы;
·
методы
обеспечения различных уровней имитостойкости.
2.
Приобрести компетенции:
·
обеспечения
совершенной (идеальной) имитостойкости;
·
выбора и
использования основных методов обеспечения имитостойкости криптосистемы.
Содержание темы:
1.
Имитация и подмена сообщения.
2.
Характеристики имитостойкости.
3.
Методы обеспечения имитостойкости шифров.
4.
Совершенная имитостойкость. Коды
аутентификации.
Целостность данных обеспечивается
присоединением к передаваемым данным специального кода (имитовставки),
вырабатываемой по секретному ключу. Имитовставка является разновидностью
контрольной суммы, то есть некоторой эталонной характеристикой сообщения, по
которой осуществляется проверка целостности последнего. Алгоритм формирования
имитовставки должен обеспечивать ее зависимость по некоторому сложному
криптографическому закону от каждого бита сообщения. Проверка целостности
сообщения выполняется получателем сообщения путем выработки по секретному ключу
имитовставки, соответствующей полученному сообщению, и ее сравнения с
полученным значением имитовставки. При совпадении делается вывод о том, что
информация не была модифицирована на пути от отправителя к получателю.
Помимо пассивных
действий со стороны потенциального противника, состоящих в подслушивании или
перехвате передаваемой по каналу связи шифрованной информации, возможны также
его активные действия, состоящие в попытках подмены или имитации
сообщения.
Если передается
шифрованное сообщение у принадлежащее Y (полученное из открытого
текста х принадлежащего X на ключе к принадлежащего К ),
то противник может его заменить на у', отличный от у . При этом
он будет рассчитывать на то, что на действующем ключе к новая
криптограмма при расшифровании будет воспринята как некий осмысленный открытый
текст х', отличный от х. Конечно, это событие может произойти с
некоторой вероятностью, и чем больше эта вероятность, тем успешнее будет
попытка подмены.

Рис. 8.
Попытка имитации может
быть предпринята противником в том случае, когда линия связи готова к работе
(на приеме и передаче установлены действующие ключи), но в рассматриваемый
момент никакого сообщения не передается. В таком случае противник может выбрать
некий у, принадлежащий Y и послать его от имени законного
отправителя. При этом он будет рассчитывать на то, что на действующем ключе его
криптограмма при расшифровании будет воспринята как некий осмысленный открытый
текст. Чем больше вероятность этого события, тем успешнее будет попытка имитации.
При теоретическом исследовании активных действий
противника, его обычно ставят в наиболее благоприятные условия, помещая между
отправителем и получателем, см. рис. 8.
Имитостойкость шифра определяется, как его способность
противостоять попыткам противника по имитации или подмене сообщения.
Наряду с
конфиденциальностью не менее важной задачей является обеспечение целостности
информации, другими словами, — неизменности ее в процессе передачи или хранении.
Решение этой задачи предполагает разработку средств, позволяющих обнаруживать
не столько случайные искажения (для этой цели вполне подходят методы теории
кодирования с обнаружением и исправлением ошибок), сколько целенаправленное
навязывание противником ложной информации. Для этого в передаваемую информацию
вносится избыточность.
Как правило, это
достигается добавлением к сообщению некоторой проверочной комбинации,
вычисляемой с помощью специального алгоритма и играющей роль контрольной суммы
для проверки целостности полученного сообщения. Главное отличие такого метода
от методов теории кодирования состоит в том, что алгоритм выработки проверочной
комбинации является "криптографическим", то есть зависящим от
секретного ключа. Без знания секретного ключа вероятность успешного навязывания
противником искаженной или ложной информации мала. Такая вероятность служит
мерой имитостойкости шифра, то есть способности самого шифра
противостоять активным атакам со стороны противника.
Итак, для проверки
целостности к сообщению М добавляется проверочная комбинация S,
называемая кодом аутентичности сообщения (сокращенно — КАС), или имитовставкой.
В этом случае по каналу связи передается пара С = (М, S) . При
получении сообщения М пользователь вычисляет значение проверочной
комбинации и сравнивает его с полученным контрольным значением S. Несовпадение
говорит о том, что данные были изменены.
Как правило, код
аутентичности сообщения является значением некоторой (зависящей от секретного
ключа) криптографической хэш-функции от данного сообщения: hk(M) = S .
К ключевым хэш-функциям предъявляются определенные требования. К ним относятся:
· невозможность вычисления значения hk(M) = S для
заданного сообщения М без знания ключа к;
· невозможность подбора для заданного сообщения М с
известным значением hk(M) = S другого сообщения Мх с известным
значением hk (М,) = 5, без знания ключа к.
Первое требование
направлено против создания поддельных (сфабрикованных) сообщений при атаках
типа имитация; второе — против модификации передаваемых сообщений при
атаках типа подмена.
Еще один способ борьбы с атаками типа повтор состоит в
модификации исходного сообщения посредством добавления некоторой уникальной
информации: например, порядкового номера сообщения. Использование данного
способа представлено на рис. 9.

Рис. 9.
Коды аутентификации сообщений (Message authentication codes или
MACs) — это следующий базисный элемент, о котором мы поговорим. Они не
обеспечивают секретность, но гарантируют аутентификацию и целостность. Они дают
уверенность, что сообщение пришло именно от того человека, который обозначен
как автор (это аутентификация), и что сообщение по пути не изменилось (а это
целостность).
Вы можете рассматривать MAC как защищающую от вскрытия оболочку
сообщения. Кто угодно может прочесть сообщение — оболочка не обеспечивает
секретность.
Но кто-то, кто знает ключ MAC, может удостовериться, что сообщение
не было изменено. Конкретнее, MAC — это номер, который прикреплен к цифровому
сообщению.
Для MAC применяют секретные ключи совместного использования, типа
симметричных алгоритмов шифрования. Сначала абонент А договаривается о ключе с
абонентом Б. Затем, когда она хочет послать абоненту Б сообщение, она вычисляет
MAC сообщения (применяя секретный ключ) и присваивает его сообщению. У каждого
сообщения есть уникальный MAC для любого возможного ключа.
Когда абонент Б получает сообщение, он вычисляет его MAC
(опять-таки используя все тот же совместный ключ) и сравнивает его с тем
значением MAC, которое прислал абонент А. Если они совпадают, то он может быть
уверен в двух вещах: сообщение действительно пришло от абонента А (или от
кого-то, кто знает секрет общего ключа) — потому что только применяя этот ключ,
можно вычислить MAC, и это сообщение цельное и не измененное — так как MAC
можно вычислить только по полному и точному сообщению. Если бы противник
прослушивал связь, он смог бы прочитать сообщение. Однако если бы он попытался
изменить текст сообщения или MAC, то вычисленный абонентом MAC не был бы равен
тому значению, которое он получил. Противнику пришлось бы изменить сообщение, а
затем изменить MAC, чтобы он был правильным для нового сообщения, но она не
могла бы этого сделать, так как не знает ключа. Банки используют такую простую
систему аутентификации уже несколько десятилетий.
Абонент А может прибегнуть к той же уловке, чтобы установить
подлинность информации, содержащейся в базе данных. Добавляя информацию в базу
данных, он вычисляет MAC и хранит его вместе с информацией. Когда он извлекает
информацию, то снова вычисляет MAC и сравнивает его с тем значением, которое
хранилось в базе данных. Если они совпадают, то он приобретает уверенность, что
никто не изменил информацию.
MAC постоянно используются в Интернете. Их применяют, например, в
протоколе IPsec, чтобы гарантировать, что IP-пакеты не были изменены в
промежутке между отправлением и прибытием на место назначения. Их используют во
всевозможных протоколах межбанковских переводов для установления подлинности
сообщений. Большинство MAC сконструированы с применением симметричных
алгоритмов или односторонних хэш-функций. Например, в СВС-МАС применяется
симметричный алгоритм, а в НМАС и NMAC — хэш-функции.
Кодирование одноразового использования — это самый
простой из всех алгоритмов, его изобрели незадолго до XX века. Основная идея
его состоит в том, что у вас есть набор символов ключа. Вы прибавляете один
символ ключа к каждому символу открытого текста и никогда не повторяете символы
ключа. (Это «одноразовая» часть.) Например, вы прибавляете В (2) к С (3), чтобы
получить Е (5), или Т (20) к L (12), чтобы получить F (6). ((20 + 12) mod 26 =
6.) Такая система подходит для любого алфавита, в том числе и бинарного. И это
единственный имеющийся у нас алгоритм, безопасность которого может быть
доказана.
Вспомним понятие расстояния уникальности. Оно
возрастает при увеличении длины ключа. Когда длина ключа приближается к длине
сообщения, расстояние уникальности стремится к бесконечности. Это означает, что
невозможно восстановить открытый текст, и это доказывает безопасность
одноразового кодирования. Но, с другой стороны, это практически бесполезно.
Поскольку ключ должен при этом быть такой же длины, как и сообщение, то
проблема не решена. Единственный здравый подход к шифрованию должен предполагать,
что очень длинная секретная информация — сообщение — превращается с его помощью
в очень короткую секретную информацию — ключ. При помощи одноразового
кодирования вы нисколько не сокращаете секретную информацию. Так же сложно
доставить шифр получателю, как и доставить само сообщение.
Современная криптография зашифровывает большие
объекты, например цифровые фильмы, соединения через Интернет или телефонные
разговоры, и такое шифрование практически невозможно осуществить, работая с
одноразовым кодированием.
Если утверждают, что некая программа использует этот
алгоритм, то здесь почти наверняка обман. А если и нет, то программа наверняка
непригодна для использования или небезопасна.
1.
А.П. Алферов, А.Ю. Зубов, А.С. Кузьмин, А.В. Черемушкин. Основы криптографии:
Учебное пособие. – М.: Гелиос АРВ, 2005. стр. 45-52.
2.
В.М. Фомичев. Дискретная математика и криптология Курс лекций. – М.:
ДИАЛОГ-МИФИ, 2003. стр. 128-135.
3.
Шаньгин В.Ф. Защита компьютерной информации. Эффективные методы и средства. –
М.: ДМК Пресс, 2008. стр. 140-147.
Цель:
Получить представление о
симметричных системах шифрования, математическом аппарате, лежащем в основе их
функционирования, способах практического применения, сильными и слабыми
сторонами, ознакомиться с основными стандартами симметричных криптографических
систем.
Задачи:
1.
Изучить:
· принцип работы симметричной криптосистемы;
· область применения симметричных систем;
· достоинства и недостатки симметричных криптосистем;
2.
Приобрести компетенции:
· оценки исходных сообщений на предмет криптографического
преобразования с использованием симметричных систем;
· анализа и выбора криптографических систем для
практического использования.
Содержание темы:
1.
Криптографические стандарты. DES, AES.
2.
Алгоритм шифрования данных, определяемый ГОСТ 28147-89.
3.
Достоинства и недостатки симметричных систем шифрования.
Алгоритм шифрования данных DES (Data Encryption Standard) был
опубликован в 1977 году. Блочный симметричный алгоритм DES остается пока распространенным алгоритмом, используемым в
системах защиты коммерческой информации.
Алгоритм DES состоит из чередующейся последовательности перестановок и
подстановок. Алгоритм DES
осуществляет шифрование 64-битовых блоков данных с помощью 64-битового ключа, в
котором значащими являются 56 бит (остальные 8 бит - проверочные биты для
контроля на четность). Обобщенная схема процесса шифрования в блочном алгоритме
DES показана на рис. 10.

Рис. 10. Обобщенная схема шифрования в
алгоритме DES
Процесс шифрования заключается в
начальной перестановке битов 64-битового блока, шестнадцати циклах (раундах)
шифрования и, в заключение, в конечной перестановке битов.
Расшифрование в DES является операцией, обратной шифрованию, и выполняется
путем повторения операций шифрования в обратной последовательности. Основные
достоинства алгоритма DES:
· используется только один ключ
длиной 56 бит;
· относительная простота
алгоритма обеспечивает высокую скорость обработки;
· зашифровав сообщение с помощью
одного пакета программ, для расшифровки можно использовать любой другой пакет
программ, соответствующий алгоритму DES;
· криптостойкость алгоритма
вполне достаточна для обеспечения информационной безопасности большинства
коммерческих приложений.
Современная микропроцессорная техника
позволяет уже сегодня за достаточно приемлемое время взламывать симметричные
блочные шифры с длиной ключа 40 бит. Для такого взламывания используется метод
полного перебора - тотального опробования всех возможных значений ключа (метод
«грубой силы»).
Сегодня все шире используются два
современных криптостойких алгоритма шифрования: отечественный стандарт
шифрования ГОСТ 28147-89 и новый криптостандарт США - AES (Advanced Encryption Standard).
Алгоритм AES не похож на большинство известных алгоритмов симметричного
шифрования, структура которых носит название сети Фейстеля и аналогична
российскому ГОСТ 28147-89. В отличие от отечественного стандарта шифрования,
алгоритм AES
представляет каждый блок обрабатываемых данных в виде двухмерного байтового
массива размером 4x4, 4x6 или 4x8 в зависимости от установленной длины блока
(допускается использование нескольких фиксированных размеров шифруемого блока
информации). Далее на соответствующих этапах производятся преобразования либо
над независимыми столбцами, либо над независимыми строками, либо вообще над
отдельными байтами.
Алгоритм AES состоит из определенного количества раундов (от 10 до 14 -
это зависит от размера блока и длины ключа) и выполняет четыре преобразования:
· BS (ByteSub) - табличная
замена каждого байта массива;
· SR (ShiftRow) - сдвиг строк
массива. При этой операции первая строка остается без изменений, а остальные
циклически побайтно сдвигаются влево на фиксированное число байтов, зависящее
от размера массива.
Например, для массива размером 4x4 строки 2, 3 и 4
сдвигаются соответственно на 1, 2 и 3 байта;
· МС (MixColumn) - операция над
независимыми столбцами массива (рис. 2.11), когда каждый столбец по
определенному правилу умножается на фиксированную матрицу с(х);
· АК (AddRoundKey) - добавление
ключа. Каждый бит массива складывается по модулю 2 с соответствующим битом
ключа раунда, который, в свою очередь, определенным образом вычисляется из
ключа шифрования.
Эти
преобразования воздействуют на массив state, который адресуется с помощью указателя 'state'.
Преобразование AddRoundKey
использует дополнительный указатель для адресации ключа раунда Round Key.
Преобразование BS (ByteSub)
является нелинейной байтовой подстановкой, которая воздействует независимо на
каждый байт массива state,
используя таблицу замен (подстановок) S-box.
В каждом раунде (с некоторыми
исключениями) над шифруемыми данными поочередно выполняются перечисленные
преобразования. Исключения касаются первого и последнего раундов: перед первым
раундом дополнительно выполняется операция АК, а в последнем раунде отсутствует
МС.
Количество раундов шифрования R в
алгоритме AES
переменное (10, 12 или 14 раундов) и зависит от размеров блока и ключа
шифрования (для ключа также предусмотрено несколько фиксированных размеров).
Все преобразования в шифре AES имеют
строгое математическое обоснование. Сама структура и последовательность
операций позволяют выполнять данный алгоритм эффективно как на 8-битовых так и
на 32-битовых процессорах. В структуре алгоритма заложена возможность
параллельного исполнения некоторых операций, что может поднять скорость
шифрования на многопроцессорных рабочих станциях в четыре раза.
Этот алгоритм криптографического
преобразования данных предназначен для аппаратной и программной реализации,
удовлетворяет криптографическим требованиям и не накладывает ограничений на
степень секретности защищаемой информации. Алгоритм шифрования данных,
определяемый ГОСТ 28147-89, представляет собой 64-битовый блочный алгоритм с 256-битовым
ключом.

Рис. 11. Схема алгоритма ГОСТ 28147-89
Данные, подлежащие зашифрованию,
разбивают на 64-разрядные блоки. Эти блоки разбиваются на два субблока N1 и N2 по 32 бит (рис. 11.).
Субблок N1 обрабатывается
определенным образом, после чего его значение складывается со значением
субблока N2
(сложение выполняется по модулю 2, то есть применяется логическая операция XOR -
исключающее ИЛИ), а затем субблоки меняются местами. Данное преобразование
выполняется определенное число раз (раундов): 16 или 32 в зависимости от режима
работы алгоритма.
В каждом раунде выполняются следующие
операции.
Первая операция - наложение ключа.
Содержимое субблока N1 складывается по модулю 232 с 32-битовой частью ключа Кх. Полный
ключ шифрования представляется в виде конкатенации 32-битовых подключей: КО, K1,
К2, КЗ, К4, К5, К6, К7. В
процессе шифрования используется один из этих подключей - в зависимости от
номера раунда и режима работы алгоритма.
Вторая операция - табличная замена. После
наложения ключа субблок N1 разбивается
на 8 частей по 4 бита, значение каждой из которых заменяется в соответствии с
таблицей замены для данной части субблока.
Затем выполняется побитовый циклический
сдвиг субблока влево на 11 бит.
Табличные замены. Блок подстановки S-box (Substitution box) часто используются в современных алгоритмах шифрования,
поэтому стоит пояснить, как организуется подобная операция.
Блок подстановки S-box
состоит из восьми узлов замены (5-блоков замены) S1, S2,S8 с
памятью 64 бит каждый. Поступающий на блок подстановки S 32-битовый
вектор разбивают на восемь последовательно идущих 4-битовых векторов, каждый из
которых преобразуется в 4-битовый вектор соответствующим узлом замены. Каждый
узел замены можно представить в виде таблицы-перестановки шестнадцати 4-битовых
двоичных чисел в диапазоне 0000
- 1111. Входной вектор указывает
адрес строки в таблице, а число в этой строке является выходным вектором. Затем
4-битовые выходные векторы последовательно объединяют в 32-битовый вектор. Узлы
замены (таблицы-перестановки) представляют собой ключевые элементы, которые
являются общими для сети ЭВМ и редко изменяются. Эти узлы замены должны
сохраняться в секрете.
Алгоритм, определяемый ГОСТ 28147-89,
предусматривает четыре режима работы: простой замены, гаммирования, гаммирования
с обратной связью и генерации имитоприставок. В них используется одно и то же
описанное выше шифрующее преобразование, но, поскольку назначение режимов
различно, осуществляется это преобразование в каждом из них по-разному.
В режиме
простой замены для зашифрования
каждого 64-битового блока информации выполняются 32 описанных выше раунда. При
этом 32-битовые подключи используются в следующей последовательности:
· КО, K1, К2, КЗ, К4, К5, Кб,
К7, КО, K1 и т.д. - в раундах с 1-го по 24-й;
· К7, К6, К5, К4, КЗ, К2, K1, КО
- в раундах с 25-го по 32-й;
· Расшифрование в данном режиме
проводится точно так же, но с несколько другой последовательностью применения
подключей;
· КО, K1, К2, КЗ, К4, К5, К6, К7
- в раундах с 1-го по 8-й;
· К7, К6, К5, К4, КЗ, К2, K1,
КО, К7, К6 и т.д. - в раундах с 9-го по 32-й.
Все блоки шифруются независимо друг от
друга, то есть результат зашифрования каждого блока зависит только от его
содержимого (соответствующего блока исходного текста). При наличии нескольких
одинаковых блоков исходного (открытого) текста соответствующие им блоки
шифртекста тоже будут одинаковы, что дает дополнительную полезную информацию
для пытающегося вскрыть шифр криптоаналитика. Поэтому данный режим применяется
в основном для шифрования самих ключей шифрования (очень часто реализуются
многоключевые схемы, в которых по ряду соображений ключи шифруются друг на
друге). Для шифрования собственно информации предназначены два других режима
работы - гаммиования и гаммирования с обратной связью. В режиме гаммирования каждый
блок открытого текста побитно складывается по модулю 2 с блоком гаммы шифра
размером 64 бит. Гамма шифра - это специальная последовательность, которая получается в
результате определенных операций с регистрами N1 и N2:
1.
В
регистры N1 и N2 записывается их начальное заполнение - 64-битовая величина,
называемая синхропосылкой.
2.
Выполняется
зашифрование содержимого регистров N1 и N2 (в данном случае синхропосылки) в режиме простой замены.
3.
Содержимое
регистра N1 складывается по модулю (232 - 1) с константой С1 - 224 +
216 + 28 + 24, а результат сложения записывается в регистр N1.
4.
Содержимое
регистра N2 складывается по модулю 232 с константой С2 = 224 + 216 + 28
+ 1, а результат сложения записывается в регистр N2.
5.
Содержимое
регистров N1 и N2 подается на выход в качестве 64-битового блока гаммы шифра (в
данном случае N1 и N2 образуют первый блок гаммы).
6.
Если
необходим следующий блок гаммы (то есть необходимо продолжить зашифрование или
расшифрование), выполняется возврат к операции 2.
Для расшифрования гамма вырабатывается
аналогичным образом, а затем к битам зашифрованного текста и гаммы снова
применяется операция ХOR. Поскольку эта операция обратима, в случае правильно
выработанной гаммы получается исходный текст
Для выработки нужной для расшифровки
гаммы шифра у пользователя, расшифровывающего криптограмму, должен быть тот же
ключ и то же значение синхропосылки, которые применялись при зашифровании
информации. В противном случае получить исходный текст из зашифрованного не
удастся.
В большинстве реализаций алгоритма ГОСТ
28147-89 синхропосылка не секретна, однако есть системы, где синхропосылка -
такой же секретный элемент, как и ключ шифрования. Для таких систем эффективная
длина ключа алгоритма (256 бит) увеличивается еще на 64 бит секретной
синхропосылки, которую также можно рассматривать как ключевой элемент.
Рассматривая режим генерации имитоприставок, следует определить понятие предмета генерации. Имитоприставка - это
криптографическая контрольная сумма, вычисляемая с использованием ключа
шифрования и предназначенная для проверки целостности сообщений. При генерации
имитоприставки выполняются следующие операции: первый 64-битовый блок массива
информации, для которого вычисляется имитоприставка, записывается в регистры N и N2
зашифровывается в сокращенном режиме простой замены (выполняются первые 16
раундов из 32). Полученный результат суммируется по модулю 2 со следующим
блоком информации с сохранением результата в N1 и N2.
Цикл повторяется до последнего блока
информации. Получившееся в результате этих преобразований 64-битовое содержимое
регистров N1 и N2 или его часть и называется имитоприставкой.
Размер имитоприставки выбирается исходя
из требуемой достоверности сообщений: при длине имитоприставки r бит
вероятность, что изменение сообщения останется незамеченным, равна 2-r.
Чаще всего используется 32-битовая
имитоприставка, то есть половина содержимого регистров. Этого достаточно,
поскольку, как любая контрольная сумма, имитоприставка предназначена, прежде
всего, для защиты от случайных искажений информации. Для защиты же от
преднамеренной модификации данных применяются другие криптографические методы -
в первую очередь электронная цифровая подпись.
При обмене информацией имитоприставка
служит своего рода дополнительным средством контроля. Она вычисляется для открытого
текста при зашифровании какой-либо информации и посылается вместе с
шифртекстом. После расшифрования вычисляется новое значение имитоприставки,
которое сравнивается с присланной. Если значения не совпадают - значит,
шифртекст был искажен при передаче или при расшифровании использовались
неверные ключи. Особенно полезна имитоприставка для проверки правильности
расшифрования ключевой информации при использовании многоключевых схем.
Алгоритм ГОСТ 28147-89 считается очень
стойким - в настоящее время для его раскрытия не предложено более эффективных
методов, чем упомянутый выше метод «грубой силы». Его высокая стойкость
достигается в первую очередь за счет большой длины ключа - 256 бит. При
использовании секретной синхропосылки эффективная длина ключа увеличивается до
320 бит, а засекречивание таблицы замен прибавляет дополнительные биты. Кроме
того, криптостойкость зависит от количества раундов преобразований, которых по
ГОСТ 28147-89 должно быть 32 (полный эффект рассеивания входных данных
достигается уже после 8 раундов).
Алгоритмы симметричного шифрования
используют ключи относительно небольшой длины и могут быстро шифровать большие
объемы данных. При симметричной методологии шифрования отправитель и получатель
применяют для осуществления процессов шифрования и расшифрования сообщения один
и тот же секретный ключ. Алгоритмы симметричного шифрования строятся исходя из
предположения, что зашифрованные данные не сможет прочитать никто из тех, кто
не обладает ключом для их расшифрования. Если ключ не был скомпрометирован, то
при расшифровании автоматически выполняется аутентификация отправителя, так как
только отправитель имеет ключ, с помощью которого можно зашифровать информацию,
и только получатель имеет ключ, позволяющий расшифровать информацию.
Алгоритмы симметричного шифрования
применяются для абонентского шифрования данных - то есть для шифрования
информации, предназначенной для отправки кому-либо, например, через Интернет.
Использование только одного секретного ключа для всех абонентов сети, конечно,
недопустимо по соображениям безопасности: в случае компрометации (утери,
хищения) ключа под угрозой будет находиться документооборот всех абонентов
сети.
Порядок использования систем с симметричными
ключами:
1.
Симметричный
секретный ключ должен создаваться, распространяться и сохраняться безопасным
образом.
2.
Для
получения зашифрованного текста отправитель применяет к исходному сообщению
симметричный алгоритм шифрования вместе с секретным симметричным ключом. Таким образом,
неявно подготавливается аутентификация отправителя и получателя, так как только
отправитель знает симметричный секретный ключ и может зашифровать этот текст.
Только получатель знает симметричный секретный ключ и может расшифровать этот
текст.
3.
Отправитель
передает зашифрованный текст. Симметричный секретный ключ никогда не передается
в открытой форме по незащищенным каналам связи.
4.
Получатель
применяет к зашифрованному тексту тот же самый симметричный алгоритм
шифрования/расшифрования вместе с тем же самым симметричным ключом (который уже
есть у получателя) для восстановления исходного текста. Его успешное
восстановление аутентифицирует того, кто знает секретный ключ.
Для симметричных криптосистем актуальна
проблема безопасного распределения симметричных секретных ключей. Всем системам
симметричного шифрования присущи следующие недостатки:
· принципиальным является
требование защищенности и надежности канала передачи секретного ключа для
каждой пары участников информационного обмена;
· предъявляются повышенные
требования к службе генерации и распределения ключей, обусловленные тем, что
для N абонентов при схеме взаимодействия «каждый с каждым» требуется Nх(N- 1) /
2 ключей, то есть зависимость числа ключей от числа абонентов является квадратичной;
например, для п = 1000 абонентов требуемое количество ключей будет равно
1000х(1000-1)/2 = 499 500 ключей.
Поэтому без эффективной организации
защищенного распределения ключей широкое использование обычной системы
симметричного шифрования в больших сетях и, в частности, в глобальных сетях
практически невозможно.
1.
А.П. Алферов, А.Ю. Зубов, А.С. Кузьмин, А.В. Черемушкин. Основы криптографии:
Учебное пособие. – М.: Гелиос АРВ, 2005. стр. 52-59.
2.
В.М. Фомичев. Дискретная математика и криптология Курс лекций. – М.:
ДИАЛОГ-МИФИ, 2003. стр. 135-143.
3.
Шаньгин В.Ф. Защита компьютерной информации. Эффективные методы и средства. –
М.: ДМК Пресс, 2008. стр. 147-154.
Цель:
Получить представление об
асимметричных системах шифрования, математическом аппарате, лежащем в основе их
функционирования, способах практического применения, сильными и слабыми
сторонами, ознакомиться с основными стандартами открытых криптографических
систем.
Задачи:
1.
Изучить:
· принцип работы криптосистемы с открытым ключом;
· область применения асимметричных систем;
· достоинства и недостатки асимметричных криптосистем;
2.
Приобрести компетенции:
· генерации открытых и закрытых ключей асимметричной
криптосистемы;
· анализа и выбора криптографических систем для
практического использования.
Содержание темы:
1.
Понятие односторонней функции и односторонней функции с "лазейкой". Проблемы
факторизации целых чисел.
2.
Криптосистема RSA.
3.
Достоинства и недостатки асимметричных систем шифрования.
Асимметричные криптографические системы были
разработаны в 1970-х годах. Принципиальное отличие асимметричной криптосистемы
от криптосистемы симметричного шифрования состоит в том, что для шифрования
информации и ее последующего расшифрования используются различные ключи:
· открытый ключ К: используется для шифрования информации, вычисляется из секретного ключа
k;
· секретный ключ k: используется
для расшифрования информации, зашифрованной с помощью парного ему открытого ключа
К.
Эти ключи различаются таким образом, что с помощью
вычислений нельзя вывести секретный ключ k из
открытого ключа К. Поэтому открытый ключ К может свободно
передаваться по каналам связи.
Асимметричные системы называют еще двухключевыми
криптографическими системами или криптосистемами с открытым ключом.
Обобщенная схема асимметричной криптосистемы
шифрования с открытым ключом показана на рис. 12.

Рис. 12. Обобщенная схема асимметричной
криптосистемы шифрования
Для криптографического закрытия и последующего
расшифрования передаваемой информации используются открытый и секретный ключи
получателя В сообщения. В качестве ключа зашифрования
должен использоваться открытый ключ получателя, а в качестве ключа
расшифрования - его секретный ключ.
Секретный и открытый ключи генерируются попарно.
Секретный ключ должен оставаться у его владельца; он должен быть надежно
защищен от несанкционированного доступа (аналогично ключу шифрования в
симметричных алгоритмах). Копия открытого ключа должна иметься у каждого абонента
криптографической сети, с которым обменивается информацией владелец секретного
ключа. Процесс передачи зашифрованной информации в асимметричной криптосистеме
осуществляется следующим образом:
1.Подготовительный
этап.
Абонент В
генерирует пару ключей: секретный ключ kB и
открытый ключ КВ.
Открытый ключ КВ
посылается абоненту А и остальным абонентам (или
делается доступным, например, на разделяемом ресурсе).
2.Использование
- обмен информацией между абонентами А
и В. Абонент А зашифровывает
сообщение с помощью открытого ключа КВ
абонента В и
отправляет шифртекст абоненту В.
Абонент В расшифровывает сообщение с помощью
своего секретного ключа kB. Никто
другой (в том числе абонент А) не
может расшифровать данное сообщение, так как не имеет секретного ключа абонента
В. Защита информации в асимметричной криптосистеме основана на
секретности ключа kB получателя
сообщения.
Отметим характерные особенности асимметричных
криптосистем:
1. Открытый ключ КВ
и криптограмма С могут
быть отправлены по незащищенным каналам, то есть противнику известны КВ и С.
2. Алгоритмы шифрования и расшифрования:
1) ЕВ
: М → С,
2) DB: С → М.
являются открытыми.
У. Диффи и М. Хеллман сформулировали требования,
выполнение которых обеспечивает безопасность асимметричной криптосистемы:
1. Вычисление пары ключей (КВ, kB) получателем
В на основе начального
условия должно быть простым.
2. Отправитель А,
зная открытый ключ КВ
и сообщение М, может легко вычислить криптограмму:
1) С=ЕКВ(М).
3. Получатель В, используя секретный ключ kB и
криптограмму С, может легко восстановить исходное сообщение:
1)
M = DkВ(C).
4. Противник, зная открытый ключ КВ, при попытке вычислить секретный ключ kB наталкивается
на непреодолимую вычислительную проблему.
5.
Противник, зная пару (КВ,
С), при попытке вычислить
исходное сообщение М наталкивается
на непреодолимую вычислительную проблему.
Концепция асимметричных криптографических систем с
открытым ключом основана на применении однонаправленных функций.
Неформально однонаправленную функцию можно
определить следующим образом. Пусть X
и Y- некоторые произвольные множества. Функция f:X→Y является однонаправленной,
если для всех х принадлежит
X можно легко
вычислить функцию:
у =f(x), где y принадлежит Y.
И в то же время для большинства у принадлежащих
Y достаточно сложно получить значение х принадлежащее X,
такое, что f(x) = у
(при этом полагают, что существует по
крайней мере одно такое значение х.
Основным критерием отнесения функции к классу
однонаправленных функций является отсутствие эффективных алгоритмов обратного
преобразования Y →X.
В качестве примера однонаправленной функции можно
указать целочисленное умножение. Прямая задача - вычисление произведения
двух очень больших целых чисел Р и Q, то есть
нахождение значения:
N=PxQ
является относительно несложной задачей для
компьютера.
Обратная задача - факторизация, или разложение на
множители большого целого числа, то есть нахождение делителей Р и Q большого целого числа N=Р х Q является
практически неразрешимой задачей при достаточно больших значениях N. По
современным оценкам теории чисел, при целом N = 2664
и Р~ Q для разложения числа N потребуется около 1023
операций, то есть задача практически неразрешима для современных компьютеров.
Другой характерный пример однонаправленной функции -
это модульная экспонента с фиксированными основанием и модулем. Пусть А и N - целые числа, такие, что 1 < А < N. Определим
множество ZN:
ZN={0, 1,2,
... N - 1}.
Тогда модульная экспонента с основанием А по
модулю N представляет собой функцию:
fa.n-:ZN →ZN
fa.n {x) = Ax(modN),
где X -
целое число, 1 < х < N - 1.
Существуют эффективные алгоритмы, позволяющие
достаточно быстро вычислить значения функции fa.n {x).
Если у = Ах,
то естественно записать х = logA(y).
Поэтому задачу обращения функции fa.n(x) называют задачей нахождения дискретного логарифма, или
задачей дискретного логарифмирования.
Задача дискретного логарифмирования формулируется следующим образом. Для известных целых A, N,
у найти целое число х, такое,
что:
Aх mod N = у.
Алгоритм вычисления дискретного логарифма за
приемлемое время пока не найден. Поэтому модульная экспонента считается
однонаправленной функцией. По современным оценкам теории чисел, при целых
числах А = 2664 и N= 2664 решение задачи
дискретного логарифмирования (нахождение показателя степени х для
известного у) потребует около 1026 операций, то есть эта
задача имеет в 103 раз большую вычислительную сложность, чем задача
разложения на множители. При увеличении длины чисел разница в оценках сложности
задач возрастает.
Следует отметить, что пока не удалось доказать
невозможность существования эффективного алгоритма вычисления дискретного
логарифма за приемлемое время. Исходя из этого модульная экспонента отнесена к
однонаправленным функциям условно, что, однако, не мешает с успехом применять
ее на практике.
Вторым важным классом функций, используемых при
построении криптосистем с открытым ключом, являются так называемые однонаправленные
функции с секретом. Дадим неформальное определение такой функции. Функция
f:X→Y
относится к классу однонаправленных функций с секретом
в том случае, если она является однонаправленной и, кроме того, возможно
эффективное вычисление обратной функции, если известен секрет (секретное
число, строка или другая информация, ассоциируемая с данной функцией).
В качестве примера однонаправленной функции с секретом
можно указать используемую в криптосистеме RSA модульную экспоненту с фиксированными модулем и
показателем степени. Переменное основание модульной экспоненты используется для
представления числового значения сообщения М либо криптограммы.
Как и в случае симметричных криптографических систем,
с помощью асимметричных криптосистем обеспечивается не только
конфиденциальность, но также подлинность и целостность передаваемой информации.
Подлинность и целостность любого сообщения обеспечивается формированием
цифровой подписи этого сообщения и отправкой в зашифрованном виде сообщения
вместе с цифровой подписью. Проверка соответствия подписи полученному сообщению
после его предварительного расшифровывания представляет собой проверку
целостности и подлинности принятого сообщения.
Криптоалгоритм RSA предложили в 1978 году три автора: Р. Райвест (Rivest), А. Шамир (Shamir) и
А. Адлеман (Adleman). Алгоритм получил свое
название по первым буквам фамилий его авторов. Алгоритм RSA стал первым алгоритмом с открытым ключом, который
может работать в режиме как шифрования данных, так и электронной цифровой
подписи.
Надежность алгоритма RSA основывается на трудности факторизации больших чисел
и сложности вычисления дискретных логарифмов в конечном поле.
В алгоритме RSA
открытый ключ КВ,
секретный ключ kB, сообщение М и криптограмма С принадлежат множеству целых
чисел:
ZN ={0,
1,2, ...,N- 1},
где N - модуль:
N = PxQ.
Здесь Р и Q - случайные
большие простые числа. Для обеспечения максимальной безопасности выбирают Р
и Q равной
длины и хранят в секрете.
Множество ZN с
операциями сложения и умножения по модулю N
образует арифметику по модулю N.
Открытый ключ КВ выбирают случайным
образом так, чтобы выполнялись следующие условия:
1 < КB ≤ φ (N), НОД(КВ, φ (N) = 1,
φ (N) = (P- l)(Q-1),
где φ (N)- функция Эйлера.
Функция Эйлера φ (N) указывает
количество положительных целых чисел в интервале от 1 до N, которые
взаимно просты с N.
Второе из указанных выше условий означает, что
открытый ключ Кв и функция Эйлера φ (N) должны быть
взаимно простыми.
Далее, используя расширенный алгоритм Евклида,
вычисляют секретный ключ kB, такой, что:
kB x KB≡l(mod φ (N))
или
kB = KB-1(mod (Р-1)(Q-1)).
Это можно осуществить, так как получатель В знает
пару простых чисел (Р, Q) и может легко
найти φ(N). Заметим, что
kB и
N должны быть взаимно простыми.
Открытый ключ КB используют
для шифрования данных, а секретный ключ kB -для
расшифрования.
Процедура шифрования определяет криптограмму С через
пару (открытый ключ КB, сообщение М) в соответствии
со следующей формулой:
C
= EKB(M) = MKB(modN).
В качестве алгоритма быстрого вычисления значения С
используют ряд последовательных возведений в квадрат целого М и
умножений на М с приведением по модулю N.
Расшифрование криптограммы С выполняют,
используя пару (секретный ключ kB, криптограмма
С) по следующей формуле:
M = DkB (C) = CkB(modN).
Процедуры шифрования и расшифрования в алгоритме RSA рассмотрим на примере шифрования сообщения CAB. Для простоты вычислений будут использоваться
небольшие числа. На практике применяются очень большие числа (длиной 250-300
десятичных разрядов).
Действия
пользователя В:
1.
Выбирает Р=3 и Q=11.
2.
Вычисляет модуль N=Р х Q=Зх11=33.
3.
Вычисляет значение функции Эйлера для N
= 33:
φ (N) = φ (33) = (Р- 1)(Q- 1) = 2 х 10 = 20.
Выбирает в качестве открытого ключа КВ произвольное
число с учетом выполнения условий:
1<КВ< 20, НОД (КВ, 20) = 1.
Пусть КВ = 7.
Вычисляет значение секретного ключа kB, используя
расширенный алгоритм Евклида при решении сравнения
kB = 7-1(mod 20) или
КВ х kB mod(Р- 1)(Q- 1) =1.
Решение дает kB = 3.
4.
Пересылает пользователю А пару чисел (N=33,KB = 7).
Действия пользователя А:
5. Представляет шифруемое сообщение как
последовательность целых чисел в диапазоне 0-32. Пусть буква А представляется
как число 1, буква В - как число 2, буква С - как число 3. Тогда сообщение CAB можно представить как последовательность чисел 312,
то есть М1 =
6. Шифрует текст, представленный в виде
последовательности чисел Ми М2 и М3,
используя ключ Кв = 7 и N = 33, по формуле:
Сi = MiKB (mod N) = Mi7(mod
33).
Получает:
С1= 37(mod 33) = 2187(mod 33) =
9,
С2 = l7(mod 33) = l(mod 33) = 1,
С3 = 27(mod 33) = 128(mod 33) =
29.
Отправляет пользователю В криптограмму:
С1 С2, С3 = 9, 1, 29.
Действия пользователя В:
7. Расшифровывает принятую криптограмму С1 С2,
С3, используя секретный ключ kB =
3, по формуле:
Мi = CiKB(mod N) = Ci3(mod
33).
Получает:
М1 = 93(mod 33) = 729(mod 33) =
3,
М2 = l3(mod 33) = l(mod 33) = 1,
М3 =
293(mod 33) - 24389(mod 33) = 2.
Таким образом, восстановлено исходное сообщение CAB: 312.
Криптоалгоритм RSA всесторонне исследован и признан стойким при
достаточной длине ключей. В настоящее время длина ключа 1024 бит считается
приемлемым вариантом. Некоторые авторы утверждают, что с ростом мощности
процессоров криптоалгоритм RSA потеряет
стойкость к атаке полного перебора. Однако увеличение мощности процессоров
позволит применять более длинные ключи, что повышает стойкость RSA Следует отметить, что алгоритм RSA можно применять как для шифрования сообщений, так и
для электронной цифровой подписи.
Нетрудно видеть, что в асимметричной криптосистеме RSA количество используемых ключей связано с количеством
абонентов линейной зависимостью (в системе из N пользователей используется 2
х N ключей), а не
квадратической, как в симметричных системах.
Асимметричные криптографические системы обладают
следующими важными преимуществами перед симметричными криптосистемами:
· в асимметричных криптосистемах
решена сложная проблема распределения ключей между пользователями, так как
каждый пользователь может сгенерировать свою пару ключей сам, а открытые ключи
пользователей могут свободно публиковаться и распространяться по сетевым
коммуникациям;
· исчезает квадратическая
зависимость числа ключей от числа пользователей; в асимметричной криптосистеме
количество используемых ключей связано с количеством абонентов линейной
зависимостью (в системе из N пользователей используется 2N ключей), а не
квадратической, как в симметричных системах;
· асимметричные криптосистемы
позволяют реализовать протоколы взаимодействия сторон, которые не доверяют друг
другу, поскольку при использовании асимметричных криптосистем закрытый ключ
должен быть известен только его владельцу.
Однако у асимметричных криптосистем существуют и
недостатки:
· на настоящий момент нет
математического доказательства необратимости используемых в асимметричных
алгоритмах функций;
· по сравнению с симметричным
шифрованием, асимметричное существенно медленнее, поскольку при шифровании и
расшифровке используются весьма ресурсоемкие операции. По этой же причине
реализовать аппаратный шифратор с асимметричным алгоритмом существенно сложнее,
чем аппаратно симметричный алгоритм;
· необходимо защищать открытые
ключи от подмены.
1.
А.П.Алферов, А.Ю.Зубов, А.С.Кузьмин, А.В.Черемушкин. Основы криптографии:
Учебное пособие. – М.: Гелиос АРВ, 2005. стр. 59-69.
2.
В.М. Фомичев. Дискретная математика и криптология Курс лекций. – М.:
ДИАЛОГ-МИФИ, 2003. стр. 143-150.
3.
Шаньгин В.Ф. Защита компьютерной информации. Эффективные методы и средства. –
М.: ДМК Пресс, 2008. стр. 154-162.
Цель:
Получить представление о
принципах криптографического преобразования информации, обеспечивающих ведение
электронного документа. Ознакомиться с основными действующими стандартами,
реализующими данные принципы.
Задачи:
1.
Изучить:
·
способы
преобразования информации, используемые при создании хэш-образов сообщений;
·
формы и способы
деструктивных действий неавторизованных лиц по отношению к электронным
документам;
·
порядок
формирования и проверки электронной цифровой подписи.
2. Приобрести компетенции:
·
использования действующих
стандартов хэширования;
·
использования
действующих стандартов цифровой подписи.
Содержание темы:
1.
Криптографические хэш-функции. Характеристики и алгоритмы выработки
хэш-функций.
2.
Хэширование по алгоритму ГОСТ Р 34.11-94.
3.
Понятие электронной цифровой подписи. Стандарты электронной цифровой подписи.
4.
Стандарт цифровой подписи ГОСТ Р 34.10-94.
Функция
хэширования (хэш-функция) представляет собой преобразование, на вход которого
подается сообщение переменной длины М, а выходом является строка фиксированной
длины h(M). Иначе говоря, хэш-функция h(.)
принимает
в качестве аргумента сообщение (документ) М произвольной длины и
возвращает хэш-значение (хэш) Н= h(M) фиксированной длины (рис. 13.).
Хэш-значение h(M)
- это дайджест сообщения М, то есть сжатое двоичное
представление основного сообщения М произвольной длины. Хэш-значение h(M) формируется функцией
хэширования.
Функция хэширования позволяет сжать подписываемый документ М до 128 бит и более (в
частности, 128 или 256 бит), тогда как М может быть размером в мегабайт или более. Следует
отметить, что значение хэш-функции h(M) зависит сложным образом от
документа М и не позволяет восстановить сам документ М.
Функция
хэширования должна обладать следующими свойствами:
1. Хэш-функция может быть
применена к аргументу любого размера.
2. Выходное значение хэш-функции
имеет фиксированный размер.

Рис. 13. Схема формирования H=h(M)
3. Хэш-функцию h(x) достаточно просто вычислить
для любого х.
Скорость
вычисления хэш-функции должна быть такой, чтобы скорость выработки и проверки
ЭЦП при использовании хэш-функции была значительно больше, чем при
использовании самого сообщения.
4. Хэш-функция должна быть
чувствительна к всевозможным изменениям в тексте М, таким как вставки, выбросы,
перестановки и т.п.
5. Хэш-функция должна быть
однонаправленной, то есть обладать свойством необратимости. Иными словами,
задача подбора документа M’, который обладал бы требуемым
значением хэш-функции, должна быть вычислительно неразрешима.
6. Вероятность того, что значения
хэш-функций двух различных документов (вне зависимости от их длин) совпадут,
должна быть ничтожно мала; то есть для любого фиксированного х с вычислительной точки зрения
невозможно найти х x’ ≠ х, такое что h(x)
= h(x).
Теоретически возможно, что два различных сообщения могут быть сжаты в
одну и ту же свертку (так называемая коллизия, или столкновение). Поэтому для
обеспечения стойкости функции хэширования необходимо предусмотреть способ
избегать столкновений. Полностью столкновений избежать нельзя, поскольку в
общем случае количество возможных сообщений превышает количество возможных
выходных значений функции хэширования. Однако вероятность столкновения должна
быть низкой.
Свойство 5 эквивалентно тому, что h(x)
является односторонней функцией. Свойство 6 гарантирует, что не может быть
найдено другое сообщение, дающее ту же свертку. Это предотвращает фальсификацию
сообщения.
Таким образом, функция хэширования может использоваться для обнаружения
изменений сообщения, то есть она может служить для формирования криптографической контрольной
суммы (также
называемой кодом обнаружения изменений или кодом аутентификации
сообщения). В
этом качестве хэш-функция используется для контроля целостности сообщения, при
формировании и проверке электронной цифровой подписи.
Хэш-функции широко
используются также в целях аутентификации пользователей. В ряде технологий
информационной безопасности применяется своеобразный прием шифрования - шифрование с помощью
односторонней хэш-функции. Своеобразие этого шифрования заключается в том, что
оно, по существу, является односторонним, то есть не сопровождается обратной
процедурой - расшифрованием на приемной стороне. Обе стороны (отправитель и
получатель) используют одну и ту же процедуру одностороннего шифрования на
основе хэш-функции.

Рис. 14.
Хэширование по алгоритму ГОСТ Р 34.11-94
Отечественным
стандартом генерирования хэш-функции является алгоритм ГОСТ Р 34.11-94. Этот
стандарт является обязательным для применения в качестве алгоритма хэширования
в государственных организациях РФ и ряде коммерческих организаций. Коротко
данный алгоритм хэширования можно описать следующим образом (рис. 14.).
Шаг 1. Инициализация регистра
хэш-значения. Если длина сообщения не превышает 256 бит - переход к шагу 3,
если превышает - переход к шагу 2.
Шаг 2. Итеративное вычисление
хэш-значения блоков хэшируемых данных по 256 бит с использованием хранящегося в
регистре хэш-значения предыдущего блока. Вычисление включает в себя следующие
действия:
· генерацию ключей шифрования на
основе блока хэшируемых данных;
· зашифрование хранящегося в
регистре хэш-значения в виде четырех блоков по 64 бит по алгоритму ГОСТ
28147-89 в режиме простой замены;
· перемешивание результата.
Вычисление производится до тех пор, пока длина необработанных входных
данных не станет меньше или равной 256 бит. В этом случае - переход к шагу 3.
Шаг 3. Дополнение слева битовыми
нулями необработанной части сообщения до 256 бит. Вычисление хэш-значения
аналогично шагу 2. В результате в регистре оказывается искомое хэш-значение.
Электронная цифровая подпись используется для аутентификации
текстов, передаваемых по телекоммуникационным каналам. При таком обмене
электронными документами существенно снижаются затраты на обработку и хранение
документов, ускоряется их поиск. Но возникает проблема аутентификации автора
электронного документа и самого документа, то есть установления подлинности
автора и отсутствия изменений в полученном электронном документе.
Целью аутентификации электронных документов является
их защита от возможных видов злоумышленных действий, к которым относятся:
· активный перехват -
нарушитель, подключившийся к сети, перехватывает документы (файлы) и изменяет
их;
· маскарад - абонент С посылает
документ абоненту В от имени абонента А;
· ренегатство - абонент А
заявляет, что не посылал сообщения абоненту В, хотя на самом деле послал;
· подмена - абонент В изменяет
или формирует новый документ и заявляет, что получил его от абонента А;
· повтор - абонент С повторяет
ранее переданный документ, который абонент А посылал абоненту В.
Эти виды злоумышленных действий могут нанести существенный
ущерб банковским и коммерческим структурам, государственным предприятиям и
организациям, частным лицам, применяющим в своей деятельности компьютерные
информационные технологии.
Проблему проверки целостности сообщения и подлинности
автора сообщения позволяет эффективно решить методология электронной цифровой
подписи.
Основные процедуры цифровой подписи.
Функционально цифровая подпись аналогична обычной
рукописной подписи и обладает ее основными достоинствами:
· удостоверяет, что подписанный
текст исходит от лица, поставившего подпись;
· не дает самому этому лицу
возможности отказаться от обязательств, связанных с подписанным текстом;
· гарантирует целостность
подписанного текста.
Электронная цифровая подпись (ЭЦП) представляет собой
относительно небольшое количество дополнительной цифровой информации,
передаваемой вместе с подписываемым текстом. ЭЦП основана на обратимости
асимметричных шифров, а также на взаимосвязанности содержимого сообщения, самой
подписи и пары ключей. Изменение хотя бы одного из этих элементов сделает
невозможным подтверждение подлинности цифровой подписи. ЭЦП реализуется при
помощи асимметричных алгоритмов шифрования и хэш-функций.
Технология применения системы ЭЦП предполагает наличие
сети абонентов, посылающих друг другу подписанные электронные документы. Для
каждого абонента генерируется пара ключей: секретный и открытый. Секретный ключ
хранится абонентом в тайне и используется им для формирования ЭЦП. Открытый
ключ известен всем другим пользователям и предназначен для проверки ЭЦП
получателем подписанного электронного документа.
Система ЭЦП включает две основные процедуры:
· процедуру формирования
цифровой подписи;
· процедуру проверки цифровой
подписи.
В процедуре формирования подписи используется
секретный ключ отправителя сообщения, в процедуре проверки подписи - открытый
ключ отправителя.
Процедура формирования цифровой подписи.
На
подготовительном этапе этой процедуры абонент А - отправитель сообщения -
генерирует пару ключей: секретный ключ kA и открытый ключ КА. Открытый ключ КА вычисляется из парного ему
секретного ключа kA. Открытый ключ КА рассылается остальным
абонентам сети (или делается доступным, например, на разделяемом ресурсе) для
использования при проверке подписи.
Для
формирования цифровой подписи отправитель А прежде всего вычисляет
значение хэш-функции h(M) подписываемого текста М (рис. 15.). Хэш-функция служит
для сжатия исходного подписываемого текста М в дайджест т - относительно короткое число,
состоящее из фиксированного небольшого числа битов и характеризующее весь текст
М в целом. Далее отправитель А шифрует дайджест т своим секретным ключом kA. Получаемая при этом пара чисел представляет собой
цифровую подпись для данного текста М. Сообщение М вместе с цифровой подписью отправляется в адрес
получателя.
Процедура проверки цифровой подписи.
Абоненты
сети могут проверить цифровую подпись полученного сообщения М с помощью открытого ключа
отправителя КА
этого
сообщения (рис. 16.).
При проверке ЭЦП абонент В - получатель сообщения М - расшифровывает принятый дайджест
т открытым ключом КА отправителя А. Кроме того, получатель сам
вычисляет с помощью хэш-функции h(M) дайджест т принятого сообщения Ми
сравнивает его с расшифрованным. Если эти два дайджеста –т и т'
-совпадают,
то цифровая подпись является подлинной. В противном случае либо подпись
подделана, либо изменено содержание сообщения.
Принципиальным моментом в системе ЭЦП является невозможность подделки
ЭЦП пользователя без знания его секретного ключа подписывания. Поэтому
необходимо защитить секретный ключ подписывания от несанкционированного
доступа. Секретный ключ ЭЦП, аналогично ключу симметричного шифрования,
рекомендуется хранить на персональном ключевом носителе в защищенном виде.

Рис. 15.
Схема формирования электронной цифровой подписи

Рис. 16.
Схема проверки электронной цифровой подписи
Электронная цифровая подпись представляет собой уникальное число,
зависящее от подписываемого документа и секретного ключа абонента. В качестве
подписываемого документа может быть использован любой файл. Подписанный файл
создается из неподписанного путем добавления в него одной или более электронных
подписей.
Помещаемая в подписываемый файл (или в отдельный файл электронной
подписи) структура ЭЦП обычно содержит дополнительную информацию, однозначно
идентифицирующую автора подписанного документа. Эта информация добавляется к
документу до вычисления ЭЦП, что обеспечивает и ее целостность. Каждая подпись
содержит следующую информацию:
· дату подписи;
· срок окончания действия ключа
данной подписи;
· информацию о лице, подписавшем
файл (Ф.И.О., должность, краткое наименование фирмы);
· идентификатор подписавшего
(имя открытого ключа);
· собственно цифровую подпись.
Важно отметить, что, с точки зрения конечного пользователя, процесс
формирования и проверки цифровой подписи отличается от процесса
криптографического закрытия передаваемых данных следующими особенностями.
При формировании цифровой подписи используется закрытый ключ
отправителя, тогда как при зашифровании применяется открытый ключ получателя.
При проверке цифровой подписи используется открытый ключ отправителя, а при
расшифровывании - закрытый ключ получателя.
Проверить сформированную подпись может любое лицо, так как ключ
проверки подписи является открытым. При положительном результате проверки
подписи делается заключение о подлинности и целостности полученного сообщения,
то есть о том, что это сообщение действительно отправлено тем или иным
отправителем и не было модифицировано при передаче по сети. Однако, если
пользователя интересует, не является ли полученное сообщение повторением ранее
отправленного или не было ли оно задержано на пути следования, то он должен
проверить дату и время его отправки, а при наличии - порядковый номер.
Аналогично асимметричному шифрованию, необходимо обеспечить
невозможность подмены открытого ключа, используемого для проверки ЭЦП. Если
предположить, что злоумышленник п имеет доступ к открытым ключам, которые хранит на
своем компьютере абонент В, в том числе к открытому ключу КА абонента А, то он может
выполнить следующие действия:
· прочитать из файла, в котором
содержится открытый ключ КА, идентификационную информацию об
абоненте А;
· сгенерировать собственную пару
ключей kn и Кn, записав в них
идентификационную информацию абонента A;
· подменить хранящийся у
абонента В открытый ключ КА своим открытым ключом Кn, но
содержащим идентификационную информацию абонента A.
После этого злоумышленник п может посылать документы абоненту В, подписанные своим секретным
ключом kn. При проверке подписи этих
документов абонент В будет считать, что документы подписаны абонентом A и
их ЭЦП верна, то есть они не были модифицированы кем-либо. До выяснения
отношений непосредственно с абонентом А у абонента В может не появиться сомнений в
полученных документах. Открытые ключи ЭЦП можно защитить от подмены с помощью
соответствующих цифровых сертификатов.
Первый отечественный стандарт цифровой подписи обозначается как ГОСТ Р
34.10-94. Алгоритм цифровой подписи, определяемый этим стандартом,
концептуально близок к алгоритму DSA В нем используются следующие
параметры:
· р - большое простое число длиной
от 509 до 512 бит либо от 1020 до 1024 бит;
· q - простой сомножитель числа (р - 1), имеющий длину 254-256
бит;
· а - любое число, меньшее (р - 1), причем такое, что aq
mod р = 1;
· х - некоторое число, меньшее q;
· у = ах mod р.
Кроме того, этот алгоритм использует однонаправленную хэш-функцию H(х). Стандарт ГОСТ Р 34.11-94
определяет хэш-функцию, основанную на использовании стандартного симметричного
алгоритма ГОСТ 28147-89.
Первые три параметра -p,q и a- являются открытыми и могут
быть общими для всех пользователей сети. Число х является секретным ключом.
Число у является открытым ключом.
Чтобы подписать некоторое сообщение т, а затем проверить подпись,
выполняются следующие шаги:
1. Пользователь А генерирует случайное число k, причем k
< q.
2.
Пользователь А вычисляет значения:
r = (аk mod р) mod q,
s = (х х r +
k(H(m))) mod
q.
Если H(m) mod q = 0, то значение H(m) mod q принимают равным единице.
Если r = 0, то выбирают другое значение
k и начинают снова.
Цифровая подпись представляет собой два числа:
r mod
2256 и s mod
2256.
Пользователь А отправляет эти числа пользователю В.
3. Пользователь В проверяет полученную подпись,
вычисляя:
v = Н(тп)q-2
mod q,
z1
= (s ∙ v) mod q,
z2 = ((q
- r) ∙ v) mod q,
u = ((az1 ∙ yz2) mod p) mod
q.
Если u = r, то подпись считается верной.
Различие
между этим алгоритмом и алгоритмом DSA заключается в том, что в DSA:
s - (k-1(x∙r
+ (H(m)))) mod
q,
что приводит к другому уравнению верификации.
Следует также отметить, что в отечественном стандарте ЭЦП параметр q имеет длину 256 бит. Западных криптографов вполне
устраивает q длиной примерно 160 бит.
Различие в значениях параметра q является отражением стремления
разработчиков отечественного стандарта к получению более безопасной подписи.
Этот стандарт вступил в действие с начала 1995 года.
Отечественный стандарт цифровой подписи ГОСТ Р 34.10-2001.
Отечественный
стандарт цифровой подписи ГОСТ Р 34.10-2001 был принят в 2001 году [12]. Этот
стандарт разработан взамен первого стандарта цифровой подписи ГОСТ Р 34.10-94.
Необходимость разработки стандарта ГОСТ Р 34.10-2001 вызвана потребностью в
повышении стойкости электронной цифровой подписи к несанкционированным
изменениям. Стойкость ЭЦП основывается на сложности вычисления дискретного
логарифма в группе точек эллиптической кривой, а также на стойкости
используемой хэш-функции по ГОСТ Р 34.11.
1.
А.П.Алферов, А.Ю.Зубов, А.С.Кузьмин, А.В.Черемушкин. Основы криптографии:
Учебное пособие. – М.: Гелиос АРВ, 2005. стр. 69-78.
2.
В.М. Фомичев. Дискретная математика и криптология Курс лекций. – М.:
ДИАЛОГ-МИФИ, 2003. стр. 150-161.
3.
Шаньгин В.Ф. Защита компьютерной информации. Эффективные методы и средства. –
М.: ДМК Пресс, 2008. стр. 162-171.
Цель:
Рассмотреть
криптографический протокол, как основной обязательный регламент действий
участников информационного обмена, позволяющий обеспечить безопасность
информационных ресурсов.
Задачи:
1.
Изучить:
·
основные типы
криптографических протоколов;
·
критерии
классификации криптографических протоколов;
·
принципы
открытого распределения ключей.
2.
Приобрести компетенции:
·
классификации и
выбора криптографических протоколов;
·
формирования
исходных данных для организации защищенной связи.
Содержание темы:
1.
Понятие криптографического протокола. Основные примеры.
2.
Классификация криптографических протоколов. Протоколы сертификации ключей.
3.
Протоколы предварительного распределения ключей.
4.
Открытое распределение ключей Диффи-Хеллмана и его модификации.
Протокол — это распределенный алгоритм, определяющий
последовательность действий каждой из сторон. В процессе выполнения протокола
идентификации каждая из сторон не передает никакой информации о своем секретном
ключе, а хранит его у себя и использует для формирования ответных сообщений на
запросы, поступающие при выполнении протокола. Наконец, применительно к самой
информации аутентификация означает проверку того, что информация, передаваемая
по каналу, является подлинной по содержанию, источнику, времени создания,
времени пересылки и т. д. Проверка подлинности содержания информации сводится,
по сути, к проверке ее неизменности (с момента создания) в процессе передачи
или хранения, то есть проверке целостности.
Аутентификация
источника данных означает подтверждение
того, что исходный документ был создан именно заявленным источником. Заметим,
что если стороны доверяют друг другу и обладают общим секретным ключом, то
аутентификацию сторон можно обеспечить применением кода аутентификации.
Действительно, каждое успешно декодированное получателем сообщение может быть
создано только отправителем, так как только он знает их общий секретный ключ.
Для не доверяющих друг другу сторон решение подобных задач с использованием
общего секретного ключа становится невозможным. Поэтому при аутентификации
источника данных нужен механизм цифровой подписи, который будет рассмотрен
ниже.
В целом,
аутентификация источника данных выполняет ту же роль, что и протокол
идентификации. Отличие заключается только в том, что в первом случае имеется
некоторая передаваемая информация, авторство которой требуется установить, а во
втором требуется просто установить сторону, с которой осуществляется
взаимодействие.
Создание цифровой подписи позволило решить проблему
сертификации открытых ключей. Она заключается в том, что перед тем как
использовать открытый ключ некоторого абонента для отправки ему
конфиденциального сообщения, отправитель должен быть уверен, что открытый ключ
действительно принадлежит этому абоненту. Открытые ключи необходимо очень
тщательно обезопасить, в том смысле, что если сервер, на котором они хранятся,
не обеспечивает их целостность и аутентичность, то злоумышленник имеет
возможность, подменив открытый ключ одного из абонентов, выступать от его
имени. Поэтому для защиты открытых ключей создаются специальные центры
сертификации, которые играют роль доверенной третьей стороны и заверяют
открытые ключи каждого из абонентов своими цифровыми подписями.
Сертификат представляет собой набор данных, заверенный
цифровой подписью центра и включающий открытый ключ и список дополнительных
атрибутов, принадлежащих абоненту. К таким атрибутам относятся: имена
пользователя и центра сертификации, номер сертификата, время действия
сертификата, предназначение открытого ключа (цифровая подпись, шифрование) и т.
д.
Международный стандарт ISO Х.509 определяет общую
структуру сертификатов открытых ключей и протоколы их использования для
аутентификации в распределенных системах.
Центры сертификации. Центр сертификации предназначен для регистрации абонентов,
изготовления сертификатов открытых ключей, хранения изготовленных сертификатов,
поддержания в актуальном состоянии справочника действующих сертификатов и
выпуска списка досрочно отозванных сертификатов. В некоторых системах функции
регистрации абонентов и обслуживания сертификатов разделяют, создавая
дополнительный центр регистрации (регистрационный центр).
Для сетей с большим числом абонентов создается
несколько центров сертификации. Центры сертификации, как правило, объединяются
в древовидную структуру, в корне которой находится главный центр сертификации,
который выдает сертификаты подчиненным ему отраслевым центрам, тем самым
обеспечивая доверие к открытым ключам этих центров. Каждый центр вышестоящего
уровня аналогичным образом делегирует право выпуска сертификатов подчиненным
ему центрам. В результате доверие сертификату открытого ключа каждого центра
основано на заверении его сертификата ключом вышестоящего центра. Сертификаты
главного центра подписывает сам главный центр.
Зная иерархию и подчиненность друг другу центров
сертификации, можно всегда точно установить, является ли абонент владельцем
данного открытого ключа. Основная трудность при создании центров сертификации
заключается в их юридическом статусе и потенциальных финансовых возможностях по
выплате компенсаций за ущерб, понесенный в результате невыполнения подписанных
цифровыми подписями с использованием сертификатов, выданных этим центром,
договоров и контрактов, сорванных по причине отказов от цифровых подписей или
их подделки.
Порядок использования криптографической системы
определяется системами установки и управления ключами.
Система установки ключей определяет алгоритмы и
процедуры генерации, распределения, передачи и проверки ключей.
Система управления ключами определяет порядок
использования, смены, хранения и архивирования, резервного копирования и
восстановления, замены или изъятия из обращения скомпрометированных, а также
уничтожения старых ключей.
Предварительное распределение ключей для надежной
защиты информации, передаваемой по открытому каналу связи, применяют
криптографические средства. Чтобы воспользоваться ими, необходимо осуществить
первоначальный выбор и установку ключей. Для генерации ключей могут применяться
различные алгоритмы. Выбранные ключи необходимо как-либо передать
взаимодействующим сторонам. Поэтому для первоначального распределения ключей
необходим защищенный канал связи.
Самый надежный способ первоначального распределения
ключей — это личная встреча всех взаимодействующих сторон. Можно использовать
также специальных курьеров, которые будут развозить ключи. Однако при большом
числе взаимодействующих сторон требуется предварительная рассылка значительного
объема ключевой информации и последующее ее хранение. Поэтому на практике
применяют специальные системы предварительного распределения ключей,
предусматривающие распределение и хранение не самих ключей, а некоторой меньшей
по объему исходной информации, на основе которой в дальнейшем каждая сторона
может вычислить ключ для взаимодействия с другой стороной.
Система предварительного распределения ключей включает
два алгоритма. С помощью первого алгоритма осуществляется генерация исходной
информации. Эта информация включает открытую часть, которая будет передана всем
сторонам или помещена на общедоступном сервере, а также секретные части каждой
стороны. Второй алгоритм предназначен для вычисления действующего значения
ключа для взаимодействия между абонентами по имеющейся у них секретной и общей
открытой части исходной ключевой информации.
Система предварительного распределения ключей должна
быть устойчивой, то есть учитывать возможность раскрытия части ключей при
компрометации, обмане или сговоре абонентов, и гибкой — допускать возможность
быстрого восстановления путем исключения скомпрометированных и подключения
новых абонентов.
Пересылка ключей. После того как предварительное распределение ключей произведено, может
потребоваться передача ключей для каждого конкретного сеанса взаимодействия.
Передача этих ключей может осуществляться с помощью шифрования с использованием
ранее полученных ключей.
Для передачи зашифрованных ключей по открытому каналу
связи между не доверяющими друг другу абонентами требуется решение всего
комплекса задач по установлению подлинности различных аспектов взаимодействия,
начиная от подлинности субъектов взаимодействия, подлинности пере даваемых
сообщений, подлинности самого сеанса связи и кончая подтверждением правильности
(идентичности) полученных абонентами ключей.
Для централизованного
управления пересылкой ключей создаются специальные доверенные центры,
выполняющие функции центров распределения или перешифрования ключей. Различие
между этими центрами заключается в том, что в первом случае генерация ключей
осуществляется в центре распределения, а во втором случае — самими абонентами.
Открытое
распределение ключей. Наиболее просто
распределение ключей осуществляется в системах открытого распределения (секретных)
ключей. Для сетей связи с большим числом абонентов традиционные подходы к
построению системы распределения ключей оказываются очень неудобными. Диффи и
Хеллман впервые показали, как можно решить эту задачу, используя незащищенный
канал связи.
В предложенной ими
системе открытого распределения ключей каждая из сторон изначально имеет свой
секретный параметр. Стороны реализуют определенный протокол взаимодействия по
открытому каналу связи. При этом они обмениваются некоторыми сообщениями
(образованными с помощью своих секретных параметров) и по результатам этого
обмена вычисляют общий секретный связной ключ. В более поздних работах такие
протоколы стали называть протоколами выработки общего ключа, поскольку
изначально ни одна из сторон не имеет ключа и как такового распределения или
пересылки ключей в нем не происходит.
В исходном виде
система Диффи и Хеллмана имела существенные недостатки, связанные с
возможностью для третьей стороны по осуществлению активного вхождения в канал
связи и проведению полного контроля передаваемой информации. Однако после
небольших модификаций и дополнений их протокол уже позволяет осуществлять не
только выработку общего ключа, но и одновременно проверять и подтверждать
правильность вычислений, а также проводить взаимную аутентификацию
взаимодействующих сторон.
Схема разделения секрета.
Еще одной задачей
современной криптографии, тесно связанной с проблемой распределения ключей и
активно развивающейся в последние годы, является задача построения схем
разделения секрета. Для многих практически важных приложений, связанных с
запуском или активизацией критических процессов или определяющих порядок
получения доступа к значимым данным, ответственное лицо должно ввести секретный
ключ. Чтобы обезопасить процедуру принятия решения и не отдавать все на волю
одного человека, являющегося обладателем ключа, используют метод разделения
секрета.
Он состоит в
назначении определенной группы лиц, которая имеет право принимать решение.
Каждый член группы владеет определенной долей секрета (точнее, специально
выбранным набором данных), полная совокупность которых позволяет восстановить
секретный ключ. При этом схема разделения секрета выбирается с таким условием,
что для восстановления секретного ключа требуется обязательное присутствие всех
членов группы, так как в случае отсутствия хотя бы одного из участников
объединение долей оставшихся членов группы гарантированно не позволяет получить
никакой информации о секретном ключе. Таким образом, схема разделения
секрета определяется двумя алгоритмами, удовлетворяющими сформулированному
выше условию: первый алгоритм определяет порядок вычисления значений долей по
заданному значению секретного ключа, а второй предназначен для восстановления
значения секрета по известным долям.
Задачу построения
схемы разделения секрета можно обобщить:
- либо путем введения так
называемой структуры доступа, когда решение может приниматься не одной,
а несколькими различными группами, причем часть из участников может наделяться
правом "вето";
- либо путем добавления
механизмов, позволяющих обнаружить обман или сговор участников;
- либо введением
специального протокола распределения долей между участниками с подтверждением
правильности полученной информации и аутентификацией сторон.
Диффи
и Хелман предложили для создания криптографических систем с открытым ключом функцию дискретного возведения в степень.
Необратимость
преобразования в этом случае обеспечивается тем, что достаточно легко вычислить
показательную функцию в конечном поле Галуа состоящим из p элементов. (p - либо
простое число, либо простое в любой степени). Вычисление же логарифмов в таких
полях - значительно более трудоемкая операция.
Если y=ax,, 1<x<p-1, где - фиксированный элемент поля GF(p), то x=loga
y над GF(p). Имея x, легко вычислить y.
Для этого потребуется 2 ln(x+y) операций умножения.
Обратная
задача вычисления x из y будет достаточно сложной. Если p выбрано достаточно правильно, то
извлечение логарифма потребует вычислений, пропорциональных:
L(p) = exp { (ln p ln ln p)0.5 }
Для
обмена информацией первый пользователь выбирает случайное число x1, равновероятное из целых
1...p-1. Это число он держит в
секрете, а другому пользователю посылает число:
y1 = ax mod p
Аналогично
поступает и второй пользователь, генерируя
x2 и вычислив y2,
отправляя его первому пользователю. В результате этого они могут вычислять k12 = ax1x2 mod p.
Для
того, чтобы вычислить k12,
первый пользователь возводит y2
в степень x1. То же делает
и второй пользователь. Таким образом, у обоих пользователей оказывается общий
ключ k12, который можно
использовать для шифрования информации обычными алгоритмами. В отличие от
алгоритма RSA, данный алгоритм не позволяет шифровать собственно информацию.
Не
зная x1 и
x2, злоумышленник может попытаться вычислить k12, зная только
перехваченные y1 и
y2. Эквивалентность этой проблемы проблеме вычисления
дискретного логарифма есть главный и открытый вопрос в системах с открытым
ключом. Простого решения до настоящего времени не найдено. Так, если для
прямого преобразования 1000-битных простых чисел требуется 2000 операций, то
для обратного преобразования (вычисления логарифма в поле Галуа) - потребуется
около 1030 операций.
Как
видно, при всей простоте алгоритма Диффи-Хелмана, вторым его недостатком по
сравнению с системой RSA является отсутствие гарантированной нижней оценки
трудоемкости раскрытия ключа.
Кроме
того, хотя описанный алгоритм позволяет обойти проблему скрытой передачи ключа,
необходимость аутентификации остается. Без дополнительных средств, один из
пользователей не может быть уверен, что он обменялся ключами именно с тем
пользователем, который ему нужен. Опасность имитации в этом случае остается.
1.
А.П.Алферов, А.Ю.Зубов, А.С.Кузьмин, А.В.Черемушкин. Основы криптографии:
Учебное пособие. – М.: Гелиос АРВ, 2005. стр. 78-88.
2.
В.М. Фомичев. Дискретная математика и криптология Курс лекций. – М.:
ДИАЛОГ-МИФИ, 2003. стр. 161-174.
3.
Шаньгин В.Ф. Защита компьютерной информации. Эффективные методы и средства. –
М.: ДМК Пресс, 2008. стр. 171-185.
Атака - это реализация угрозы безопасности для криптосистемы.
Аутентификация - процесс проверки соответствия полученной информации
заявленной. Различают аутентификацию данных, источника данных и опознавание
участника протокола.
Гаммирование – процесс наложения по определенному закону гаммы шифра на
открытые данные. Под гаммой шифра понимается псевдослучайная двоичная
последовательность, вырабатываемая по заданному алгоритму и предназначенная как
для зашифрования открытых данных, так и для расшифрования.
Дешифрование – это нарушение конфиденциальности шифртекста, достигнутое
методами криптоанализа.
Достоверность – свойство информации, выражающееся в строгой
принадлежности объекту, который является её источником, либо тому объекту, от
которого эта информация принята.
Зашифрование – процесс маскировки сообщения способом позволяющим скрыть
его суть.
Имитозащита является частным случаем аутентификации. Если
криптоалгоритм обеспечивает защиту получателя от навязывания ложной информации,
то говорят, что криптоалгоритм реализует имитозащиту данных.
Ключ – это сменный элемент шифра, применяемый для зашифрования
отдельного сообщения, обеспечивающий выбор одного варианта преобразования из
совокупности возможных. Ключом определяется в первую очередь криптостойкость
защищаемой информации. Множество возможных ключей называют пространством
ключей.
Коллизией называется пара аргументов М и М, которым
соответствует одно и то же значение хэш-функции: h(M)
= h(М’).
Если число таких аргументов равно n, то говорят о коллизии кратности n. Если хэш-функция не имеет коллизий при заданных
ограничениях на длину аргумента, то она называется свободной от коллизий.
Конфиденциальность – свойство
информации быть доступной только ограниченному кругу пользователей
информационной системы, в которой циркулирует данная информация.
Криптоанализ – это раздел прикладной математики изучающий методы,
алгоритмы, программные и аппараты средства анализа криптосистем с целью
извлечения конфиденциальных данных.
Криптографический протокол – алгоритм, выполняемый не менее чем двумя сторонами,
задаваемый последовательностью операций, выполняемых каждой из сторон.
Криптография – это раздел прикладной математики изучающий методы
преобразования информации в целях сокрытия ее содержания.
Криптосистема – это система, реализованная программно, аппаратно или программно - аппаратно и осуществляющая
криптографическое преобразование информации. Она состоит из пространства
ключей, открытых текстов, шифртекстов и алгоритмов зашифрования и
расшифрования.
Оперативность – способность информации или некоторого информационного
ресурса быть доступным для конечного пользователя в соответствии с его
временными потребностями.
Открытый текст – исходное сообщение.
Отправитель – это субъект, посылающий сообщение.
Получатель – это субъект, получающий данное сообщение.
Расшифрование – процесс
преобразования шифртекста в открытый текст.
Синхропосылка – исходные открытые параметры алгоритма криптографического
преобразования.
Стеганография применяется для скрытия факта передачи секретных сообщений
в другие сообщения, при этом скрывается даже само существование секрета.
Стойкость криптоалгоритма (криптостойкость) заключается в способности шифра
противостоять попыткам его расшифрования. Криптостойкость зависит от сложности
алгоритма преобразования, длины ключа и объема ключевого пространства.
Текст – упорядоченный набор из элементов выбранного алфавита.
Хэш-функция – это функция, отображающая аргумент произвольной конечной
длины в образ фиксированной длины. Функция, для которой по данному аргументу
вычислить её значение легко, а по данному значению функции аргумент найти
сложно, называется хэш-функцией, вычислимой в одну сторону. Все хэш-функции
считаются вычислимыми в одну сторону. Если хэш-функция зависит от
секретного ключа, она называется ключевой, в противном случае – бесключевой.
Целостность – свойство информации или программного обеспечения
сохранять свою структуру и содержание в процессе передачи и хранения.
Шифр – совокупность обратимых преобразований множеств открытых
данных на множество зашифрованных данных, заданны алгоритмом криптографического
преобразования.
Шифртекстом (криптограммой) называется зашифрованное сообщение.
ID:1029110